基于动力触探的高速铁路路基压实状态分析
2020-09-27芦巍
芦巍
(中铁二十一局集团第四工程有限公司,西安 710065)
高速铁路路基变形与压实标准高,压实状态主要通过压实系数K、动态变形模量Evd、地基系数K30等指标予以评判。对于海外中断建设的高速铁路路基工程,压实指标只能在路基施工面层测试。DPT(Dynamic Penetration Test,动力触探)是岩土工程勘察中一种重要的原位测试手段,近年来在地基承载力与变形参数测算、填土密实度检测等领域的应用已较为广泛。王祎望等[1]通过载荷试验与DPT对比,建立了地基承载力标准值与DPT 锤击数的经验关系,并在建筑物强夯地基处理工程中得到应用;Shahien 等[2]开展了砾石土平板载荷试验与DPT 测试,建立了考虑颗粒尺寸大小的变形模量计算公式,并采用现场实测沉降数据予以修正;温世亿等[3]基于可变能量动力触探仪所测锥尖阻力与压实度的相关性,提出了一种渠道填筑工程压实度快速检测方法;陈春东等[4]为克服常规检测方法的局限性,通过对比试验探究DPT锤击数与压实度的关系,提出了一种DPT检测机场填土密实度的方法。
DPT尚未应用于评价已填高速铁路路基压实状态,为适应海外中断建设的高速铁路路基压实检测评估需要,结合一国外高速铁路建设工程,选取典型试验段开展分层开挖分层原位试验,建立压实指标模型预测方法。
1 原位测试概况
国外一高速铁路全长246 km,路基比例达97%,已采用UIC 标准按时速250 km 有砟轨道铁路进行施工图设计,并完成70%线下土建工程,大部分路基工程已填至基床底层顶面。现拟采用中国标准、按时速300 km 无砟轨道铁路进行施工图整改设计,须对已建路基工程进行检测评估,其中路基压实状态评价是重点之一。
在现场选取A,B,C,D,E 共5个试验段,填料总体均质。每一测试层面上设置5 个测试区,如图1 所示,图中L为路基施工顶面宽度。
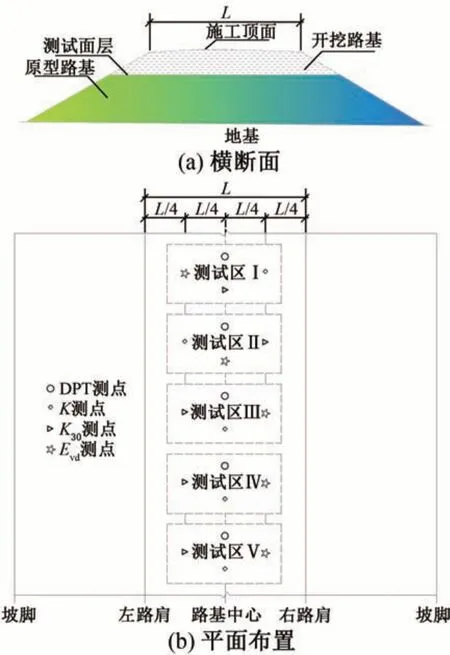
图1 原位测试方案
原位测试具体实施步骤如下:①参照图1(b)测点布置,在已填路基顶面开展压实指标及DPT 原位测试。②分层开挖路堤,开挖厚度为100 ± 10 cm,整平各层开挖面后重复步骤①直至路基基底。
2 压实模型建立
文献[5]基于现场对比试验及室内模拟试验,建立了粉煤灰压实系数K与锤击数N10的关系式:

式中,N10为10 kg 重锤击入10 cm 所用锤击数,其应用前提是当N10>25击时按25击计数。
文献[6]通过环刀法试验与击实试验,建立了路堤压实系数K与锤击数N10的回归方程:

式(1)和式(2)可用于预测路基压实系数K,但K随N10的增加不断增大,难以收敛,与实际工程状态不吻合。文献[6]作出当N10>25 击时按 25 击计数的限定,但以25击作为分界条件尚缺乏充分的论证依据。
为研究压实指标与DPT 锤击数N63.5的关系,以f(N63.5)代表压实指标K,Evd,K30任意一项,其具有以下特征。
1)f(N63.5)均随N63.5的增加而不断增大,即f(N63.5)增长率大于等于0,可表示为
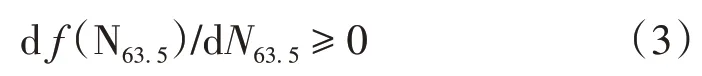
2)随着路基填料压实度不断增大,土体压密程度变大,孔隙率降低,压密难度增大,从而导致f(N63.5)增长率越来越慢。可表示为

当填料逐渐趋于完全压密状态时,填料压实指标f(N63.5)也将趋于某一定值。
根据以上特点,建立压实指标f(N63.5)与N63.5的模型关系:

式中:F,Q,p为模型参数;p为定值,单位为 10 cm/击,反映了f(N63.5)随N63.5的变化率,可由室内模型试验或现场试验确定。
当N63.5→0时

当N63.5→∞时

对式(5)求一阶和二阶导数得
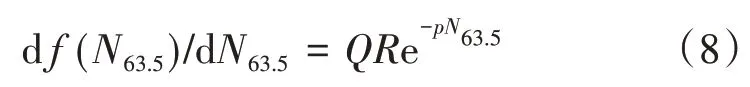

由 于F>f0,则Q>0。 若 df(N63.5)/dN63.5≥0 且则参数p必须满足p≥0。
3 模型验证及精度分析
为验证DPT 分析模型式(5)的可行性,取A,B 试验段测取的压实指标及N63.5(共计100 组数据)确定参数F,Q,p,再以C,D,E 试验段测得的压实指标及N63.5(共计140组数据)分析模型预测精度。本文DPT分析模型适于分析路基面以下0.2 m的压实指标。
3.1 模型参数
用式(5)拟合图2 中测试数据,确定模型参数,见表1。K与N63.5之间相关性最高,其次分别为K30与N63.5,Evd与N63.5。

图2 现场测试数据拟合结果

表1 模型参数
3.2 精度分析
根据上述DPT 分析模型预测C,D,E 试验段压实指标并与实测值对比,见图3。可知,模型预测值与实测值吻合得较好。
为进一步量化模型的预测能力,定义均方根误差(Root Mean Square Error)[7]ERMSE为

式中:i为数据点编号;n为测点总数目;Fm(i)为压实指标f(N63.5)实测值;Fp(i,N63.5)为N63.5取某一测试值时对应的压实指标f(N63.5)模型预测值。

图3 压实指标预测结果
表 2 列出了 DPT 分析模型对上述f(N63.5)均方根误差值,可见Evd的最大,其次为K30,K最小。由此可见,DPT 分析模型对K预测效果最好,其次分别为K30和Evd。

表2 模型计算均根误差值
3.3 模型修正

图4 模型预测值与实测值的关系
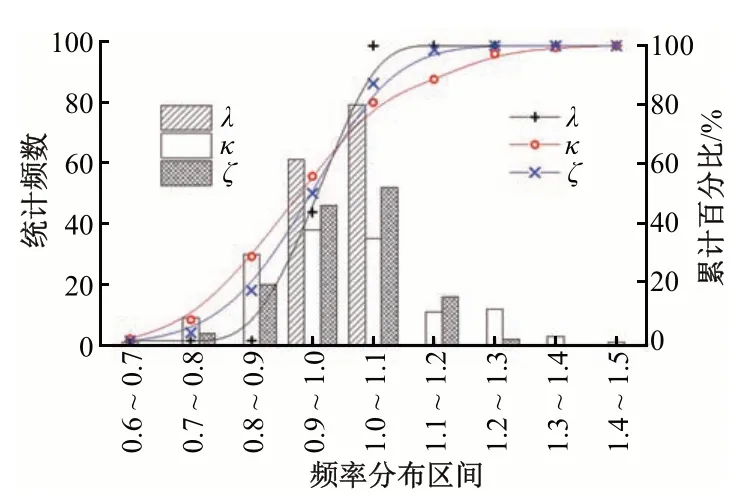
图5 λ,κ和ζ频率分布

式中:α取值0.960~1.030;β取值0.970~1.020。

表3 λ,κ和ζ统计
4 结论
1)路基压实指标均随DPT 锤击数N63.5增加而不断增大,由于土体压密程度变大、孔隙率降低等原因导致压实指标随N63.5增长率越来越慢,当路基填料逐渐趋于完全压密状态时,压实指标也将趋于某一定值。
2)根据压实指标与N63.5关系曲线特征,建立了路基压实指标DPT 分析模型。数据拟合表明,在DPT 分析模型中,K与N63.5之间相关性最高,其次为K30与N63.5和Evd与N63.5。
3)结合现场试验段实测数据,分析了DPT 分析模型的预测能力,认为DPT 分析模型对K的预测精度最高(均方根误差为0.011 8),其次分别为K30和Evd。
4)基于DPT 分析模型修正系数统计,提出了具有95%可靠度的K与N63.5,Evd与N63.5,K30与N63.5统计修正模型。
本文研究成果在国外一高速铁路应用后,大幅节约了工程投资。
