基于Fuzzy-DBN的氨泄漏爆炸事故风险分析
2020-09-27许开立陈守坤徐晓虎
程 洁,许开立,陈守坤,徐晓虎
(东北大学资源与土木学院,辽宁 沈阳 110819)
随着生活品质的提高,人们对制冷技术的需求日益增加,制冷技术在生活中的应用十分广泛,尤其在食品生产、化工生产、大型超市、冷库等行业的应用最为突出。由于国家对企业排放的污染物有严格的限制要求,越来越多的企业选用氨这一经济、高效、环保的制冷剂,可将臭氧耗损潜能值(ODP)、全球变暖潜能值(GWP)控制为零。由于氨制冷剂具有良好的热力学性能和对大气层无任何不良效应,且价格低廉,已在全球约80%的大型冷库中得到应用[1]。但关于氨制冷剂生产、使用、储存等相关法规及规范性文件未能随氨制冷技术的发展情况和氨制冷事故的经验教训及时做出相应的调整和改进,导致氨制冷系统安全事故频繁发生。根据《危险化学品目录》(2018年版),氨(液氨)为危险化学品,火灾危险性为乙类,为国家安监总局发布的首批重点监控的危险化学品,是第一批60种重点监控的危险化学品之一,一旦发生氨泄漏,可能引起中毒、爆炸或火灾等事故,对人员健康、企业经济以及周边环境均会造成严重的影响。目前,氨泄漏导致的中毒事故较为多发,许多学者对氨气泄漏可能造成的人员中毒或冻伤等事故建立了事故应急处置方案并进行了研究,如罗振敏等[2]、柳红卫等[3]、李海航等[4]对氨泄漏扩散导致中毒及环境污染的风险进行了研究;孟凡亭等[5]利用事故树和模糊集理论方法对氨泄漏爆炸事故进行了分析;Kang等[6]对氨系统储罐进行了风险分析,并对氨气泄漏事故频率进行研究;Chen等[7]根据往年氨泄漏事故的统计分析,研究了氨泄漏发生的原因和氨扩散的影响因素。2013年6月3日,吉林省德惠市的吉林宝源丰禽业有限公司电气线路短路引发火灾,造成物理爆炸,使氨制冷系统高压管路发生泄漏导致厂区氨气弥漫,浓度达到爆炸极限,工人受到吸入性窒息气体与爆炸冲击波的伤害,最终造成121人死亡、76人受伤[8]。由此可见,氨泄漏发生爆炸事故导致的后果及其严重,故为了有效控制氨泄漏爆炸事故,对氨泄漏爆炸事故的风险进行研究就显得尤为必要。为此,本文提出将动态贝叶斯网络模型与模糊数学方法相结合的思路,以氨制冷系统为例,针对氨泄漏爆炸事故进行了风险分析。
1 动态贝叶斯网络
传统的事故树、故障树和静态贝叶斯网络模型在分析复杂系统多阶段、组件多态、事件相关等特性时往往有较大的局限性,而动态贝叶斯网络可以以局部状态和条件概率的形式描述系统的状态空间、失效相关性和动态演化过程,是贝叶斯网络在时间维度上进行信息融合而形成的具有双向信息推理能力的安全风险数学建模方法[9],它在马尔可夫模型的基础上,融合了上一时间片的状态间转移概率,依次将信息传递到下一时间片。
动态贝叶斯网络涉及的“动态”并非模型框架随时间发生改变,一般的动态贝叶斯网络的拓扑网络在各时间片内是相同的,然而各节点条件概率结合观测值及推理算法随时间发生变化。为了方便对氨制冷系统氨泄漏爆炸事故进行风险评估,对动态贝叶斯网络做如下假设和处理:
(1) 随机过程满足马尔可夫性。
(2) 在有限时间内,相邻的随机过程稳定。即对于任意的t时刻,条件概率P(Xt|Xt-1)都是相同的,为一个独立于时间的常量。
基于上述假设,建立在时间轨迹上的动态贝叶斯网络,对于任意时刻t,X1,X2,…,Xt+1联合概率分布为
(1)
式中:PB0为初始状态概率分布;PB→为t时刻到t+1时刻的转移概率分布,反映相邻时间片之间的因果逻辑关系。
利用动态贝叶斯网络进行前向推理,即预测推理(Forward Reasoning 或 Predictive Reasoning),从先验概率开始的正向推理过程,用于计算事故后果状态的概率分布,支持安全预警或风险信息的辅助决策。将变量Xj的状态k的概率分布、变量[X1,X2,…,Xj-1,Xj+1,…Xn]的状态作为证据融入贝叶斯网络模型[9],有:
(2)
式中:pa(xi)表示xi的所有父节点。
目前,大量研究表明用于风险评估的动态贝叶斯方法仅基于多组静态数据的结果,少数动态评估方法基于定期对有限个节点的观测[10]。其次,如何确定各节点条件概率是研究贝叶斯网络推理最关键的问题,若其父节点数量过多时,则条件概率表中各状态组合结果呈指数增长型,对推理造成一定程度的困难。另外,将动态贝叶斯网络模型方法应用于一些实际问题时,由于实际可获得的统计数据较少,或观测困难等现实因素的限制,无法做到实时的数据输入进行动态贝叶斯网络推理,因此通过专家经验给出一些节点的条件概率。一般地,在进行专家意见询问时,专家们通常会给出一些模糊的语言描述来表示某一事件发生的可能性(例如:三值判断即最低、可能、最高;模糊语言描述;区间判断等),将具体给出的专家意见语言描述转化为三角模糊数或梯形模糊数[11],则能处理一些多状态、多节点的条件概率问题。由于在较短一段时间内氨制冷系统发生氨泄漏爆炸事故的概率极低,现实可获取的数据较为有限,因此本文将专家经验知识与模糊数学理论相结合作为一种不确定性的推理方法来确定动态贝叶斯网络中的条件概率,并利用动态贝叶斯网络推理功能对制冷站或冷库中氨制冷系统氨泄漏爆炸事故构建模糊动态贝叶斯网络风险评估模型。
2 基于Fuzzy-DBN建立氨泄漏爆炸事故风险评估模型
本文根据文献[12]所建立的故障树,通过逻辑及条件相关因素,将故障树转化为动态贝叶斯网络拓扑图,具体转化方法如图1所示。其中,故障树中的底事件、中间事件、顶事件分别对应着贝叶斯网络的根节点、中间节点、叶节点; 故障树中底事件的发生概率对应着贝叶斯网络根节点发生的先验概率;故障树中的逻辑门由条件概率表(CPT)表示。在动态贝叶斯网络中,最关键的要素为条件概率参数的确定,本文将模糊数学方法应用到动态贝叶斯网络中。
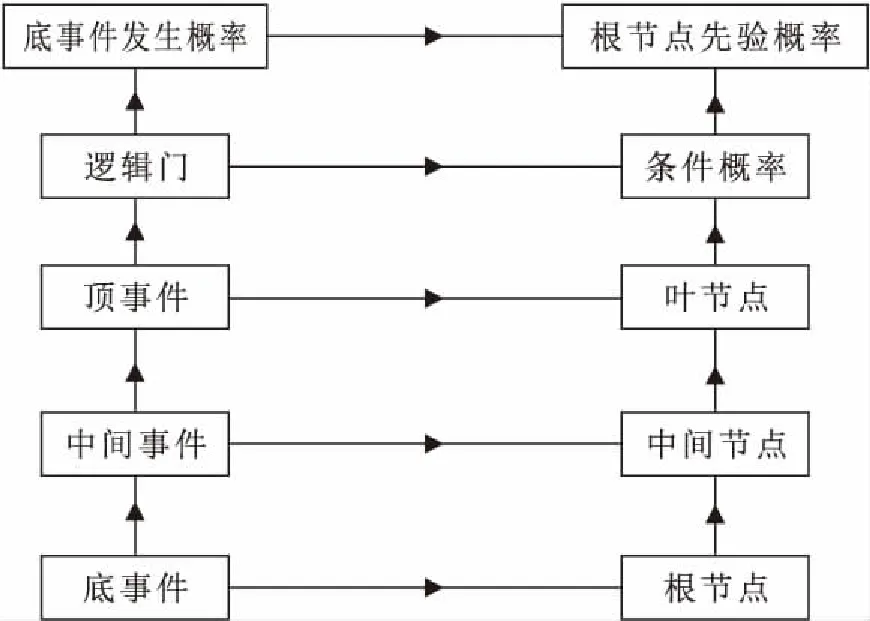
图1 故障树转化为动态贝叶斯网络的规则逻辑图Fig.1 Regular logic diagram for transforming a fault tree into a dynamic Bayesian network
根据上述转化规则,利用GENIE软件建立了氨制冷系统氨泄漏爆炸事故风险评估的模糊动态贝叶斯网络模型,见图2。贝叶斯网络各根节点发生的先验概率见表1。
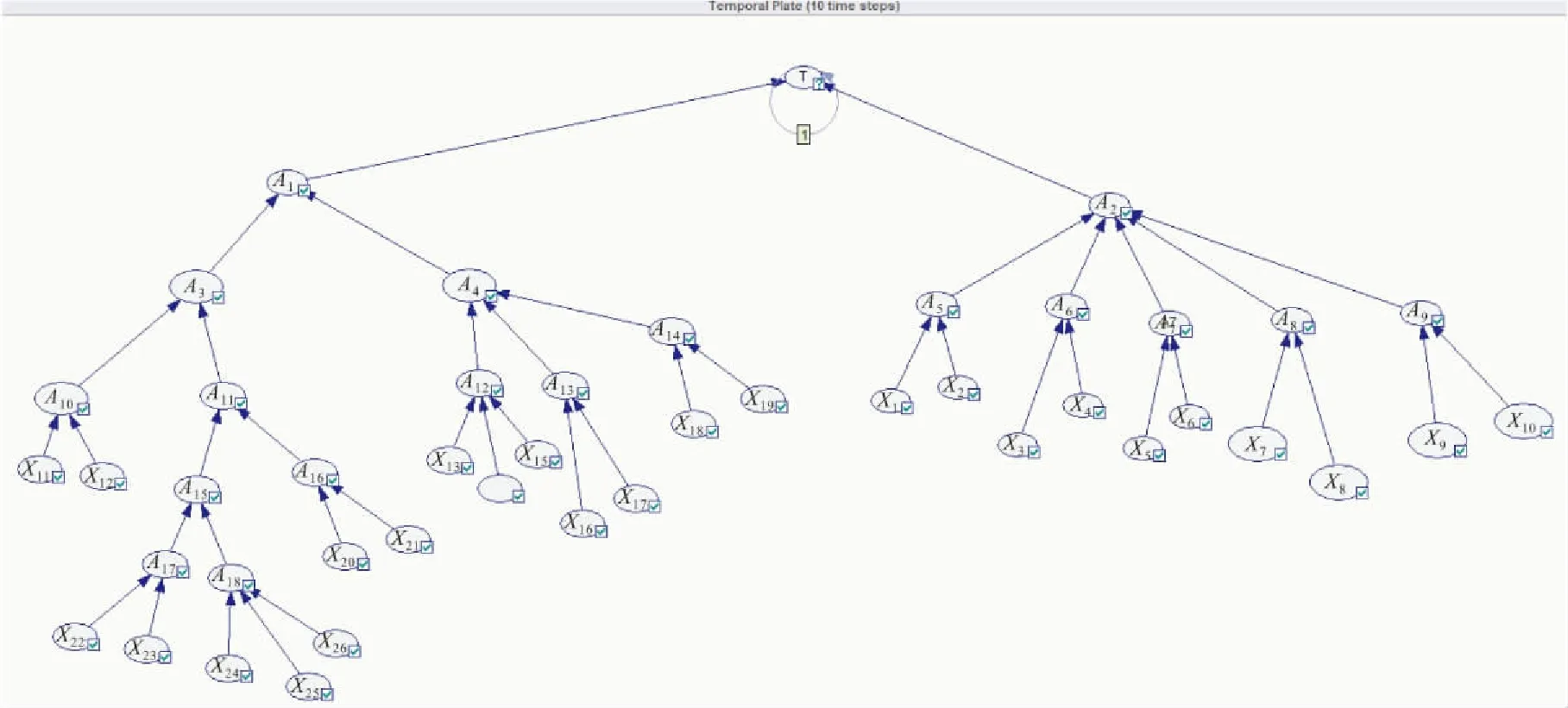
图2 氨制冷系统氨泄漏爆炸事故风险评估的模糊动态贝叶斯网络(Fuzzy-DBN)模型 Fig.2 Fuzzy-DBN model for the risk assessment of ammonia leakage explosion accidents in ammonia refrigeration system
对上述所建立的动态贝叶斯网络做进一步分析,中间事件的条件概率采用专家打分的模糊数学方法确定。以储罐破坏为例,储罐破坏是由于开关阀门破坏或罐体腐蚀损坏导致的,开关阀门破坏、罐体腐蚀损坏均有2种状态,分别为发生(present)、不发生(absent)。
风险评价等级是对概率风险评价中某事件发生概率的判断,是风险的语言描述集合。若风险评价等级的划分过于宽泛,则无法准确地对风险进行评估;若风险等级划分过于密集,则会对风险描述造成困难。因此,对于同一种客观情况,不同的人根据其自身理解有不同的划分类型[11]。本文采用模糊评价中的模糊数(fuzzy number)来对这些模糊的语言描述进行量化表示,采用的专家意见语言集为“很低、低、较低、中等、较高、高、很高”7个等级的语言描述,再利用三角模糊数(triangular fuzzy number)和梯形模糊数(trapezoidal fuzzy number)对专家语句进行转化[12]。常见的三角模糊数和梯形模糊数分别表示为(a,b,c)和(a,b,c,d),λ截集已由文献[13]得到推理证明。发生概率语言描述对应的模糊数形式和λ截集见表2,其中“VL、L、FL、M、FH、H、VH”分别代表“很低、低、较低、中等、较高、高、很高”。
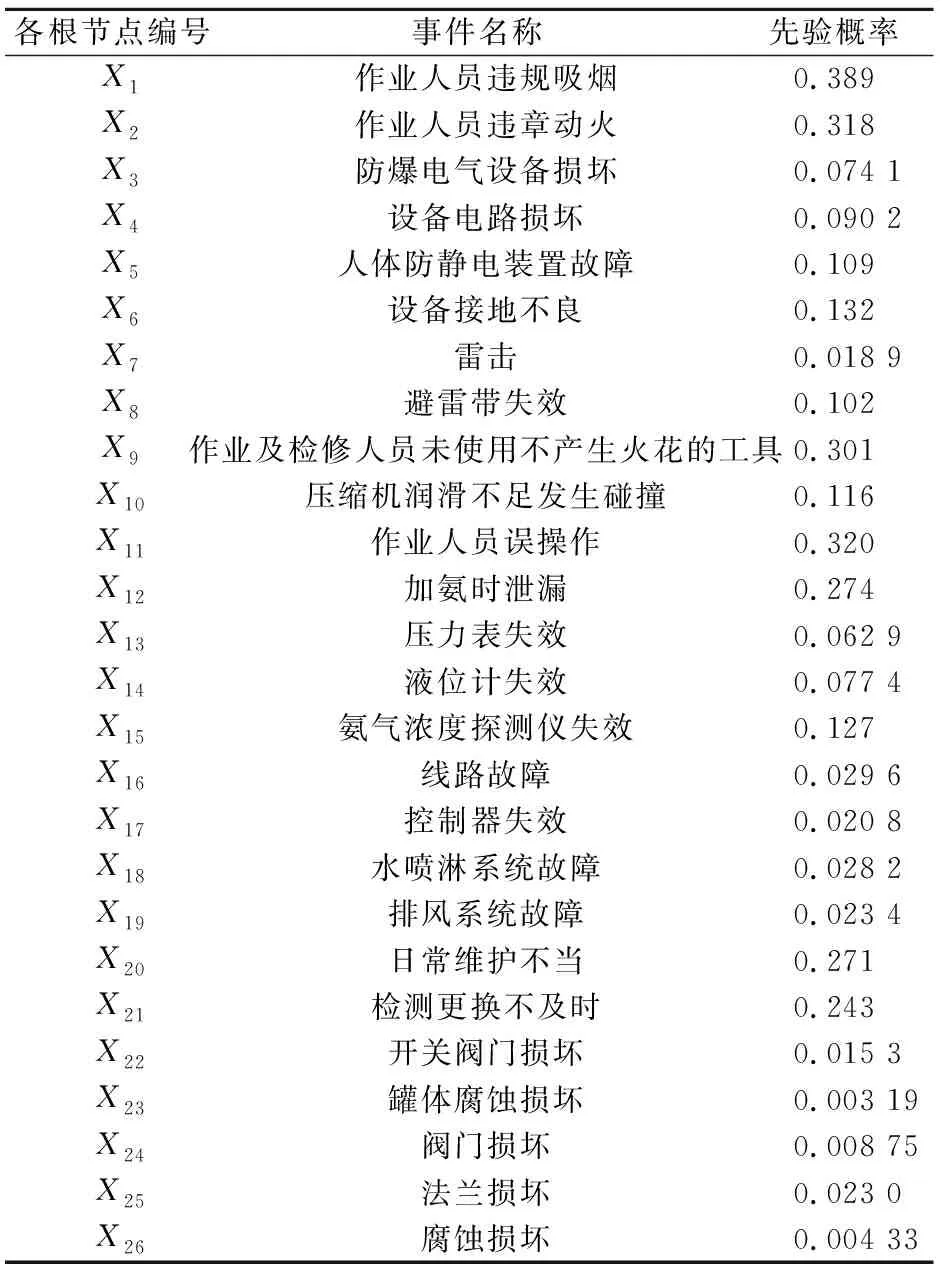
表1 贝叶斯网络各根节点发生的先验概率表

表2 发生概率语言描述对应的模糊数形式和λ截集
以“人失误”节点为例,3位专家对人失误要素各底事件不同状态下的模糊语言评价集,见表3。

表3 三位专家对人失误要素的模糊语言评价集
序列1中,当X11、X12处于都不发生的状态时,计算A10不发生的条件概率。序列1的平均模糊数为
=[0.1λ+0.767,-0.033λ+0.967]
(3)
式中:I1表示序列1的平均模糊数;f1、f2、f3表示3位专家语言描述对应的模糊数形式。
由于各影响因素的状态集合都是模糊分类的结果,而输入模型的数据为似然概率,因此采用隶属函数来进行语言集与似然概率之间的转换[14],并利用积分法求解模糊数,具体如下:
(4)
(5)
I1=αμR(I1)+(1-α)μL(I1)=0.930 6
(6)
式中:μL(I1)表示模糊数左隶属函数反函数的积分值;μR(I1)表示模糊数右隶属函数反函数的积分值;nλ、mλ分别表述模糊数I1的λ截集的上、下界,λ=0,0.1,0.2,…,1;Δλ=0.1;α∈[0,1]为乐观指数,取决于决策者针对转换结果的态度,α=0、α=1分别表示解模糊结果的上、下界[15]。
因此,事件X11、X12都不发生的情况下,经专家判断与模糊数计算,得到“人失误”不发生的概率为0.930 6,则“人失误”发生的概率为0.069 4。
依据此方法,可得到各个中间节点的条件概率,即应急失效节点的条件概率表CPT(Conditional Probability Table),以及顶事件的状态转移概率即在初始时刻的某一状态转移到下一时刻的状态的概率,其页面显示见图3和图4。

图3 应急失效节点的条件概率页面显示Fig.3 Conditional probability page display of emergency failure node

图4 顶事件的状态转移概率页面显示Fig.4 Top event state transition probability page display
3 基于Fuzzy-DBN的氨泄漏爆炸事故基本事件概率分析
基于氨泄漏爆炸事故风险评估的动态贝叶斯网络模型分析结果,最终推理出10个时间片内顶事件发生的概率,其页面显示见图5。其中,第一行为10个时间片内氨泄漏爆炸事故发生的概率,第二行为10个时间片内氨泄漏爆炸事故不发生的概率。利用GENIE软件导出氨泄漏爆炸事故贝叶斯网络各根节点的后验概率,见表4。

图5 10个时间片内顶事件发生的概率页面显示图Fig.5 Probability of top event occurrence in 10 time slices

表4 贝叶斯网络各根节点的后验概率
由表4可知,各根节点(基本事件)发生的后验概率排序如下:X1>X11>X2>X9>X12>X20>X21>X6>X15>X10>X5>X8>X4>X14>X3>X13>X16>X18>X19>X25>X17>X7>X22>X24>X26>X23。
从氨泄漏爆炸事故基本事件发生的后验概率排序结果可知:作业人员违规吸烟X1、作业人员违章动火X2、作业及检维修人员未使用不产生火花的工具X9是导致氨泄漏爆炸事故的主要火源形式,氨制冷企业应重点加以防控;作业人员误操作X11是导致氨制冷系统氨泄漏的重要原因,加氨时泄漏X12、日常维护不当X20、检测更换不及时X21是导致氨制冷系统氨泄漏的突出问题,氨制冷企业应从防控这四个因素方面优先采取控制措施。
4 基于Fuzzy-DBN的氨泄漏爆炸事故发生概率预测
假设将A3(氨泄漏报警)节点设置为证据节点,证据输入见图6,通过核查氨制冷系统氨泄漏报警记录,从初始时间片到第5个时间片均未发生氨泄漏报警,但在第6个时间片时发生氨泄漏报警,氨制冷车间对泄漏源及时采取了有效控制措施后,预测氨制冷系统再次发生氨泄漏爆炸事故的概率,见图6和图7。
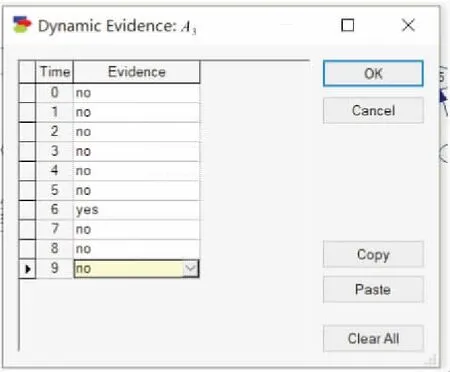
图6 氨泄漏报警节点的证据输入页面显示图Fig.6 Evidence input for liquid ammonia leakage alarm nodes
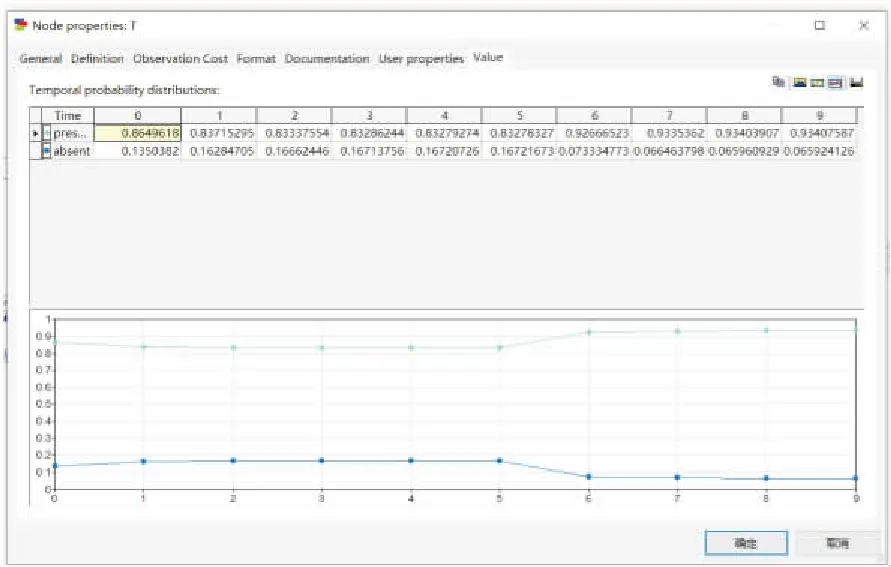
图7 输入氨泄漏报警节点证据后顶事件发生的 概率页面显示图Fig.7 Probability of top event after inputting liquid ammonia leakage alarm node evidence
由图7可见,未发生过泄漏报警的氨制冷系统,发生氨泄漏爆炸事故的概率约为0.83,曾经发生过泄漏报警的氨制冷系统,发生氨泄漏爆炸事故的概率约为0.93,说明发生过泄漏报警的氨制冷系统比未发生过氨泄漏报警的氨制冷系统发生氨泄漏爆炸事故的可能性更大。
5 氨制冷系统预防氨泄漏爆炸事故风险的控制措施
基于Fuzzy-DBN的分析计算结果,本文建议氨制冷企业应采取以下关键控制措施,以防控氨泄漏爆炸事故的风险:
(1) 氨制冷企业应加强对火源的日常管理,严禁在厂区内吸烟。
(2) 在设备选用上,采用本质安全高的制冷设备,或采取防止人失误措施,确保即使在人员发生误操作的情况下,设备也不发生故障。
(3) 氨制冷企业应加强对本单位及相关方现场作业的安全管理,严格审查作业许可,并加强现场危险作业的监管。
(4) 氨制冷系统检维修作业及应急处置过程应全部采用不发生火花的工具,避免在检维修作业或应急堵漏中产生撞击火花;而针对制冷设备的运行电机应选用防爆型。
(5) 氨制冷企业在进行加氨操作前,应严格核查加氨槽车、押运员及驾驶员等相关资质,并在加氨站附近应配备足够数量的应急救援物资和工具,厂区相应区域应拉线警戒,同时严格要求相关人员在加氨操作时遵循加氨操作规程。
6 结 论
本文基于模糊动态贝叶斯网络(Fuzzy-DBN)方法对氨制冷系统氨泄漏爆炸事故进行了风险研究,得出以下结论:
(1) 根据氨泄漏爆炸事故故障树,利用GENIE软件建立了氨泄漏爆炸事故风险评估的模糊动态贝叶斯网络模型。
(2) 利用建立的氨泄漏爆炸事故风险评估的模糊动态贝叶斯网络模型,计算氨泄漏爆炸事故基本事件发生的先验概率,得出导致氨泄漏爆炸事故发生的关键火源因素及泄漏因素。
(3) 基于动态贝叶斯网络,根据氨制冷系统发生氨泄漏报警情况,对氨泄漏爆炸事故发生概率进行预测,结果表明:发生过泄漏报警的氨制冷系统比未发生过氨泄漏报警的氨制冷系统发生氨泄漏爆炸事故的可能性更大。
(4) 基于贝叶斯网络分析计算出的氨泄漏爆炸事故基本事件发生的后验概率的排序结果,提出了预防氨泄漏爆炸事故应优先采取的控制措施。
