基于EW-AHP和未确知测度理论的隧道坍塌风险评价
2020-09-27顾伟红
翟 强,顾伟红
(兰州交通大学土木工程学院,甘肃 兰州 730070)
隧道施工地下工程项目与其他工程项目相比,具有隐蔽性、复杂性、不确定性和安全隐患大等突出的特点,因此隧道工程施工过程中安全事故屡屡发生。塌方作为岩石隧道施工中最常见的灾害,主要是由于受不良地质断裂破碎带、地下水等影响使岩石失去控制而导致的。隧道坍塌不仅会给隧道施工带来巨大的困难,而且还会使施工成本、时间和意外事故发生的可能性增加,因此预测隧道坍塌风险的可能性已成为隧道研究的热点问题。
近些年,许多学者对隧道坍塌风险进行了评估。如张晨曦等[1]运用层次分析法与多层次模糊综合决策法确定了山岭隧道施工中塌方风险事件的可能性等级;朱捷等[2]通过文献总结和现场调查,统计了大量的隧道坍塌工程案例,对引起隧道坍塌的风险源进行了辨识与分析,对构建隧道坍塌风险评价体系起着至关重要的作用;亓晓贵等[3]和于咏妍[4]基于模糊层次分析方法对隧道坍塌风险进行了评估;周建昆等[5]采用概率分析事故树理论对隧道塌方事故进行了预测;孙彦峰[6]选取岩石单轴饱和抗压强度等12个影响因素建立隧道塌方风险评价体系,并基于理想点法对隧道塌方风险进行了评价;杨光等[7]和时惠黎等[8]为了解决隧道塌方事故的复杂性和模糊性问题,运用云模型对隧道塌方风险等级进行了评价;苏永华等[9]针对传统的模糊综合评价中评价指标权重的确定过分依赖专家经验,可能会造成评判结论模糊这一问题,引入了粗糙理论来计算评价指标的客观权重,并将模糊中心理论应用于隧道坍塌风险评价中。
由于采用层次分析(AHP)法、概率分析事故树理论等主观方法确定评价指标权重时过分依赖专家经验易造成误差,而采用理想点法、云模型和粗糙集理论等客观方法确定评价指标权重时需要大量的调查数据,故本文将最常用的主观方法层次分析(AHP)法和客观方法熵权(EW)法相耦合来确定评价指标的综合权重,一方面可以弥补数据的缺失,另一方面可以削弱人为判断引起的误差,并且EW法完全取决于数据,且计算较为客观。未确知信息是一种不同于模糊信息、随机信息和灰色理论信息的新的不确定信息,未确知测度理论能够很好地解决信息的不确定性问题。因此,本文采用EW-AHP和未确知测度理论对隧道坍塌风险可能性进行评价,可为预防和控制隧道坍塌提供理论参考。
1 隧道坍塌风险评价的未确知测度原理
假设评价指标空间A={a1,a2,…,an}有n个,H(h1,h2,…,hm)是每个研究对象的m个评价指标,则可构成ai={ai1,ai2,…,aim}的m维向量,其中aij表示隧道坍塌风险评价指标测度值。将ai划分为s个评价等级,记评价等级R={C1,C2,…,Cs},假设Ce>Ce+1,则称{C1,C2,…,Cs}为评价等级R上的一个有序分割类[10-11]。
1. 1 单指标未确知测度
设βije=β(aij∈Ce)表示测度值aij属于第e个评价等级Ce的程度,要求β满足以下三式:
(1)
(i=1,2,…,n;j=1,2,…,m;l=1,2,…,e)
根据未确知测度的定义,首先构造隧道坍塌风险评价单指标测度函数β(aij∈Ce),求出某评价因素ai的各评价指标测度值βije,βije表示测量值aij属于第e个评价等级的程度,且满足公式(1)所对应的“非负有界性”、“归一性”和“可加性”。
各单指标测度值βije构成的评价矩阵如下:
(2)
1.2 基于EW-AHP确定评价指标的权重系数
1.2.1 熵权法确定评价指标的客观权重
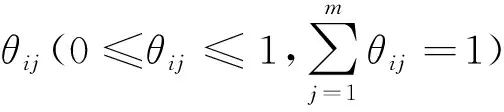
(3)
(4)
1.2.2 层次分析法确定评价指标的主观权重
层次分析(AHP)法是一种主观赋权方法,该方法首先将已经确定的引起隧道坍塌风险的因素按照9级标度法进行两两比较,构成判断矩阵S;然后用方根法计算判断矩阵,得到各因素的权重;最后对判断矩阵进行一致性检验,当随机一致性比率CR小于0.1时则认为层次分析排序的结果满意,即权系数的分配是合理的;否则,需要调整判断矩阵的因子取值,重新计算。
1.2.3 乘法合成归一化方法确定评价指标综合权重
复合权值是客观数据与主观经验的耦合,本文运用乘法合成归一化方法计算评价指标的综合权重[12-13],具体计算公式如下:
(5)
式中:ωj为第j个评价指标的综合权重;αj、βj分别为第j个评价指标的主、客观权重;m为评价指标的个数。
1. 3 多指标综合测度

2 实例应用与分析
2. 1 研究区概况
研究区为新疆某地区3条特长引水隧道。其中,西二隧道洞身为奥陶系黑云母石英片岩、二云石英片岩以及华力西期变质斜长花岗岩、花岗斑岩、闪长岩,花岗岩中石英含量一般为15%~25%,为中硬—坚硬岩,整体稳定性好,饱和抗压强度为30~170 MPa,隧洞埋深为15~596 m,绝大部分均为Ⅱ、Ⅲ类围岩,石炭系凝灰质砂岩、黑云长英角岩中石英含量一般为20%~30%,花岗岩、黑云母花岗岩、黑云母角闪斜长岩、片麻极少,为Ⅳ、Ⅴ围岩;双三隧道隧洞穿越石炭系(C)、泥盆系(D)和华力西期三大地层,岩性主要为硅质砾岩、安山岩,局部夹凝灰质砂岩、砂岩、沉凝灰岩、石英闪长斑岩、砂砾岩等,石英含量一般为1%~15%,饱和抗压强度为40~130 MPa,隧洞埋深为65~300 m,绝大部分均为Ⅱ、Ⅲ类围岩,极少为Ⅳ、Ⅴ类围岩;喀双隧道沿线地形为剥蚀丘陵地貌,地形略起伏,多发育丘陵,部分地段发育冲沟,无大断裂发育,隧洞洞身为石炭系凝灰岩、凝灰质砂岩,少量石英闪长岩,为坚硬岩,整体稳定性好,饱和抗压强度为20~120 MPa,隧洞埋深为103~790 m,绝大部分均为Ⅱ、Ⅲ类围岩,极少为Ⅳ、Ⅴ围岩。本文在研究区选取了10个具有代表性的区段作为隧道坍塌风险评价的对象。
2. 2 隧道坍塌风险可能性等级评价
2.2.1 确定隧道坍塌风险可能性的评价等级
参照文献[4]中风险事件的可能性等级,本文建立隧道坍塌风险可能性的评价等级R={C1,C2,…,C5},其中C1~C5分别表示“很可能”、“可能”、“偶尔”、“可能性很小”、“不可能”。
2.2.2 隧道坍塌风险评价指标的选取
隧道坍塌风险评价指标的选取一方面要依据是否容易获取且可操作性强,另一方面要根据待评价隧道的施工现状、地质条件和风险特征等情况进行合理筛选。
通过对已有的研究成果进行汇总,归纳出造成隧道坍塌风险的主要因素有地质条件因素、设计因素、施工因素,并根据朱捷等[2]对381个隧道坍塌案例的概率统计分析得到的主要影响因素为围岩级别(18.35%)、地下水(11.15%)、降雨(10.19%)、支护方式(7.29%)、断裂破碎带(6.90%)、岩体完整性(6.13%)、隧道埋深(4.39%),而降雨一般考虑在隧道洞口或浅埋段,故本文不予考虑。此外,结合国外学者的相关研究[2],还应充分考虑隧道断面设计因素和施工因素。最终本文选择了3个定量评价指标和8个定性评价指标,即等效截面积X1(m2)、深度比X2、断裂破碎带宽度X3(m)、单轴抗压强度X4(MPa)、地下水状况X5、RQDX6(%)、岩石风化程度X7、超挖X8(%)、支护方式X9、围岩等级X10、岩体完整性X11。研究区隧道坍塌各评价指标的调查数据和具体分级标准见表1和表2。部分评价指标描述如下:
(1) 等效截面积(X1):隧道断面积越大,隧道越不稳定,越容易发生坍塌,该评价指标的等级划分标准主要依据实测数据[14]。
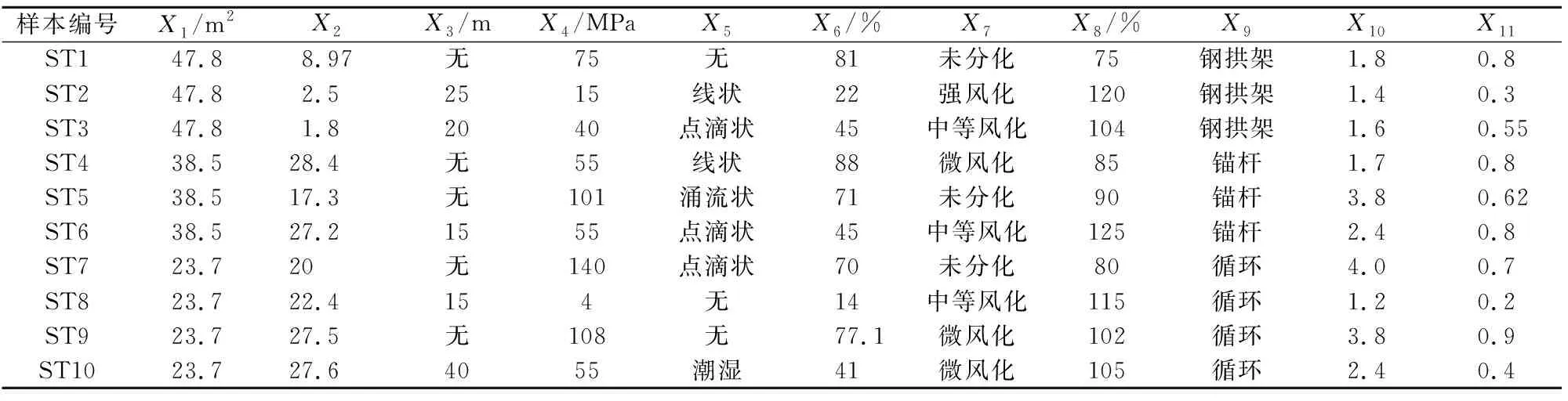
表1 研究区隧道坍塌调查信息表

表2 隧道坍塌风险评价指标的分级标准
(2) 深度比(X2):表示的是隧道埋深与隧道直径的比值(z0/D),根据有关研究表明该深度比值越大,隧道坍塌的风险越小。
(3)RQD(X6):表示岩石质量指标值,可以用来反映隧道的地质状况。
(4) 围岩等级(X10):隧道围岩的强度和完整性对隧道围岩的稳定性有很大的影响,随着隧道岩体强度的降低,隧道围岩的稳定性降低,纵波可以作为隧道围岩等级的判断标准。

2.2.3 构造单指标测度函数
以样本ST4为例,图1为隧道坍塌风险各评价指标的单指标测度函数。 由表1的研究区隧道坍塌调查信息表,即可求出样本ST4的单指标测度值βije构成的评价矩阵如下:
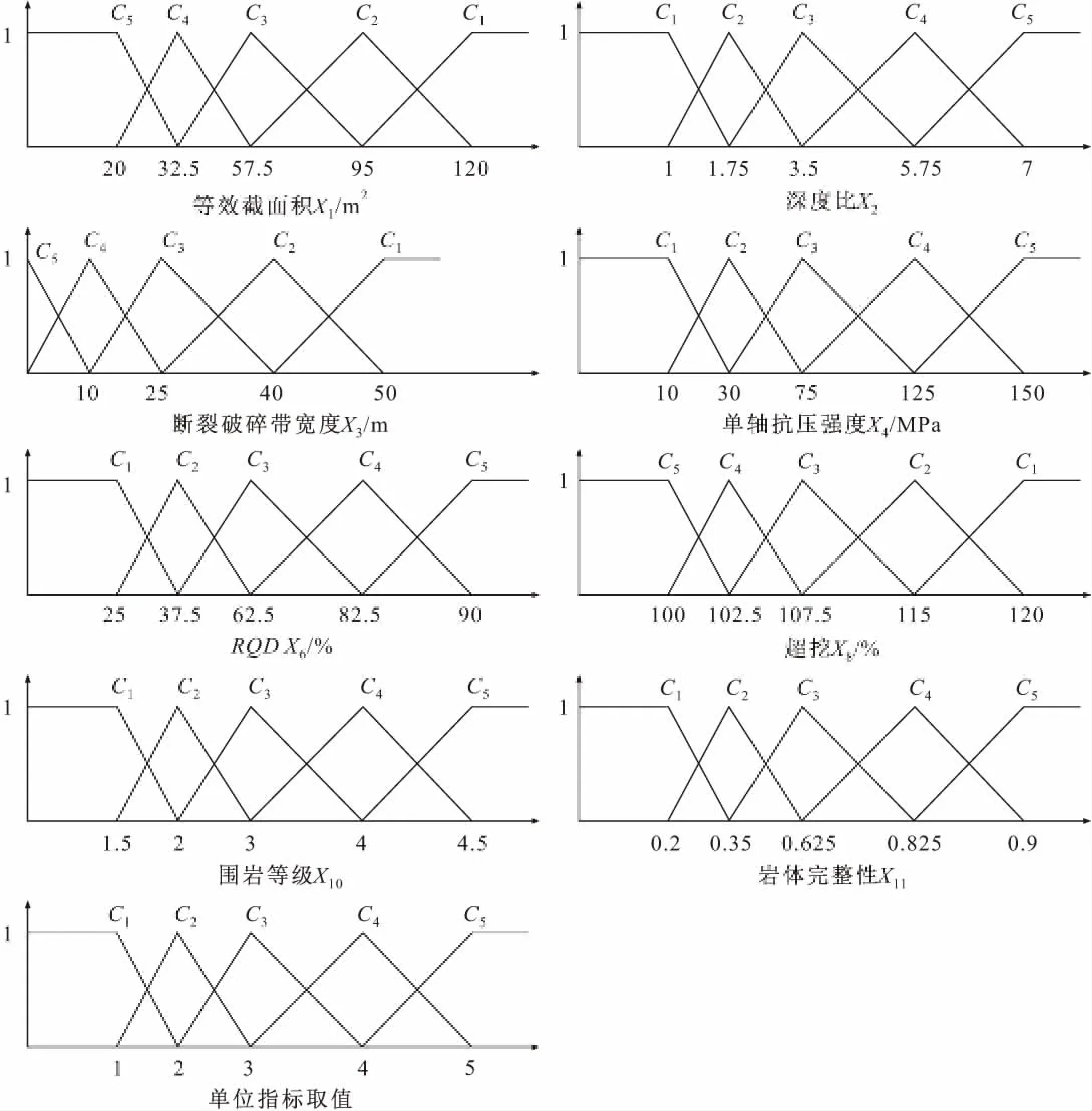
图1 隧道坍塌风险各评价指标的单指标测度函数Fig.1 Single index measure function of each evaluation index of tunnel collapse risk
C5C4C3C2C1
(6)
2.2.4 基于EW-AHP确定评价指标的综合权重
将主观方法AHP法和客观方法EW法进行耦合,并通过公式(5)计算各评价指标的综合权重。以样本ST4为例,具体计算过程如下:
(1) AHP法确定评价指标的主观权重:将11个评价指标按照AHP法中的9级标度法通过专家评判对各因素的重要性两两比较形成判断矩阵,并进行一致性检验,最终可计算得出各评价指标的主观权重,见表3。
(2) EW法确定评价指标的客观权重:EW法是根据指标的变异程度来确定该评价指标提供信息量的多少,可直接反映该评价指标作用的大小,因此它可作为综合评价中一种指标客观权重的计算方法。根据公式(3)和(4),可计算得到各评价指标的客观权重,见表3。
(3) 乘法合成归一化方法确定评价指标的综合权重:采用乘法合成归一化方法,根据公式(5)将评价指标的主观权重和客观权重进行耦合,可计算得到各评价指标的综合权重,见表3。
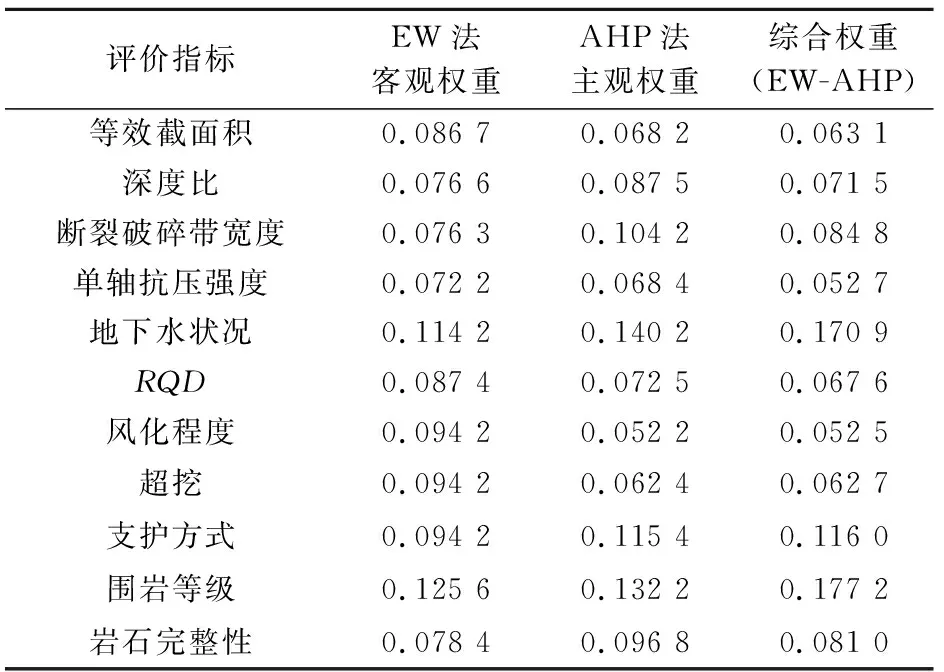
表3 隧道坍塌风险评价指标的综合权重值
2.2.5 确定多指标综合测度评价向量
将样本ST4隧道坍塌风险评价指标的综合权重与其单指标测度评价矩阵[式(6)]进行相乘,则可得到样本ST4的多指标综合测度评价向量为{0.406 8,0.266 4,0.163 5,0.163 3,0},并根据最大隶属度原则,其风险可能性等级为Ⅰ级。采用同样的方法,可求出其他9个样本的多指标综合测度评价向量并获得风险可能性等级,最终的评价结果与现场调查结果对比见表4。

表4 基于EW-AHP和未确知测度理论的隧道坍塌风险评价结果与现场调查结果对比
2. 3 评价结果分析
由表4可以看出:
(1) 样本ST8的隧道坍塌风险可能性等级为Ⅴ级(很可能),经现场调查发现:ST8处左、右拱顶围岩滑塌严重,尤其薄层凝灰岩滑塌高度高达0.5 m,且顺裂隙走向滑塌长度较大,向掌子面延伸。
(2) 样本ST2、ST3、ST10的隧道坍塌风险可能性等级为Ⅳ级(可能),经现场调查发现:ST2处围岩完整性差,岩体呈块裂结构,结构面光滑,拱顶围岩顺结构面滑塌、掉块严重;ST3处围岩裂隙切割强烈,尤其薄层凝灰岩被切割成块体,且裂隙面平直光滑,顺结构面岩体滑塌严重;ST10处拱底发育f51扭性断层,产状为330°NE∠43°,断层破碎带宽度较大,带内岩体为糜棱岩夹断层泥,呈碎裂结构,掉块严重。
(3) 样本ST6的隧道坍塌风险可能性等级为Ⅲ级(偶尔),经现场调查发现:该处围岩完整性相对较完整,隐蔽裂隙发育,局部轻微掉块。
(4) 样本ST1、ST4、ST5、ST7、ST9的隧道坍塌风险可能性等级为Ⅰ级(不可能),经现场调查发现:这几处围岩整体较完整稳定,局部裂隙较发育,开挖后洞壁较为平整光滑。
3 结 论
(1) 本文结合国内外相关研究,选取了11个隧道坍塌风险评价指标,避免了评价指标过多、计算繁杂和数据不易获取等问题,以此建立了隧道坍塌风险评价指标体系,并建立了隧道坍塌风险可能性分级标准。
(2) 本文将主观层次分析(AHP)法与客观熵权(EW)法相耦合,确定了隧道坍塌风险评价指标的综合权重,一方面降低了人为因素的干扰,另一方面弥补了数据量的不足,并采用EW-AHP和未确知测度理论确定研究对象的多指标综合测度评价向量,进而根据隶属度准则确定了隧道坍塌风险可能性等级。
(3) 通过将本文评价方法应用于新疆3条特长引水隧道坍塌风险可能性评价,并将评价结果与现场调查结果进行对比分析,结果表明:其评价结果与实际情况基本一致,可为隧道坍塌风险评价提供参考。
