裂隙水作用下近水平地层滑坡破坏机理研究
2020-09-27殷天赐霍志涛
殷天赐,余 乐,汪 洋,周 浩,姚 鸣,霍志涛
(1.中国地质大学(武汉)工程学院,湖北 武汉 430074;2.中南地质科技创新中心,湖北 武汉 430205;3.湖北省电力勘测设计院有限公司,湖北武汉430040;4.中国地质大学(武汉)地质调查研究院,湖北 武汉 430074)
在近水平甚至反倾地层中发生滑坡的可能性较低,但在我国三峡库区万州区近水平的侏罗系地层中发育有大量的具缓倾角滑面的滑坡,这些滑坡分布面积大、隐蔽性强,且破坏性较大,对其成因机理的研究具有十分重要的意义[1-3],因此吸引了众多国内外学者对这一难题进行探讨和研究。目前学者们对该类滑坡的形成机制认识不一,主要的认识有如下几种:殷坤龙等[4]、罗冲等[5]认为具有膨胀性的软弱夹层是近水平地层发生推移式滑动的主要原因;许强等[6]认为坡体后缘裂缝充水,地下水沿下伏软弱层顶面渗透,在降低软弱层抗剪强度的同时对滑体产生浮托力,在后缘裂隙水的推力与底滑面浮托力联合作用下岩体沿软弱层被水平推动是板梁状滑坡发生的主要原因;抗兴培等[7]、王飞等[8]研究了裂缝和裂缝水诱发黄土类滑坡的原因,分析了其成因机理及演化过程,并总结了该类滑坡的防治措施;Ayalew等[9]认为软弱岩层受上覆硬质岩层的挤压是水平地层发生滑动的原因;Lourenco等[10]、Floris等[11]采用室内实验手段对不同渗透率土体中孔隙水压力的产生机理进行了研究,并探寻了孔隙水压力与坡体变形破坏模式之间的关系。然而这些观点都没有详细考虑在后缘陡倾裂隙中不同充水高度时的裂隙水压力作用下近水平地层滑坡滑带受力与破坏的动态演化过程,没有理清后缘裂隙中裂隙水压力是否对滑坡破坏产生影响,有多大的影响,怎么影响等诸多问题。基于此,本文采用理论分析的手段,运用弹塑性力学的相关理论,对这些问题进行了分析和求解,对裂隙水作用下近水平地层滑坡的成因机理进行了探讨。
1 裂隙水作用下近水平地层滑坡破坏机理分析
1. 1 平面问题的应力解
在空间力系的作用下,弹性物体的应力和应变状态均是关于空间坐标的函数,这即为弹性力学的空间问题。然而对于特殊形状的弹性物体在特殊荷载作用下,空间问题便可近似地简化为平面问题来处理。因此,根据近水平地层滑坡的形状特征和受力特征,可将其简化为平面应力问题,并可采用平面问题的直角坐标解来求解滑坡中任意一点的应力,然后根据强度准则,可以判断滑坡中任意一点的破坏情况。根据不同工况下滑坡中任意一点的应力及破坏情况,即可对滑坡的破坏模式和启动条件进行理论的计算研究。
按应力求解弹性力学问题时,所求的应力分量应满足平衡微分方程和变形协调方程,应力分量在边界上应满足应力边界条件。而物体表面各点处的应力分量应当与作用在该点处的面力相平衡,这种关系构成了变形固体内的应力场所必须满足的边界条件。平面问题中物体的边界与坐标Z轴相平行(即在xoy平面内讨论问题),其静力边界条件可简化为
(1)
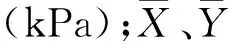
物体在外力作用下处于平衡状态时,其内部各点的应力状态是各不相同的,描述各微元体上应力分量所满足的平衡条件的方程就是平衡微分方程。在平面应力问题上,因τyz=τzx=0,且其他应力分量均与坐标Z轴无关,同时有体力分量Fz=0,故平面问题的平衡微分方程可简化为
(2)
上式为非齐次线性微分方程组,所以它的通解是该方程组的任一特解与相应的齐次方程组的通解之和。其特解为
σx=-Fxx
σy=-Fyy
τxy=0
将该特解代入平衡微分方程即可验证其正确性。
平衡微分方程对应的齐次方程组为
求解出该齐次方程组的通解为
于是平面问题的平衡微分方程的通解为
(3)
平面问题若采用应力解法,基本未知量有3个:σx、σy、τxy,而平衡微分方程只有2个,因此需要用变形协调方程作为补充。对于平面应力问题可放松变形协调方程的,近似地认为平面应力问题只要满足下式即可完全满足变形协调方程:
(4)
利用各向同性体应力-应变关系式,用应力分量表示上式中的应变分量并化简,可得:
(5)
当体力分量Fx、Fy为常量时,将平衡微分方程的通解[公式(2)]代入上面的变形协调方程,可得:
(6)
展开后,有:

(7)
此方程称为双调和方程,满足此方程的函数φ称为双调和函数。当体力为常量时,平面问题的求解可归结为寻求满足边界条件[公式(1)]的一个双调和函数。
在给定的边界条件下,要直接求解双调和函数φ是很困难的,要先假定满足双调和方程的某种形式的双调和函数φ,然后用平衡微分方程的通解求出应力分量σx、σy、τxy等,再根据应力边界条件来分析所得应力分量对应于什么样的面力,此方法称作逆解法。
1. 2 模型概化
近水平地层滑坡大都发育在倾角小于10°的平缓地层中,滑面沿硬岩与软岩的交界面呈平直分布,滑面产状与岩层产状相同,滑坡后缘具有平行于坡面的陡倾裂隙,降雨时裂隙中充水,且不能很好地排泄出去。根据以上特点建立如图1所示的近水平地层滑坡简化模型。假设滑面水平,后缘裂隙垂直,坡面为一直线且与垂直方向的夹角为α,垂直裂隙的高度为H,滑面长度为T。通过分析受力可知,滑体受重力G、支持力N、摩擦力F、沿滑移面的孔隙水扬压力u(其方向垂直滑面向上,大小为γwH)作用,当后缘裂隙充水且假设其充水高度为H2时, 后缘侧壁受裂隙水压力(该压力与侧壁垂直且成三角形分布,大小为γwH2)作用,在后缘推力的作用下滑面将产生摩擦阻力F,且滑带会从后向前逐渐破坏。
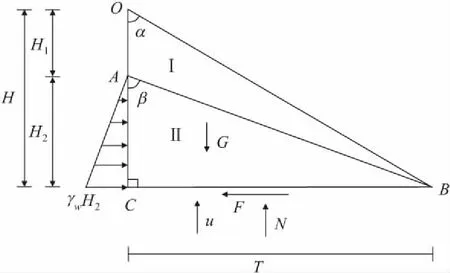
图1 近水平地层滑坡简化模型Fig.1 Simplified model of near-horizontal stratum landslide
1. 3 滑带应力计算
为了探讨后缘裂隙充水高度动态变化时滑带的受力与破坏机理,将近水平地层滑坡简化模型拆分为Ⅰ和Ⅱ两个部分:第Ⅰ部分滑体只受重力作用,且该部分重力最后以压应力的形式沿AB边作用到第Ⅱ部分上,见图2;第Ⅱ部分滑体除了在AB边受上部滑体的压应力作用外,在AC边受静水压力作用,在BC边受支持力N、摩擦力F和孔隙水扬压力u作用,见图3。
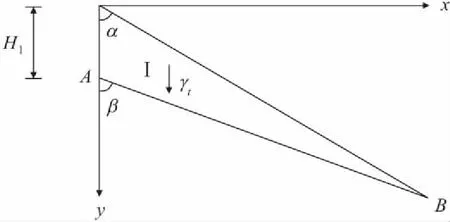
图2 近水平地层滑坡简化模型Ⅰ示意图Fig.2 Schematic diagram of the simplified model Ⅰ of near-horizontal stratum landslide
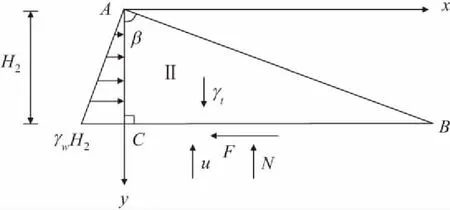
图3 近水平地层滑坡简化模型Ⅱ示意图Fig.3 Schematic diagram of the simplified model Ⅱ of near-horizontal stratum landslide
在模型Ⅰ中,滑体内任意一点的应力分量由重力引起(支撑力和摩擦力也是自重的函数),由于重力与岩土体的容重γt成正比,其量纲为[力]/[长度]3,而应力分量σx、σy、τxy的量纲为[力]/[长度]2,x、y的量纲为[长度],α、β为无量纲量,所以根据量纲分析,应力分量的表达式为γt·x、γt·y这两项的组合,即应力分量的表达式只可能是x和y的一次式,又根据应力分量是应力函数φ对x、y的二阶导数,故假设:
φ=Ax3+Bx2y+Cxy2+Dy3
(8)
在模型Ⅰ中:体力Fx=0、Fy=γt,由平衡微分方程的解可知:
(9)
列出边界条件:
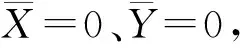
(10)
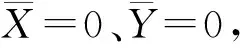
(11)
联立公式(10)和(11),可求得:
B=C=D=0
将其代入公式(9),可得:
于是AB边界y=xcotβ+H1上任意一点的应力分量为
此时对AB边界,有:
m=-cosβ,n=sinβ
在模型Ⅱ中,滑体内任意一点的应力分量由重力和水压力引起(支撑力、摩擦力、孔隙水扬压力也是自重或水压力的函数),由于这几种力与岩土体和水的容重γt、γw成正比,其量纲为[力]/[长度]3,而应力分量σx、σy、τxy的量纲为[力]/[长度]2,H、T、x、y的量纲为[长度],α、β为无量纲量,所以根据量纲分析,应力分量的表达式为γt·x、γt·y、γt·H、γt·T、γw·x、γw·y、γw·H、γw·T这8项的组合,即应力分量的表达式可能是x和y的一次或零次式,又根据应力分量是应力函数φ对x、y的二阶导数,故假设:
在模型Ⅱ中:体力Fx=0、Fy=γt,由平衡微分方程的解可知:
(12)
列出边界条件:
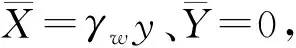
(13)
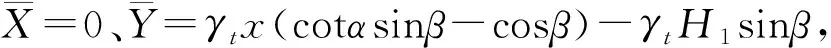
(14)
联立公式(13)和(14),可求得:
A=γt(2cotβ-cotα)-2γwcot3β
B=γwcot2β
D=-γw
E=γtH1
F=0
G=0
将其代入公式(12),可得:
于是BC边界y=H2上任意一点的应力分量为
(15)
弹性力学中对应力分量的正负号有如下规定:单元体截面外法线的指向与坐标轴正方向一致的面称为正截面,与坐标轴负方向一致的面称为负截面;正截面上应力分量指向同坐标轴正方向一致者为正,反之为负;负截面上应力分量指向同坐标轴负方向一致者为正,反之为负。此外,弹性力学中规定拉应力为正,压应力为负。
1. 4 强度准则
强度准则是指在复杂应力状态下,岩土材料出现宏观裂纹或发生破坏时应力之间所满足的条件。在岩土力学中,强度准则的含义是指岩土体中单元体的任何微截面上的剪应力τ都不能超过某一临界值,否则岩土材料就会产生剪切滑移,而这一临界值与破裂面上的正应力σ之间存在线性关系,即有:
τ=c-σtanφ
(16)
这就是库伦剪切强度准则,由于弹性力学中取压应力为负,与岩土力学中相反,因此σ前的符号为负。
将滑带上任意一点的垂向应力σy代入公式(16)中,计算得到该点处微单元体的抗剪强度为
τmax=-σytanφ+c
(17)
当τxy<τmax时,该点处微单元体处于平衡状态;当τxy>τmax时,该点处微单元体发生破坏。
2 近水平滑坡实例分析
2. 1 大包梁滑坡概况
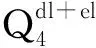

图4 大包梁滑坡区地形地貌图Fig.4 Landform of Dabaoliang landslide area
2. 2 模型参数选取
根据大包梁滑坡的形态特征和物质组成,为了便于计算求解,对大包梁滑坡模型进行适当简化,简化后的模型见图5,模型材料物理力学参数来自于室内试验和现场试验测试,具体参数值见表1。
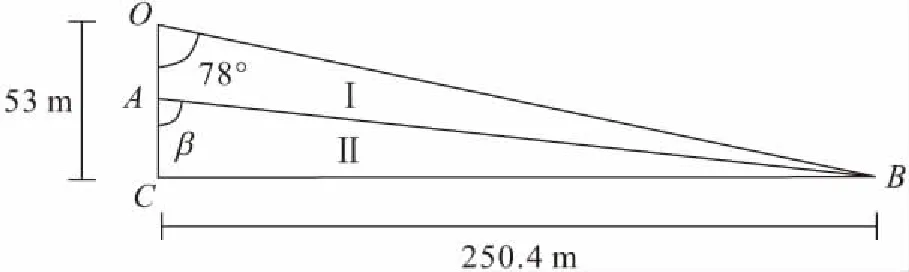
图5 大包梁滑坡模型简化图Fig.5 Schematic diagram of Dabaoliang landslide simplified model

表1 大包梁滑坡模型材料物理力学参数
2. 3 计算工况与结果分析
为了详细了解大包梁滑坡滑带在后缘裂隙中不同充水高度的裂隙水作用下的启动破坏条件,依次建立5种工况,各工况的条件如下:
(1) 工况1:当后缘裂缝中水深H2=0.2H=10.6 m,H1=H-H2=42.4 m时,联立方程(15)、(16)、(17)后解得2.59x2-1 470.19x+207 548.07<0时该点破坏,故解一元二次方程得265.44 (2) 工况2:当后缘裂缝中水深H2=0.4H=21.2 m,H1=H-H2=31.8 m时,联立方程(15)、(16)、(17)后解得0.381x2-293.63x+56 991.08<0时该点破坏,由于解该一元二次方程Δ<0,即方程无解,说明此时滑面上没有岩土体发生破坏。 (3) 工况3:当后缘裂缝中水深H2=0.6H=31.8 m,H1=H-H2=21.2 m时,联立方程(15)、(16)、(17)后解得0.276x2-30.449x-801.38<0时该点破坏,故解一元二次方程得-132.27 (4) 工况4:当后缘裂缝中水深H2=0.8H=42.4 m,H1=H-H2=10.6 m时,联立方程(15)、(16)、(17)后解得2.442x2-544.55x+27 310.67<0时该点破坏,故解一元二次方程得76.17 (5) 工况5:当后缘裂缝中水深H2=H=53 m,H1=H-H2=0 m时,联立方程(15)、(16)、(17)后解得6.872x2-1 976.27x+138 807.75<0时该点破坏,故解一元二次方程得121.95 考虑到各个工况下滑体应力和剪力图趋势一致,现以工况1为例,研究该滑坡应力和剪力的变化趋势,见图6和图7。 图6 工况1下大包梁滑坡滑带各应力分量分布图Fig.6 Distribution of stress components of the sliding surface of Dabaoliang landslide in working condition 1 由图6可见,在充水高度为Hw2=10.6 m的后缘裂隙水的作用下,大包梁滑坡滑带上的各应力分量表现为:应力分量σx=103.88 kPa,大小恒定,为受压状态;应力分量σy呈三角形分布,左侧σy最大值为1 356.45 kPa,沿滑带往右逐步减小,直至为0 kPa,但均为受压状态;应力分量τxy呈三角形分布,左侧τxy最小值为0 kPa,沿滑带往右逐步增大,直至为4.41 kPa,但数值整体很小。 图7 工况1下大包梁滑坡滑带剪应力大小对比图Fig.7 Comparison diagram of shear stress of the sliding surface of Dabaoliang landslide in working condition 1 由图7可见,在工况1下,大包梁滑坡滑带上各点的剪应力分量τxy均小于抗剪强度τmax,此时滑带不发生破坏。 (1) 本文基于近水平地层滑坡特征建立了力学概化模型,并基于弹性解析法计算出了该类滑坡滑带处3个应力分量的表达式,同时选取有效的强度准则依据滑带处各点的应力判断其破坏情况。 (2) 运用该理论通过对大包梁滑坡进行实例分析,判断了不同充水高度的后缘裂隙水压力作用下该滑坡滑带的破坏情况,结果表明:在不同后缘裂隙水压力作用工况下,该滑坡滑带破坏的趋势为水压高度从0上升到2/5H时,滑带不破坏;当水压继续增大时,滑带开始破坏。应用弹性力学方法,对裂隙水压力作用下大包梁近水平地层滑坡滑带的应力进行计算,得到滑带应力分量分布图,结果显示:应力分量σx沿滑带呈矩形分布,大小不变,为压应力;应力分量σy沿滑带呈三角形分布,左端最大,右端为0,均为压应力;应力分量τxy沿滑带呈三角形分布,左端为0,右端最大。该研究结果对近水平地层滑坡成因机理和启动机制的研究具有重要的参考意义。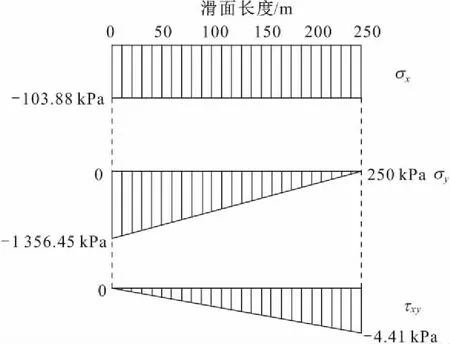
3 结 论
