浅谈如何解决中考数学中的创新型问题

2020-09-26刘宗安

考试周刊 2020年79期

摘要：文章结合近年中考数学试题，从阅读理解问题、开放型问题、探索型问题、分类讨论问题、跨学科问题、图象与图表信息问题等六种中考數学常见问题，阐述如何解答中考数学中的创新型问题。

关键词：中考数学试题;数学素养;创新能力

纵观近年各地中考数学试题，创新型问题成为一个新的亮点，这类问题立意新颖、构思精巧、形式多样，从题材的选材，文字的表达到题型的设计，都颇具特色。它有利于提高学生的数学素养，培养学生的创新能力。文章从近年各地中考试题中选出几题予以剖析，也许还不成熟，敬请老师们批评指教。

一、阅读理解问题

阅读理解题常见的类型有：（1）阅读新知识，解决新问题;（2）阅读解题过程，模仿解题策略;（3）概括归纳型;（4）阅读纠正错误，提高辨别能力。

【例1】（2019·枣庄）对于实数a、b，定义关于“”的一种运算：ab=2a+b，例如34=2×3+4=10。

（1）求4（-3）的值;

（2）若x（-y）=2，（2y）x=-1，求x+y的值。

简析：（1）依据关于“”的一种运算：ab=2a+b，即可得到4（-3）的值;（2）依据x（-y）=2，（2y）x=-1，可得方程组2x-y=2 ①x+4y=-1 ②，即可得到x+y的值。

答案：（1）4（-3）=5;（2）x+y=13

点评：本题主要考查解二元一次方程组以及有理数的混合运算的应用，根据题意列出方程组是解题的关键。阅读理解题主要考查学生的阅读能力和对所学知识的整理、归纳能力。阅读理解题多以新运算、新概念、新方法的形式呈现。解决这类问题的关键要把握两点：一是掌握问题原型的特点及解决问题的思想方法;二是根据问题情境的变化，把握其规律，领会问题的本质内容，合理进行思想方法的迁移。

二、开放型问题

开放型问题有三种类型：（1）条件开放型（条件在不断变化）;（2）结论开放型（结论有多个或结论无固定）;（3）策略开放型（思维的方法和思维的途径有多种）。

【例2】（2019·齐齐哈尔）如图，已知在△ABC和△DEF中，∠B=∠E，BF=CE，点B、F、C、E在同一条直线上，若使△ABC≌△DEF，则还需添加的一个条件是（只填一个即可）。

简析：由已知可证BC=EF，又∠B=∠E，要使△ABC≌△DEF，有三种思路可供选择：（1）若根据SAS，则可填AB=DE;（2）若根据ASA，则可填∠ACB=∠DFE（或AC∥DF）;（3）若根据AAS，则可填∠A=∠D。本题主要考查学生对全等三角形判定定理掌握的熟练程度，此类添加条件题是开放型问题，答案并不唯一，只要符合全等三角形的判定定理即可。

答案：添加的条件是：AB=DE或∠ACB=∠DFE（或AC∥DF）或∠A=∠D。

点评：开放性问题常提供一些开放性（在问题的条件、结论、解题策略或应用等方面具有一定的开放程度）的问题，解题时要灵活运用所学基础知识，多层次多角度地分析、思考问题。开放性问题可以使学生从不同角度去探索，留给学生更多的空间去发挥创造，从而培养学生的创新能力。

三、探索型问题

探索型问题的类型有两种：1. 结论探索型问题（在给定的题设条件下，去寻求某种结论的一类问题）;2. 存在探索型问题（在某种题设条件下，判断具有某种性质的数学对象是否存在）。

【例3】（2018·安顺）正方形A1B1C1O，A2B2C2C1，A3B3C3C2，…按如图的方式放置，点A1，A2，A3…和点C1，C2，C3…分别在直线y=x+1和x轴上，则点Bn的坐标为。

简析：根据一次函数图象上点的坐标特征可得出点A1的坐标，结合正方形的性质可得出点B1的坐标，同理可得出点B2、B3、B4、…的坐标，再根据点的坐标的变化即可找出点Bn的坐标。

答案：（2n-1，2n-1）。

点评：本题考查了一次函数图象上点的坐标特征和正方形的性质，通过推导得出点的坐标的变化规律是解题的关键。本题是规律探索型问题，解题时先从较简单的特例入手，从中探索出规律，再用得到的规律解答问题即可。解结论探索型问题时，应根据条件从多角度进行分析，联想有关性质及定理，确定符合条件的结论。解存在探索型问题时，通常先假设被探索的数学对象存在，并将其构造出来，再利用题设条件及有关性质，将其肯定或否定。这类试题主要考查学生分析问题和解决问题的能力和创新意识。

四、分类讨论问题

分类讨论问题常见的类型有五种：1. 以数学概念、定义标准分类;2. 以性质、公式，使用的条件为标准分类;3. 以字母的取值情况或范围为标准分类;4. 以图形的位置关系或形状分类;5. 以图形的对应关系为标准分类。

【例4】（2016·怀化）等腰三角形的两边长分别为4cm和8cm，则它的周长为（）

A. 16cmB. 17cm

C. 20cmD. 16cm或20cm

简析：根据等腰三角形的性质，本题分两种情况讨论。当腰长为4cm或是腰长为8cm两种情况。

答案：C

点评：本题考查了等腰三角形中的常见分类讨论思想，解分类讨论问题的关键是要弄清引起分类讨论的原因，明确分类讨论的对象和标准，不同的标准分类的结果也不同;分类必须做到不遗漏，不重复。

五、跨学科问题

跨学科问题的考查是近年中考的特色之一，这类问题在考查数学知识的同时常与理、化、生、计算机乃至文、史、哲、艺术等方面联系或与现实生活中某方面的联系。

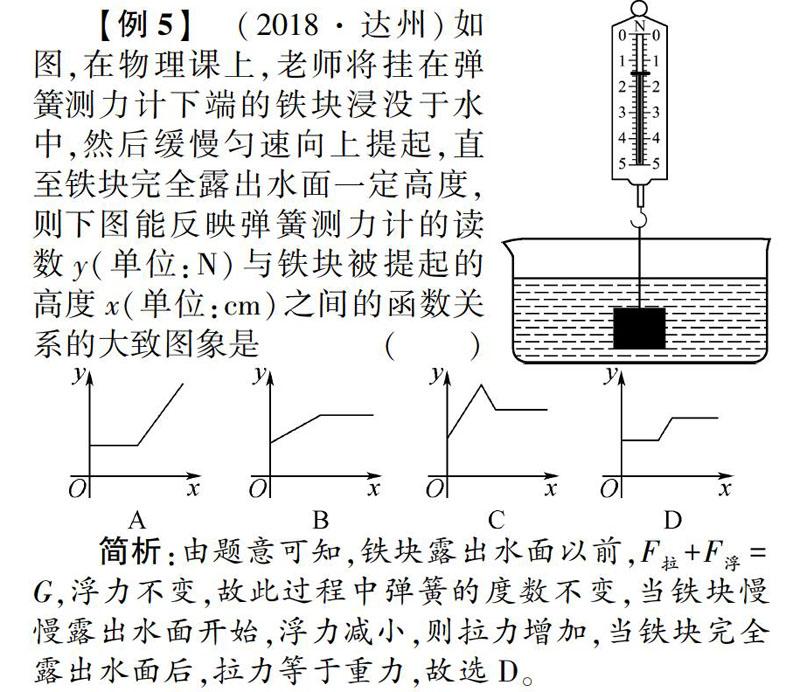
【例5】（2018·达州）如图，在物理课上，老师将挂在弹簧测力计下端的铁块浸没于水中，然后缓慢匀速向上提起，直至铁块完全露出水面一定高度，则下图能反映弹簧测力计的读数y（单位：N）与铁块被提起的高度x（单位：cm）之间的函数关系的大致图象是（）

简析：由题意可知，铁块露出水面以前，F拉+F浮=G，浮力不变，故此过程中弹簧的度数不变，当铁块慢慢露出水面开始，浮力减小，则拉力增加，当铁块完全露出水面后，拉力等于重力，故选D。

答案：D

点评：本题是跨学科试题，本题与物理知识有关，主要考查函数图象，解答本题的关键是明确题意，利用数形结合和分类讨论的数学思想解答。从各地近年中考命题来看，学科之间相互渗透是一种发展趋势，它有利与高考接轨。

六、图象与图表信息问题

图象与图表信息问题的考查已成为近年中考数学命题的一个显著特点，一些取材于社会生活中的实际问题是通过表格、图象等形式把信息提供给学生，要求学生能够运用所学知识解决实际问题。

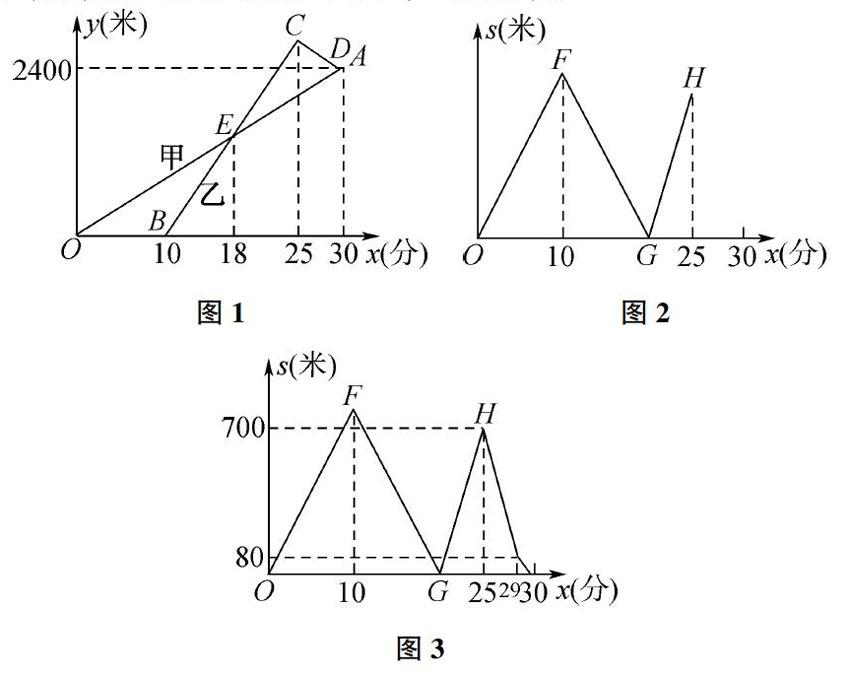
【例6】（2019·湖州）某校的甲、乙两位老师同住一小区，该小区与学校相距2400米。甲从小区步行去學校，出发10分钟后乙再出发，乙从小区先骑公共自行车，途经学校又骑行若干米到达还车点后，立即步行走回学校。已知甲步行的速度比乙步行的速度每分钟快5米。设甲步行的时间为x（分），图1中线段OA和折线B-C-D分别表示甲、乙离开小区的路程y（米）与甲步行时间x（分）的函数关系的图象;图2表示甲、乙两人之间的距离s（米）与甲步行时间x（分）的函数关系的图象（不完整）。

根据图1和图2中所给信息，解答下列问题：

（1）求甲步行的速度和乙出发时甲离开小区的路程;

（2）求乙骑自行车的速度和乙到达还车点时甲、乙两人之间的距离;

（3）在图2中，画出当25≤x≤30时s关于x的函数的大致图象。（温馨提示：请画在答题卷相对应的图上）

简析：（1）根据函数图象中的数据可以求得甲步行的速度和乙出发时甲离开小区的路程;

（2）根据函数图象中的数据可以求得直线OA的函数解析式，然后将x=18代入直线OA的函数解析式，即可求得点E的纵坐标，进而可以求得乙骑自行车的速度和乙到达还车点时甲、乙两人之间的距离;

（3）根据题意可以求得乙到达学校的时间，从而可以将函数图象补充完整。

答案：（1）甲步行的速度是80米/分，乙出发时甲离开小区的路程是800米;

（2）乙骑自行车的速度是180米/分，乙到达还车点时甲、乙两人之间的距离是700米;

（3）当25≤x≤30时s关于x的函数的大致图象如上图所示：

点评：本题考查一次函数的应用，解答本题的关键是明确题意，利用一次函数的图象性质和数形结合的思想解答。图象与图表信息问题通过表格、图象提供的信息，考查学生通过读表、读图获取信息的能力。

说明：中考数学中的创新型问题还有很多，如图形设计问题、实验与操作问题等，限于篇幅，不再例举。