“基于MATLAB的高压直流输电系统小扰动稳定性分析仿真”教学研究
2020-09-26汪娟娟叶运铭黄星海
汪娟娟,叶运铭,黄星海
(华南理工大学 电力学院,广州 广东 510641)
在传统小扰动稳定性分析课程教学中,学生普遍反映课程涉及原理多样抽象,所用公式零散复杂,理解起来十分困难,对学生的考查也仅停留在针对一个二阶或三阶的简单系统进行线性化计算上,使学生在面对高阶系统时往往束手无策。随着编程语言和仿真工具的不断发展,运用电磁暂态仿真软件(如PSCAD/EMTDC)可方便地构建与实际模型具有相同代数关系和电磁关系的电磁模型,有助于学生加深对小扰动分析法的理解,但仅仅通过电磁仿真仍然无法使学生透彻理解小扰动分析法的本质。
“基于MATLAB的高压直流输电系统小扰动稳定性分析仿真”课程,主要讲述如何在 MATLAB中对高压直流输电系统进行建模、仿真和小扰动稳定性分析,是电气工程及其自动化专业的重要课程之一。该课程不仅需要学生具备数学、电路、自动化、计算机等学科的基础知识,还由于其较强的理论性与工程实践性特点,从而是一门集综合性、复杂性和应用性于一体的专业实践课。与传统小扰动稳定性分析课程相比,该课程能够让学生在 MATLAB仿真中,直观感受系统参数变化对系统小扰动稳定性的影响。
本文结合实际教学经验,以高压直流整流侧系统为研究对象,详细介绍在 MATLAB中进行系统小扰动稳定性分析的过程,以期在电磁仿真的基础上,帮助学生深刻理解小扰动分析法。首先,在 MATLAB软件中建立高压直流整流侧系统数学模型,并对该模型进行线性化,得到小干扰动态模型;然后在电磁暂态仿真软件(PSCAD/EMTDC)中搭建高压直流整流侧系统电磁模型,对小干扰动态模型的正确性进行仿真验证;最后应用小干扰动态模型进行系统小扰动稳定性分析的仿真演示。
1 MATLAB功能简介
MATLAB是美国 MathWorks公司出品的商业数学软件,提供用于算法开发、数据可视化、数据分析以及数值计算的高级技术计算语言和交互式环境。它的基本数据单位是矩阵,且其指令表达式与数学、工程中常用的形式十分相似,所以用 MATLAB解算问题要比用C、FORTRAN等语言更加简捷[1]。
在高压直流输电系统小扰动稳定性分析仿真教学中,主要利用 MATLAB进行矩阵运算、实现算法和绘制函数及数据等功能。MATLAB具有强大的算法实现功能,包括非线性方程组和微分方程组在内的复杂算法均可在其中高精度地实现。高压直流输电系统是一个非线性系统,使用 MATLAB易于搭建和调试与本课程内容相关的模型。
2 MATLAB实验教学应用实例
2.1 小扰动稳定性分析
目前的小扰动分析法主要是基于李雅普诺夫线性化方法[2]。高压直流输电系统在运行时无时无刻不受到一些小扰动的影响,如电源的轻微起伏和控制器指令值的微小变化等。这些小的扰动通常不会改变系统的结构,由于其强度足够小,以致系统受到小扰动前后的运行状态十分接近,此时系统的行为可通过其线性化模型进行分析[3]。
为简化起见,本文在 CIGRE标准测试模型基础上,将两端 LCC-HVDC系统的逆变侧等效为一个理想的直流电压源,仅探讨整流侧高压直流输电系统,该系统的换流阀为12脉波。图1为所研究系统的结构图及其单线原理图,其中交流滤波器参数与文献[4]附录中的整流侧交流滤波器参数一致。
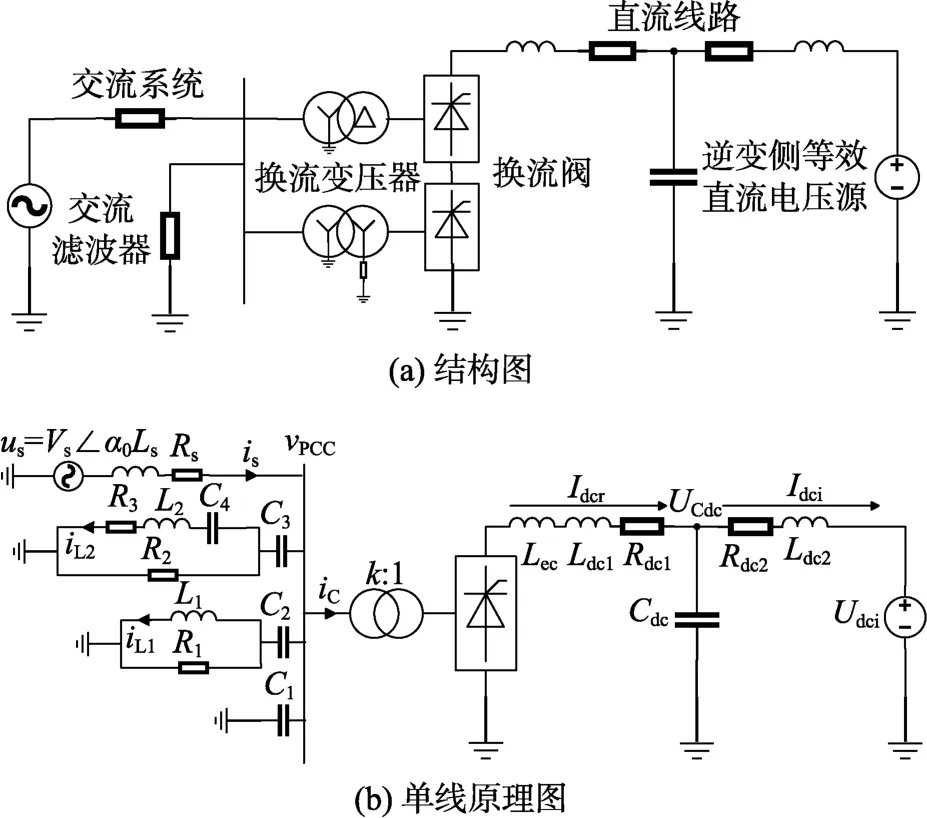
图1 LCC-HVDC系统结构
图1 (b)中:us为交流系统电网电压;RS和LS分别代表交流系统的等值电阻和等值电感;iS为交流系统输出的电流;vPCC为公共连接点(point of common coupling,PCC)电压,R1—R3,L1、L2和 C1—C4分别代表交流滤波器组内相关支路的电阻、电感和电容;iC为换流变压器网侧电流;k为换流变压器变比;Rdc1(Rdc2)和Ldc1(Ldc2)分别代表直流线路整流(逆变)侧等值电阻和电感;Lec为换流变压器对直流侧的等效影响电感;Cdc为直流输电线路等值对地电容;Idcr为整流侧直流电流;Idci为理想直流电压源侧直流电流;UCdc为直流输电线路中点对地电压;Udci为逆变侧等效理想直流电压源电压;α0为交流系统电网电压的初相位。
下面以上述系统为例,从建立系统的状态空间模型开始,逐步叙述如何在MATLAB中建立小干扰动态模型,并利用该模型对系统小扰动稳定性分析进行仿真演示。
2.2 系统的状态空间模型
2.2.1 换流器的建模
基于调制理论的换流器开关函数模型具有物理概念清晰、计算简单、能够揭示谐波产生机理等优点,被广泛用于建立换流器模型[5]。经过基频开关函数的调制,12脉波换流器交、直流侧电流间的关系可表示为:
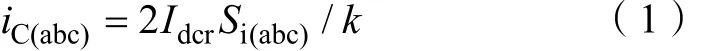
式中,iC(abc)为流经换流变压器网侧的等效三相电流;Si(abc)表示直流电流与等效交流三相电流之间的开关函数,其表达式如下[6]:
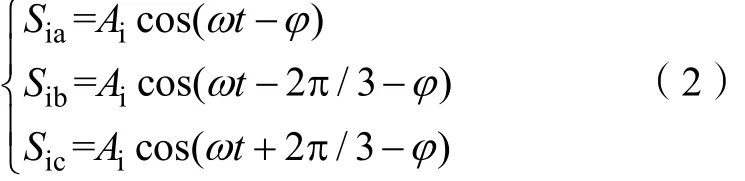
式中,Ai表示换流器换相过程的电流修正系数[7];φ为换流器功率因数角;ω为系统角频率。Ai和φ的表达式为:
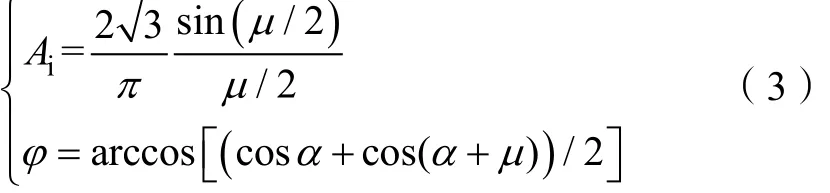
式中,μ为换相重叠角;α为触发延迟角。
经过恒功率Park变换后,换流变压器网侧等效电流iC的d、q轴电流分量为:
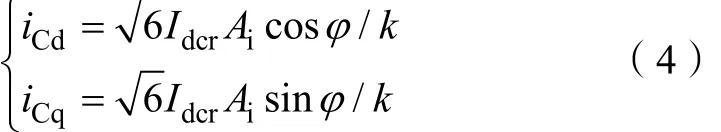
2.2.2 定电流控制器的建模
图 2为整流器定电流控制器的原理图[8],由图可得其状态空间方程如式(5)[9]。
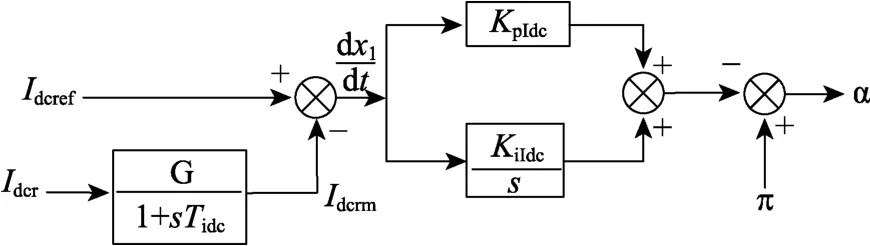
图2 定电流控制器原理框图
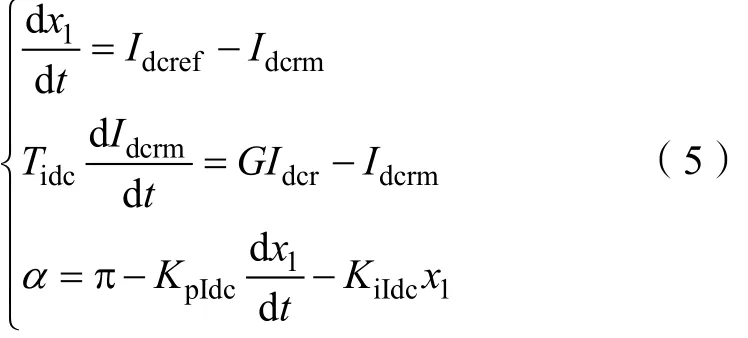
式中,x1为中间状态变量,并无实际物理意义;G=0.5为一阶惯性环节的放大倍数;Tidc=0.005 s为一阶惯性环节的时间常数;KpIdc和KiIdc分别为定电流控制器的比例系数和积分系数;Idcref为直流电流指令值。
2.2.3 锁相环的建模
锁相环的控制原理可等效为图 3,其相应的状态空间方程如式(6)。
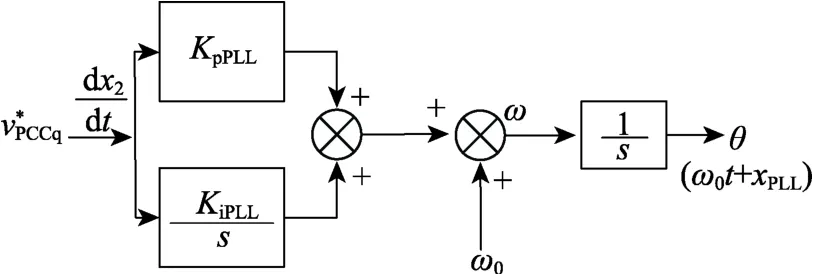
图3 锁相环原理框图

图3及式(6)中,x2为中间状态变量,并无实际物理意义;vPCCq为公共连接点电压的 q轴分量;vP*CCq为vPCCq的标幺值,q轴电压输入到PI环节前进行标幺化的目的是为了消除电压幅值波动对锁相环造成的影响[10];KpPLL和KiPLL分别为锁相环PI环节的比例系数和积分系数;ω为系统角频率;0ω为额定系统角频率;θ为锁相环的输出相位,其初相位为xPLL[11];
2.2.4 交流滤波器及交流系统的建模
由公共连接点的 KCL方程和连接该点各支路的KVL方程,经过恒功率 Park变换后,可得交流滤波器及交流系统的状态空间方程为:

式中,vSd和vSq分别代表交流系统电网电压的d、q轴分量,其相应表达式为:
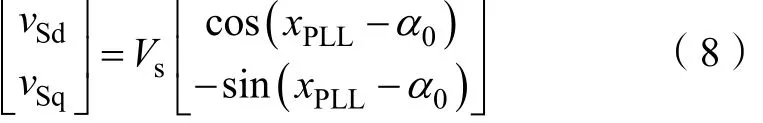
2.2.5 直流输电线路的建模
根据文献[12],换流变压器对直流侧的影响可由一等效电感表示,其表达式为:
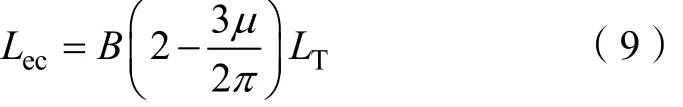
式中,B为6脉动换流单元的个数;TL为换流变压器的漏感。
根据KCL和KVL方程,直流输电线路的状态空间方程为:
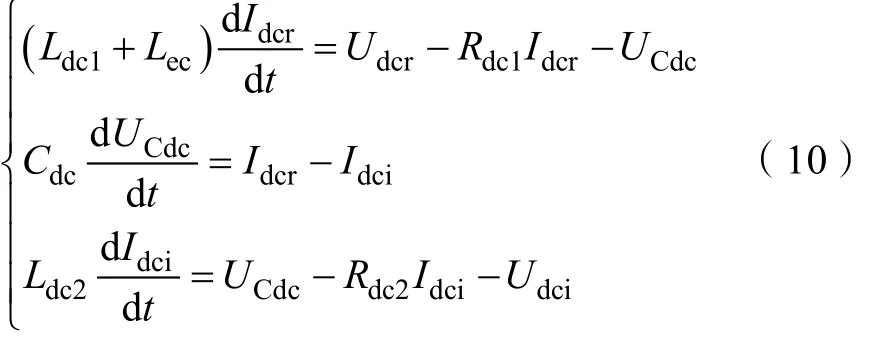
2.3 系统的小干扰动态模型
2.3.1 系统小干扰动态模型的建立
式(1)—(10)囊括了21个非线性微分方程,将这21个方程在平衡点处进行线性化处理,可得系统的小干扰动态模型为[13]:
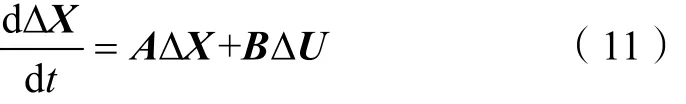
式中,状态变量为X=[vPCCd, vPCCq, vC2d, vC2q, vC3d, vC3q,vC4d, vC4q, iL1d, iL1q, iL2d, iL2q, iSd, iSq, x1, Idcrm, x2, xPLL, Idcr,UCdc, Idci]T;输入变量为 U=Idcref;矩阵A为21×21的系数矩阵;矩阵B为21×1的系数矩阵。
鉴于本文所使用的系统为21阶系统,手动进行线性化计算的工作量较大。当研究的系统阶数更高时,采用手动方式进行线性化计算更加不切实际。而采用MATLAB软件作为辅助计算工具,并通过编程实现线性化计算过程,不仅可以大大减少计算工作量,而且可以为后续分析工作提供诸多便利。
2.3.2 系统小干扰动态模型的验证
本文通过对比 MATLAB中小干扰动态模型的计算结果和 PSCAD中电磁暂态模型的仿真结果,来验证小干扰动态模型的正确性。事实上,小干扰动态模型的验证工作是融合在建模过程中的。图 4为在MATLAB中建立小干扰动态模型的程序框图。
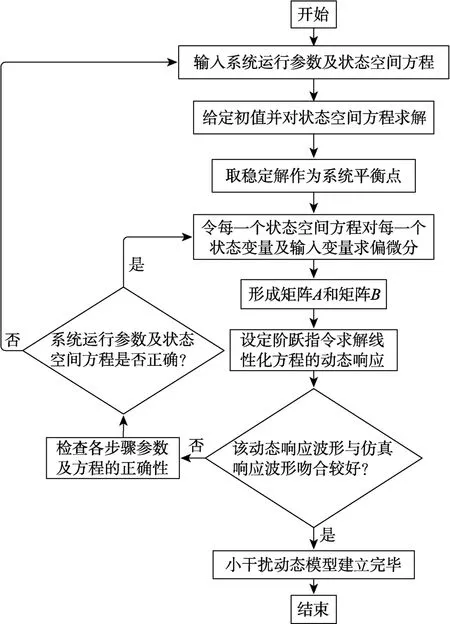
图4 建立小干扰动态模型的程序框图
现对图4中各主要步骤及其涉及到的编程函数作进一步说明。首先建立一个“脚本”文件用以列写系统运行参数、准稳态计算公式及状态空间方程,然后给定恰当的初始值,并使用ode45函数求解状态空间方程组的数值解;接着调用 diff(函数,变量名)完成偏微分计算步骤,生成矩阵A与矩阵B,即小干扰动态模型;再调用stepfun函数,令系统输入参数发生阶跃,以观察小干扰模型的动态响应;最后将PSCAD中的波形数据导入MATLAB,并将小干扰动态模型的阶跃响应波形与 PSCAD电磁暂态模型的阶跃响应波形进行对比,从而确定小干扰动态模型的建立是否准确。
下面简要叙述验证小干扰动态模型正确性的具体做法。系统初始时运行在表1所示的参数下,t=3 s时令直流电流指令值Idcref由1.0 pu下降阶跃至0.95 pu,1 s后恢复至初始运行状态。
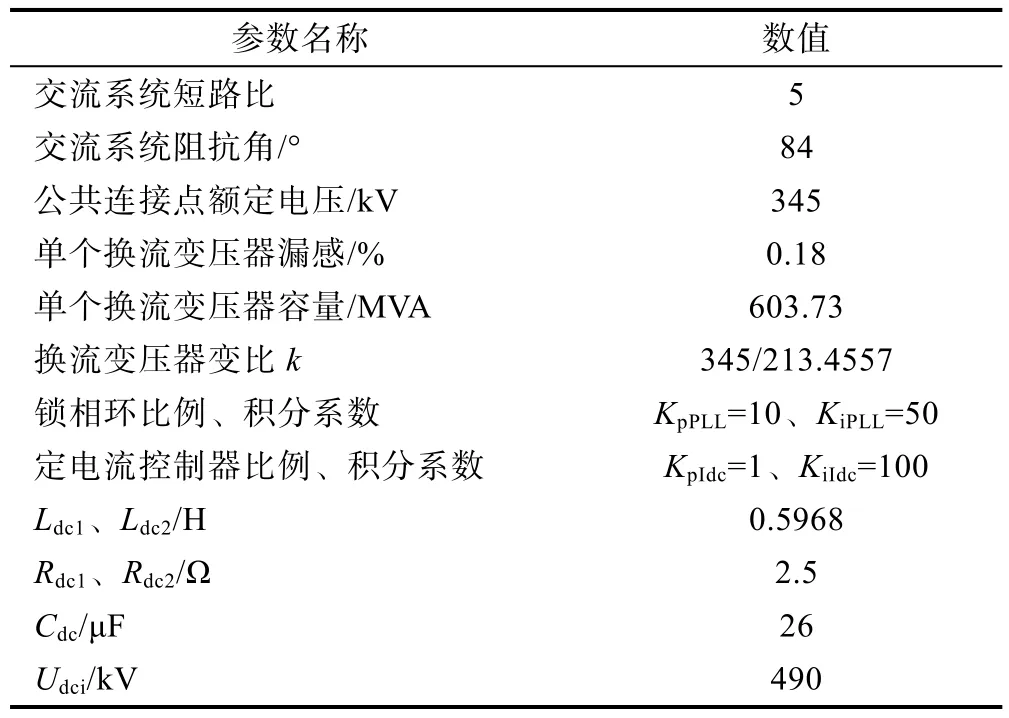
表1 系统初始运行参数
图5从公共连接点电压vPCC和锁相环输出频率f两个方面对比了MATLAB小干扰动态模型和PSCAD电磁暂态模型的仿真结果。
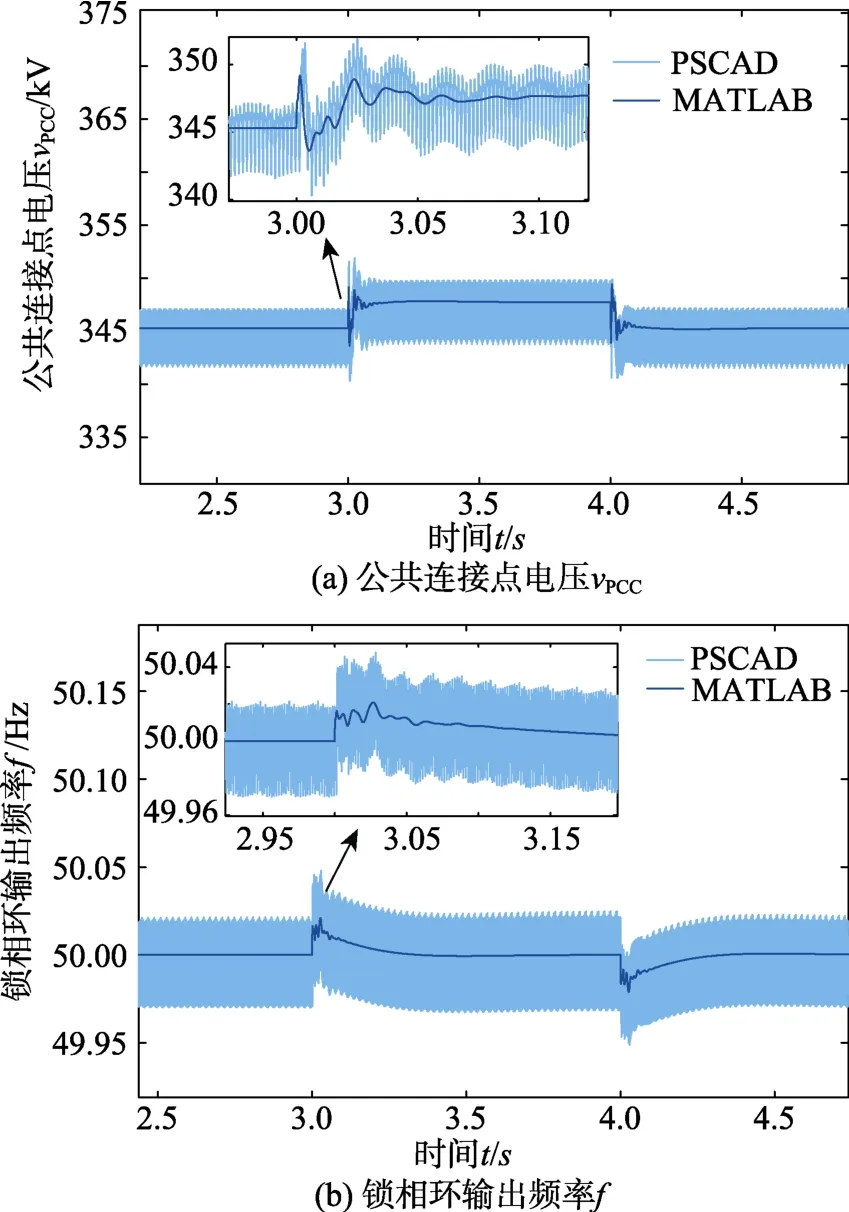
图5 直流电流指令值发生阶跃时的系统响应曲线
由图5可知,在直流电流指令值Idcref发生相同阶跃的情况下,MATLAB小干扰动态模型和PSACD电磁暂态模型的仿真结果基本一致,从而验证了本文所建立的小干扰动态模型的正确性。
2.4 小扰动稳定性分析仿真演示
从系统的状态方程来看,系统的稳定性取决于其线性化系数矩阵A的特征根。由李雅普诺夫第一法可知,系统唯一平衡状态是渐进稳定的充要条件,是矩阵A的所有特征根lA均具有负实部。当系统某一参数改变时,可通过在 MATLAB中绘制根轨迹的方法,来直观反映该参数对系统小扰动稳定性的影响。
现以定电流控制器比例系数KpIdc为例,保持系统其余参数同表1,仅令KpIdc由1逐渐变化至5,变化步长取为0.05。在此过程中,KpIdc的数值每发生一次变化,线性化系数矩阵A都随之发生一次改变,相应地矩阵A的特征根也发生改变。若将此变化过程中矩阵A所有的特征根绘制在一张图中,即可得到系统特征根在KpIdc由1变化至5时的轨迹,如图6所示。
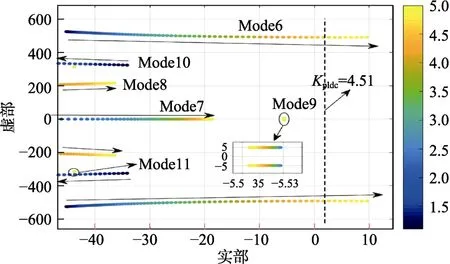
图6 KpIdc变化时矩阵A的根轨迹
由图6可知,当KpIdc由1逐渐增大时,主导模态(Mode6)对应的特征根逐渐向虚轴靠近,系统小扰动稳定性逐渐减弱。而当KpIdc>4.51时,矩阵A的特征根出现非负实部的情况,根据李雅普诺夫第一法,系统失去小扰动稳定性。为进一步验证小干扰动态模型的正确性,保证分析结果的可信度,在 PSCAD电磁暂态模型中令KpIdc在t=3 s时由1跃变至6,得到系统的整流侧直流电流动态响应特性如图7所示。
从图 7的波形数据可以看出,当 KpIdc=6时,PSCAD电磁暂态仿真模型已失去稳定,波形呈振荡发散状态,其振荡周期为TPSCAD=13.4 ms。而MATLAB小干扰动态模型在 KpIdc=6时主导模态特征根为26.992±i495.254,对应的振荡周期为 TMATLAB=12.7 ms。考虑到 PSCAD电磁暂态仿真模型系统的阻尼比本文建立的小干扰动态模型系统阻尼大,可以认为二者结果接近一致,从而证明了上述小扰动稳定性分析方法的正确性。
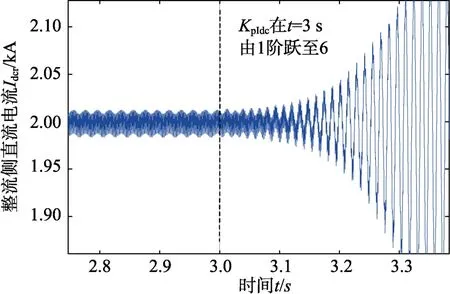
图7 KpIdc阶跃时直流电流动态响应特性
以上仿真方法有利于学生以此为参考,分析其他参数变化时系统的运行规律。
3 结语
本文利用 MATLAB软件搭建了高压直流输电系统数学模型,建立了相应的小干扰动态模型,并应用该模型对高压直流整流侧系统进行了小扰动稳定性分析。将本文介绍的小扰动分析方法应用在实际教学实践中,可对学生的学习有以下指导作用:
(1)通过将小干扰动态模型和电磁暂态分析相结合进行系统小扰动稳定性分析,可以弥补传统教学模式难以对高压直流输电系统直观展现数学分析方法的缺陷。通过在 MATLAB中建立小干扰动态模型来进行小扰动稳定性分析,可直观地展现系统参数改变对系统稳定性的影响,对提高课程教学质量和加深学生理解程度大有裨益。
(2)利用仿真软件易于实现复杂算法和绘制数据图形的优势,帮助学生快速理解并掌握课程知识的重点和难点,提高学习效率。
(3)通过搭建系统的数学模型、小干扰动态模型和电磁暂态模型,学生能够了解并熟悉当前编程、建模及仿真领域的主流软件,不仅有助于他们提高深入探索理论知识的能力,而且能拓宽应用实践技术的视野,从而培养创新实践能力。
(4)MATLB仿真实验教学方法可对传统电磁实验教学方式进行补充。其仿真结果可帮助学生更好地理解高压直流输电系统中各电气量的关系,有效避免所授知识的宽泛化和概念化。
