不同区域的土壤中硝态氮含量的反演模型

田安红，杨丽华，崔丽梅，付承彪，赵俊三，熊黑钢，于 龙

（1. 曲靖师范学院 信息工程学院，云南 曲靖 655011；2. 昆明理工大学 国土资源工程学院，云南 昆明 650093；3. 北京联合大学 应用文理学院，北京 100083；4. 曲靖师范学院 城市学院，云南 曲靖 655011）

土壤中硝态氮含量的准确估测是合理施用氮肥、确保农作物生长的关键[1]。高光谱遥感技术因具有快速、无损、实时、精度高等优点[2-3]，被广泛用来估测土壤中的养分信息。例如，单海斌等[4]以新疆农田灰漠土为研究对象，在暗室内测量土壤的高光谱，并对其进行倒数、对数和一阶微分变换，采用多元逐步方法预测有机质含量，结果显示，对数一阶微分后的反演模型精度最高，决定系数为 0.82。刘凡等[5]研究新疆干旱区灰漠土中全氮的高光谱特性，一阶微分后的土壤高光谱与全氮的相关性明显优越原始高光谱与全氮的相关性，一阶微分后建立的估测模型在验证集的决定系数达0.8，总体上预测模型的精度较高。张佳佳等[6]研究江西省赣州市稻田土壤的高光谱特性，并建立反演全磷和有效磷的预测模型，表明全磷的特征波段位于534 nm和1 090 nm，而有效磷的特征波段位于365 nm、1 631 nm和2 223 nm，通过SPSS软件建立的全磷和有效磷的多项式回归模型的相关分析误差分别为1.43和1.54。尤承增等[7]采集横山县的84个土壤样本，测量其在 350～2 500 nm波段的高光谱反射率曲线，并对原始高光谱进行一阶微分变换，根据极大相关性原则来筛选敏感波段，通过模糊识别理论来建立全钾的预测模型。以上的研究表明，利用高光谱遥感技术检测土壤中的养分是可行的，但主要涉及的养分为有机质、全氮、全磷、全钾等。而硝态氮的含量普遍在土壤中较低[1]，准确检测硝态氮的含量存在一定的困难。目前，针对土壤中硝态氮含量的高光谱反演研究报道非常少。

另外，现有文献针对土壤养分的反演主要是以被人类干扰过的土壤为研究区域，很少对比分析没有受到人类干扰的土壤和受到人类干扰的土壤。因此，本研究以新疆不同人类干扰区域的土壤为研究对象，采用非线性的 BP神经网络建立精确反演硝态氮含量的模型，为研究不同区域的土壤硝态氮反演提供了可靠的依据。

1 材料与方法

1.1 土壤样品采集

研究区域为新疆阜康的土壤，地理坐标如图1所示。2个不同研究区域主要是以不同人类干扰情况来划分。图1的右边定义为没有人类干扰的区域（A区），图1的左边定义为有人类干扰的区域（B区）。因为在A区和B区中间有一条长约15 km左右的大水渠，水渠基本隔断了人类在A区的日常活动，A区的土壤表层生长着如红柳、梭梭等耐盐性的植物。B区的土壤被当地居民犁地开发为人工林地等。

图1 研究区域

土壤样品的采集时间为2017年5月中旬，利用五点取样方法来采集表层土壤0～20 cm，A区和B区分别为25个和30个土壤样本。野外采集的样本密封保存后带回实验室，通过自然风干、去除残渣、研磨等处理后[8]，由中科院新疆生态与地理研究所的专业人员测量土壤中硝态氮含量。

1.2 测量土壤高光谱

土壤的高光谱反射率采用 ASD FieldSpec3来测量[9]，该光谱仪的全波段范围从350 nm到2 500 nm。野外高光谱的测量要选择晴朗无云无风的天气进行，时间选择在当地14:00左右进行。每次进行高光谱测量之前都需要白板校正操作，每个土壤样本点重复测量 10次，取其平均值代表该样本点的最终高光谱反射率。

1.3 数据处理与研究方法

为了减少测量过程中的噪声干扰，需要利用Savitzky-Golay平滑方法对测量的高光谱进行滤波处理。同时删除信噪比低的边缘波段范围的高光谱，即350～390 nm和2 401～2 500 nm。又因野外高光谱的测量还受到大气中水分的影响，因此还需要删除1 400 nm和1 900 nm附近的波段，即1 355～1 410 nm和1 820～1 942 nm。高光谱预处理后的曲线如图2所示。

本研究的建模方法采用线性的逐步多元回归模型（stepwise multiple linear regression，SMLR）和非线性的BP（back propagation）神经网络模型来实现。SMLR的主要思路是：考虑所有变量的方差贡献值[10-11]，按照其值大小的重要性进行筛选，逐步依次地选则进入回归方程中。基于误差反向传播算法的BP神经网络具有强大的非线性映射能力[12-13]，其主要由输入层、隐藏层和输出层组成。本研究在Matlab2019a中编程实现，设置的最大迭代次数设为 1 000，期望误差设为le-6，学习速率设为0.001，训练函数选择设为trainscg，隐藏层节点个数设置为 300。同时，SMLR和BP模型的训练土壤样本选择60%，测试土壤样本选择40%。

图2 土壤的高光谱反射率曲线

1.4 定量估算模型精度验证

本研究采用3个参数来评价预测模型的精度，即决定系数（R2），均方根误差（RMSE）和相对分析误差（RPD）[14-15]。当R2的值越接近1，RMSE的值越接近于0时，说明所建立的模型的预测精度越高[16]。并且当RPD值大于2.5时，说明所建立的模型的预测能力极强；当RPD值在2.0～2.5之间时，说明所建立的模型的预测能力很好；当RPD值在1.8～2.0之间时，说明所建立的模型的预测能力好；当 RPD值在 1.4～1.8之间时，说明所建立的模型的预测能力一般；当RPD值在 1.0～1.4之间时，说明所建立的模型的预测能力很差；当RPD值小于1.0时，说明所建立的模型不具有预测能力。

2 仿真结果与讨论

2.1 土壤高光谱与硝态氮含量的相关性分析

因土壤的原始高光谱与硝态氮含量的最大相关系数，在A区为0.322 361，在B区为0.439 667，总体来说，A区和B区的最大相关系数值较低，难以选择出敏感波段。因此，进一步将土壤的原始高光谱进行一阶导数和二阶导数变换（见图3），发现变换后的高光谱与硝态氮的相关系数被明显地增大，A区一阶导数与硝态氮的最大相关系数绝对值为0.695 314，对应波段为142 8 nm，A区二阶导数与硝态氮的最大相关系数绝对值为0.718 687，对应波段为681 nm；B区一阶导数与硝态氮的最大相关系数绝对值为0.696 547，对应波段为1 526 nm，B区二阶导数与硝态氮的最大相关系数绝对值为0.638 911，对应波段为2 252 nm。在图3中，仅有部分波段通过了0.01检验（见表1），可选取通过0.01检验的波段作为后续反演模型的敏感波段。由表2可知，A区一阶导数和二阶导数通过0.01检验的波段分别为61和33个；B区一阶导数和二阶导数通过0.01检验的波段分别为95和33个。

2.2 硝态氮定量估测模型精度比较

将表1中通过0.01检验的波段对应的高光谱反射率作为自变量，将土壤的硝态氮含量作为因变量，建立 BP神经网络模型和逐步多元线性回归模型估算硝态氮含量（见表2）。SMLR一阶导数模型的相对分析误差RPD很低，在A区的RPD值为1.132，在B区的RPD值为1.146；SMLR二阶导数模型的相对分析误差RPD也很低，在A区的RPD值为1.183，在B区的RPD值为1.014，说明SMLR一阶导数和二阶导数模型都无法预测土壤硝态氮含量。

一阶导数后的BP神经网络模型在A区的RPD值为2.884，R2为0.874，RMSE为18.980，因RPD值大于2.5，说明该模型对硝态氮含量的预测能力很强。二阶导数后的 BP神经网络模型在 A区的 RPD值为2.317，R2为 0.807，RMSE为 24.142，因 RPD 值在2.0～2.5之间，说明该模型对硝态氮含量的预测能力好。一阶导数后的BP神经网络模型在B区的RPD值为2.226，R2为0.929，RMSE为26.959，因RPD值在2.0～2.5之间，说明该模型对硝态氮含量的预测能力好。二阶导数后的 BP神经网络模型在 B区的RPD值为1.956，R2为0.887，RMSE为29.922，因RPD值在1.8与2.0之间，说明该模型对硝态氮含量的预测能力较好。

图3 土壤高光谱与硝态氮的相关系数

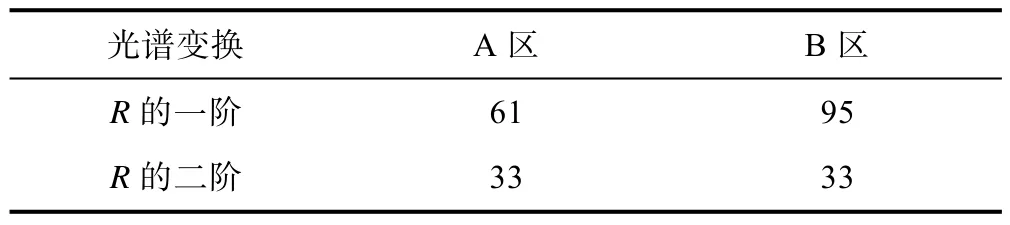
表1 通过0.01检验的波段

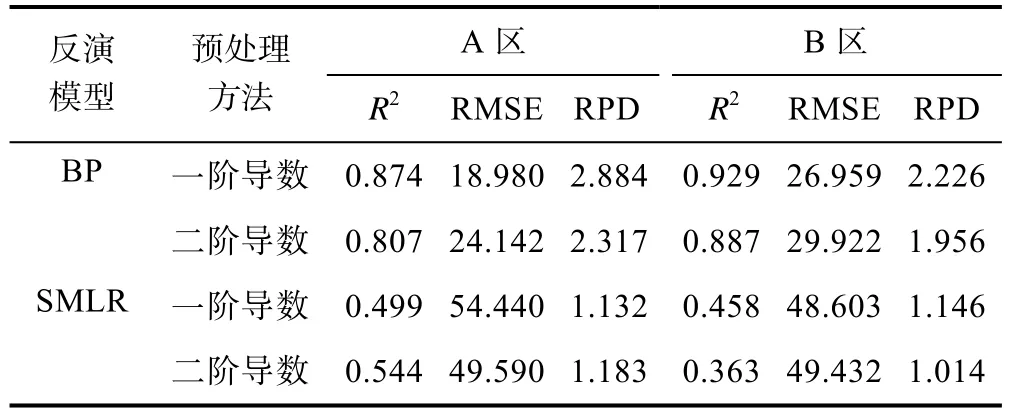
表2 BP和SMLR的建模精度比较

利用验证集的检验样本对SMLR和BP模型进行检验，SMLR和BP对硝态氮含量的真实值与预测值的比较如图4所示。SMLR一阶导数和二阶导数的样本值比较分散，拟合线偏离 1∶1线的程度较大。BP一阶导数和二阶导数的样本值基本集中分布在 1∶1线附近。BP一阶导数在A区的拟合方程为y=0.931 62x+0.672 57，在B区的拟合方程为y=0.781 97x+5.646 8。BP二阶导数在 A区的拟合方程为 y=0.888 86x+6.699 8，在B区的拟合方程为y=0.699 68x+26.735 4。图5为BP神经网络的训练结果。BP模型的隐藏层节点数都设置为300个，输出层1个变量。输入变量在A区一阶导数、B区一阶导数、A区二阶导数、B区二阶导数中，分别对应61个、95个、33个、33个波段的高光谱反射率。并且A区一阶导数、B区一阶导数、A区二阶导数、B区二阶导数分别进行迭代13次、12次、40次、8次满足精度要求。

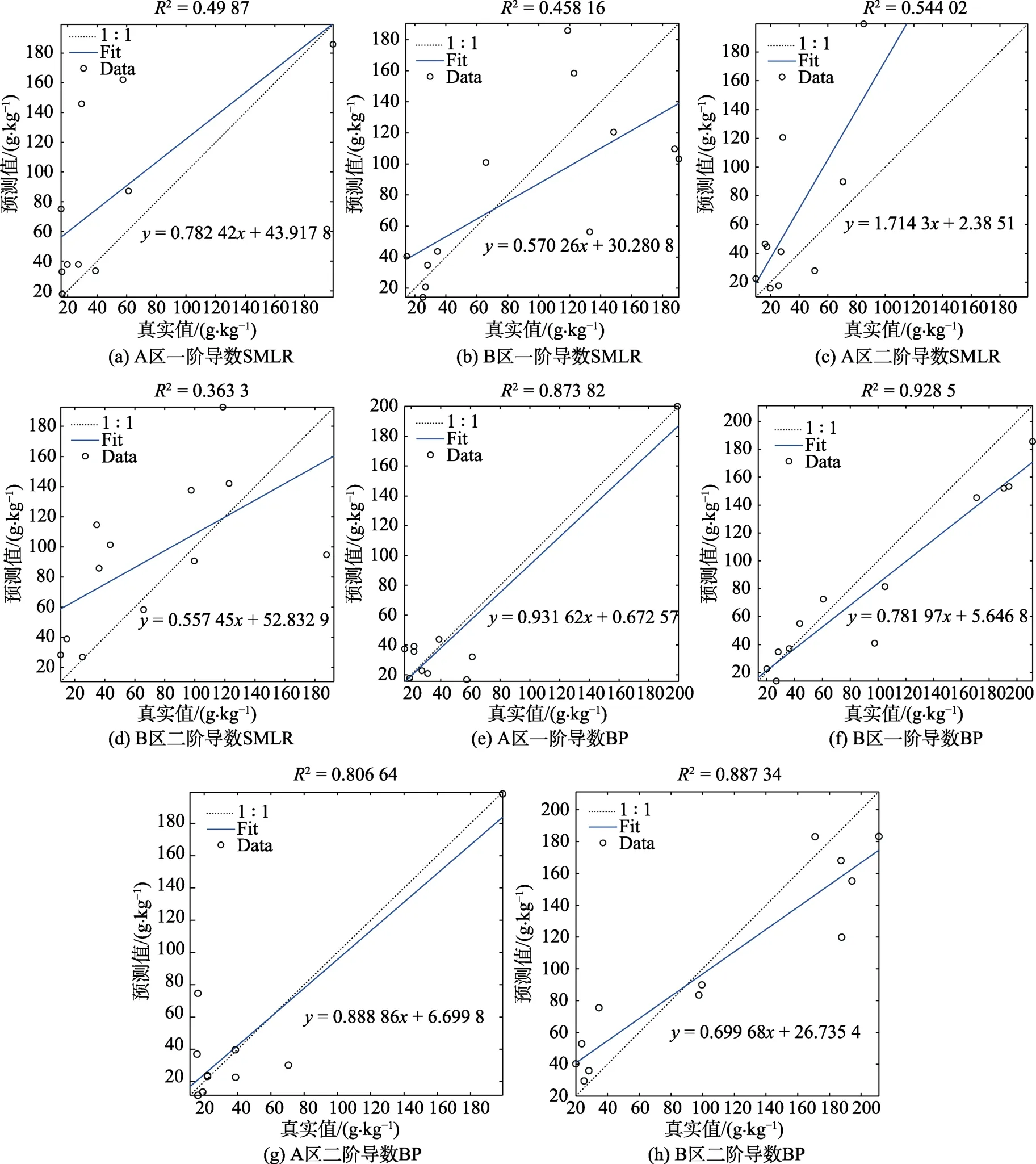
图4 SMLR和BP对硝态氮含量的真实值与预测值的比较

图5 BP神经网络训练

3 结语

原始高光谱的一阶导数和二阶导数通过0.01检验的波段数量，在A区分别61个和95个，在B区均为33个。一阶导数变换后的BP神经网络模型的预测精度最高，在A区的RPD为2.884，R2为0.874，RMSE为18.980，该模型对硝态氮含量的预测能力很强；在B区的RPD为2.226，R2为0.929，RMSE为26.959，该模型对硝态氮含量的预测能力好。二阶导数变换后的BP神经网络模型在A区的RPD值为2.317，R2为0.807，RMSE为24.142，该模型对硝态氮含量的预测能力好。二阶导数变换后的BP神经网络模型在B区的RPD值为1.956，R2为0.887，RMSE为29.922，该模型对硝态氮含量的预测能力较好。一阶导数和二阶导数变换后的SMLR模型的RPD值很低，基本在1.1左右，说明其对2种土壤中的硝态氮含量的预测能力非常差。