基于多因素模糊推理的卫星综合效能评估
2020-09-26虞业泺郑倩云杨善强方小梅
虞业泺,郑倩云,杨善强,常 枭,方小梅
(1.中国科学院微小卫星创新研究院,上海 201210;2.上海微小卫星工程中心,上海 201210;3.中国科学技术大学,合肥 230000)
0 引言
随着卫星系统的快速发展,各类卫星迅速出现。各国都建立了卫星网络覆盖,无论从军事还是商业角度,卫星实力的强弱很大程度上相关于国家实力的盛衰[1-2]。在如此众多的卫星建设需求下,对卫星的综合效能评估也显得越来越重要。较之之前的单任务、单卫星、单一化的卫星任务实现,现如今的发展趋势已经向多任务、灵活机动、多卫星、集群化的卫星任务需求进行转变[3-4]。因此原有的对卫星综合效能评估的性能穷举法及单性能评估法都已经无法顺应并满足当下的卫星任务[5-6]。
面对现实需求,需要对原有的针对卫星复杂系统所进行的综合效能评估方法进行适当的更新,以此来适应现如今灵活、机动、可变、多任务的复杂卫星需求。
1 卫星综合效能评估指标体系
卫星综合效能评估指标体系通常用于直观、层次化的反应卫星实际任务需求、功能实现方式及内部功能划分关系。其层级划分方式一般可以分为:卫星系统综合效能层、卫星任务指标层及卫星能力实现层[7-8]。
卫星综合效能层通常定义卫星总体综合效能、卫星实际属性及待综合评估卫星实际状态,如遥感类、导航类、通信类卫星综合效能、微纳集群卫星综合效能或导航星座卫星综合效能等。
卫星任务指标层则通过对卫星综合系统进行明确后的任务大项划分,以微纳集群卫星为例,如图1所示。包含导航任务、通信任务、遥感任务等。为了满足上述任务指标,需要对该指标进行细化,针对导航任务其能力实现层应包含:导航定位精度、导航服务时间、导航覆盖范围、空间信号传输等能力[9-10];而遥感任务能力层则包含:光学成像侦查能力、雷达成像侦查能力、电子情报侦查能力等[11-13];通信任务能力实现层包含:用户容量、通信速率、抗干扰性等能力指标数据[14-15]。

图1 微纳集群卫星综合效能评估指标体系层次
2 卫星系统综合效能评估方法研究
2.1 卫星综合效能评估一般流程
目前对卫星的综合效能评估一般流程为针对卫星复杂大系统建立评价指标体系;后采用层次分析法确立评价指标的权重;定义评价结果的备择集;后根据模糊理论计算单因素评判矩阵;最后通过综合评判从而确定系统综合效能。其具体流程如图2所示。

图2 卫星综合效能评估流程
目前多通过对每个单一指标项进行模糊隶属度函数类型实现,并在实现过程中对每一个指标都需介入专家经验系统,通过向专家咨询隶属函数参数获得对应的取值后,然后根据对应的取值来计算所有定量指标相对于备选择单项指标元素的模糊向量,再以这些模糊向量为行来构造性能层因素的单因素评判矩阵R,在得到该单因素评判矩阵后使其与所判层的任务指标权重向量A进行矩阵运算,所得到的结果即认其为对该卫星的效能评估指标体系下的满意度隶属向量矩阵B(当前为单层次下的考量,若为多层次则需引入层次分析法,将所得的满意度隶属向量矩阵B作为上一层次的单因素评判矩阵R再进行矩阵计算,依次类推至最高层次)。根据最大隶属度法则,可以认为卫星系统的综合效能满足度评估为满意度隶属向量矩阵B下隶属度最大项。选取其最大项作为卫星系统综合效能评估值。
综合考虑上述实现方式,不难发现在对每个单一指标进行模糊隶属度函数确定方法虽然多样,但基本上无法脱离专家经验系统。过多的使用专家经验系统能够很好的对系统任务及需求导向等大方向进行把控,且对应不同的任务需求提出有价值的指标划分方式。但同样其也面对以下三方面问题。
1)能动性:从需求的分解到指标体系的划分再到单一指标项的模糊隶属度的确定很大程度上都依赖专家经验系统,专家经验及大量工程师的指导意见固然重要,但面向不同任务,其需求都不尽相同。对于类似任务需求而言指标体系的确认和模糊隶属度的确认相对于最后的综合效能评估值而言,同一指标项可能会随着类似任务需求的变化而发生权重变化,而对于类似任务专家经验系统由于其受限于样本库及专项专家模型库规模而很难对精确的小点进行修正,也就是说无法对相似度较高的任务需求下的同一指标项进行一定程度下的小范围精确修正。
2)主观性:随着专家经验系统的引入程度的提升,往往会对评估指标体系产生较大的主观影响,虽然专家的个人因素对评估体系产生的主观性影响可以通过增加专家数量的方式进行减轻,但一味的增加专家数量显得并不可取,且通过人数增加来减轻主观评判色彩的效率的增效比也十分的低。
3)单一性:当前所采用的几乎都是对所确定的每个单一指标向量进行定量的模糊隶属度函数确定,该隶属度函数取值确定来源与专家咨询,并以此作为计算矩阵基础用于层次矩阵计算。但分别对单一指标项进行定量确定,往往存在较大的不可行性,如针对两个任务需求差异较小,但就某几方面存在差异的任务需求,若都是对单一指标单独定量化往往无法体现这些差异,且容易忽视差异性,从而增加风险。
2.2 多因素模糊推理评估效能
本文提出了一种新的计算方法用于卫星综合效能评估的实现,通过改进模糊推理评判法,在原有只对单个评估指标进行考量的情况下,创新的加入指标间的多因素考量并与层次分析法相结合的方式对卫星综合效能评估指标提出了一种新的解法。模糊推理算法是当下运用于卫星效能评估的重要手段。
由于卫星综合评估指标体系的评判并不是非‘0’即‘1’的存在,很多情况下该指标体系是以一种不确定度的形式出现,因此通过以一般集合论为基础描述工具进行数理逻辑扩展,将模糊因素引入评价指标集就显得合理贴切。整个评估实现流程都是以单个评估指标的评估结果为基础,同时由于卫星系统的效能评估存在鲜明的层次性,因此对每个评价指标都需要由底下一层的若干评价指标来决定。整个效能评估流程是一个自底向上的过程。以两级评估模型为例介绍多因素模糊推理及层次分析法的基本流程,总体流程框图如图3所示。

图3 基于多因素模糊推理的卫星综合效能评估
1)评估模型等级划分:
以任务需求为导向对卫星综合效能指标层次进行梳理划分,如对该评估模型划分为两级评估模型,其层次关系自底向上为:实现层L1、任务层L2。

图4 卫星综合效能评估模型等级划分
2)评价指标体系梳理:
完成层次划分后,需要对满足实际任务需求下的卫星效能指标按层次进行评估指标体系梳理。本文中,针对实现层L2进行评估指标体系建立,该层级下包含的评估指标体系包含:L2={L21、L22、L23…L2n};其上层次任务层L1同样进行指标体系分解梳理:L1={L11、L12、L13…L1n}。得到总体指标集为各分指标集的集合即L=L1∪L2。
3)评价指标权重确立:
考虑到卫星综合效能指标体系评估往往需涉及多个评估指标项,同时各指标项及评估体系层次架构多重化,一般的定性或定量分析技术很难对评价指标权重进行权值划分。因此本文将利用层次分析法将卫星综合效能指标体系进行定性和定量相结合的方式进行系统分析。结合上述评估模型等级划分,该方法的运用能够将复杂、多样化的卫星综合效能评估指标体系进行有序的层次递进,同时将指标体系按照同层两两相较比对从而将定性权重指标量化形成具有实际定量衡量能力的数据,该相对数据即是整个卫星综合效能指标的权重。通过量化后的指标权重按照层级以各自不同的权重值划分,则第一层评价指标体系的权重向量为W1={a1,a2,…,an},第二层评价指标体系的权重向量矩阵则为W2={W21,W22,…,W2n},其中W2i={ai1,ai2,…,ain}(i=1,2,…,n)。
4)单因素评价结果集合建立:
将来自专家或经验系统所得的考量结果与实际语言评判类模糊概念相结合,针对某一特定指标或事物项选取可能的评价结果,若评价结果包含{很好、好、一般、较差、差}共5个结果,则所建立的评价结果集合V相对应的为V={a1,a2,a3,a4,a5},其中a1,a2,a3,a4,a5分别对应评价结果中的很好至差评判标准。
5)单因素指标评判矩阵确立:

6)多因素评价模糊隶属度集合建立:
相较之单因素评价结果集合所建立的模糊隶属度集合,多因素评价结果集合选取单一结果输出,以两两相较为比对结果为{优、等同、劣}为评判标准建立集合,但只选取最终高概率结果项,最终建立集合为Z2k={zk1,zk2,…,zkn}。
7)多因素模糊隶属度加权指标建立:
当前几乎所有的效能指标评估都基于如上所述的层次分析结合模糊理论实现,且通常只对单因素指标引入专家经验系统进行模糊隶属度确认并用于层级计算,但正如前文所述,对单因素指标进行模糊隶属度确认并将其与指标体系权重作为效能评估的唯二计算因子容易过度引入专家影响且同时相对较少的考虑多因素下的各指标体系间的关系,其次对于后期效能评估的迭代回馈作用也较不明显。
针对以上诸多不足,本文在单因素指标评判基础上提出了一种多因素模糊隶属度加权指标,该指标在已进行相关单因素指标建立模糊隶属度的基础上,加入多因素模糊隶属度加权指标Q,该指标的建立需考虑同层级间各单指标之间的相关性。同样以第二层级为例,多因素模糊隶属度指标为:
D2={D21,D22,…,D2j}(j=1,2,…,n)
该指标的建立需先对该层级各指标进行拓扑罗列,假设第二层级具有3个单因素指标为例,其拓扑矩阵罗列如表1所示,该矩阵的获得首先以单指标因素为行进行排列,在利用前述所提出建立的多因素评价模糊隶属度集合,以D21为首轮比较数据,将其分别于同层级另外两个单因素指标D22、D23进行比对,得到相对大值。同时计算其相对概率结果作为该两两相较下的输出结果,待结果获取后将其按照从大到小进行排序,获取并建立的多因素评价模糊隶属度集合D2={D21,D22,D23}(D21>D22>D23)。

表1 多因素隶属度指标比较
待结合多因素评价模糊隶属度获取后还需要确立加权指标项,通过对同层次各单因素之间的两两相较过程后的多因素评价模糊隶属度集合D2进行加权判断,以来自专家经验系统的量化加权综合系数为最终相对加权总量进行逐项分配。以10%作为本层级量化加权综合系数,在多因素评价模糊隶属度集合基础上获得的多因素模糊隶属度量化加权指标Q2={0.05(D21),0.00(D22),-0.05(D23)}。
8)综合层级评判:
当前级的初级综合评判结果N来自当前层级的权重矩阵W与单因素评判矩阵R的乘积,同时通过多因素模糊隶属度量化加权指标值Q的获取,并将所获取的量化加权指标Q对对应单因素指标评判矩阵最优位进行加权,同时在最劣位减去最劣加权值,最终的当前层级评判结果N*=W×(R+“Q”)。且当前层级的评估结果N作为上一层同样计算的权重矩阵W。如此层层运算至最高层级获取最终评判结果Nfin。
9)综合评判结果确认:
综合效能评估最终的结果获取依赖于利用模糊推理理论结合专家经验系统,将模糊指标进行定量化,并将定量化的指标通过上述方法进行定量值求解获取,针对卫星系统,其最终待评价系统相对单一,因此可以直接采用模糊分布法,直接将最后的结果看做最终评判结果。
10)效能结果迭代:
单纯的效能评估值计算无法满足瞬息万变的实际需求,同时无法满足对纷繁杂乱的军事实际需求及战场态势响应。一个指标不再足以代表一类卫星系统,因此需要对具体任务背景下的卫星系统进行效能结果迭代,对不同的任务需求进行多因素评估模糊隶属度指标及权重矩阵微调来重新计算,得益于多因素评估模糊隶属度及加权指标的动态可调性,能够适应快速效能结果迭代计算,以任务满足度为导向迅速获取最终的效能结果。
3 效能评估仿真算例实现
综上,本文以就多因素模糊推理及层次分析法应用于卫星综合效能评估技术之上,以实际导航卫星综合效能评估为目标按照前述进行算例实现。
1)划分评估模型等级:
结合导航实际任务需求,进行导航卫星综合效能评估模型建立,建立该卫星简化效能评估指标体系模型如图5所示。
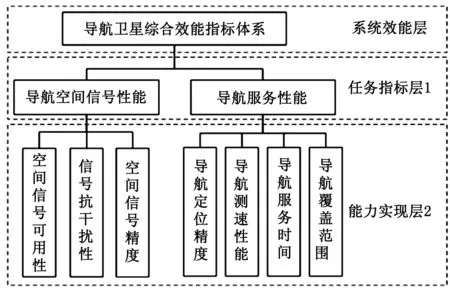
图5 导航卫星综合效能指标体系简化图
2)梳理评价指标体系:
针对任务层L1进行指标体系分解梳理如下。
L1={导航空间信号性能、导航服务性能};同理,对实现层L2建立评估指标体系为:L2={空间信号可用性、空间抗干扰性、空间信号精度、导航定位精度、导航测速性能、导航服务时间、导航覆盖范围}。于是总体指标集为L=L1∪L2。
3)确立评价指标权重:
针对已建立的导航卫星效能评估指标体系模型,利用层次分析法,并引入专家经验系统进行量化明确,所得的各层级指标的权重向量对应为任务层指标权重矩阵W1及实现层指标权重矩阵W2。其具体值,分别见表2、表3所示。

表2 任务层权重向量划分

表3 实现层权重向量划分
4)建立单因素评价结果集合:
选取{很好、好、一般、较差、差}为模糊综合评判内容,对应确立单因素评价结果集合V={a1,a2,a3,a4,a5},其中a1,a2,a3,a4,a5分别对应评价结果中的很好到差评判标准。
5)确立单因素指标评判矩阵:
然后单因素指标评判矩阵确立需要以层次化的方式对已梳理的评估指标体系进行从下至上的单因素评判,所有层级内的单因素实现量化指标都需要向专家经验系统进行咨询确认后得到,本例对系统能力层模糊向量的单因素评判矩阵向量R2如表4所示。

表4 单因素评判矩阵R2
同时以当前层模糊向量隶属度为行构造上一级评价指标评判矩阵R1=R2×W2。
6)确立多因素评价模糊隶属度集合:
在已进行相关单因素指标建立模糊隶属度的基础上,加入多因素模糊隶属度加权指标Q,对该层级各指标进行拓扑罗列后进行各指标间的两两相较过程后同样根据专家经验系统获得对多因素评价模糊隶属度集合D2={R24,R22,R27,R21,R25,R23,R26},以来自专家经验系统的量化加权综合系数为最终相对加权总量进行逐项分配。
7)建立多因素模糊隶属度加权指标:
以10%作为本层级量化加权综合系数,在多因素评价模糊隶属度集合基础上获得的多因素模糊隶属度量化加权指标Q={0.03(R24),0.02(R22),0.01(R27),0.00(R21),-0.01(R25),-0.02(R23),-0.03(R26)}。
8)评判综合层级:
当前层级评判结果N=W×(R+“Q”)。且当前层级的评估结果N作为上一层同样计算的权重矩阵W。如上所示计算得到N1(R1)如表5所示,得到同样根据实现层计算方式得到最终的B=R1×W1。通过如此层层运算至最高层级获取最终评判结果Nfin={0.201,0.411,0.138,0,0}。

表5 任务层单因素矩阵
9)综合评判结果确认:
根据卫星系统的特点,对评判结果采用模糊分布法,选取最后结果中的最大值看做最终评判结果。如上例分析最终评判结果为:其最终的评判标准依据为最大评判隶属度项为41.1%的专家计算结果认为该效能评价计算结果为“好”。
考虑到所使用的例子为简化后的导航卫星综合效能评估,其计算结果只能作为一个考察参考点,更详细准确的参考点仍然需要通过对导航卫星任务满足度出发,同时兼顾经济成本、风险等要素并结合实际使用场景、任务实际支撑等个方面出发,对评价指标体系进行微调同时对单因素指标评判矩阵及多因素模糊隶属度加权指标进行专家经验量化输出及数学计算得到最终满足实际、贴近真实的卫星综合效能评估值,使其可以真正做到对整个卫星系统甚至多卫星集群乃至星座的综合效能的真实评估反应,为卫星实现形成一定的保障评估价值。
4 结束语
卫星系统作为国防力量的有力保障、科技水平的高度集成体现,几乎被世界上所有国家作为重点发展方向。同时针对卫星预研、设计、实现、列装、发射再到运维每一个环节都需要耗费巨大的人力物力成本。如何去实现对预研卫星系统、在研卫星系统及实际运行卫星系统进行综合效能评估显得尤为重要,因此一套好的卫星综合效能评估方法能够参与到整个卫星全流程中来,能够为卫星总体的效能指标进行优选及显示指标设计评估。虽然该多因素模糊推理及层次分析法的实现不一定能100%反应真实卫星综合效能,但该方法的提出是对传统方法的一种大胆的创新,具有一定的新意及实际使用价值。
