基于变分贝叶斯算法的青霉素发酵过程建模
2020-09-26蔡子君杨慧中
蔡子君,谢 莉,杨慧中
(江南大学 轻工过程先进控制教育部重点实验室,江苏 无锡 214122)
0 引言
抗生素是一类生物产生的具有抑制某些细胞生长的次级代谢产物[1],其对于某些病原微生物的抑制和灭杀作用使其成为一种重要的药物。作为一种典型的抗生素,青霉素发酵过程具有以下特点:
1)时变性。发酵过程中青霉素的浓度取决于生成青霉素的菌丝浓度,而影响菌丝生长的因素众多,例如发酵罐中糖浓度、溶解氧浓度、pH值、温度等,并且这些变量都会随着时间改变,导致青霉素的发酵过程呈现很强的时变性。
2)非线性。青霉素是一种次级代谢产物,生成青霉素所需的众多基质、前体、以及副产物之间会发生复杂的反应,形成了一个多输入多输出的非线性系统,加大了青霉素的浓度预测难度。
3)阶段性。青霉素发酵通常经历4个阶段,分别为准备期、对数生长期、平稳期和消亡期[2],如图1所示,准备期中菌丝慢慢生成,青霉素主要在对数生长期生成,经过平稳期后菌丝逐渐水解,进入消亡期。
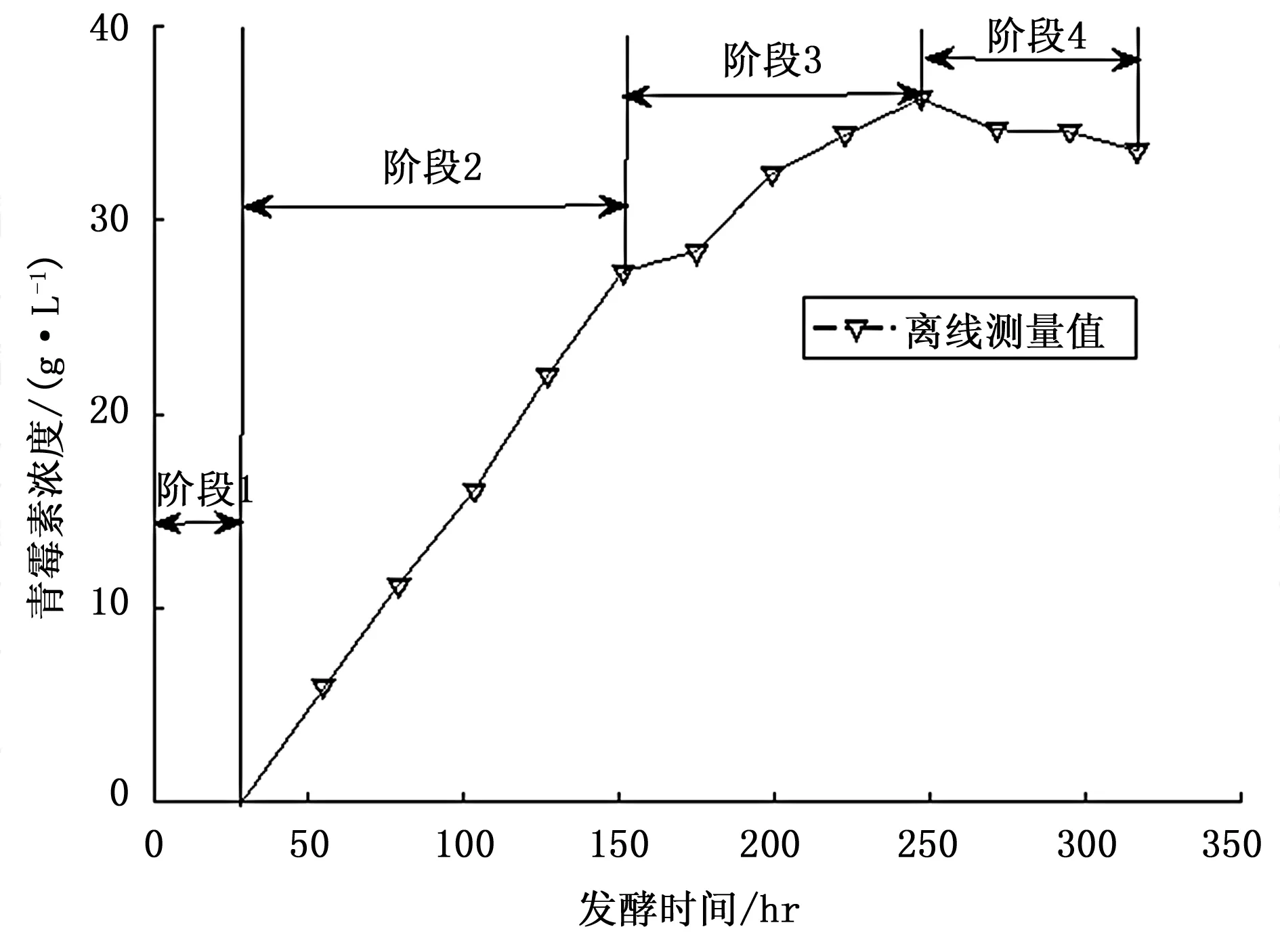
图1 青霉素浓度曲线阶段图
4)测量难度大。许多关键变量无法在线测量,需要进行离线分析,例如青霉素浓度、氮浓度、浓稠度等,导致关键变量的数据稀缺。
上述特点使得对青霉素发酵过程的预测和控制较为困难。过去提出的各种青霉素发酵过程的预测模型大致可以分为机理模型和数据驱动模型两类。最著名的机理模型是由Birol于2002年改进的非结构模型[3]。由于青霉素化学结构复杂,发酵过程涉及的反应众多,大部分机理模型不对内部结构讨论[4],而是对青霉素与菌丝的不同部分之间的动态关系进行描述。这种非结构模型能够一定程度上描述反应过程并在特定参数环境下模拟发酵过程,但是在面对实际发酵过程多变的环境时就显露出适应性差的缺点。近年来,许多基于数据驱动的青霉素发酵模型被提出,利用诸如神经网络、支持向量机等方法模拟青霉素发酵过程[5]。相对机理模型,数据驱动模型具有以下两点优势:1)不需要复杂的发酵机理知识,降低了建模难度;2)在发酵环境改变时不需要大量实验重新确定模型参数,降低了模型的维护成本。但现有的数据驱动模型大多利用Pensim仿真平台产生的数据,只能描述出在实验室规模下青霉素发酵的大致过程。
本文针对实际工业中的青霉素发酵过程,基于变分贝斯算法建立FIR融合模型。在模型选择方面,由于青霉素发酵过程具有明显的阶段性[6],本文采用多模型融合的思路,选取能够反应阶段特征的关键过程变量作为调度变量进行阶段划分,确定几个典型工况点以计算各局部模型的权重。工业青霉素发酵过程中生产环境复杂性使得过程存在着不确定性,这对发酵过程的辨识造成了很大的困难[7]。不确定性在工业过程辨识中的处理方法可分为两种[8],一种是通过不同模型的变化体现系统的不确定性;而本文采用的是第二种,即在模型结构已知的条件下,将系统不确定性通过模型参数的不确定性来体现。本文采用变分贝叶斯算法作为辨识算法,它是期望最大化(EM)算法在贝叶斯方法上的一种推广,相较于EM算法的点估计,变分贝叶斯算法可以估计参数和隐变量的整个后验概率分布,能够更好地描述青霉素发酵过程的不确定性。
1 青霉素发酵阶段划分
调度变量是指可以反应系统工作状态与阶段特征并能够人为调控的过程变量[9]。在Pensim仿真平台的环境下,冷水流加速率能比较好的反映发酵的阶段特征,所以在以往的青霉素发酵模型中经常被作为模型的调度变量。但是,在实际工业过程中,操作人员会频繁地改变冷水流加速率以保持稳定的发酵罐温度,导致实际过程中冷水流加速率(图2)不宜作为过程的调度变量。
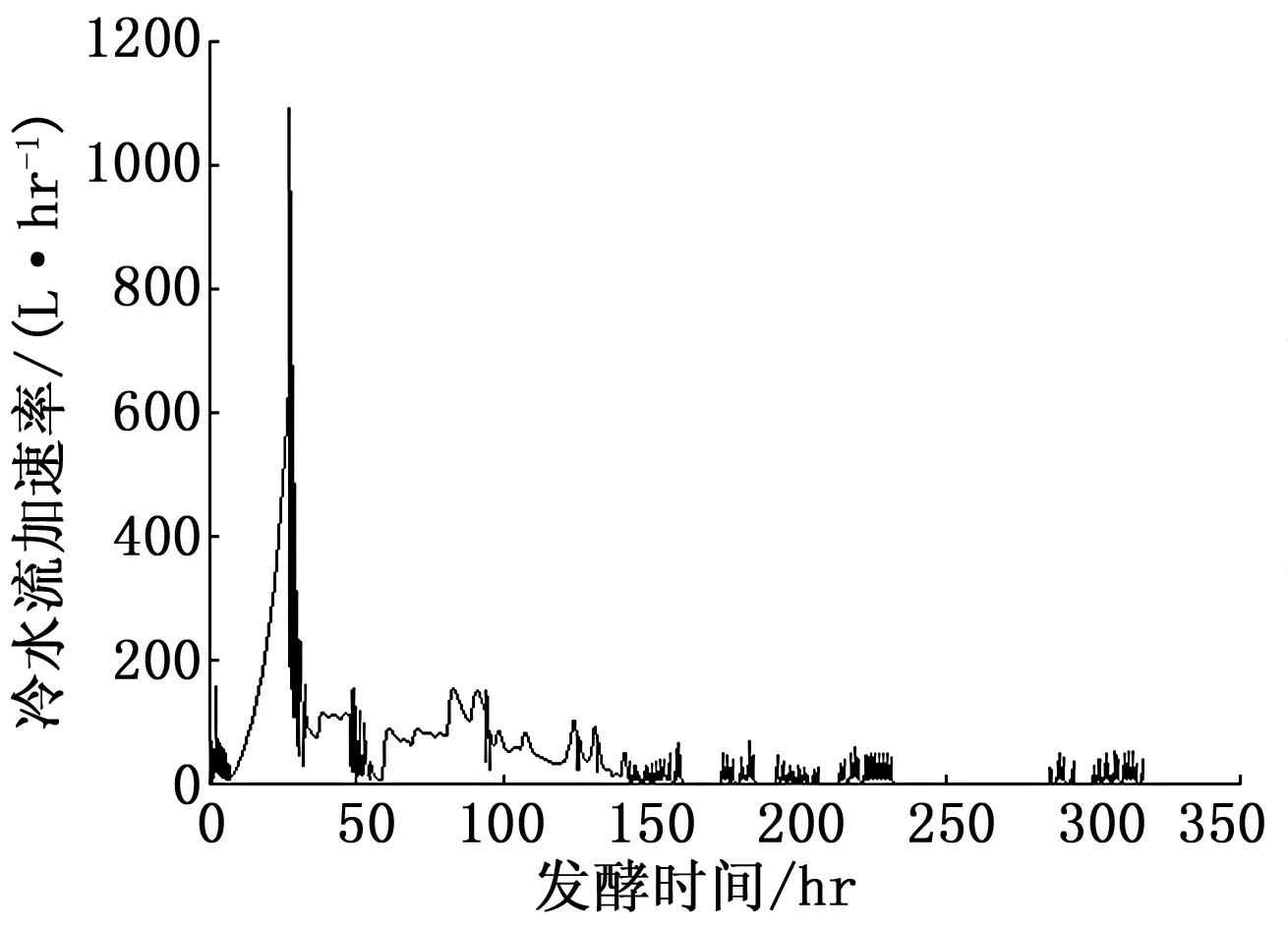
图2 工业环境下冷水流加速率图
考虑实际工业过程的操作环境,本文将使用葡萄糖流加速率作为调度变量。葡萄糖是青霉素发酵中底物的一种,其流加速率虽然在发酵过程中经过人为调整,但调整频率相对较低并且整体曲线能够体现发酵过程的阶段特性[10]。
为划分发酵过程的各个阶段,需要进一步对调度变量进行聚类。本文采用模糊C均值(Fuzzy C-Means,FCM)聚类方法[11]对葡萄糖流加速率进行聚类,并将各聚类中心作为发酵过程的典型工作点。FCM是一种基于目标函数的聚类算法,首先对聚类中心设置初值,然后通过最小化数据点与各聚类中心的距离和模糊隶属度的加权和为目标,不断修正聚类中心和分类矩阵直到符合终止准则,将具有类似特征的数据聚为一类。
在青霉素发酵过程的准备期中,菌体快速生长消耗氧气,当溶解氧水平下降到一定程度时,菌体会产生中间代谢物并开始生成青霉素[12],所以本文假定在准备期中青霉素浓度为零,而对数生长期、平稳期和消亡期这3个阶段分别对应3个不同的工作点。因此,在采用FCM算法对实际工业青霉素发酵过程中的葡萄糖流加速率进行聚类时,将聚类中心个数设置为3,相应的聚类结果如图3所示,其中三角形表示计算得到的聚类中心。
2 模型结构:FIR融合模型
考虑到在工业现场青霉素浓度为慢速采样[13],无法用于模型输入,所以本文采用FIR模型作为局部模型,然后通过权重函数将3个局部模型融合为全局模型来描述青霉素发酵的动态特性。局部FIR模型结构如下:
(1)
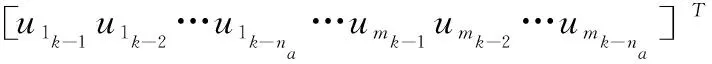
(2)
其中:k=1,2…N表示发酵过程的各时刻,输出变量yk为k时刻发酵罐中青霉素浓度,Ik=1, 2, 3表示k时刻变量隶属的局部模型,模型选择的输入变量个数为m,输入阶数设为na,ek是均值为0方差为σi-1(未知的待辨识参数)的高斯分布噪声,下标i=Ik表示各个局部模型。
采用高斯分布作为权重函数[14]:
(3)
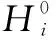
(4)
若各个局部模型的有效宽度Oi已知,根据式(3)~(4)计算出各子模型的权重后,容易得到系统全局模型的预测输出:
(5)
然而,局部模型的有效宽度Oi未知,需要与各子模型的参数θi以及噪声方差σi-1同时辨识,增加了系统辨识的难度。此外,考虑到实际过程的不确定性,本文通过引入参数不确定性,在VB算法框架下推导相应的辨识算法。
3 基于VB算法的模型参数辨识
3.1 VB算法回顾
令模型的参数集为Θ,隐变量集为Cmis,观测数据集为Cobs。对于存在未知参数的模型,边缘似然函数可以由下式计算:
(6)
而式(6)中含有难以计算的高维积分,VB算法通过构造联合分布q(Cmis,Θ)来近似计算后验分布p(Cmis,Θ),运用Jensen不等式[15]得到:
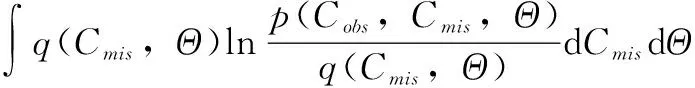
(7)
假定联合分布q(Cmis,Θ)是可分解的[16],得到对数边缘函数的下界函数:
F[q(Cmis)q(Θ)]=
(8)
将对数边缘函数与下界函数做差,可得:
KL(q|p)
(9)

与期望最大化算法类似,变分贝叶斯算法不断迭代地更新隐变量和模型参数的后验分布,直至算法收敛,得到真实后验分布p(Cmis,Θ|Cobs)的近似分布q(Cmis,Θ)[18]。
3.2 基于VB的辨识算法推导
3.2.1 模型参数的先验分布
p(θi|ηi) =N(0,ηi-1Dna ×na)

其中:D表示单位矩阵,g表示伽马分布,a0,b0,c0,d0为伽马分布的超参数,Γ表示伽马函数,其表达式为:

将上述先验分布用一个联合先验分布表示:
(10)
3.2.2 VB算法:E步
在E步骤中,固定参数集,关于隐变量对下界函数求极值,得到隐变量的更新后验分布q(I)。下界函数F[q(I),q(Θ)]可表示为:
(11)
求解如下优化问题:
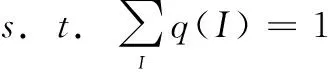
计算关于q(I)的拉格朗日函数的导数:
逐项求导后可以得到:
(12)
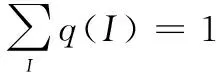
令:
得到:
(13)
其中:<·>q(Θ)代表对q(Θ)求期望。

(14)

由此可以将ZI表达为:
继而定义:
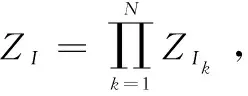
其中:q(Ik=i)可以表示为:
(15)
为简化表达,令:
I1:N|Θ,O)>q(Θ)}
式(15)可简化为:
(16)

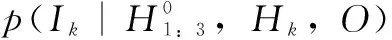
(17)
其中:
将Aki代入式(16)即可得到q(Ik=i)。
3.2.3 VB算法:M步
在M步骤中,固定隐变量,关于参数集对下界函数(11)求极值,得到参数集的更新式q(Θ)。下界函数可以表示为:
F[q(I),q(Θ)]=
(18)
其中:
下面利用拉格朗日乘子法,依次关于q(θi),q(ηi)和q(σi)最大化下界函数。
1)q(θi)部分:计算关于q(θi)的拉格朗日函数的一阶导数
可得:
-lnq(θi)+lnp(θi|<η1>q(η))+Cθ-
即:
q(θi)∝p(θi|<ηi>q(η))×
因此,q(θi)服从高斯分布,即:
其中:
(19)
2)q(ηi)部分:类似地关于q(ηi)对式(18)的求导:
可得:
-lnq(ηi)+(a0+1)lnp(ηi)-
其中:
整理后得到:
(20)
其中:Cη是与ηi无关的常数。由式(20)可知q(ηi)服从伽马分布,即q(ηi)=g(ai,bi),且:
3)q(σi)部分:关于q(σi)对式(18)的三部分求导:
可得:

(21)
其中:Cσ是与σi无关的常数。根据式(21)可知q(σi)服从伽马分布,即q(σi)=g(ci,di),且:
根据伽马分布的相关知识,可得:
(22)
(23)
最后通过非线性数值优化的方法求得局部模型宽度Oi的点估计,优化目标函数如下:
(24)
其中:q(Ik=i)由式(16)计算得到:
3.2.4 VB辨识算法计算步骤
基于VB的参数辨识算法计算步骤总结如下。
1)根据式(10)给模型的未知参数Θ设置合适的先验分布p(Θ),初始化未知参数Θ、O以及先验分布中的超参数a0,b0,c0,d0。
2)E步:关于隐变量最大化下界函数,根据式(17)计算Aki,并由式(16)得到隐变量Ik后验分布的更新式q(Ik)。
3)M步:固定隐变量,分别关于q(θi)、q(ηi)、q(σi)最大化下界函数,根据式(19)、式(22)以及式(23)得到各参数的期望E(θ)、E(η)以及E(σ),并根据式(24)计算局部模型有效宽度Oi的点估计。
4)根据以上两步得到的模型参数以及隐变量计算下界函数F:
5)将获得的估计值代入2),不断迭代计算2)~4),直至下界函数收敛。
4 仿真验证
本文利用来自文献[13]的10个100 000 L的青霉素流加发酵罐产生的数据训练并测试模型以验证模型对实际工业环境的适应性。实际工业过程中采集到的数据夹杂着大量噪声,以发酵罐排放气体中的CO2浓度(图4)为例。
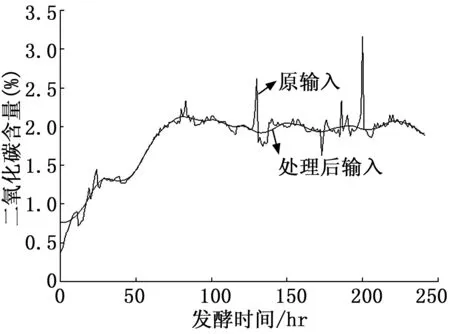
图4 预处理前后排放气体中CO2浓度图
为减少数据中的噪声对模型稳定性的影响,首先对输入数据中的异常值进行处理,由于发酵时间较长导致数据前后浮动较大,故本文首先根据发酵过程的阶段特性分阶段利用3σ准则剔除了输入数据中的异常值,然后对输入作滤波处理。
输入变量选择方面,在充分考虑反应机理并计算各输入变量与青霉素浓度相关系数后,选取5个过程变量作为输入变量,分别为:排放气体中CO2百分比(%),排放气体中O2百分比(%),pH值,C的生成率(g/min),发酵罐中物质总质量(kg)。利用本文第1节对葡萄糖流加速率进行聚类得到的典型工作点和经过预处理的输入数据,应用本文所述方法辨识得到子模型的参数,融合后得到青霉素浓度拟合曲线,如图5所示,其中三角形表示实际测量得到的数据。模型的质量通过相关误差进行测量,其计算公式如下:
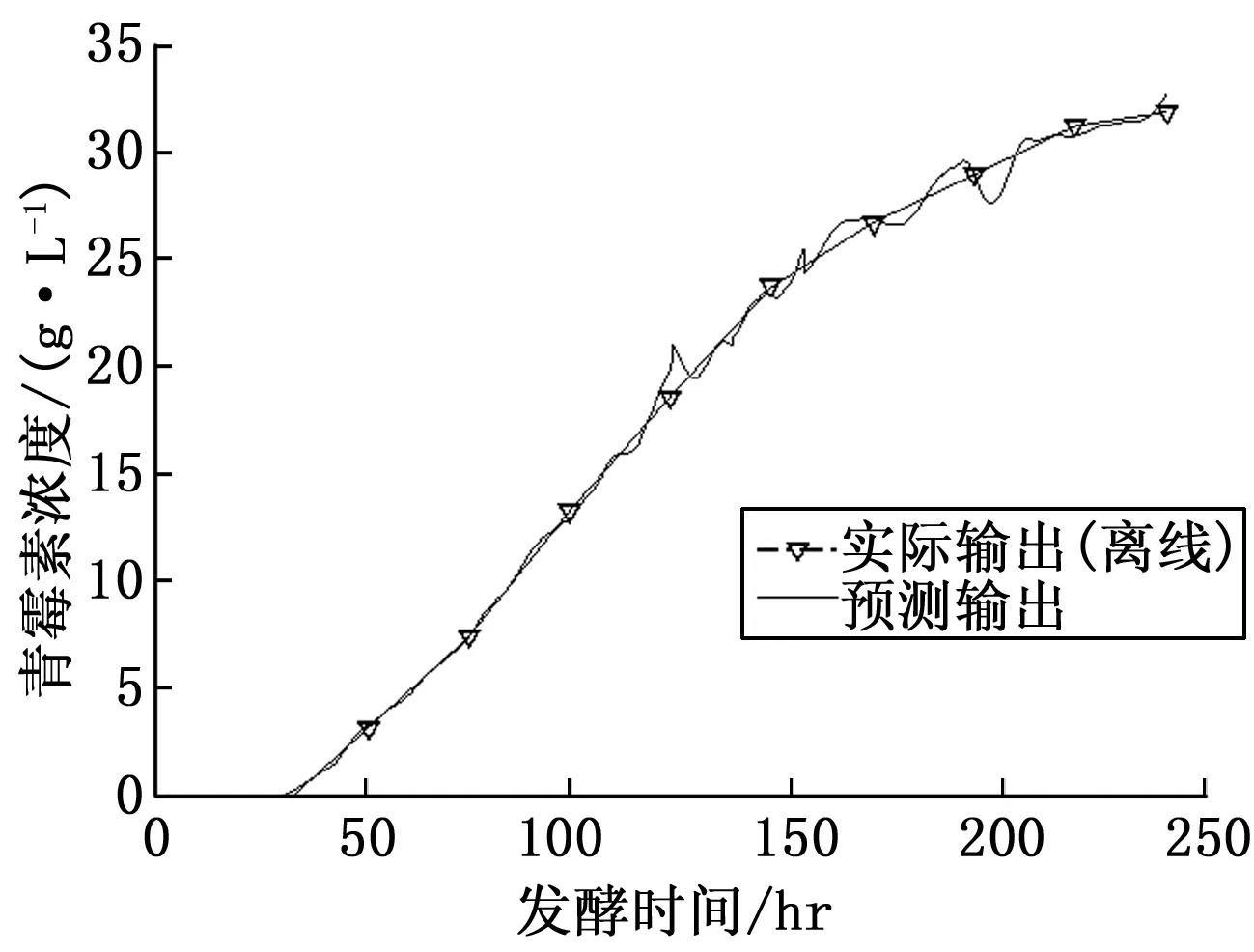
图5 青霉素浓度拟合曲线
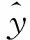
选取正常发酵情况下的另一批次数据对得到的模型进行测试,并与文献[9]中基于EM算法的青霉素发酵建模方法进行对比,预测结果如图6所示,计算得到本文模型与文献[9]的相关误差分别为0.23%和0.75%。

图6 对比实验结果图
可以看出,通过对青霉素发酵准确的阶段划分并充分考虑工业环境中的变化因素,本文所建立的模型能够更好地预测实际工业环境中青霉素发酵过程的产物浓度,对青霉素生产过程的控制与优化具有一定的指示作用。
5 结束语
本文采用变分贝叶斯算法建立了基于不同工作点的青霉素发酵过程各阶段子模型,采用由调度变量计算得到的标准化权值将子模型进行融合,变分贝叶斯算法通过估计参数的后验分布,能够将发酵中过程变量的不确定利用均值、方差等统计特性解析地表达出来,在环境复杂的工业青霉素发酵过程中表现出优异的性能。仿真实验表明本文方法能够精确建立青霉素发酵过程产物浓度模型,在复杂的工业环境中准确地预测青霉素发酵过程。
