现场条件约束下的动态诊断策略研究
2020-09-26廖小燕陆宁云
廖小燕,陆宁云
(南京航空航天大学 自动化学院,南京 211106)
0 引言
测试性是指产品能够及时准确地确定其状态(可工作、不可工作或性能下降),且对内部故障进行有效隔离的一种设计特性[1-2]。在测试性设计中,诊断策略优化设计是极其重要的内容之一[3]。诊断策略是结合目标、约束以及其他相关因素整体优化来准确对系统故障诊断的一种方法[4]。相比于传统的故障诊断方法,其侧重以故障诊断为目的的测试内容选取和调度问题,用以提升装备故障诊断的能力、提高诊断效率,进而提高装备使用度、降低装备整个寿命周期的费用[5-6]。
随着高新装备的发展,给装备的测试性设计和故障检测与诊断带来了很多问题[7-9]。故障诊断策略优化设计的主旨是以最小的测试代价生成最优的测试序列为目标的一种测试优化方法,其对于提高设备或系统的寿命、增强维修性能等都具有重要的意义[10-11]。传统的故障诊断策略设计方法属于静态的诊断方法,难以在复杂的装备系统中得到应用。主要问题表现于:维修人员只能按照固定测试步骤来开展故障诊断[12-13],而没有考虑在设备工作的现场条件约束,如缺少现场测试资源导致某些测试不能使用的情况;或者某测试因为其测试过程很简单导致其结果是直接可观测,用户主动选择该测试;亦或是某两个或者某几个测试之间存在相互约束的关系,即某个测试必须在另一个测试执行之后才能执行。本文主要考虑上述的现场复杂工况的条件约束下,提出了一种动态的故障诊断策略生成方法,该方法是以不可靠测试下的准深度优先搜索(Quasi-Depth First Search, QDFS)算法的故障诊断策略为基础,根据现场约束条件而确定下一步测试选择,最终生成完整的动态故障诊断策略。
1 问题描述
诊断策略是具有一定顺序的测试序列。当考虑到测试不确定性问题中出现的虚警、漏检的现象时,为系统故障诊断生成测试序列的问题包括以下部分:
1)有限的系统状态集合S={s1,s2,…,sm,sm+1},其中m为系统的状态总数,sm+1表示系统的无故障状态。
2)与系统状态集合S对应的状态先验概率集合P={p1,p2,…,pm,pm+1}。
3)有限的系统可用测试集合T={t1,t2,…,tn},其中n为可用测试的总数。
测试的代价集合C={c1,c2,…,cn}。
4)PT=[pdij,pfij]代表测试的不确定性,其中,pdij=P{O(tj)=1|fi=1},pfij=P{O(tj)=1|fi=0}分别表示测试的检测率和虚警率。
5)系统的故障与测试相关性矩阵D=[dij],其中dij=0表示系统状态si可以被测试tj检测到,反之,dij=1则表示系统状态si不能被测试tj检测到。
通过特定的算法,根据系统的相关性矩阵得到一组测试序列,以检测并隔离系统的各个故障状态,同时尽量减少预期的测试成本。估算测试费用的计算公式如下:
(1)
式中,Pi表示隔离系统状态si的测试序列,|Pi|表示这个序列中的测试数目。
2 现场约束条件分析
在实际维修过程中,现场可能出现某些测试不可用,用户需要主动执行某些测试,某些测试间存在顺序相关性等问题。本文充分考虑了这些现场约束条件,根据约束条件得到一个临时D矩阵,然后通过该矩阵,结合改进的准深度优先搜索算法计算得到当前被选测试,使得最终的诊断策略具有较高的实用性。
1)测试tj现场不可测的情况:
在现场工作环境中,也许会发生某些测试所对应的传感器短缺或故障等情况,从而导致需要的测试无法执行,使所需测试tj变得不可测。
2)用户主动选择测试tj的情况:
在现场工作环境中,维修人员也许会因为现场约束条件而主动选取测试tj,比如某些测试的结果直接表现出故障现象。
3)测试ti与tj存在顺序相关性:
在复杂的系统或者工况下,有些测试之间存在相互影响的情况,即存在某测试必须在另一测试执行之后方可用。
3 基于改进的QDFS算法的动态故障诊断策略生成
3.1 现场约束条件的描述方法
为了描述上述存在的各种现场约束条件,给出以下几个定义。
1)测试状态集St:
测试状态集St用来描述测试的可用或不可用的状态:
St={St1,St2,…,Stn}
(2)
其中:stj=0,1。当stj=0时表示测试tj的状态为测试不可用,stj=1时表示测试tj的状态为可用。
根据第2节中的约束条件一,可以知道当测试tj不可用时,St={1,1,…,0,…1,1};
2)测试-测试相关性矩阵:
为了描述测试与测试之间的顺序相关性,引出一种测试-测试相关性矩阵:
(3)
其中:ttij=0,1.当ttij=0时表示测试ti与tj之间不存在测试顺序相关性,当ttij=1时表示测试ti必须在测试tj之前执行,也就是说,如果需要执行测试tj,那么必须先检查测试ti的执行情况。
如果在某案例中,已经给定t1与t2存在顺序相关性,则tt12=1。那么当t1还未执行时,St2=0;当t1执行过后,St2=1。即
St2=(1-St1)·tt12
(4)
3)临时D矩阵:
每需要选取下一步测试时,都需要获得当前条件下的临时D矩阵。
对于约束条件一,某测试tj不可用,即stj=0,则临时D矩阵则是在上一步的D矩阵下删除不能用测试tj;
对于约束条件二,主动选择某测试tj,那么根据该测试的结果获得临时D矩阵,如果tj测试结果为通过,则选取原D矩阵中测试tj所在列对应的元素为0的所有的行为临时D矩阵的行,原D矩阵的列中删除tj的列为临时D矩阵的列。
对于约束条件三,测试ti与测试tj存在测试顺序相关性,则根据测试状态集确定下一步的待选的所有测试可用或不可用状态,然后取原D矩阵中对应的St中为1的测试和需要隔离的故障状态组成临时D矩阵。
3.2 改进的QDFS算法
准深度优先搜索算法是基于信息熵算法的单步向前回溯算法。该方法的基本思想是:使用信息熵算法分别构造一个以每个候选测试为顶点的临时诊断树,然后使用启发式函数k*计算并比较这些临时诊断树以获得最佳诊断树,而诊断树的第一个测试是当前的最佳测试。
1)初始化:
令系统的初始状态x为系统的所以状态集合S,初始测试集合t为系统所有的可用测试集合T。
2)信息量计算:
测试集合t中的每一个测试tj将状态集合x分为k个子集,计算每个子集的概率为:
(5)
更新每个故障子集的概率:
(6)
利用信息熵算法计算每个故障子集的最优故障诊断策略,并且以测试tj作为第一个测试生成临时故障诊断树Dj。
利用下面的启发式函数k*计算每个临时诊断树Dj的单位信息量:
(7)
式(7)中,IG(x;Dj)表示临时故障诊断树Dj的信息量,COST(x;Dj)表示临时故障诊断树的平均测试代价,Pr(tj)表示测试tj的故障检测能力,R(tj)表示测试tj的可靠度。
(8)
(9)
(10)
(11)
3)测试选择:
从集合t选择单位测试代价具有信息量最大的测试:tq。
4)概率更新:
系统状态集合x被测试tq划分为2个集合,分别为xq0,xq1,更新每个子集的的故障概率。
5)重复:
令测试集合t为除去测试tq的原测试集合,令状态集合x为原状态集合的各个故障子集。重复第2)~4)步,直到各故障状态子集中的元素少于或等于1,或者测试集合t中元素少于1。
3.3 诊断策略生成过程
在诊断策略设计过程中,首先利用TEAMS软件工具建立系统的多信号模型[14-16],得到被诊断对象的D矩阵,然后在实际诊断过程中随外部控制条件,如症状、资源等变化获取所有的测试状态集合St,并根据原D矩阵获取下一步的临时D矩阵,在临时D矩阵基础上利用改进的准深度搜索算法产生下一步最佳的测试,再根据测试执行情况调整测试状态集合St,生成新的临时D矩阵,然后利用改进的准深度搜索算法,直至得出最后的诊断结论。具体步骤如下:
1)根据系统的结构原理,得到系统故障测试相关性矩阵D,故障状态集S,各个状态对应的故障先验率P,可用测试集T,测试对于费用集合C,各个测试对应的检测率和虚警率等。
2)初始化。令系统初始故障状态集合x=S,初始测试集合为t=T,初始测试状态集合St={0,0,…,0},从现场工作条件中获得现场存在的初始条件约束。
3)根据当前的条件约束更改测试状态集合St。如果有某测试不可用,则令该测试对应的stj=0;如果前面执行算法的过程中有某测试不可用但当前条件使某测试可用了,则令该测试的状态stj由0变为1;如果某些测试存在顺序相关性,则后面的测试对应的状态stk=(1-stl)ttlk。
4)根据当前测试状态集合确定可用测试集t。取测试状态集合St中的为1的元素对应的测试为可用测试集合t。
5)根据当前的故障状态集合x,测试集合为t,生成临时D矩阵,用上一节的启发式搜索函数(式(6))选择下一步测试tq。
6)系统状态集x被测试tq分为两个子集,更新系统故障率。
7)令系统状态集x为6)中的子集,将已执行的测试对应的状态更改为0,并从现场工况重新获得当前的条件约束,重复3)~6)直到St中元素全为0或者所有x中元素数不超过1。
由此形成的诊断策略就是动态诊断策略生成过程,如图1所示。

图1 动态诊断策略生成过程
4 案例分析
为了验证在现场约束条件下所提出的方法能生成有效的测试序列问题,使用经典的Apollo检测系统[17-19]进行案例研究。阿波罗探测系统是一个复杂的系统,其物理结构和测试条件比较复杂。已知Apollo检测系统的故障测试相关性矩阵D和故障概率的分布如表1所示。每种测试的检测概率,虚警概率和成本如表2所示。

表1 Apollo系统的故障测试相关性矩阵

表2 Apollo系统的测试参数
在没有现场约束条件的情况下,根据改进的QDFS算法生成的不可靠测试条件下的静态故障诊断策略如图2所示,该诊断策略的总代价为132.85。
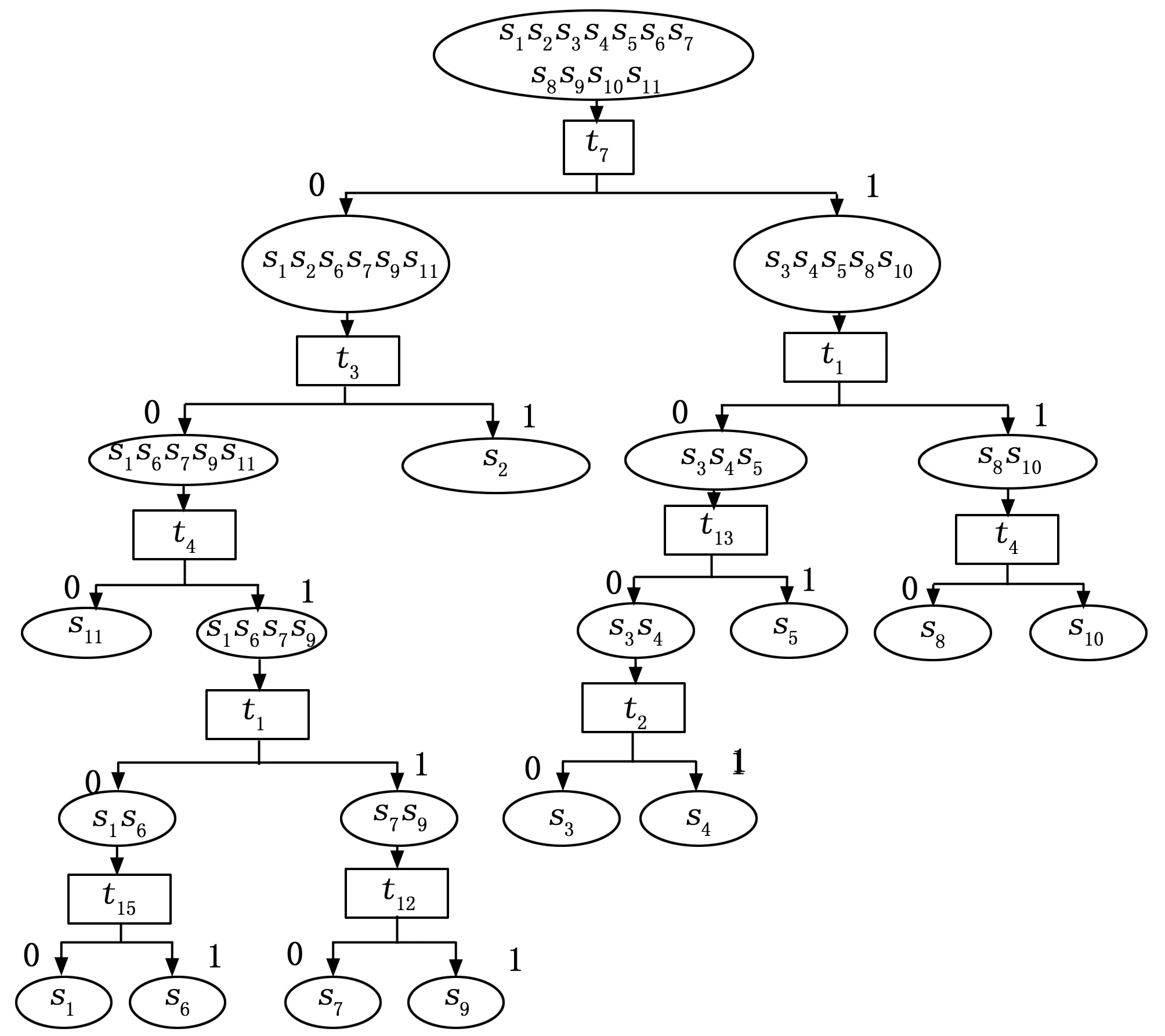
图2 Apollo系统的静态诊断策略
接下来考虑在现场约束条件下的诊断策略。
假设在某一次检测中发现测t4出现故障现象,即t4测试结果直接可观测,并且t12对应的传感器出现故障,即t12不可测,并且存在现场测试的顺序相关性约束,t15必须在t1的后面执行。
根据条件约束一和二,可以得到表3所示的临时D矩阵。如果不考虑t15和t1的顺序相关性,可以获得的诊断树如图3所示,从图中可以看出,因为现场约束条件的影响,测试可用的选择数变少,需要隔离的故障数目更是大幅减少,所以故障诊断树变得很简单,且只需要三步就能隔离出全部故障。由于测试t4的结果直接观测得到,为此省略了一些故障隔离的步骤,所以得到的该故障诊断策略的代价也比正常的静态的故障诊断树的代价要低,为117.82。
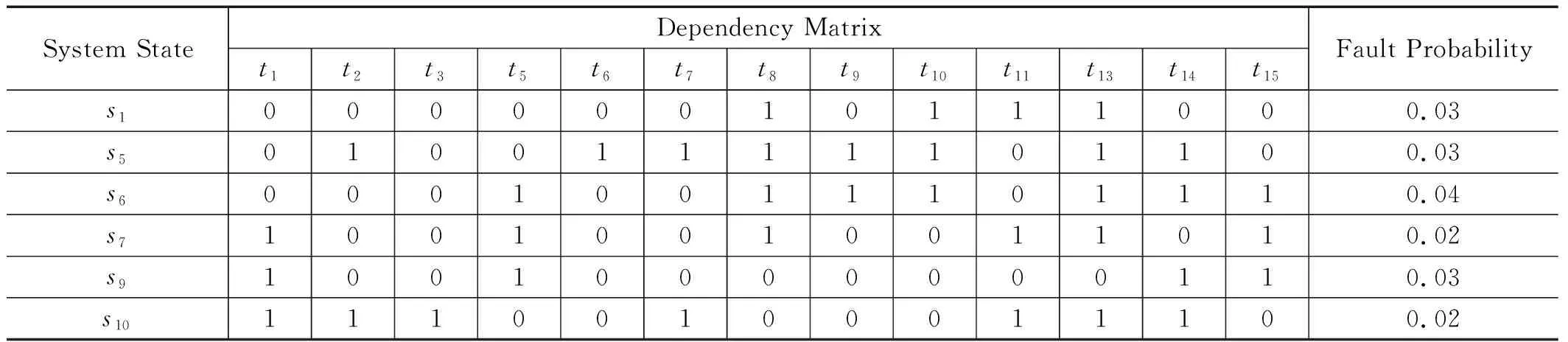
表3 Apollo系统的临时D矩阵

图3 案例四的动态诊断树(1)
上述分析并没有考虑约束条件三的影响,从上面结果可以看出,测试t1和测试t15都有被选择,但是t1和t15约束条件三相违背。所以在进行第二步隔离时,希望选择t1作为该步骤的测试,但是t15还没执行,所以t1也不能执行。所以此时的临时D矩阵是没有t1作为备用测试的。根据第三章的所提的改进的诊断策略生成算法,这一步对于隔离s1,s6,s7,s9所选的测试为t1,而隔离s5和s10所选的测试为t6.对于s1,s6,s7,s9执行完t15之后,被分为s1和s6,s7,s9两个子集,接下来对s6,s7,s9进行诊断策略生成,而这时候因为t15已结执行完毕,测试t1变为可用测试,接下来直接将改进的准深度搜索算法应用到此时的临时D矩阵即可生成最终的故障诊断策略,如图4所示。
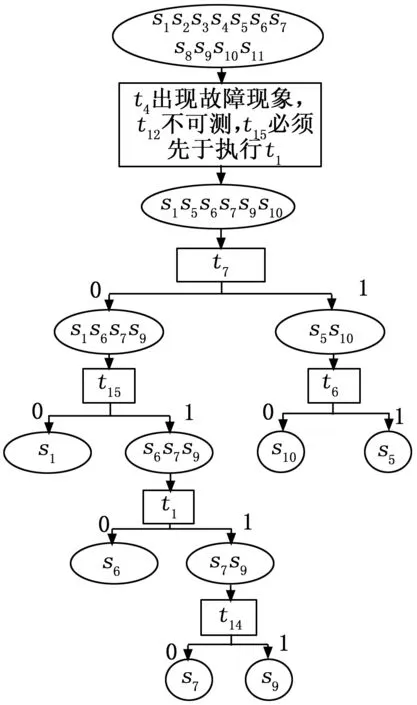
图4 案例四的动态诊断树(2)
由图4所示的结果可以看出,诊断策略由于约束条件的影响,变得稍微复杂了一些,但正是由于约束条件的影响,得到的诊断策略更符合现场工况,所以当前方法更适用于现场条件约束下的动态故障诊断策略生成。
5 结束语
复杂的系统或现场工作环境使得设备具有许多测试点和复杂的故障模式,除了虚警和漏检等测试的不确定性问题,现场条件约束更是故障诊断策略生成方法中不能忽略的问题。目的是在现场复杂工况的约束条件下,设计一种不可靠测试下的诊断策略生成方法,重点考虑了测试不可用,主动选择某测试和测试之间存在顺序相关性的问题。结果在Apollo案例中进行了验证,结果表明,在允许的时间范围内,当前算法都更加符合设备现场工作环境,增加了故障诊断策略的有效性和实用性。这对于复杂系统和现场条件约束下的故障诊断策略设计具有重要意义。
