超声对近壁微气泡溃灭过程的影响*
2020-09-25王舰航陈韬厚包福兵王月兵
王舰航 陈韬厚 包福兵 王月兵
(中国计量大学计量测试工程学院 杭州 310018)
0 引言
近些年来,基因治疗技术获得了飞速发展,被认为是最有前景的癌症治疗方法之一[1]。超声靶向微泡破坏技术作为一种新型的基因转染方法,相比较于病毒和物理等其他转染方式,应用潜力大[2],利用超声作用诱发细胞膜声孔效应来实现基因转染,高效且安全。Taniyama 等[3-4]通过电镜观测到超声作用下细胞膜上产生可恢复的孔洞,验证了超声靶向微泡破坏技术的可行性和超声微气泡转染基因的安全性。微气泡在超声作用下还可用于高效的药物靶向输运,Zhang等[5]和Li等[6]深入研究了微气泡的超声空化效应,携带药物的微气泡在超声作用下空化溃灭时能够实现药物的靶向释放,从而达到精准医疗的目的。
超声作用下近壁气泡会出现非对称溃灭,气泡溃灭的复杂性使得现有基于Rayleigh–Plesset 方程的球泡理论不再适用,更多学者选择使用数值模拟或实验方法进行研究。刘兰等[7]和Lechner等[8]基于不同平台研究了近壁微气泡在水中的空化过程,对比了蒸汽泡和空气泡在溃灭形态和射流速度、溃灭压强的异同。Wang等[9]和Ma等[10]研究了近刚性壁面的溃灭与界面的相互作用。张宇宁等[11]和张亚磊等[12]通过实验分析了水中近壁气泡的溃灭过程。Alhelfi 等[13]、Kerboua 等[14]和Wang 等[15]分析研究了超声波波形对溃灭气泡内部压力、表面速度等性质的影响。Shen 等[16]基于COMSOL 平台模拟了超声场下血管壁附近气泡溃灭过程。Curtiss 等[17]和Wang 等[18]研究了超声微气泡空化对组织层和细胞变形的作用。Brennen[19]对超声在医学上的应用做了综述。目前的研究更多集中在超声作用下微气泡的一次溃灭上,对气泡的二次溃灭的分析较少。本文主要通过数值模拟方法,研究近壁微气泡的空化溃灭全过程。
1 数值计算方法
1.1 理论模型
为分析近壁微气泡在超声作用下的溃灭过程,采用有限体积法结合流体体积模型(Volume of fluid,VOF)[20]来模拟气液两相运动。VOF 模型是用相体积分数表示流体自由面的位置和流体所占的体积,假设在计算中每一个控制体第一相的体积含量为α1,如果α1=1,表示该控制体积内只有第一相,如果α1=0 则表示不含有该相,如果0<α1<1,则表示该控制容积中有两相交界面存在。因此VOF 多用来处理没有相互穿插的多相流问题,但是VOF模型要求所有控制体积必须至少被其中一种流体相混合或者充满,既不能出现无流体的区域,再者,VOF模型只允许有一相可压缩流体,本文假设气相为可压缩相,液相为不可压缩相,所以该模型在本文中是适用的,连续性方程和动量方程分别为

其中,u为流体的速度矢量,ρ为流体密度,μ为流体黏度。
采用VOF模型来跟踪气液两相界面,体积分数方程为

其中,αl为液相的体积分数,值为0 表示气相,值为1 表示液相,取值在0<α<1 表示气液界面。方程中流体密度和黏度表示为

其中,下标l和g分别代表液相和气相,并且有αl+αg=1。
1.2 计算方法

图1 计算示意图Fig.1 Computational schematic diagram
本文选取二维轴对称计算域进行计算,如图1所示,计算域为500 μm×250 μm 的矩形区域。边界AB为壁面,壁面是无滑移静止刚性壁面边界条件,边界AD为对称轴,边界BC和CD为压力边界条件。二维轴对称气泡放置在壁面附近,气泡中心与壁面的距离为L,定义一个无量纲参数γ来表示近壁距离:

1.3 边界条件
在计算中,流体域初始速度为0。在BC和CD边界施加超声作用,直接给定压力变化:

式(7)中,pl为液体静压,初始值设为一个标准大气压,pd为声压振幅,f为超声频率,t为时间。
气泡内初始压力遵循以下公式[21]:

式(8)中,pg为初始气泡内部压力,σ为表面张力系数,本文中取σ=0.0735 N/m。
由Rayleigh 理论中公式[22]可知气泡溃灭时间为
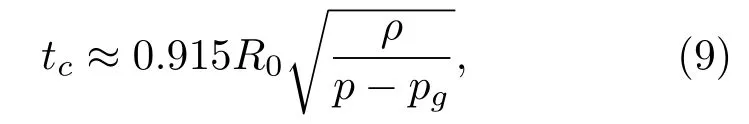
式(9)中,R0为气泡最大半径,pg是气泡内部压强。
为了更好地描述气泡在超声作用下的溃灭过程,引入无量纲时间:

其中,T为驱动声压的周期。
1.4 网格无关性验证
本文采用结构化网格对计算区域进行了网格划分,为提高计算精度,在气泡附近区域进行网格加密,采用可更好地同时满足动量方程和连续性方程的PISO 算法来求解Navier-Stokes 方程,连续性方程和动量方程的残差小于10-6,能量方程的残差小于10-7。在一个超声周期内计算1000步,每一步迭代50次,时间步长Δt=10-3T。
以R0=100 μm、f=30 kHz、pd=300 kPa为例对网格无关性进行验证。选取5 套网格对气泡的溃灭过程进行数值模拟,网格数分别为16905、44104、104544、228536 和330872。参考文献[23]中Rayleigh-Plesset(R-P)方程近似解析解计算方法,同时将计算结果与Rayleigh-Plesset(R-P)方程的近似解析解进行对比。不同网格气泡体积变化如图2所示,其中V0为气泡的初始体积。

图2 不同网格数下气泡体积随时间变化Fig.2 Variation of bubble volume with time under different mesh numbers
从图2可知,在气泡溃灭前,网格数量的影响不大。气泡达到最小体积后回弹时网格数量对气泡体积的影响较大,且气泡体积随网格数量增加而变大,但体积增量逐渐变小,当网格数为228536和330872时,气泡回弹体积基本一致,此时认为计算结果与网格无关,计算精度足够,因此取网格数228536 来进行后续模拟分析。与控制无限不可压缩流体中单个球形气泡动力学的R-P 方程近似解析解相比,理论结果和本文模拟结果高度拟合,验证了本文模型的准确性。
2 结果与讨论
2.1 超声作用下的微气泡近壁溃灭过程
由于超声的作用,微气泡内外的压差使微气泡体积发生变化,在超声作用下气泡会出现形状振荡[24]或者溃灭等现象,气泡是否溃灭与超声的频率和强度等参数有关。当气泡附近存在壁面时,气泡出现不均匀收缩,气泡近壁面端收缩较慢,图3 中左侧为速度流线图,右侧为压力云图,黑色实线为气泡轮廓。如图3(a)所示气泡在t=3.450 μs 时,气泡开始由远壁面端向气泡内部收缩;如图3(b)所示t=3.620 μs 时,气泡远离壁面端外部压力达到最大,气泡凹陷开始出现射流,此时达到气泡溃灭阶段最大射流速度,超过250 m/s。外部液体受压力驱动继续流向气泡,气泡受外部流体的夹带,在凸起侧部形成漩涡;随时间推移,外部液体沿壁面向远离气泡方向流动,如图3(c)所示气泡在t=3.725 μs时,漩涡上移至凸起顶部,气泡内高速流体起主导作用带动气泡向壁面移动。气泡体积的减小导致其内部压力升高,在惯性的同时作用下射流向壁面移动,气泡被压缩到最小;在t=3.845 μs时,如图3(d)所示射流穿透气泡,溃灭瞬间压强在穿透点处达到最大,中心射流将气泡分成两个稍小的气泡。

图3 超声近壁微气泡溃灭过程,R0=100 μm,f=30 kHz,pd=300 kPa,γ=1.3Fig.3 Ultrasound near-wall microbubble collapse process, R0=100 μm, f=30 kHz, pd=300 kPa, γ=1.3
一次溃灭产生的中心射流将气泡分成两个稍小的气泡,且在中轴线处存在碎小气泡向远离壁面方向移动;一次溃灭结束后气泡开始二次溃灭,如图3(e)所示,高速射流受到壁面阻碍,液体沿壁面流向两侧,与其他部分流向气泡的液体在气泡边界相遇产生旋涡。此时气泡内部的势能通过射流的形式转化为动能,泡内压力骤降,且分裂后的气泡受外加超声影响被二次压缩;分裂后的气泡生长如图3(f)所示,流体远离气泡流动,中轴线的碎小气泡继续上移。在射流冲击之前,液体流动是沿中轴线向壁面流动,但射流撞击壁面后,射流通道内的液体流动速度显示出不同的方向,向下流动停滞后转而向上流动,产生了反射流;如图3(g)所示,微气泡界面存在压差使得分裂后的两个气泡体积被继续压缩,周围的液体向气泡运动,反射流与壁面附近流向气泡的流体在中轴线相遇形成漩涡,此时气泡已经完全分裂为许多更小尺度的碎气泡;溃灭的末期如图3(h)所示,原先的单个大气泡分裂为多个碎小气泡的泡群继续膨胀压缩,由于壁面存在而产生的射流通道对溃灭过程的影响,溃灭末期的流场复杂,中轴线以及壁面附近形成多个漩涡,碎小气泡分散在中轴线附近,该尺度下的溃灭结束。
气泡溃灭过程中其形态和流场中各物理量会发生剧烈变化。如图4所示,气泡在整个溃灭过程中的泡内压力、最大射流速度以及气相体积变化过程。在第一次溃灭时,气泡最大压力、最大温度最大射流速度以及最小体积基本同时发生,压力最大能达到10 MPa,速度最大达到250 m/s 左右,最大温度850 K 左右。一次溃灭结束后,气泡开始反弹膨胀,此时气泡内部压力及速度均开始减小,当分裂后的气泡膨胀到最大体积时,气泡收缩,二次溃灭开始,此时研究对象为两个被分裂的小气泡,其收缩区域的最大压力和温度明显小于一次溃灭,但最大射流速度却达到350 m/s,远大于一次溃灭的速度,这意味着溃灭作为一个完整过程,二次溃灭的影响甚至要大于一次溃灭。

图4 二次溃灭过程各参数随时间变化,R0=100 μm,f=30 kHz,pd=300 kPa,γ=1.3Fig.4 Each parameter of the secondary failure process changes with time, R0=100 μm, f=30 kHz,pd=300 kPa, γ=1.3
2.2 最大射流速度
近壁微气泡溃灭时的最大射流速度是一个关键指标,对壁面有重要影响,其中无量纲近壁距离是影响最大射流速度的一个关键参数。图5 给出了初始半径分别为60 μm、80 μm 和100 μm 的3 种微气泡在频率为30 kHz的超声作用下,在不同近壁距离时溃灭产生的最大射流速度的变化。
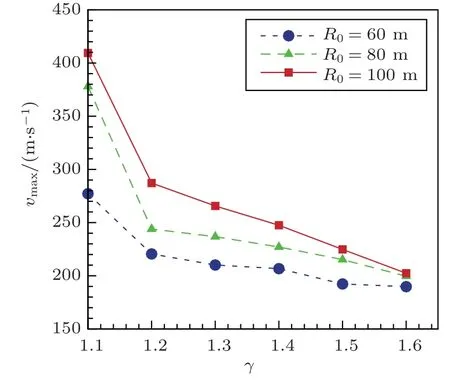
图5 最大射流速度随不同壁面距离的变化Fig.5 Variation of maximum jet velocity with different wall distances
从图5 中可以看出,随着近壁距离γ的增加,气泡离壁面距离增大,壁面对气泡远壁面端的影响不断减弱,气泡溃灭的最大射流速度逐渐降低,与文献[25]中的速度变化趋势相同。气泡距离壁面越近,其运动受壁面限制越明显;当气泡远离壁面时,壁面对气泡的影响逐渐减小,其所受周围流体的压缩趋于均匀,射流已经不能完全穿透气泡,气泡溃灭时产生的射向壁面的速度也越小。
超声波频率对气泡溃灭最大射流速度也有重要影响。图6 给出了初始半径分别为60 μm、80 μm和100 μm的3 种微气泡,距壁面的无量纲距离恒为γ=1.3 时,不同频率的超声波对最大溃灭射流速度的影响。从图6 中可以看出,气泡溃灭时的最大射流速度随超声频率的增加而降低,与文献[26–27]所研究的速度变化趋势相同,对比文献[28]在相近频率范围内的模拟结果,超声频率的增加意味着溃灭周期缩短,气泡没有足够的时间去储存和释放能量,溃灭就已经开始,表征在最大射流速度上便是频率增加导致能量吸收不足,最大射流速度变小。
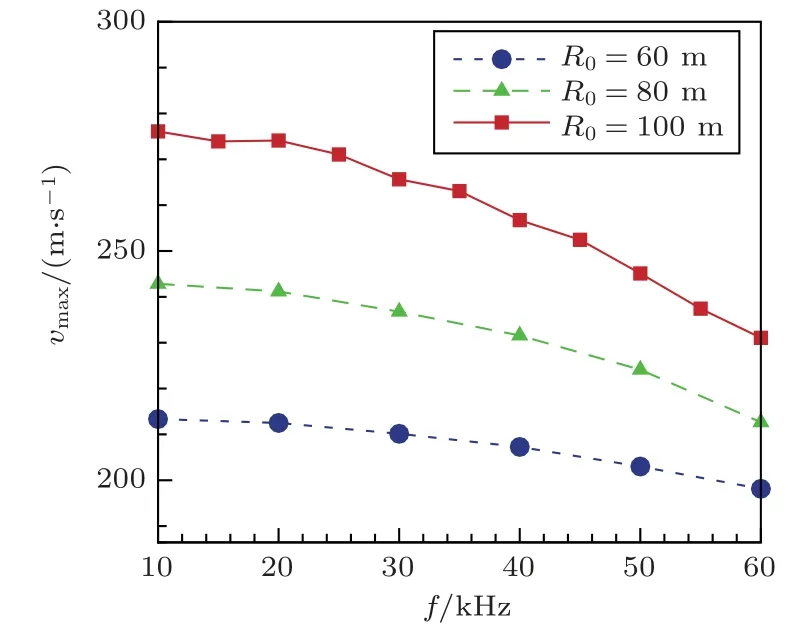
图6 最大射流速度随不同超声频率的变化Fig.6 Changes of the maximum velocity with different ultrasonic frequencies
气泡初始半径也会对最大溃灭速度产生影响。图7 给出了频率分别30 kHz、40 kHz、50 kHz 的超声作用下,距壁面的无量纲距离恒为1.3 时,不同初始半径的微气泡溃灭时的最大射流速度的变化。从图7 中可以看出,气泡溃灭最大射流速度随气泡半径的增加而增加,这与Oguchi 等[25]的研究结果中最大射流速度随超声频率的变化趋势相同。从能量角度分析,气泡系统的内能、动能与势能之和等于气泡的原始势能与施加超声波的能量,同等超声波能量下,初始半径越大,原始势能越大,因此产生的最大射流速度相应增加。

图7 最大射流速度随不同初始半径微气泡的变化Fig.7 Changes of maximum velocity with microbubbles of different initial radii
3 结论
本文采用数值模拟方法研究了超声对近壁微气泡溃灭过程的影响。给出了超声作用下近壁微气泡溃灭过程中的气泡形态和流场变化,针对本文所用超声参数产生气泡射流穿透气泡的情况,分析了微气泡近壁距离、初始半径和超声频率对最大射流速度的影响,结果表明气泡溃灭最大射流速度与近壁距离无量纲参数γ在1.1~1.6 范围内时成正比,与超声频率在10~60 Hz 范围内时成正比,与气泡初始半径在50~100 μm 范围内时成反比;同时给出了二次溃灭过程中微气泡附近流体运动情况,并发现二次溃灭所能达到的最大射流速度要大于气泡一次溃灭,相关结论对超声靶向给药和基因治疗等技术提供理论依据。
