财政补贴对企业创新的影响效应及其异质性检验——基于我国上市公司的经验分析

郭娟娟，熊如意，肖建华，秦 甄

（1.南昌理工学院 国际交流学院，江西 南昌330044；2.江西财经大学 财税与公共管理学院，江西 南昌330013）

一、引言与文献综述

财政补贴一直是理论界与实践界共同关注的重要话题，就其与企业技术创新关系来说，理论工作者对其进行了大量的探讨且形成了诸多有益成果。总体来看，其主要观点大致可以分为三类：第一，财政补贴具有“激励”效应。其主要观点认为财政补贴对企业研发具有促进效应［1-3］，这是因为财政补贴降低了企业自身R&D 投入成本和风险，缓解企业创新活动中资金不足问题，帮助企业（尤其是中小企业）跨越创新初期的“死亡之谷”［4］，可以帮助解决企业创新活动所带来的私人收益小于社会收益等问题。第二，财政补贴具有“扭曲”效应。其主要观点认为由于信息不对称，财政补贴资金的分配过程中会出现寻租和腐败，会扭曲社会资源的有效配置，从而降低补贴效果［5-6］。此外，周燕等还发现，在一些高科技行业（如生物医药产业）还存在企业通过数据造假“过票”方式来增加营业额，从而达到获取财政补助的现象［7］。第三，财政补贴具有“混合效应”。其主要观点认为财政补贴效果不能一概而论，如Lach Saul对以色列制造业企业1990-1995年的数据进行实证分析，发现财政补贴对小企业的研发投入具有很强的促进作用，而对大企业却表现出明显的负相关关系［8］。武咸云认为财政补贴与企业创新投入间呈倒“U”形关系，即政府R&D补贴有一个最优补贴值，在最优值以前，会激励企业的创新投入，但是超过该临界值后，就会部分或完全挤出企业自身的研发投入［9］。Gonzalez等以西班牙制造业为例，发现补贴虽然只能小幅度地增加企业研发投入，但若没有补贴，企业会大幅缩减研发投入甚至不投入［10］。此外，Gonzalez 和Pazo 认为，财政补贴对研发投入的激励效果取决于研发回报率，当研发回报率较低时，企业只有在获得补贴的情况下才会增加研发投入，那么补贴是有效率的；反之，补贴会挤出企业私人研发投入，导致补贴无效率［11］。

我国一直重视运用财政补贴来激励企业进行创新投入。近年来财政补贴规模持续走高，覆盖面也呈扩大之势。根据上市公司财务报告披露的信息来看，2010 年所有上市公司获得的财政补贴金额约为381亿元，每家获得财政补贴的公司平均补贴金额约为0.21亿元，而到了2017年，所有上市公司获得的财政补贴金额达到1 302 亿元，增长了3倍多，每家公司平均获得的补贴金额也增加至0.39亿元。与此同时，财政补贴的覆盖范围也日益扩大，2010 年上市公司中获得财政补贴的公司占比约为89%，而2017 年这一比例已升至97%，几乎覆盖所有上市公司［12］。那么，这些上市公司为何能获得财政补贴，财政补贴对其创新投入究竟发生了什么作用，在各行业、各地区的影响具有什么样的差异？以此为研究起点，本文尝试从经济学理论层面构建理论模型对财政补贴政策的实质进行探讨，并在此基础上以我国上市公司公开数据为样本，实证分析财政补贴对企业创新的具体支持作用。本文下面的结构安排如下：第二部分是理论模型与研究假设，尝试用经济学理论模型论证财政补贴与企业研发的定性关系；第三部分，设计计量模型选择、数据和变量说明；第四部分基本回归结果报告，异质性分析和稳健性检验；第五部分是研究结论与主要政策建议。

二、理论模型与假设

基于新增长理论构建经济学模型，一般假定经济体中存在两个部门，分别为生产部门和研发部门，企业的资本在两部门中进行分配，资本中有r的比例投入到研发部门，（1-r）的比例用于生产部门，现有技术水平为A。假设适用柯布—道格拉斯生产函数，为了简化分析，不考虑劳动力条件，其表达式为：

其中，1＞α＞0，代表企业生产资本的系数。当考虑企业获得财政补贴的情况下，假设财政补贴率为s，则企业用于研发的资本投入可以表示为（1+s）r，而用于生产投入的资本为（1+s）（1-r），则生产函数可以表示为：

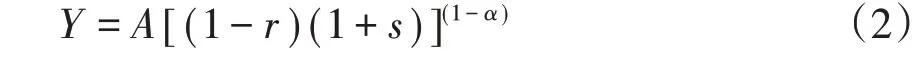
假定新技术的产生取决于进行研发的资金投入和现有技术水平，其表达式为：

其中，θ 刻画了现有技术水平对研发成功率的影响［13］，B为转换参数。假设企业的资本研发投入存在边际报酬递减的情况，设定研发投入资本带来技术进步程度提升的边际效果是下降的，因此假设∂＝0.5。同时假设θ＝1，即现有技术水平与技术进步成正比，并考虑财政补贴率s，则技术进步程度为：

当经济体考虑长期产出，如考虑连续两个时期（比如两年）的经济总产量，可以得出连续两个时期的总产出Y，结合式（2）和（3）式，得到下式：

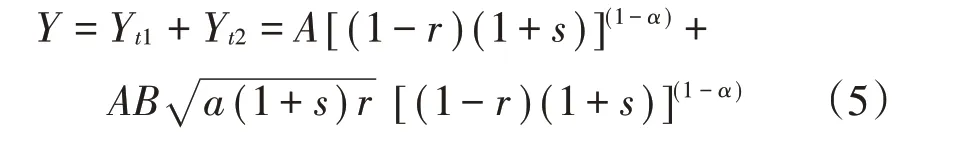
公式（5）表明，企业进行研发活动决策时不仅会基于当期产量，而且会影响未来预计产量；为了实现长期总产出最大，基于原有技术水平，可以选择通过研发实现技术进步，进而提高产量。据此可以推出：实现连续时期总产出量最大时的研发投入比例r与财政补贴率s之间的关系式如下：

根据（6）式，不难发现，在不考虑其他因素变化的情况下，当财政补贴率s 增大时，企业的研发投入比例r会增加，即财政补贴率s越高，企业越有动机进行研发活动。

三、模型、数据说明与变量选择

从理论分析来看，实证分析的主要任务是探究企业研发投入与财政补贴率间的关系，分析其区域及行业异质性，并进而分析企业获得财政补贴的原因。

（一）计量模型

为了实证分析财政补贴对企业创新的实际效果，检验理论模型，首先构建如下计量模型。

被解释变量lnrdi,t表示企业研发投入金额的自然对数。

核心解释变量lnsubsidyi,t表示企业获得的财政补贴金额的自然对数。这里需要说明的是，在实证分析中曾尝试采用多种形式的补贴变量对模型进行拟合，包括采取文献中常用的滞后期的财政补贴数值，然而经过多次试验，最终证明只有当期的财政补贴才能得出显著性结果，后文也证明了该结果的稳健性。为了增加模型的说服力，后文也将探索当期补贴而不是滞后一期补贴对研发投入会产生显著性影响的政策性原因。

向量集Ai,t表示影响上市公司进行创新活动的其他控制变量；i表示企业，t表示年份；μi,t表示各个上市公司的个体效应；εi,t为随机扰动项。

考虑（7）式并未控制研发投入的滞后期，而这种变量遗漏可能导致严重内生性问题。为此，构建基于动态面板数据的两阶段差分广义矩估计（Difference-GMM）和系统广义矩估计（System-GMM）模型。

在（8）式的右边，引入了被解释变量的滞后一期（lnrdi,t-1），但在确定前也尝试引入核心解释变量的滞后期和被解释变量的滞后二期，结果并不显著，因而此处未列入方程。模型主要关注系数β1，在控制了内生性问题之后，如果财政补贴对企业创新具有正向激励作用，则β1仍应显著为正。此外，被解释变量的滞后一期系数α1也值得关注，若其是显著的，则说明被解释变量确实存在自相关性，建立动态面板数据模型是有必要的。

（二）数据说明

选取2014-2018年国内上市公司作为样本，并对样本进行以下筛选：①剔除ST公司以及当年IPO公司。②剔除含B股的上市公司，这些公司面临境内外双重监管环境，与其他上市公司不同，为了集中于本文所要研究的问题以及计算公司价值的方便，本研究剔除这些公司。③剔除被划分在两个及两个以上板块的重复企业、数据披露不完整的企业以及实际研发补贴额小于零的企业。此研究的样本属于短面板，因此可以忽略时间效应。此外，为了审查数据质量，随机抽样比较两个数据库中的数据，并使用上交所和深交所披露的企业年报解决差异。为减小偶然因素的影响，对样本数据进行1%的winsor 处理，最终得到10 711 个样本，财政补贴与研发投入数据主要来源于上市公司年报手工收集，其他数据来源于国泰安数据库（CSMAR）和Wind数据库，使用stata 15.0软件进行处理。

（三）变量选择

根据设定的实证模型，对所选择的变量具体说明如下：

（1）被解释变量。选取A股上市公司研发资金投入的自然对数（lnrd）为被解释变量。一般认为，R&D投入主要包括研发资金投入和人力资源投入两方面内容，但考虑两者之间具有很强的共线性，因此测度补贴效果时只需考虑其中一方面。另外，本文之所以采用绝对数值而非相对数值来衡量企业创新，是因为考虑政府财政补贴企业创新的初衷是推动企业增加研发投入绝对值，而非要求企业提高相对值。

（2）核心解释变量。主要采用财政补贴金额的自然对数（lnsubsidy）。财政补贴采用了企业当年所获补贴总额的自然对数，并未细分为创新类补贴，主要有以下原因：第一，从企业公布的补贴项目明细中了解到，创新类补贴占据补贴总额的绝对比例，采用补贴总额作为替代也能具有较强的解释力；第二，各个企业公布的补贴明细中，补贴项目纷繁复杂、名目繁多，而且企业获得的补贴未必会专款专用，因而无法轻易分离出专用于研发的财政补贴。此外，同被解释变量一样，核心解释变量也是采用企业获得财政补贴的绝对值而非相对值，是因为考虑现有补贴政策对企业进行补贴时并不是以相对值来补贴，而是根据企业创新的产品进行绝对值补贴，例如新能源汽车补贴是按照汽车里程或能源消耗进行补贴。

（3）其他变量。在前人成果的基础上，以净资产收益率（roe）、股权集中度（z）、企业偿债能力（ldrate）、企业创新能力（yy）、公司总资产（assets）、总资产周转率（ttm）、企业年龄（age）和股本（capital）为控制变量，并设置是否国有控股（SO）、产业类别（industry）和地区（local）为虚拟变量。企业偿债能力用企业流动比率来衡量；企业创新能力用企业拥有的专利数量来测度［14］，而考虑有些专利“掺水”情况［4］和数据的可获得性，将企业当年的营业收入作为企业创新绩效的综合反映指标［15］。

为控制异方差问题，所有连续变量都取对数。各变量定义与计算口径见表1所列。

表1 变量定义与计算口径

（四）描述性统计结果分析

表2 报告的是主要变量的描述性统计结果。根据表2，对研发和补贴金额进行取对数处理后，中位数和均值大概相等，说明数值分布较均匀，且方差的数值不大，说明数据的波动性较小，有利于后续的实证检验；从对净资产收益率（roe）的描述中不难发现，有相当多的样本公司净资产收益率为负值；股权集中度（z）和流动比率（ldrate）的均值和中位数的差距较大，而且中位数靠近最小值，即样本值明显左偏，这说明样本中大多数企业的股权集中度较低，即股权较分散；流动比率是用来衡量企业的短期偿债能力，流动比率中位数为1.8，说明样本中流动比率数值有一半低于2，即有一半样本企业的短期偿债能力偏低。其他的变量描述性统计结果均符合统计学要求。

图1 显示的是两个核心变量之间的关系散点图，拟合财政补贴与企业研发投入之间的相关性，从中发现两变量之间是正向关联，即财政补贴促进了企业创新投入。这与前文的理论模型分析一致，同时也为下文经验分析提供了线索和依据。

表2 主要变量的描述性统计

图1 研发投入与企业获得财政补贴的关联

四、实证结果与分析

实证分析主要有两部分，一是基准回归估计，即从总体上估计财政补贴与企业创新间的关系；二是异质性分析，从行业、区域角度具体分析财政补贴与企业创新间的关系。

（一）基准回归结果

基准回归部分采用静态面板数据模型（包括固定效应模型和随机效应模型）对财政补贴与企业研发投入的关系进行稳健性检验。根据Hausman 检验值，p值为0.000，拒绝原假设，所以应选择固定效应模型的估计结果，而非随机效应模型，即不同企业之间存在不随时间变化的个体效应。

根据表3第（2）和第（4）列的回归结果，不难看出核心解释变量lnsubsidy的系数依然显著为正（分别为0.144 和0.034），这与前文理论分析的结果一致，也验证了财政补贴会促进企业进行研发投入的假设。

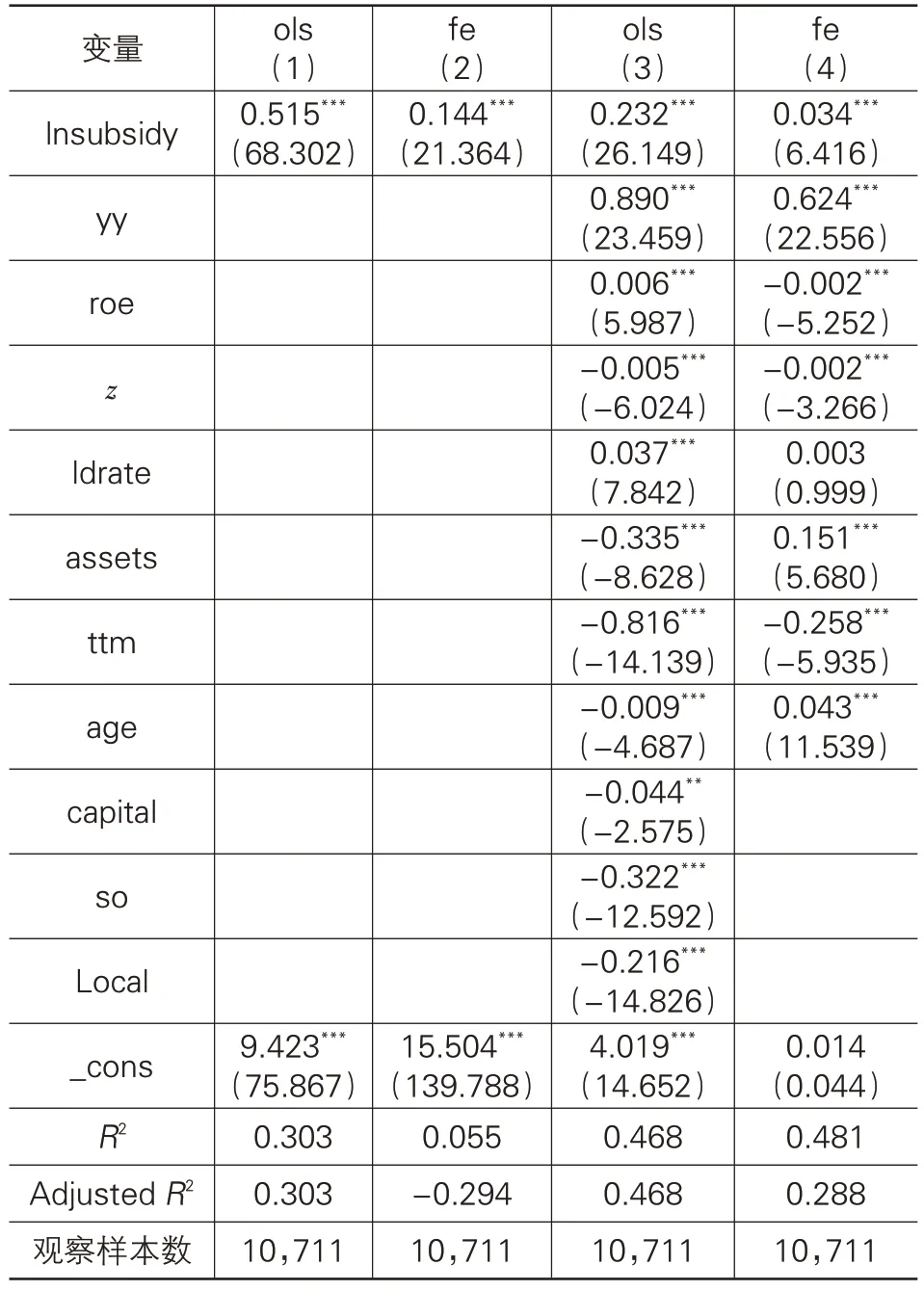
表3 财政补贴对企业研发投入金额的影响（静态面板模型）

表3 第（4）列显示的其他变量回归结果如下：①衡量创新能力的企业营业收入自然对数（yy）的估计系数显著为正，这是因为营业收入金额越大，企业的创新能力越强，从而越有动力进行研发活动；②净资产收益率（roe）的估计系数显著为负，可能是因为研发投入金额中部分计入成本费用会计科目，因而净利润与研发费用负相关，所以净利润与净资产的比例与研发投入金额呈负相关关系；③股权集中度（z）的估计系数显著为负，可能是因为股权集中在少数股东手中时，股东更偏向于风险规避，从而从事更少的高风险性研发活动；④总资产自然对数（assets）的估计系数显著为正，理由是总资产越多，企业抵御风险的能力越强，同时更倾向于长期规划，从而更有能力和动机进行研发活动；⑤总资产周转率（ttm）的估计系数显著为负，即总资产周转率越高企业研发投入金额越少，这似乎不符合常理，对此本文给出的解释是：总资产周转率反映的是企业资金从投入到产出的使用绩效，该比率越高，说明资金周转速度越快，而企业研发具有长周期的特性，因此企业研发投入与资金周转率反向相关；⑥企业年龄（age）的估计系数显著为正，本文认为可能的原因是企业年龄越大，相对企业发展越成熟，从而更有实力从事研发活动。

（二）异质性分析

财政补贴与企业创新总体表现为正向相关关系，这种关系在行业、区域上是否表现为一致性呢？为了回答此问题，本部分将分别对样本数据根据行业和区域分类做异质性分析。

1.行业异质性分析

将共计10 711个样本按照行业类别分成19组小样本进行异质性检验，根据Hausman 检验，若拒绝原假设，则采用固定效应模型，否则采用随机效应模型，并用聚类稳健标准误控制异方差问题。未列出样本量过小和回归结果不显著的行业，表4报告的是回归结果较显著的6个行业，第（1）至第（6）列分别是制造业，批发和零售业，信息传输、软件和信息技术服务业，租赁和商务服务业，科学研究和技术服务业，公共管理、社会保障和社会组织。在各个行业的回归结果中，lnsubsidy的系数均显著为正，即财政补贴均对企业研发投入具有激励效果，这与基准回归结果一致。

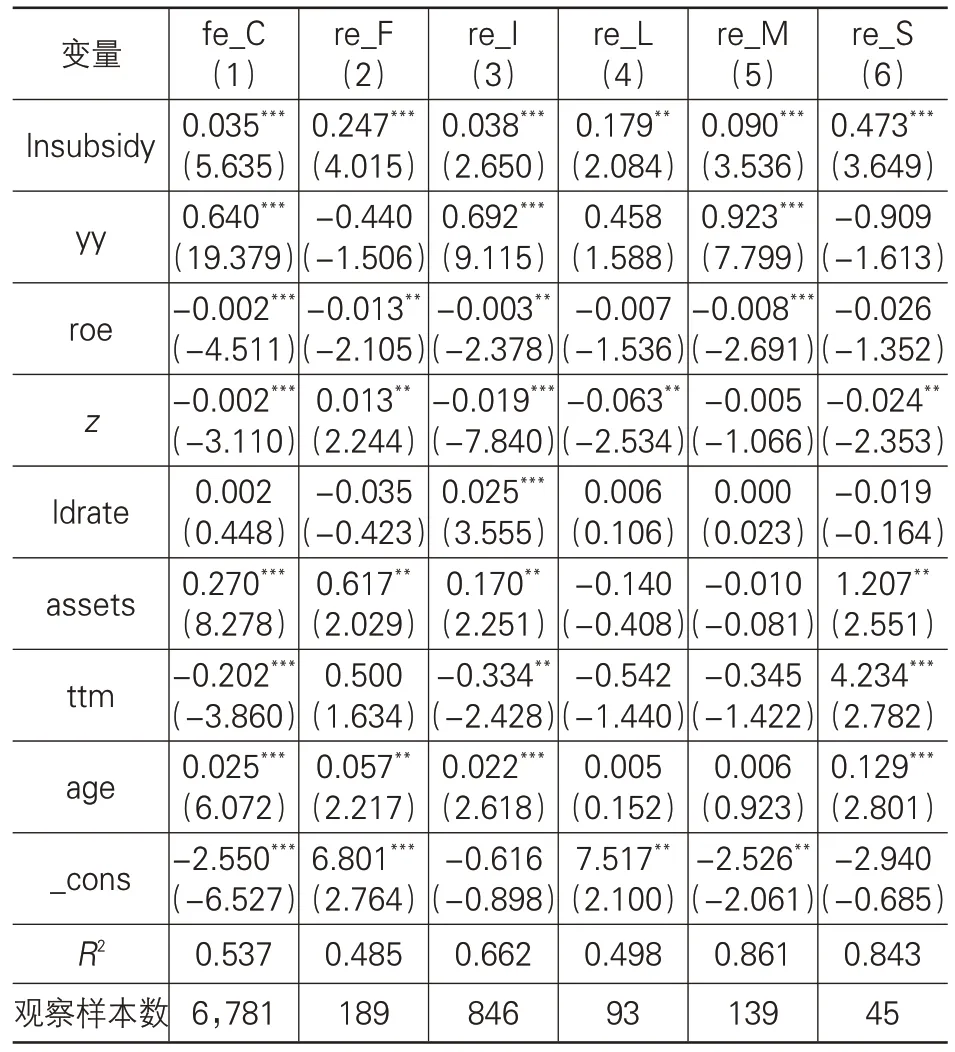
表4 财政补贴对企业研发投入的影响（分行业）

此外，还发现不同行业中lnsubsidy的系数值大小存在差异，其中第（2）、（4）和（6）列的系数值较大，说明在批发和零售业，租赁和商务服务业以及公共管理、社会保障和社会组织等行业中，财政补贴能较显著激励企业创新，这可能是因为相对于信息传输、软件和信息技术服务业等高科技企业的创新需求，前者具有较大的研发投入弹性，而财政补贴激发了企业的研发热情，具有较显著的“挤入效应”。

需要说明的是，对A股上市公司的19个行业都进行财政补贴与研发投入影响的实证检验，删除了一些样本量过少和回归效果不显著的行业样本，最终留下如上6个行业的统计结果，模型后面的字母代表各个行业的编号，编号方式来自《2017年国民经济行业分类》。fe表示采用固定效应模型，re表示采用随机效应模型，并用聚类稳健标准误解决异方差问题。

2.地区异质性分析

分地区对财政补贴与企业研发投入的关系进行实证检验，检验结果见表5 所列。具体地，根据Hausman检验值，表5第（1）至第（5)列，应选择固定效应模型，而第（6）列应采用随机效应模型，采用聚类稳健标准误控制异方差问题。

表5 的结果可以看出财政补贴激励了企业的研发投入，与前文的分析结果一致。另外，从表5第（4）（5）和（6）列可以看出,地区之间lnsubsidy 的估计系数大小存在差异，东部地区的系数最小（为0.030），中部地区的系数最大（为0.064），西部地区的激励效果居中（为0.042）。可能的原因是：由于东部地区的人力、资本资源较丰富，企业对财政补贴的依赖度较低；中部地区无论是地理位置还是发展水平都相对处在东部地区与西部地区之间，企业受所处的市场环境限制较多，主要表现在缺乏投入资金，从而对财政补贴的依赖性较强，所以补贴的激励效果更加显著；而西部地区相对落后，人口稀疏，企业发展更多受到消费市场和地理位置的限制，弱化了财政补贴的激励效果。其他变量的估计系数与基准回归结果类似。

表5 财政补贴对企业研发投入的影响（分地区）

（三）稳健性分析

为考察上述实证结果的可靠性，尝试变换实证方法对基准回归结果的稳健性进行实证检验。

表6 报告的是使用OLS 方法和动态面板数据模型（包括差分广义矩估计和系统广义矩估计）进行估计的回归结果，被解释变量是企业研发投入金额的自然对数，核心解释变量是财政补贴额（lnsubsidy）的自然对数，并且控制企业营业收入等变量。具体地，在第（1）列，只控制lnsubsidy；在第（2)和(3)列，采用动态面板模型考虑被解释变量的自相关性，加入研发的滞后一期L.lnrd，不考虑其他的变量；在第(4)、(5)和(6)列，加入其他控制变量进行检验。以动态面板模型广义矩估计的估计结果为准，OLS的结果只作为参考。由于差分GMM在进行模型估计时会将不随时间变化的虚拟变量消掉，为了解决这个问题，同时采用了系统GMM 方法进行回归。对比差分GMM 与系统GMM 的系数估计值与标准误发现，差分GMM的标准误系数更小，即其估计的系数更准确。根据Hansen 检验值（接受原假设）和残差序列相关的检验结果（AR（1）检验拒绝原假设、AR（2）检验接受原假设），可知设置的广义矩估计方程是合理的，不存在工具变量过度识别等问题，其回归结果是可信的。

从表6 中不难发现，第一，lnsubsidy 的估计系数均为正且显著，说明财政补贴对企业的创新投入具有正向激励效果。这说明基准回归结果不依赖于某种特定的计量工具，变换计量统计方法不改变实证的结论。第二，L.lnrd的系数也显著，并且均为正，说明企业研发投入具有强烈的自相关性，前一期的研发投入金额与当期的研发投入金额正相关。这说明采用动态面板模型进行稳健性检验是有必要的。

表6 财政补贴对企业研发投入的影响（动态面板模型）

五、研究结论与主要政策建议

企业研发创新活动具有强烈的正外部性，从事研发活动的企业实际收益小于社会总收益，需要政府这只“看得见的手”利用财政补贴政策弥补企业的成本，使外部性内部化。

本文基于上市公司数据的实证结果证实，财政补贴对企业创新具有较好的正向激励效应，且这种效应具有行业与区域空间上的异质性。从行业回归来看，在批发和零售业，租赁和商务服务业以及公共管理、社会保障和社会组织等行业效果好于信息传输、软件和信息技术服务业等高科技企业，具有较显著的“挤入效应”。从区域回归结果来看，中部地区企业效果最好，东部地区次之，西部地区的激励效果相对更小。

为更好地发挥财政补贴对企业创新的作用，本文提出如下政策建议：

（1）针对不同省域的企业，采取差异性财政补贴政策。针对东部地区的企业，主要采取减税降费和税收优惠的措施，改善营商环境，增强企业自身的发展活力，从源头上减少对财政补贴的依赖性，用好减税政策，提升政策效果；而对于欠发达地区，应积极运用财政补贴政策，主动提供公共服务，提升居民的生活水平，提升企业的持续经营与创新能力。

（2）针对不同的行业实施不同强度的财政补贴。逐步强化财政补贴在批发和零售业，租赁和商务服务业以及公共管理、社会保障和社会组织等行业中的作用，发挥财政补贴的“挤入效应”，对于其他诸如信息传输、软件和信息技术服务业等高科技企业行业，要引导其走市场之路，财政补贴要逐步从中退出。

（3）强化财政补贴支出绩效考核，将财政补贴资金的使用绩效与具体项目的创新绩效结合起来考虑，提升财政补贴资金的使用绩效，遏制财政补贴乱象。