水沙条件对河床纵向地形变化影响的数值模拟研究
2020-09-25常占鑫马小杰
张 超,常占鑫,马小杰
(四川农业大学水利水电学院,四川 雅安 625014 )
冲积河流的河床演变会受到诸多因素的影响,河型的成因以及转化机理一直是学界研究和关注的重点[1]。受到流域乃至全球层面人类活动的影响,河流系统的边界条件可能会发生较大的变化,特别是一些大型水利工程的建设,势必会导致下游河道水沙条件的变化,从而诱发河流的稳定性以及河型的转化[2]。例如,河流上游修建水库可以大幅提升下游的防洪标准,同时提升流域内水资源的配置和利用效率[3]。但是,下游的水沙过程和水沙条件也会发生较大的变化,而水沙条件的变化也会对河床演变造成重要影响,进而发生河型转化,对下游河道航运以及两岸居民的生活造成潜在的影响[4]。因此,水沙条件对河型转化的影响研究具有重要的理论和工程意义。基于此,文章通过建立二维水沙模型,利用数值模拟的方法对不同水沙条件下的河床纵向地形变化规律进行研究,以便为相关的水利工程设计和河道工程建设提供理论支持。
1 研究河段的选择
本次研究选择的是含沙量较大的四川某山区河道中比较蜿蜒的一段,试验模型的长度为300m,宽为200m,以模型的长度和弯曲程度为划分依据,将模型试验河段划分为14个不同的断面,本次试验选择其中的D3、D5、D7和D9断面进行研究,所有断面的横坐标见表1。

表1 试验河段断面横坐标 单位:m

(续表)
2 二维水沙模型的构建
2.1 模型的控制方程
二维水沙模型的控制方程主要包括两部分,一是二维水流基本方程,二是二维泥沙基本方程[5]。其中,二维水流方程主要由水流连续方程和水流动量方程组成;二维泥沙方程主要包括泥沙连续方程与河床变形方程,具体表达式如下所示:
(1)水流连续方程
(1)
式中,h—水位高度,m;p、q—x方向和y方向上的流速分量,m/s;ξ—压强,Pa。
(2)水流动量方程
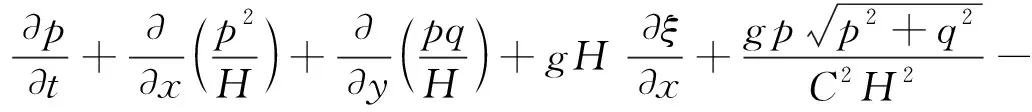
(2)
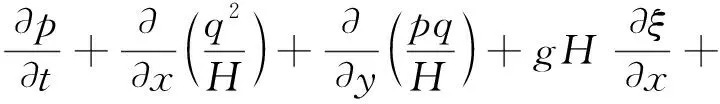
(3)
式中,H—河道水深,m;g—重力加速度,取9.8N/s2;τxx、τxy、τyy分别为有效剪切力分量,MPa;C—谢才系数;f—风阻力系数;fw—无因次风应力系数;WWx—表面风引起的x向阻力,N;WWy—表面风引起的y向阻力,N。
(3)泥沙连续方程
(4)
式中,u、ν—x方向和y方向上的垂线平均流速分量,m/s;S—水体的平均含沙量,kg/m3;c0—泥沙的扩散系数;S*—平均挟沙力;ω—泥沙的沉速,cm/s;a—恢复饱和系数。
(4)河床变形方程
(5)
式中,γ′—泥沙干容重,kg/m3;Z0—河底高程,m。
2.2 模型的建立
考虑到二维水沙模型构建的具体要求,文章以选择河段的原始地形为基础进行几何模型的构建[6]。首先以研究河段的CAD资料为基础,利用ArcGIS技术建立起研究河段的原始地形图。对构建的几何模型进行必要的概化处理,以便提升模型运算的效率和稳定性。在构建的几何模型中提取水深点数据,然后插值为地形并导入MIKE21 FM 软件,利用MIKE21 FM软件完成计算模型图的生成和网格剖分[7]。
在模型网格剖分过程中,需要对模型计算的效率和精度进行平衡。网格划分采用的是非结构三角形网格,能够较好地模拟深槽、浅滩等比较复杂的河道地形,有利于提高模型的计算精度。模型网格的尺寸在3~5m之间,最终,模型划分为1243个计算单元。模型的网格剖分示意图如图1所示。
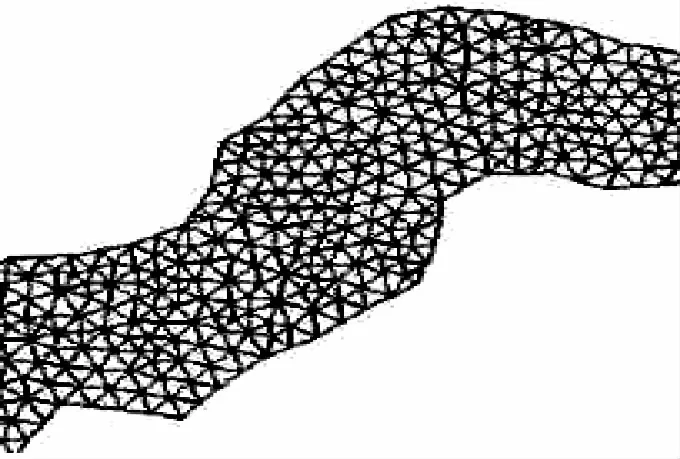
图1 研究河段网格剖分示意图
2.3 计算方案设计
研究中首先利用水流的携沙力公式计算出河道的最大挟沙力,公式如下:
(6)
式中,S—水流最大挟沙力,kg/m3;H—平均水深,m;w—水力粗度,cm/s;U—水流流速,m/s;K,m—常数系数和指数。
结合研究河段的资料,利用上述公式计算获取河道水流挟沙能力的最大值为12.0kg/m3,然后结合实际模型的尺寸以及模型的抗冲能力等因素,对水槽进水流量的大小进行设计,最终获得的计算工况见表2。
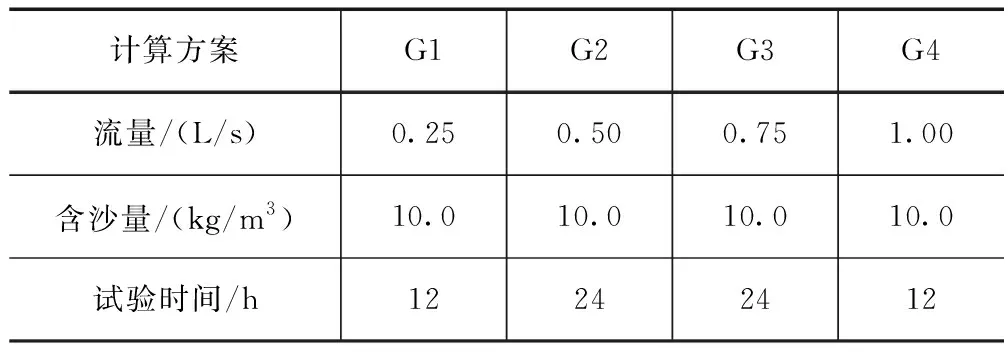
表2 计算工况设计
3 试验结果与分析
要想获取水沙条件对河道演变特征和规律的影响,首先主要获得河床的演变特征,也就是河床的纵向和横向变化特征。本次研究中,利用上节构建的数值计算模型,计算不同方案下的河床纵向变化数据,结果显示,不同方案下的河槽形状也明显不同。
3.1 G1方案计算结果与分析
利用上节构建的模型对G1方案下研究河段的河床纵向变化特征进行计算,根据模型计算获得的数据,获得不同时段的河床高程线图,其中12h河床高程线图如图2所示。由图2可知,在G1方案下,研究段的河槽随着试验时间的推移呈现出不断变宽的特征,最后阶段河槽的形态与原始河型相比已经发生巨大差异。这说明上游水沙条件的变化会对河床变形造成十分显著的影响[9- 10]。
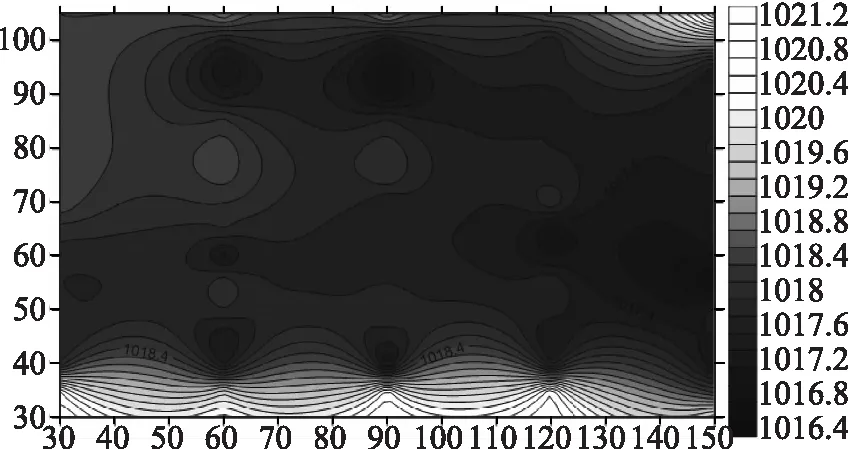
图2 G1工况12h河床高程线图
3.2 G2方案计算结果与分析
利用上节构建的模型对G2方案下研究河段的河床纵向变化特征进行计算,根据模型计算获得的数据,获得不同时段的河床高程线图,其中12h和24h的河床高程线图如图3和图4所示。由此可知,在G2工况条件下,研究河段的流量有所增大,河槽进口部位水流的总能量也明显增大,而从其对应的河床等高线图可以看出,河槽随着试验时间的推移也呈现出不断变宽的特征,本来十分蜿蜒的河道几乎变成了顺直型的河道[11]。究其原因,主要是近水口水流能量增大以后,河槽会通过变宽的方式,来消耗河槽能水流的富余能量,进而实现能量的平衡。由于研究河段河床的材料抗冲刷能力较差,产生了比较严重的河槽冲刷。另一方面,随着河槽的变宽,河槽内水流的流速会慢慢变小,水流的挟沙能力也会不断降低,水流中挟带的泥沙会沉积在河槽之内而造成淤积。随着试验时间的推移,河床也会逐渐抬高,同时河槽两侧淤积抬高的速率并不相同,右岸的河床抬高速率明显偏大。此外,随着时间的推移,河槽内出现了泥沙淤积形成的滩地,但是这些滩地星星点点,出现之后没过多久就被冲刷掉了[12]。
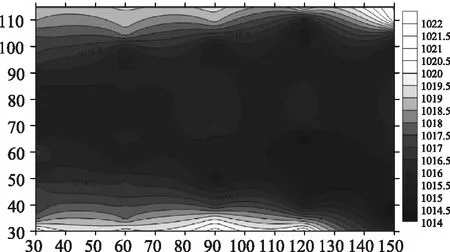
图3 G2工况12h河床高程线图
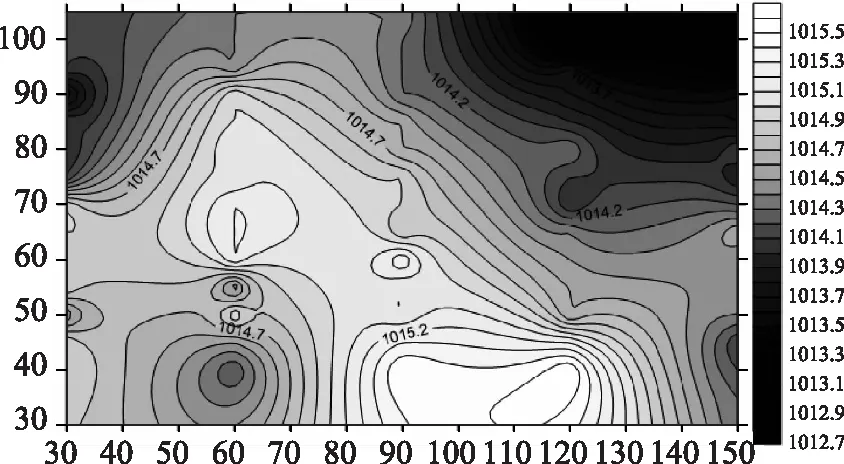
图4 G2工况24h河床高程线图
3.3 G3方案计算结果与分析
利用上节构建的模型对G3方案下研究河段的河床纵向变化特征进行计算,根据模型计算获得的数据,获得不同时段的河床高程线图,其中6h、12h、18h和24h的河床高程线图如图5~图8所示。由此可知,在G3方案下,河槽的变化呈现出更为特殊的特点。刚开始,河槽的地形变化特征与G2方案比较类似,随着试验河槽进水口流量的增加,总能量迅速增大,造成下游河槽冲刷变宽,同时河床逐渐淤积抬高。随着时间的逐步推移,河槽两岸产生了比较严重的泥沙淤积,进而形成了新的河滩,受到河滩的约束,河道的河槽又开始变窄,进而造成河槽内水流能量的不平衡。之后,河槽内由于泥沙的淤积作用形成若干面积大小不等的滩地,其中最大的一块处于河道中央,将原来的河槽一分为二,形成了两个绕流的岔道,其余的小块滩地则将河槽分为几条宽度不一的岔道。
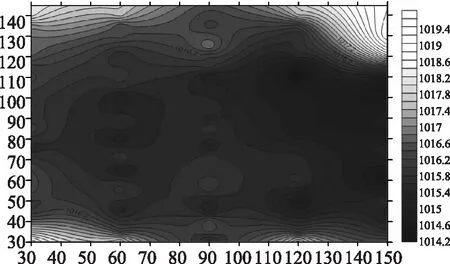
图5 G3工况6h河床高程线图
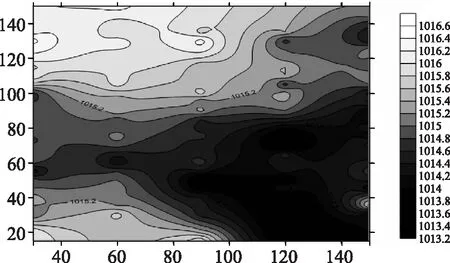
图7 G3工况18h河床高程线图
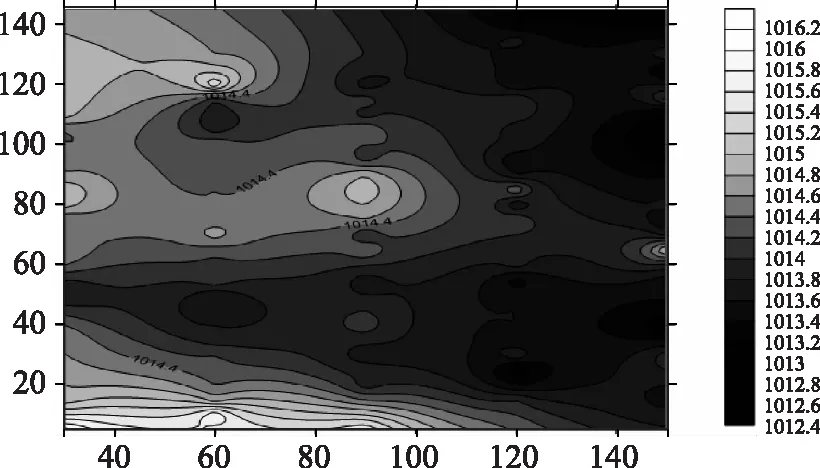
图8 G3工况24h河床高程线图
河槽内的地形特点之所以会发生上述变化,主要原因是河槽内水流的能量过大,河槽要达到能量的平衡状态,就需要通过某种方式降低河槽内水流的能量。在开始时,主要是通过对两侧河岸的冲刷作用使河槽变宽,进而增大水流的阻力,但是这也会造成水流速度降低,挟沙能力不足。因此,随着过流时间的增长,河槽内会产生大量的泥沙淤积,并在河槽中央形成大小不同的滩地,在滩地的两侧则形成了两个或多个流速的集中区域,使水流的冲刷作用继续增强。所以,随着时间的推移,河槽内形成的滩地亦被冲刷,同时在河槽内沉积形成新的滩地,并把河槽进一步划分为几个岔道,进而造成了十分显著的游荡河型特点。
3.4 G4方案计算结果与分析
利用上节构建的模型对G4方案下研究河段的河床纵向变化特征进行计算,根据模型计算获得的数据,获得不同时段的河床高程线图,其中12h河床高程线图如图9所示。由此可知,开始河槽的变化状况与前几个工况比较类似。随着进水口能量的不断增大,河槽持续被冲刷、变宽,最后形成了比较典型的顺直型河道。随着试验时间的进一步推移,两侧的河床受泥沙沉积的作用不断抬高并出现河滩,最终造成试验河段的河槽逐渐变窄、变深。
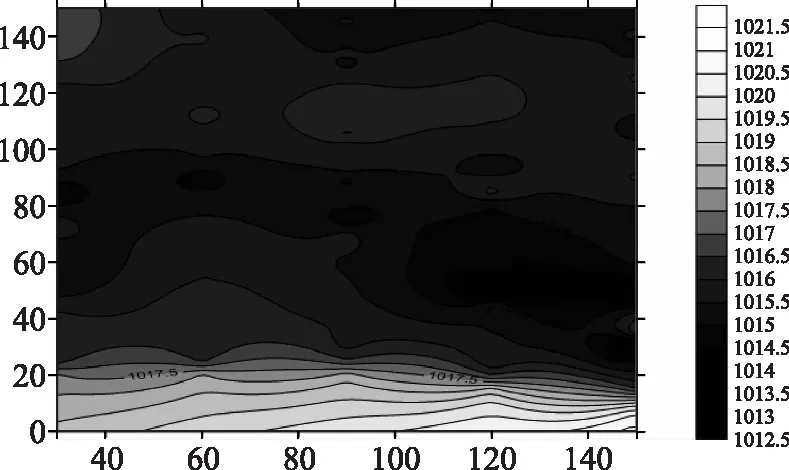
图9 G4工况12h河床高程线图
4 结论
文章通过数值模拟的方法,选择典型的山区高含沙河段,对不同水沙条件下的河道地形变化进行了研究。结果显示,蜿蜒河槽随着流量的增加,断面河宽也在逐渐变大,当流量增加到一定程度时,断面河宽变化得比较复杂,呈现出时而变宽、时而变窄的特征。在河槽的中心部位,河床也表现为时而冲刷、时而淤积的特征。如果流量进一步增大,河槽持续被冲刷、变宽,最后形成了比较典型的顺直型河道。文章的研究结论对河流上游水库调整下泄水量,通过改变下游河道的水沙条件保证下游河道形态稳定性具有重要意义。当然,本次研究河段的河床存在比较显著的易冲刷性,后续研究中需要针对各种不同性质河道进行研究,以便获得更为广泛的结论。
