川滇块体机械能与其边界带地震释放能量关系研究
2020-09-24周艺颖王云李其林
周艺颖,王云,李其林
(云南省地震局,云南 昆明 650201)
0 引 言
川滇菱形块体处于印度板块与欧亚板块中国大陆碰撞带的东南缘,是川滇地区现代断裂构造格局的核心部分[1]。李玶、汪良谋和阚荣举等人提出了川滇地区菱形块体的概念,初期称为“康滇菱形地块”[2-3]。以近北东向丽江—小金河断裂带为界,川滇菱形块体可进一步划分为川西北(西北)和滇中(东南)两个次级块体。丽江—小金河断裂带是龙门山—锦屏山—玉龙雪山构造带的重要组成部分,龙门山—锦屏山—玉龙雪山构造带将青藏高原东缘川滇地区分为两个性质截然不同的大地构造单元。20世纪70年代以来,Molnar和Tapponnier提出青藏高原侧向挤出滑移的运动图像及力学机制,为川滇地区的地壳运动提供了基本的大陆动力学理论框架[4]。现今,GPS观测结果揭示了川滇菱形块体存在平移和顺时针旋转的运动特征[5-6]。程佳认为川滇菱形块体各次级块体均受到了一种来自其相邻块体的主要应力作用而发生了旋转和南东向平移[7],刚性块体的挤出作用与重力滑塌作用并存于该区域内,下地壳“管道流”的拖拽作用是该地区刚性块体挤出抬升作用和重力滑塌的主要原因。
不同学者对该块体构造边界的认识存在一定的差异。一般认为,川滇菱形块体的边界是由甘孜—玉树断裂带、鲜水河断裂带、安宁河断裂带、则木河断裂、大凉山断裂带、小江断裂带、红河断裂带和金沙江断裂带等共同围成[8-9]。杨晓松认为地壳型块体是由大陆上部地壳所构成的“薄板”,壳内高导低速层的顶面为其底部边界和潜在的解耦带[10]。青藏高原南部—川滇地区20~35 km的深度上广泛存在低速带。大地电磁测深和地震层析成像等研究结果表明,川滇菱形块体下地壳和上地幔普遍发育低速层,这些低速层构成了川滇菱形块体的底界,使中上地壳相对刚性层得以解耦并向东南方向做水平运动[11-12]。
程佳认为刚性次级块体是区域地壳形变特征的有效简化,也是上地壳变形实际情况较为理想的模型[7]。徐锡伟认为川滇地区各级块体边界活动断裂具有一定倾滑分量的走滑断裂,表明它们的整体运动包含着平移、转动和隆升等3类构造运动[13],并讨论了块体运动的动力来源,但是未讨论块体运动所具有的能量以及这些能量和边界带地震的关系。许昭永等人将川滇菱形地块分为东南地块和西北地块,分别建立了地块应变能和时间的关系方程,结合历史强震,研究应变能积累释放与强震活动的关系。结果表明,地块应变能积累释放存在周期性[14]。
本研究在前人研究成果的基础上,依据理论力学原理,建立块体的机械能方程模型来探讨机械能、应变能和边界带地震释放能量之间的关系。
1 地块的机械能
将地块视为刚性块体,则其机械能计算式[15]为:
(1)
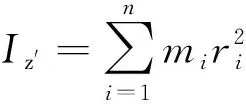

图1 块体运动的数学模型
1.1 块体的质量计算
依据质量的计算公式:
m=ρV
(2)
地块的体积依据张培震等人关于活动地块的定义、方法和中国活动构造图[16]以及刘启元等人对青藏高原东扩的地球物理学最新研究成果界定。块体密度ρ依据《地质学基础》[17]取值,为ρ=2.7 g/cm3。
2 块体边界带地震释放能量的计算
依据震级—能量关系式,由某次地震震级估算此次地震释放的能量:
Ei=1011.8+1.5M
(3)
然后把某一时间段t的某一震级以上的所有地震释放的能量相加,得到总能量,以Et表示。公式为:
(4)
3 边界带M≥6.7地震释放的能量与机械能的关系
本研究以川滇菱形块体为例,研究其运动所产生的机械能和边界带地震释放能量之间的关系。
3.1 川滇菱形块体的质量
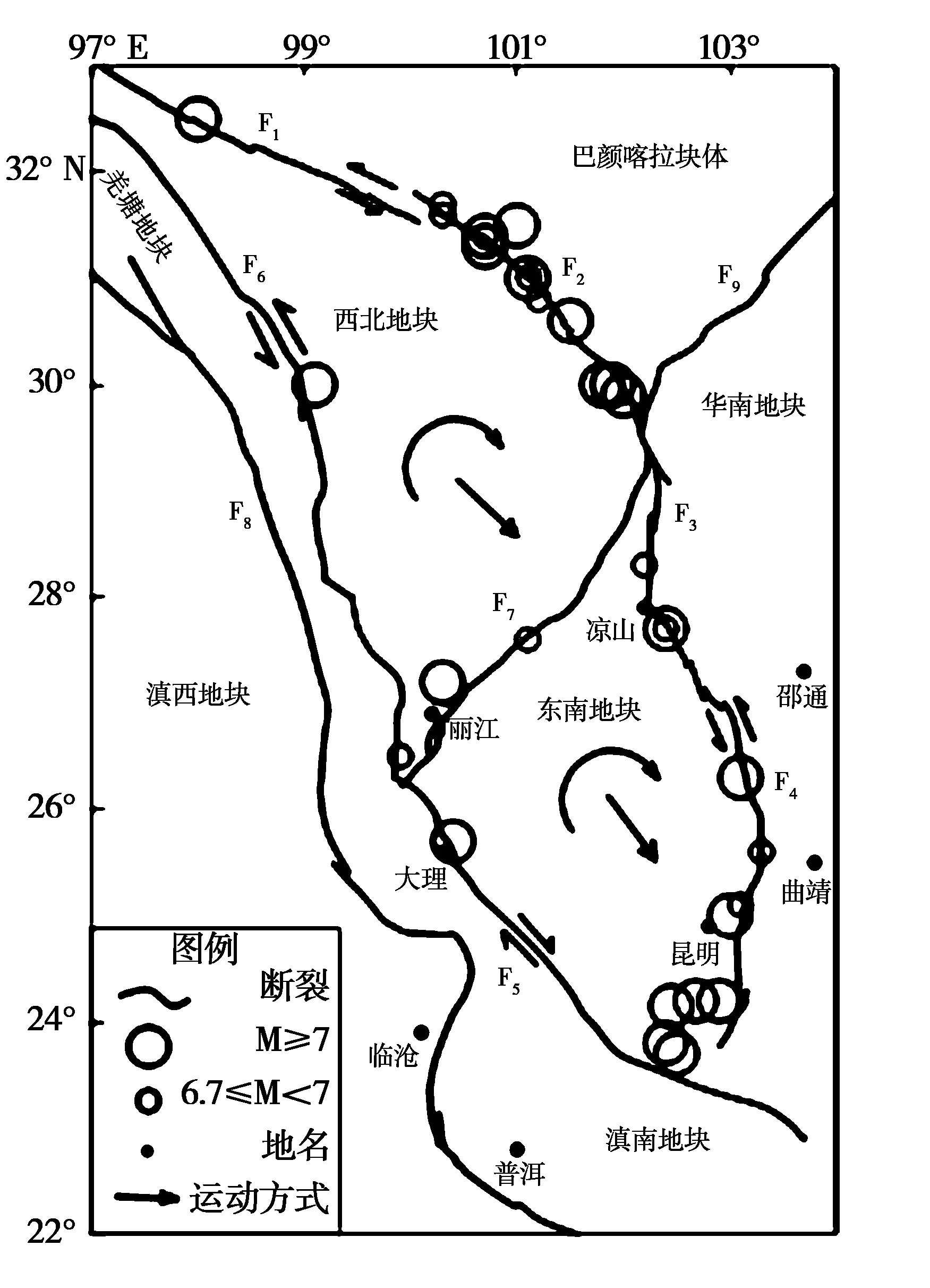
F1为甘孜—玉树断裂带;F2为鲜水河断裂带;F3为安宁河—则木河断裂带;F4为小江断裂带;F5为红河断裂带;F6为金沙江断裂带;F7为丽江—小金河断裂带;F8为澜沧江断裂带;F9为龙门山断裂带图2 川滇菱形块体边界带M≥6.7地震分布
如图2所示,川滇菱形块体被滇南、滇西、羌塘、巴颜喀拉和华南五大地块围限[18]。皇甫岗等以丽江—小金河断裂带为界,参照地壳厚度将川滇菱形块体进一步划分为两块:东南地块和西北地块。其中,东南地块面积为1.16×1011m2,西北地块面积为1.51×1011m2[19]。刘启元认为鲜水河断裂南部(康定,西藏中心羌塘地块东端)低度异常区强烈的各向异性和高电导率表明,即使与总体地壳相比,中地壳较弱,联通的延展的流动是可能的[12]。这些软弱层可能与西藏中部地区岩浆活动和流动有关。本文根据刘启元的研究成果[12],取20 km为底界,再由东南地块和西北地块的面积,算出体积分别为2.32×1015m3和3.02×1015m3。最后依据密度ρ=2 700 kg/m3,得出质量分别为:mSE=6.264×1018kg和mNW=8.154×1018kg。
3.2 川滇菱形块体的转动惯量
为了便于计算,本文将川滇菱形块之西北地块和东南地块分别理想化为两个密度均匀形状规则的刚性柱形体。因此,依据徐锡伟等人给出的半径R的数值[13],可以利用式(5)算出转动惯量,算出的结果分别为东南块体Iz′SE=1.409 4×1023kg/m2和西北块体Iz′NW=2.790 7×1023kg/m2。
Iz′=mR2
(5)
3.3 川滇菱形块体的平移动能、旋转动能和抬升的重力势能
徐锡伟认为西北地块东南向的水平滑移速率vNW=5 mm/a,顺时针转动角速ωNW=1.4 °/Ma;东南地块东南向的水平滑移速率vSE=3.5 mm/a,顺时针转动角速度约ωSE=1.5 °/Ma[20]。焦青等依据南北地震带跨断层定点水准流动水准观测数据,研究了断层垂直位移速率异常的空间分布以及震源区的逼近情况,认为通过研究断层垂直位移速率预测地震是一种可行方法[21]。张超等认为垂直形变趋势累计率在中短期的映震效果较好[22]。苏广利等认为滇西北大部分区域垂向速率为0~2 mm/a[23],与郝明给出的1~3 mm/a基本一致[24]。综合苏广利等和郝明等的研究成果,本文取西北块体的隆升速率为2 mm/a,东南块体的隆升速率为1 mm/a。
3.3.1 川滇块体的平移动能
依据公式:
(6)
取mSE=6.264×1018kg,mNW=8.154×1018kg,vSE=3.5 mm/a,vNW=5 mm/a。计算结EkSE=3.825×1013J,EkNW=10.19×1013J。
3.3.2 川滇块体旋转动能
依据公式:
(7)
取Iz′SE=1.409 4×1023kg/m2,ωSE=1.5 °/Ma,Iz′NW=2.790 7×1023kg/m2,ωNW=1.4 °/Ma。计算结果为ERSE=1.586×1011J,ERNW=2.735×1011J。
3.3.3 川滇块体的势能
依据公式:
mgH=Ep
(8)
取mSE=6.264×1018kg,mNW=8.154×1018kg,g=9.8 m/s2,hSE=1 mm/a,hNW=2 mm/a。计算结果为EPSE=6.139×1016J,EPNW=15.98×1016J。
3.4 川滇菱形块体的机械能积累
从计算结果看,相对势能而言,块体的旋转动能和平移动能远小于势能,可以忽略不计,本文只讨论块体势能和边界地震释放能量的关系。因此,式(1)就可以简化为:
mgH=Em
(9)
若把时间尺度考虑进来,式(9)变为:
mght=Etm
(10)
因为式(10)中,对于某一块体而言,mg两项近似为常数,h可正可负。h取负值时表示块体下降,释放能量;取正值时表示块体上升,积聚能量。若假定块体整体匀速抬升或下降,那么mgh项可以看作常数C,式(10)转化为:
Ct=Etm
(11)
把数据带入式(11),可得东南地块和西北地块的机械能积累分别为:
EtmSE=6.139×1016t
(12)
EtmNW=1.598×1017t
(13)
由算式可知,这是一元一次方程,表示一条单调递增的直线。
3.5 川滇菱形块体自1700年以来机械能积累
根据地震目录统计,自1700年始,川滇菱形块体边界50 km范围内共发生M≥5.0地震235次,其中M≥6.7以上有31次。但5≤M<6.7地震释放的能量是M≥6.7地震释放能量的3.5%,因为占比较小,可忽略不计,所以这里只讨论M≥6.7的地震(图2)。
3.5.1 川滇菱形块体东南地块机械能与边界带地震释放能量、应变能的关系
根据震级与能量的转化关系式(3)和式(4)分别算出东南地块边界带时间t和强震间隔时间Δt内M≥6.7地震释放的能量EtSE和EiSE。根据公式(12),算出东南块体t和Δt时间内的机械能EtmSE和ΔEtmSE。

表1 川滇菱形地块东南地块机械能和边界带M≥6.7地震释放能量的关系
由表1可知,t时间内,东南地块边界地震释放能量EtSE是其积累机械能EtmSE的0.11~1.43%;平均值为0.66%。强震间隔Δt时间内,东南地块边界地震释放能量EiSE是其积累机械能ΔEtmSE的0.08%~43.32%,均值为3.18%。机械能比地震释放能量大2~3个数量级。

表2 东南地块t时间内应变能与其边界带地震释放能量、机械能的关系
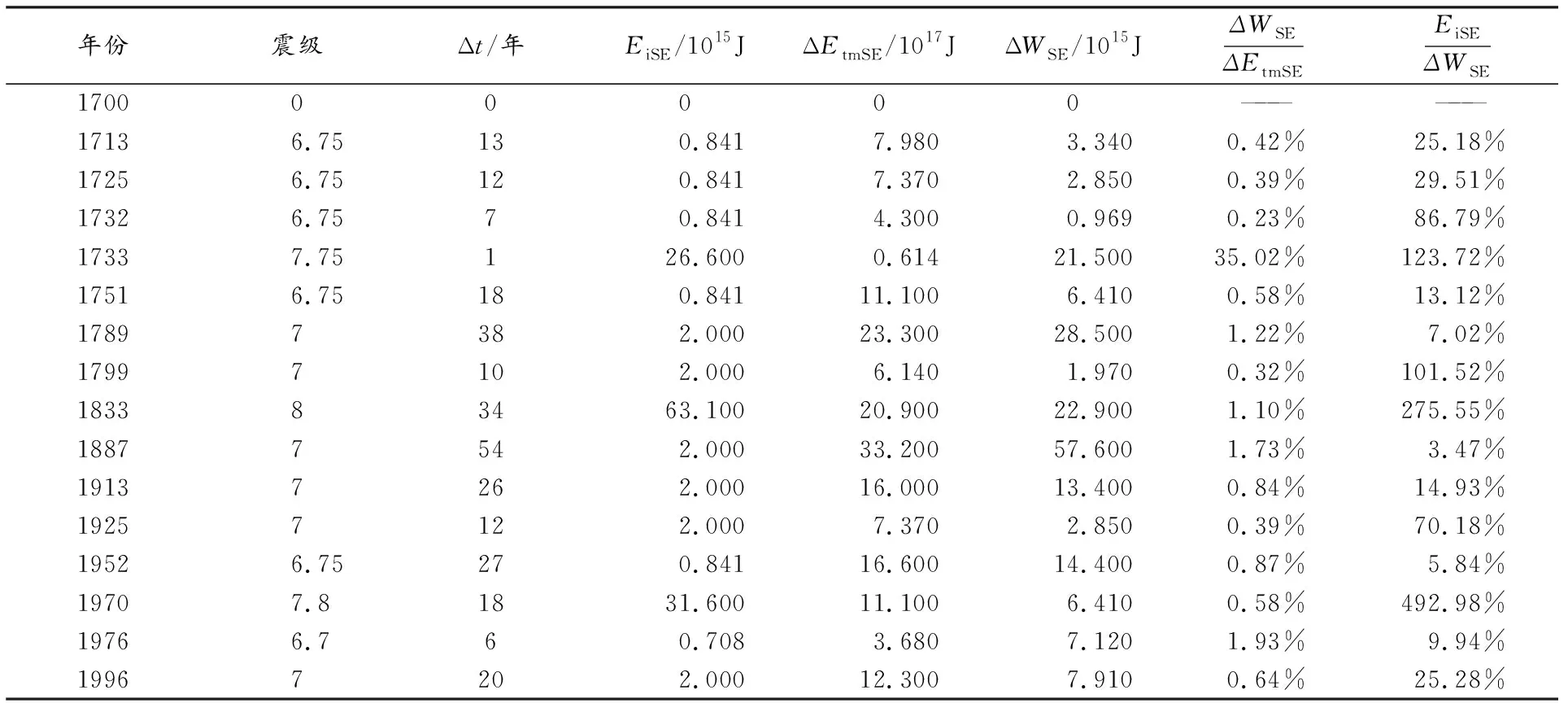
表3 强震间隔Δt时间内,东南地块应变能与其边界带地震释放能量、机械能的关系
表2、表3中,WSE为东南地块的应变能,由公式(14)[14]算出。由表2知,t时间内,东南块体边界带地震释放能量EtSE占块体应变能WSE的7.99~135.46%,均值为25.4%,有些值反映出地震释放能量反而比应变能大。块体应变能WSE占块体机械能EtmSE的0.42~9.51%,均值为4.4%。由表3知,强震间隔Δt时间内,东南块体边界带地震释放能量EiSE占块体应变能ΔWSE的3.47~492.98%;均值为85.67%。块体应变能ΔWSE占机械能ΔEtmSE为0.23~35.02%,均值为2.9%。可见,不论地震释放能量还是应变能,相对机械能的占比都很小,都在百分之几。
WSE=1.977×1013t2
(14)
3.5.2 川滇菱形块体西北地块机械能与边界带地震释放能量、应变能的关系
根据震级与能量的转化关系式(3)和式(4)算出西北地块边界带t和强震间隔Δt时间内M≥6.7地震释放的能量EtNW和EiNW。根据公式(13),算出西北块体t和Δt时间内的机械能EtmNW和ΔEtmNW,如表4。

表4 西北地块机械能和边界带M≥6.7地震释放能量的关系
由表4可知,t时间内,西北地块边界带地震释放能量EtNW是其积累机械能EtmNW的0.04~0.22%,平均为0.16%。强震间隔Δt时间内,西北地块边界带地震释放能量EiNW是其积累机械能ΔEtmNW的0.24~14.02%,均值为2.75%。可见,机械能比地震释放能量大2~3个数量级。
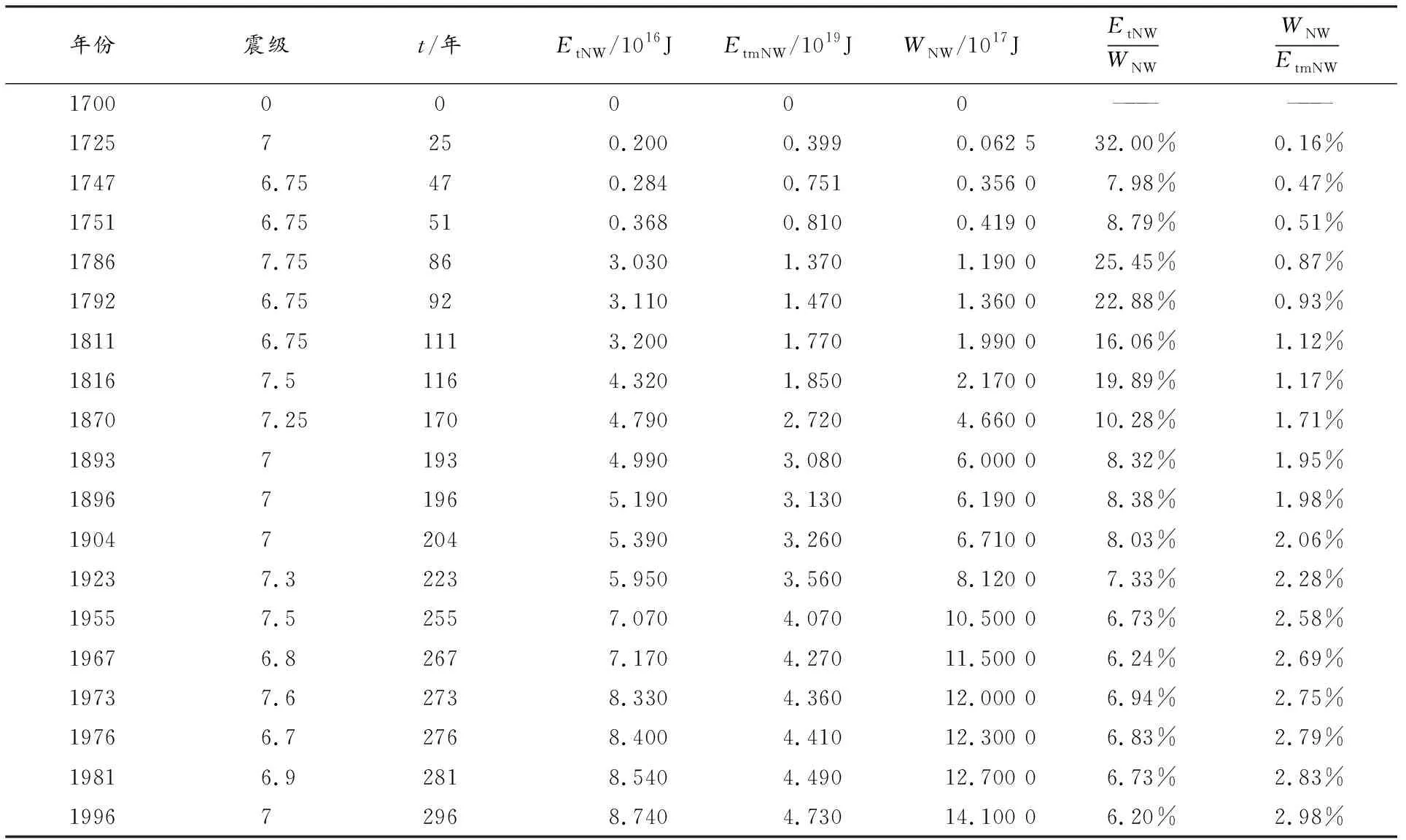
表5 西北地块在t时间内应变能与其边界带地震释放能量、机械能的关系

表6 Δt时间内,西北地块应变能与其边界带地震释放能量、机械能的关系
表5和表6中,WNW为西北地块的应变能,由公式(15)[14]算出。
WNW=1.612×1013t2
(15)
由表5知,t时间内,西北地块边界带地震释放能量EtNW占应变能WNW的6.2~32%,均值为11.95%。块体应变能WNW与块体机械能EtmNW的比值为0.16~2.98%,均值为1.77%。由表6知,强震间隔Δt时间内,东南地块边界带地震释放能量EiNW占块体应变能ΔWNW的16.11~2779.16%,均值为452.88%。块体应变能ΔWNW占块体机械能ΔEtmNW值为0.02~1.40%,均值为0.28%。可见,不论地震释放能量还是应变能,相对机械能的占比都很小,都在百分之几。强震间隔Δt时间内,边界地震释放能量与应变能的比值本应小于100%,但有些值大于100%,有些反常。
3.5.3 改造后的川滇菱形块体机械能与边界地震释放能量、应变能的关系
由以上分析可知,块体的机械能与其边界地震释放能量、应变能差距过大,说明块体的隆升坍塌并非整体性的,而是可能集中于边界断裂带20~50 km范围内,魏文薪对小江断裂带运动的观测也证实了这一点[25]。本文把东南地块面积SSE=1.16×105km2和西北地块面积SNW=1.51×105km2分别等价为圆,利用圆的面积公式求出相应的半径,再分别求出块体一侧内边界10 km和25 km范围内圆环面积,利用面积比求出圆环积累的机械能。结果数据如表7所示。

表7 等效面积计算数据
Kanamori的研究结果表明,地震效率(一次地震释放的应变能占积累的总应变能的百分比)大约为百分之几到百分之十几,其上限为18%[26]。计算应变能的时候,许昭永取15%,本文参照这一概念,取10%,即假定有10%的机械能转化为地震能。最后计算得出结果,以如下图和表表示出来。
(1)东南地块
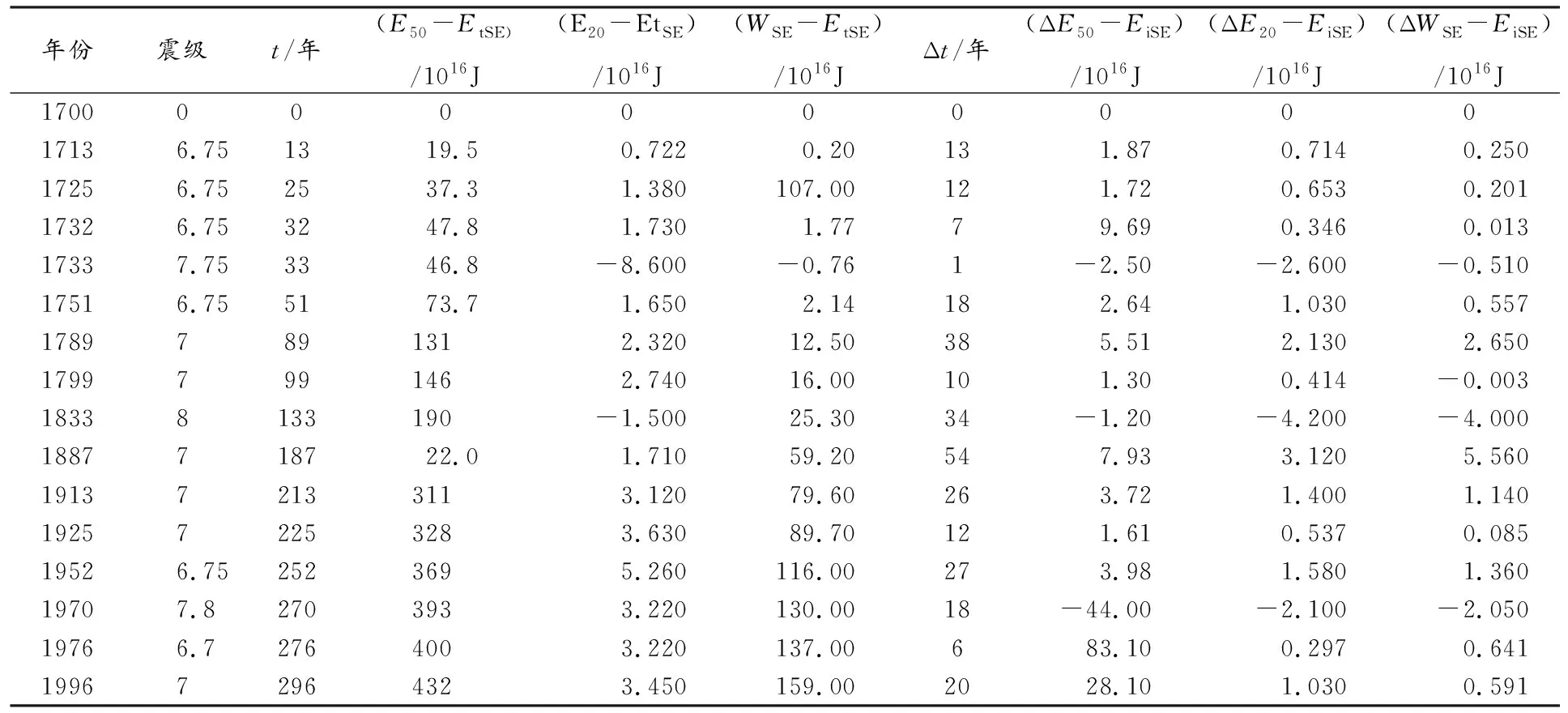
表8 东南块体边界20 km和50 km范围内机械能、应变能与边界地震释放能量之差随时间的变化
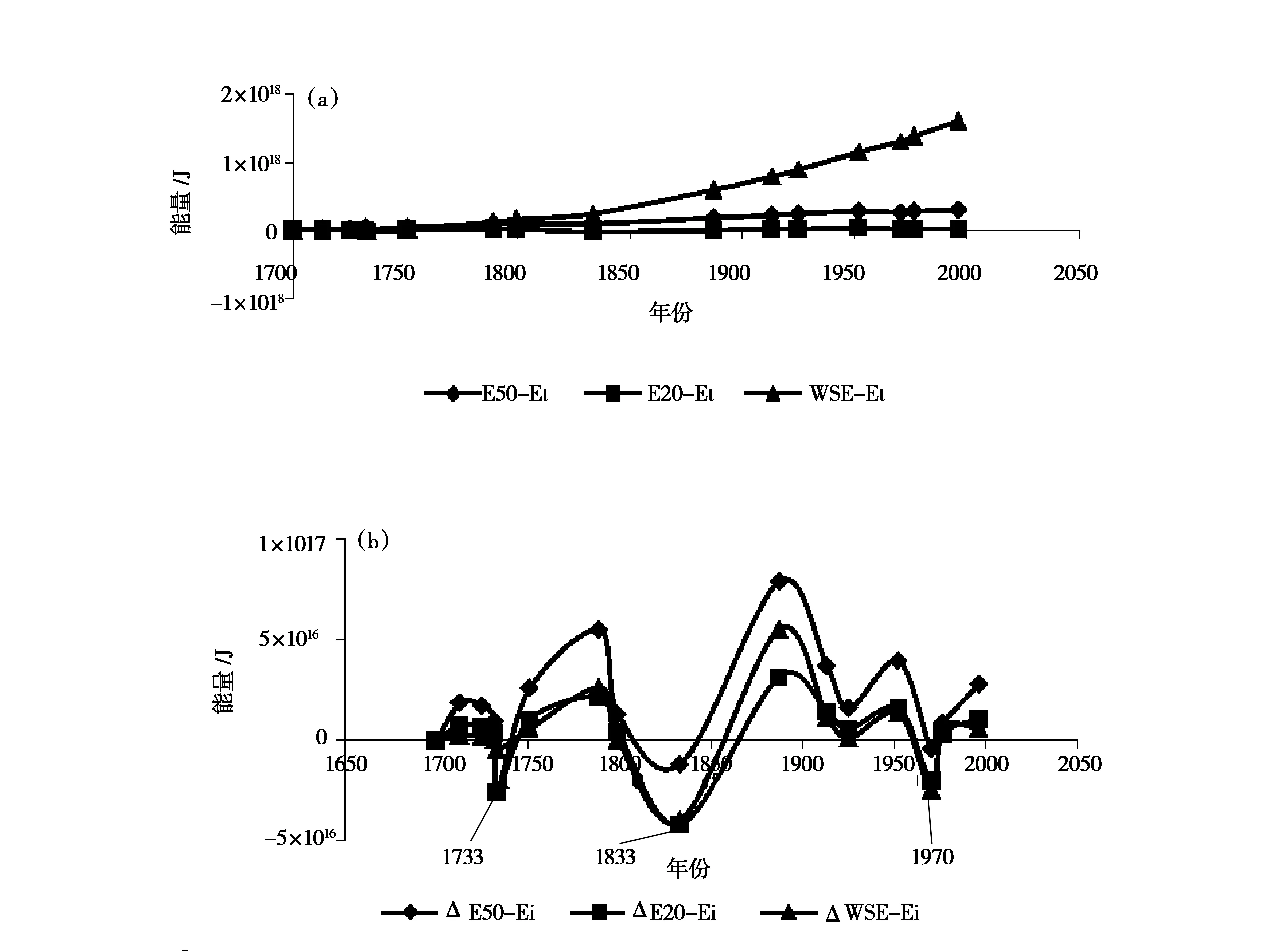
图3 随时间t变化的东南地块能量差(a)强震间隔时间Δt内东南地块能量差的变化(b)

图4 东南地块边界20 km范围内机械能和边界带地震释放能量之差随时间t的变化
由图3(a)知,块体边界20 km、50 km范围内的机械能与边界地震释放能量之差趋于一致,并且变化趋于平稳。应变能与地震释放能量的差以一元二次抛物线增长。由图3(b)知,随强震间隔时间Δt变化,机械能和边界地震释放能量之差的变化趋势与应变能和边界地震释放能量之差的变化趋势一致,但块体边界20 km范围内的机械能和地震能之差的变化与应变能和地震能之差的变化更趋于吻合。从图3(b)中也可知,20 km范围内,机械能与地震释放能量的差负值点有三个,分别为1733年、1833年和1970年。这说明1733~1833年为第一周期,1833~1970年为第二周期。图4中,机械能与地震能之差的变化更能清晰表达地震的周期性。

表9 西北地块边界20 km和50 km范围内机械能、应变能与边界地震释放能量之差随时间的变化

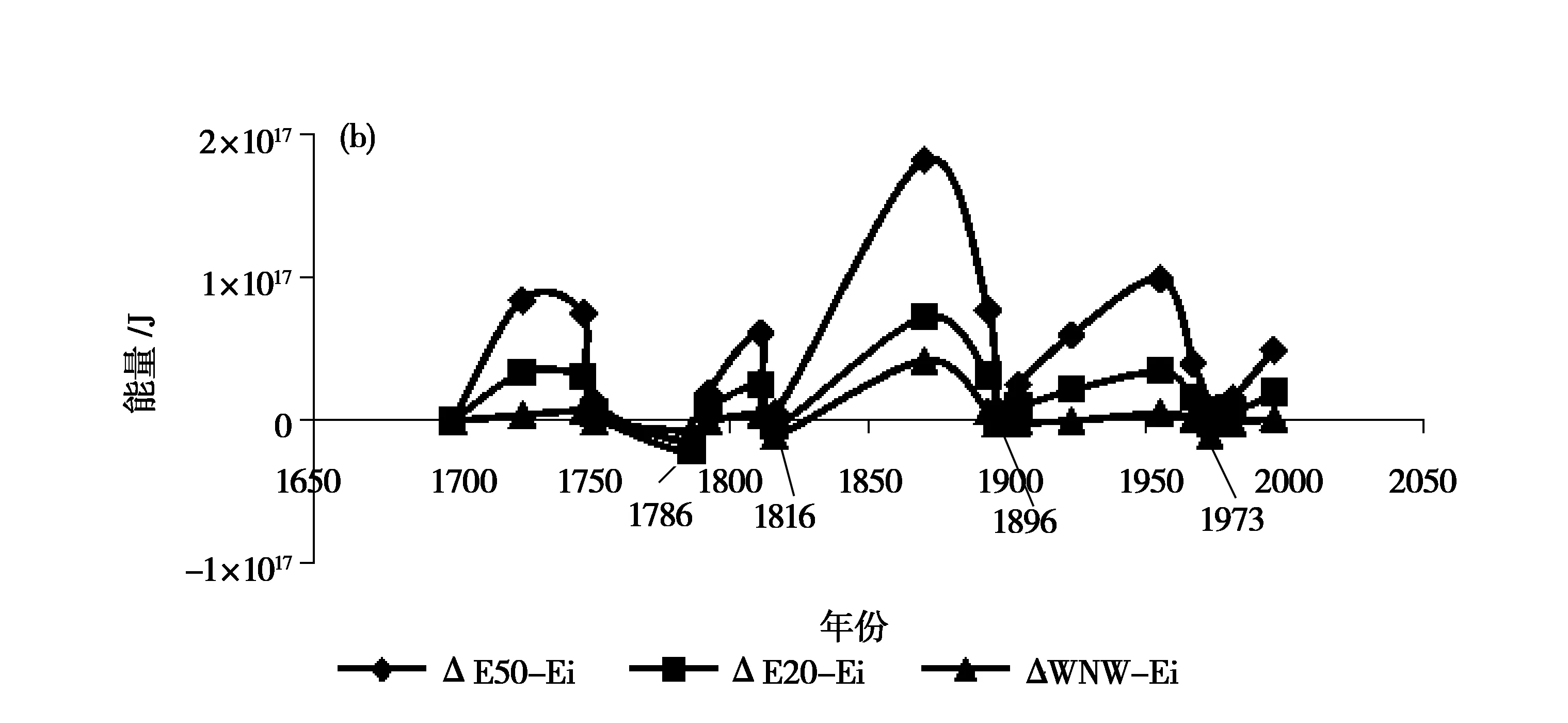
图5 西北地块能量差随时间t的变化(a)西北地块能量差随强震间隔时间Δt的变化(b)

图6 西北块体边界20 km范围内机械能和边界地震释放的能量之差随时间段t的变化
(2)西北地块
由图5(a)可知,西北块体边界50 km范围内机械能和边界地震释放能量之差与应变能和边界地震释放能量之差的变化比较吻合。20 km范围内,机械能与地震释放能量之差的变化直线斜率相对小,增长平缓。由图5(b)知,边界带20 km范围西北地块机械能和地震释放能量之差与应变能和地震能之差变化趋势较吻合。许昭永认为,西北地块的地震周期为1816~1973年,大约160年,但从图8中比较难确定这样的结果。在图6中,1816年和1973年两个点都出现了轻微能量抖动,但不似东南地块那样具有显著的规律。
4 讨论与结论
4.1 川滇菱形块体地震周期性
许昭永认为,在论及地震活动周期时,均指对某一区域的强震在时间域上所重复出现的间隔[14]。这无法从量化的角度很好地界定地震的周期性。为了讨论川滇菱形块体边界地震的周期性问题,本文尝试这样界定地震的周期:块体积累的能量与其边界地震释放能量之差远小于零的时刻在时间域上重复出现的间隔。本文利用1700年至今边界地震释放能量数据,结合根据刚体力学提出的块体机械能积累的一元一次方程模型,计算出块体机械能与边界带地震释放能量之差。利用许昭永提出的应变能积累的一元二次方程模型计算出块体应变能与边界带地震释放能量之差。对比两种不同的能量差,其随时间的变化基本一致,关于地震周期,两者吻合得比较好。但本文认为,从1700年到2000年,时间跨度过短,还不足以确定地震的周期性。特别是西北块体,地震周期的规律性不是特别明显,不能贸然断定块体的地震周期为160年。
4.2 块体积累的机械能远大于边界带地震释放能量的讨论
从本文计算出来的数据分析看,没有经过优化改造之前,块体机械能要远大于边界带地震释放能量,达到2~3个数量级。机械能和边界带地震释放能量的差是相当大的。原因一是历史地震记录存在相当多的遗漏[27],这些遗漏的地震所释放的能量无法统计。原因二是块体的整体抬升而具有的机械能并非全都对地震有贡献,只有在边界带的抬升才对地震有贡献,并且边界带的机械能也并非完全转化为地震释放的能量,而是有相当一部分转化为热能耗散了,或者是有一部分存储起来,随着地壳抬升而固化了。里德提出了地震成因的弹性回跳学说,此学说认为,由于地壳运动使岩石发生弹性形变,当变形超过一定程度时,岩石发生断裂而错动,变形以后的岩石回弹以弹性波的形式释放出应变能的过程[28-29]。地震是应变能的释放过程,是和块体储存的应变能直接相关。从许昭永的应变能方程看,应变能是时间的二次方的函数,本文提出的块体机械能是时间的一次方函数,所以应变能和机械能是相关的,也就是说,机械能大小在某种程度上可以反应应变能的大小,或者说,机械能和应变能两者间可以建立起对应关系。因此,一定程度上避开计算应变能时所做的一系列假设和确定方程参数的困难。从而另辟蹊径,创新性地利用机械能来探讨边界带地震释放能量,以及探讨机械能与应变能的关系。若从块体整体上计算机械能,得出的结果远大于应变能以及边界带地震释放的能量,鉴于块体的形变并非块体整体,而是其边界地带,大地震也多发于此边界带,因此选取边界带宽度50 km和20 km两个数值计算机械能。从得出的结果看,两者都和应变能比较吻合,但20 km范围内的结果吻合得更好一些。因此,本文认为块体的形变可能主要集中于边界带20 km范围内。
4.3 存在的问题
在计算机械能的过程中,假设了块体密度是均匀的,其合理性有些欠缺,因为地壳并非均质。在块体抬升变形的速率的取值上也有欠缺,本文取西北块体的隆升速率为2 mm/a,东南块体的隆升速率为1 mm/a,是依据公开发表的资料的平均取值,略显粗糙。如果根据边界带各断裂三维形变分段取值,分别计算机械能,然后相加,可能效果更好。但是限于已发表的数据有限,以致于计算结果也略显粗糙。如何使计算结果更精确,更科学,有待于下一步研究。本文在假定机械能转化为地震能量的能量转化效率上,也缺乏足够的科学支撑。虽然本研究尚存一些问题,但通过机械能讨论边界带地震释放能量提供了一种新的思路。
致谢:本文的地震数据来源于中国地震台网,在此表示感谢!
