做一题，通一类，会一片

徐宝华

创设情境，揭示课题——操作探究，建构模型—综合实践，应用模型—总结提升，趣味结课，构建出螺旋上升的教学环节，利用模型思想，挖掘问题的内延和外涵，力争做到“做一题，通一类，会一片”。

让学生经历将具体问题“数学化”的过程，初步形成模型思想，体会和理解数学与外部世界的紧密联系，发展抽象能力、推理能力和应用能力，这是《数学课程标准》的重要要求，这也是本单元教材的编排意图和价值取向。

数学广角的教学为渗透数学思想方法搭建了舞台，通过教学活动，让学生感受数学思想方法，学会用数学思想方法尝试解决问题，体验解决问题的策略方法。

鸽巢问题是人教版小学数学六年级下册教材第68～69页的内容。“鸽巢问题”的理论本身并不复杂，对于学生来说是很容易的。但“鸽巢问题”的应用却是千变万化的，尤其是“鸽巢问题”的逆用，学生对进行逆向思维的思考可能会感到困难，也缺乏思考的方向，很难找到切入点。

因此，用“鸽巢原理”解决实际问题时，经常会遇到一些困难。例如，有时要找到实际问题与“鸽巢原理”之间的联系并不容易，即使找到了，也很难确定用什么作为“鸽巢”，要用几个“鸽巢”。所以本堂课的教学，我们更多关注的是抽屉原理模型的建构，挖掘出隐含的问题的本质属性，从特殊拓展到一般，从而达到 “做一题，通一类，会一片”的教学价值。

所以本广角我尝试采用“创设情境，揭示课题——操作探究，建构模型—综合实践，应用模型—总结提升，趣味结课”，这样的教学设计，重在引导学生初步了解数学思想，体验数学思考，培养逻辑思维能力; 引导学生借助生活经验和直观活动建立鸽巢原理的一般化模型，增强应用意识，激发数学兴趣。

1 创设情境，揭示课题

用一副牌展示“鸽巢原理”。 （师生合作完成魔术）

师：同学们喜欢魔术吗？今天老师客串一下魔术表演，想见识见识吗？大家知道一副扑克牌有54张去掉两张王牌，剩52张，现在用它变一个魔术。这个魔术的名字叫“猜花色”。请5位同学上台每人随意抽一张牌。我猜，每位同学的手中至少有两张花色是相同的。你们相信？见证奇迹的时刻到了。请翻牌看看，老师猜得准么？

师：猜对了，给点掌声吧。老师为什么猜的那么准，想知道吗？其实这里面蕴藏着一个非常有趣的数学原理----鸽巢原理（板书课题）

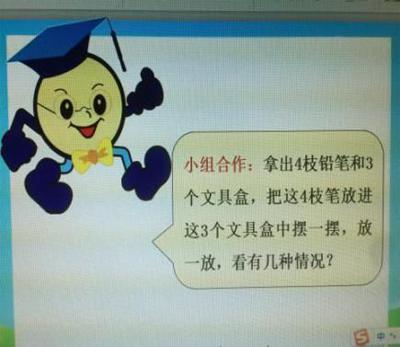
2 操作探究，构建模型

环节一：经历鸽巢问题的抽象过程，提高学生思考、推理的能力。

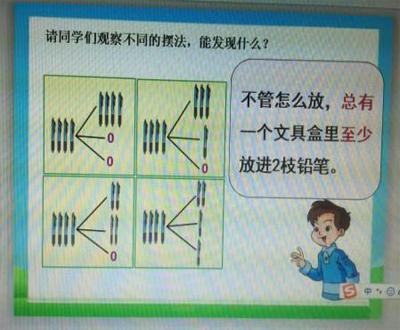
环节二：经历从具体到抽象的探究过程，建立数学模型，培养模型思想。

本阶段不但通过学生观察、概括和推理得出了至少数的算法，而且理解了特殊与一般之间的辩证关系，从而培养学生推理，分析，概括的能力。

3 综合实践，应用模型

3.1 扑克牌游戏

一副撲克牌有54张，去掉大、小王后，爸爸从余下的牌中任意抽取了14张，并对丁丁说：“这些牌里至少有一个对子”。你认为爸爸说得对吗？为什么？（点数相同的两张组成一个对子，如KK）

师：在这个游戏中，什么是物体？什么是抽屉呢？

答：13个点数是抽屉，14张牌是物体。

3.2 填一填

（1）随意找 13 位小朋友，他们中间至少有（2  ）个小朋友属相相同，（ 属相 ）是抽屉，（13 位小朋友）是物体。

（2）六年级有 385 人，至少有（2）人在同一个月过生日，（365天）是抽屉，（385人）是物体。

通过不断地和学生交流，让学生自己找出抽屉和物体，这个过程从具体到抽象，从感性到理性，从低级到高级螺旋式上升，学生小小的脑袋经历了一次数学思想方法的洗礼。

3.3 脑洞大开

4 总结提升，趣味结课

（作者单位：浙江省诸暨市城西小学）