基于多阅读器避碰的双层规划及其混合智能优化
2020-09-22张著洪
王 垚,张著洪
(贵州大学 大数据与信息工程学院,贵州 贵阳 550025)
物联网将信号感知、接入网、互联网、射频识别技术有机融合,可实现对具有信息交互功能的事物进行远程监测和控制[1]。它以无线传感器和射频识别作为底层,通过信号传送实现供应链管理、仓储盘点、目标监测、物体追踪等功能。然而,为了识别信号完全覆盖的功能区域,信号覆盖区内需部署众多共存的阅读器。此不可避免会导致多阅读器竞争共享介质,进而产生覆盖区内射频信号相互交叠或阅读器碰撞。就此,近来的研究主要集中于探讨阅读器的调度模型和高效的求解算法。在模型设计方面,代表性模型包括资源竞争分配模型[1-6]、信干噪比模型[7-8]及基于时隙的避碰模型[9-10]。此类模型中,前者是依据阅读器的优先级及边界资源竞争的建模思想而获得。陈瀚宁等[1]在阅读器不发生碰撞限制下,针对网络中频道数量、时隙分配以及处理效率问题,获得基于生物行为的射频识别模型;Roberto等[2]在多阅读器环境下,以时隙内阅读器所能覆盖的标签作为刻画网络能量损耗的性能指标,获得RFID(radio frequency identification, 射频识别)模型;文献[3,5]在文献[1]的模型基础上,以网络读写器调度的效率为性能指标,获得能满足网络读写器冲突约束限制的最小化模型;徐进[4]建立了基于资源竞争的阅读器调度任务模型,其将阅读器间的冲突转化为系统资源的竞争,借鉴操作系统的资源管理思想,给出阅读器调度问题的形式化描述。信干噪比模型是一种以阅读器的功率和干扰功率为性能指标、频率和时间为限制条件的模型,可刻画RFID阅读器在一个时间段内的识别范围。Li等[7-8]在多阅读器环境下,将信干噪比(signal to interference plus noise ratio,SINR)模型获得的阅读器覆盖范围作为性能指标,以阅读器频道的选择间隔为约束限制,获得RFID 阅读器避碰模型。基于时隙的避碰模型是在固定频率下,根据阅读器的相对位置而设计的一种阅读器分配和调度模型。Liang等[9]在假定每个阅读器仅有一个频道前提下,在时间上对阅读器的状态作严格限制,获得邻居避碰模型。
在算法研究方面,可解决阅读器避碰模型的智能优化算法大致有3种类型,即粒子群优化[3,5,10],免疫优化[7-8]以及增强学习[6]。陈瀚宁等[3]在基本粒子群算法基础上引入多种群共生的更新策略,获得能有效求解的多种群共生进化粒子群算法,其搜索效果稳定,但种群多样性有待增强。Li等[7-8]基于混合编码、资源分配策略及免疫网络原理,获得可求解避碰模型的人工免疫网络算法。该算法在确定阅读器识别范围方面优于粒子群优化和遗传算法,但获得的最佳避碰方案难以确保受干扰小、干扰大的阅读器均处于最佳状态。袁源等[6]结合RFID系统中阅读器碰撞问题自身的固有特性,利用Q-学习增强算法,获得阅读器的频率最佳分配方案。
综上,由于RFID系统下阅读器的布局涉及的约束限制较多且受干扰较为严重,使设计贴近实际的阅读器避碰模型较为困难。与此同时,此类模型常为双层或多级规划模型,导致探讨求解的算法有一定难度。为此,本文将阅读器界定为稀疏和稠密两种类型的基础上,给出双层规划避碰模型,进而探讨基于遗传算法、免疫优化和人工鱼群算法的双层混合智能优化算法(bi-level programming based hybrid intelligent optimization approach, BPBHIOA),并用于求解稀疏和稠密阅读器的最大识别半径。
1 避碰模型描述
给定长、宽分别为L1、L2的矩形内N个阅读器R1、R2、…、RN,第i、j阅读器Ri、Rj之间的欧氏距离为dij。一般地,根据阅读器之间的远近,可将阅读器划分为两种类型,即稀疏阅读器和稠密阅读器。假定阅读器的最小、最大识别半径分别为rd和rD。称阅读器Ri为稀疏阅读器,若Ri的最大识别范围内(半径为rD)至多包含两个阅读器,同时,Ri及其包含的阅读器的最小识别范围(半径为rd)之间不能交叠;否则,将非稀疏阅读器称为稠密阅读器。在此,建立阅读器避碰模型来表征各阅读器在最小识别范围不重叠前提下,最大化各阅读器的识别范围。将以上N个阅读器划分为两个集合A和B,即稀疏集A={X1,X2,…,Xp}和稠密集B={Y1,Y2,…,Yq},p+q=m。当A中阅读器的位置已知时,B中所有阅读器的最大识别面积之和即为
(1)
其中,xi和yj分别表示稀疏阅读器i和稠密阅读器j的识别半径,它们之和应不小于它们之间的距离dij,即
dij≤xi+yj,rd≤xi,yi≤rD。
(2)
另一方面,易知A中所有阅读器的识别面积之和为
(3)
于是,经由简化文[11]中刻画阅读器分布特征的性能指标,可获表征使稀疏阅读器和稠密阅读器的识别范围最大的双层规划模型(bi-level programming model, BPM):
2 算法设计与分析
2.1 免疫优化算法
免疫优化是受生物免疫应答理论启发而建立的启发式随机搜索算法,其具有局部探测与全局开采能力强、群体多样性好且获全局最优解的概率高等优点。针对目标函数为f(x)的最大化问题,基本免疫优化算法[12]的简要描述如下:
步1 参数设置:种群规模N,繁殖数M,阈值浓度σ,选择率α,突变率η,调节因子β,插入率μ。
步2 置n←1。随机生成N个抗体,构成初始抗体群An,初始记忆池Mset为空集。
步3 依据下式计算An中抗体的亲和度:
a(x)=1/(1+e-ηf(x)),0<η<1。
(4)
步4 依据选择率α,在An中选取亲和度较高的抗体构成群体Bn,且更新记忆池Mset。
步5 依据繁殖规模M,Bn中每个抗体x依据下式(5)繁殖m(x)个克隆:
(5)
步6 对于每个抗体x的克隆,依据自适应变异概率p(x)=e-a(x)实施均匀变异,获已变异的克隆集Cn,并计算克隆的亲和度。
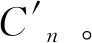
步8 依据下式
(6)
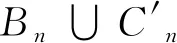
步9n←n+1。 若n小于给定的最大迭代数,则返步3;否则,输出An中亲和度最大的抗体。
以上算法具有群体多样性好、鲁棒性强的优点。比较相关的几种启发式算法,该算法的搜索效果具有一定的优势,但搜索效率受到抗体的克隆规模和抑制半径的影响较大,且算法结构有待进一步优化。
2.2 人工鱼群算法
人工鱼群算法是一种基于鱼群觅食行为特性而设计的群智能优化算法。算法步骤描述[13]如下:
步1 参数设置:鱼群规模N,尝试次数Nt,移动步长s,感知范围V,拥挤度δ。
步2 置迭代数n←1。随机生成规模为N的人工鱼群A,人工鱼i的状态为xi=(x1,x2,…,xn),xj为f(x)的决策向量中第j个分量。
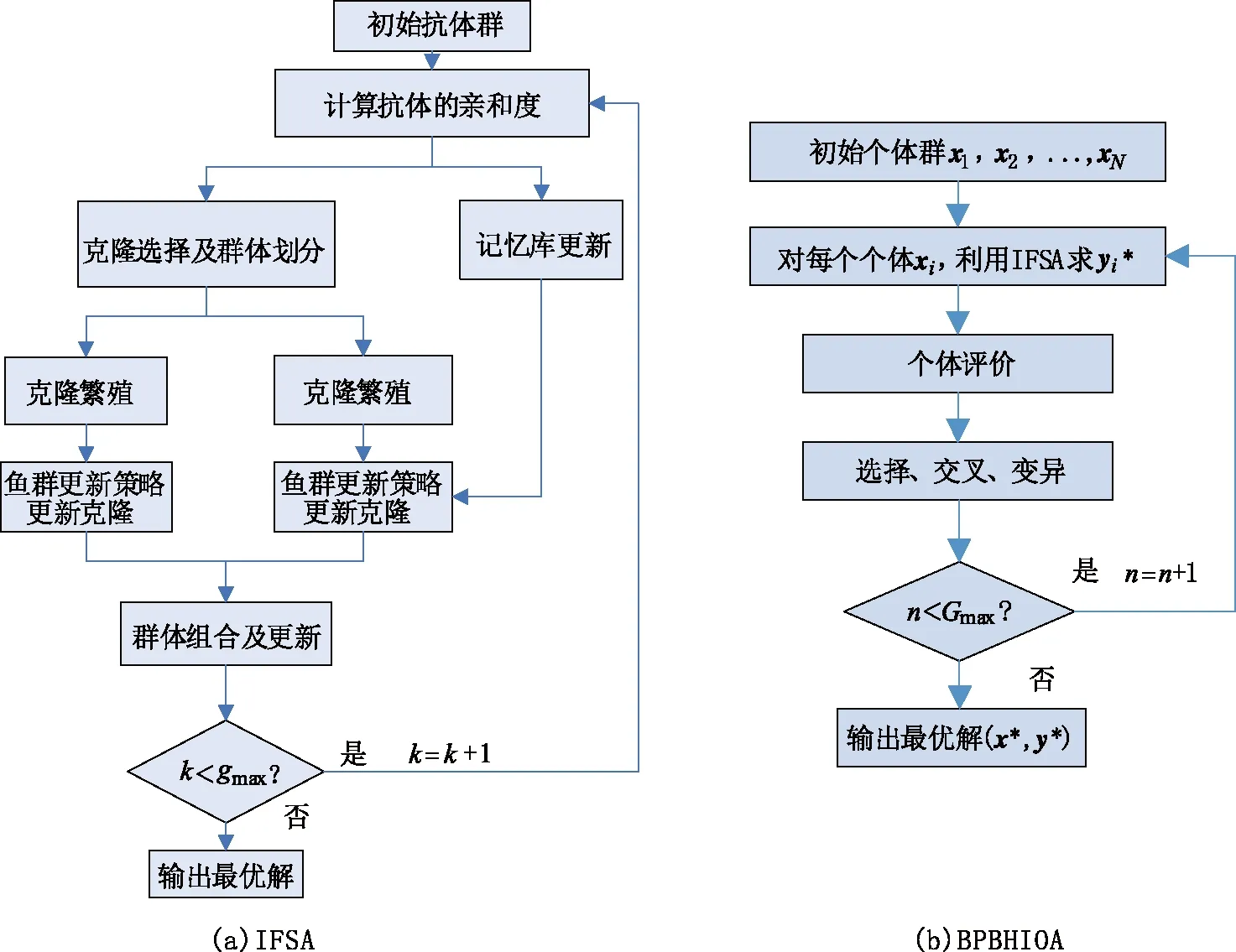
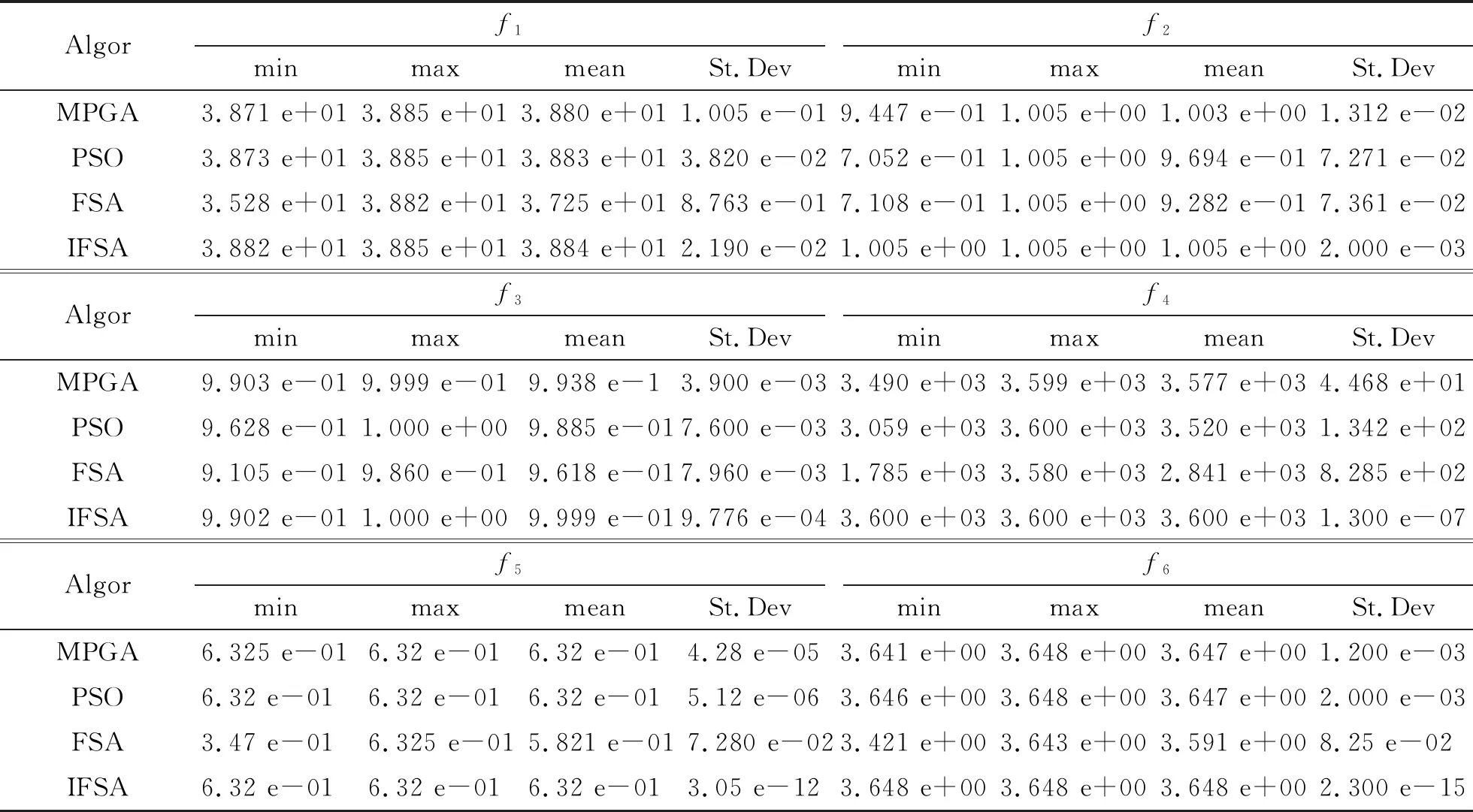
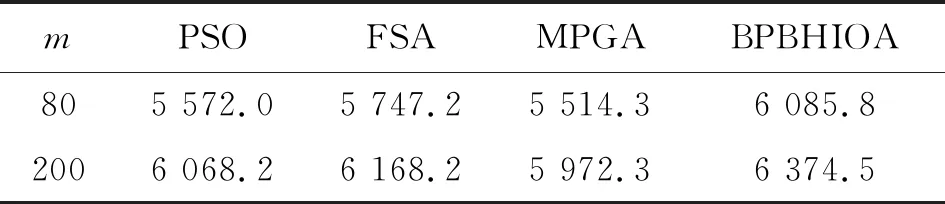
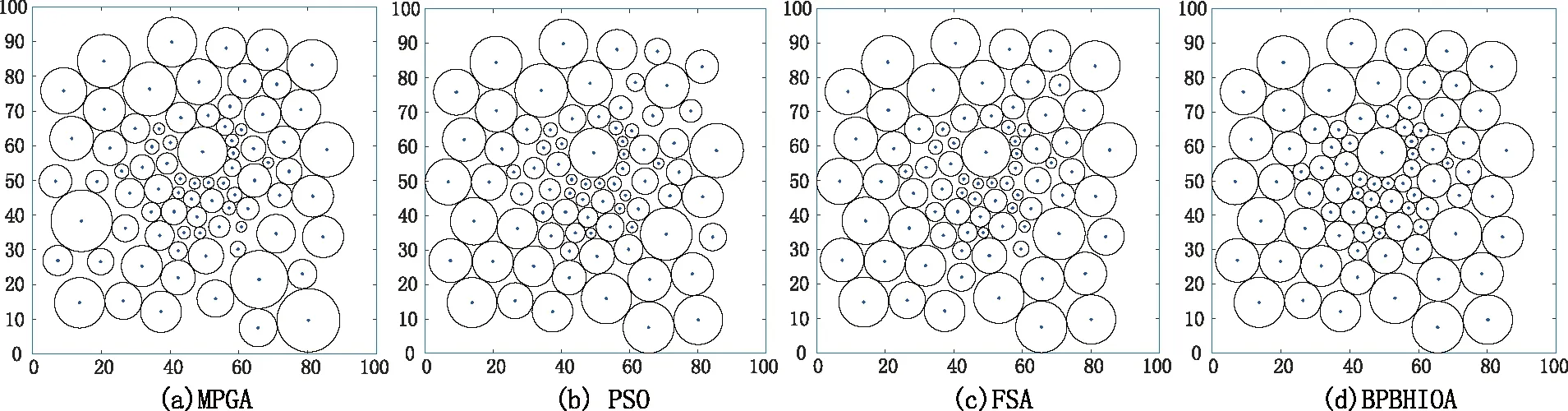
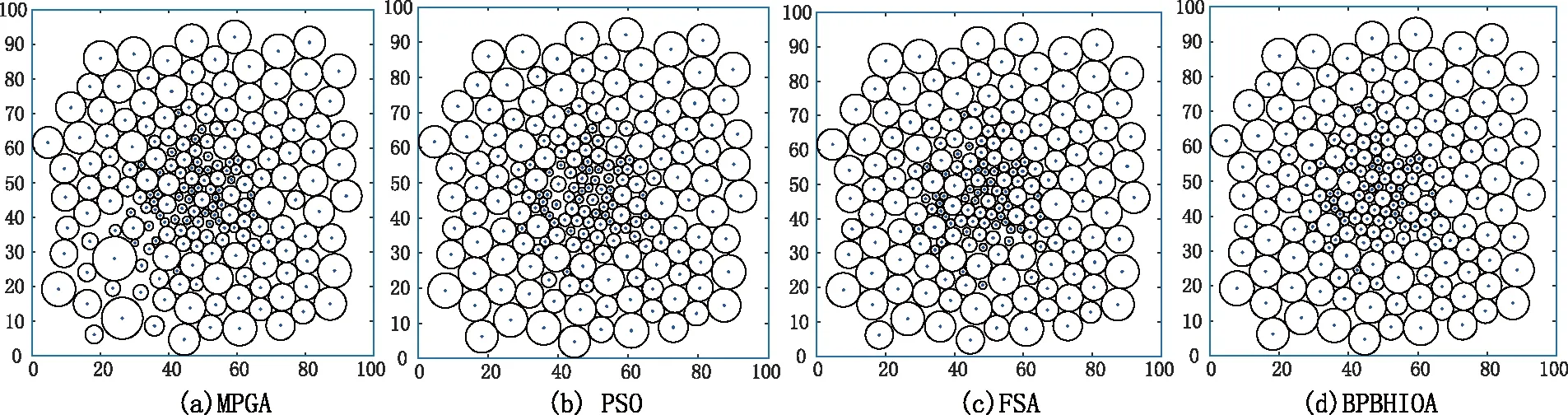
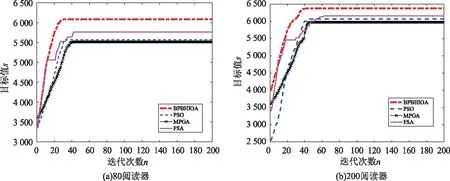
步3 觅食行为:对A中每条人工鱼xi,经由y=xi+rand()·V,在xi的感知域内随机生成人工鱼y。若f(xi)>f(y),则重复尝试至多Nt次生成y;若f(xi) (7) 由此获得的N条人工鱼x′i构成群体B。 (8) 否则,x″i←x′i。由此产生的人工鱼x″i构成群体C。 步5 追尾行为:在C中每条人工鱼x″i的V邻域内,确定其伙伴数目nf及伙伴中目标值最大的伙伴xc,进而按照步4的方式更新群体C,获得新群体D。 步6 在D中,每条人工鱼在其半径为V的邻域内,随机生成新的人工鱼更新此人工鱼,获得的群体更新当前群体A。 步7n←n+1。若n小于最大迭代数Gmax,则返回步3;否则,输出A中目标值最大的人工鱼。 以上人工鱼群算法在运行初期,由于人工鱼较为分散,步4~5的计算量较小,算法运行速度快;可是,在运行中、后期,因人工鱼过分拥挤,导致步4~5的计算量较大,从而算法的运行效率低。另一方面,算法运行后期因人工鱼过度拥挤,加之步6促使人工鱼随机游动,使得算法的收敛速度变慢且易于陷入局部搜索。 依据以上双层规划模型BPM,BPBHIOA由内、外两个寻优模块构成,算法流程图如图1所示。图1(a)是免疫鱼群算法(immune fish swarm approach, IFSA)的流程图,其作为BPBHIOA的内循环,被用于寻找BPM的各密集阅读器在满足约束限制下的最大识别半径。它是由以上免疫优化算法中的克隆选择、繁殖、记忆更新、群体更新,以及人工鱼群算法中人工鱼的位置移动策略构成的算法。此算法中,人工鱼的位置更新策略被用于增强算法的局部勘探能力和群体多样性,同时抗体的选择与更新的主要作用在于增强群体的开采能力。另外,图1(b)是以遗传算法GA作为算法框架且IFSA作为内嵌模块的BPBHIOA流程图。在此,GA由比例选择、单点随机交叉和均匀变异构成,其作用是寻找BPM的稀疏阅读器的最大识别半径。 针对模型BMP,为便于算法表述,让x和y分别表示p个稀疏阅读器及q个稠密阅读器的识别半径变量构成的向量,即(x1,x2,…,xp)和(y1,y2,…,yq),且分别被视为个体和抗体。抗体和人工鱼被视为同一说法。结合以上的算法流程图,BPBHIOA的详细步骤描述如下: 步1 输入参数的设置。GA的参数:群体规模Nout,交叉概率pc、变异概率pm;IFSA的参数:群体规模Nin,繁殖数M,更新率τ,记忆池规模m,插入率μ, 拥挤度δ,感知距离V,移动步长s, 内、外最大迭代数gmax及Gmax。 步2 置n←1。初始化规模为N的个体群P={x1,x2,…,xNout}。 步3 (算法IFSA的描述)对P中每个个体xi,1≤i≤N,执行步3.1~3.7,获取相应的最优的抗体yi*。 步3.1置n←1,Mset←φ。 初始化规模为Nin的抗体群A={y1,y2,…,yNin},计算抗体的亲和度。 步3.2依据式(5)降幂排列A中的抗体,将A等分为B、C两个种群,其中B由亲和度较高的抗体构成;在A中抽取亲和度较高的前m个抗体更新记忆池Mset,其中,m 图1 算法流程图Fig.1 Algorithm flow chart 步3.3B中各抗体依据下式计算浓度: (9) 类似地,计算C中各抗体的浓度。 步3.4确定B中每条人工鱼y在其V邻域内的伙伴数目nf及伙伴中亲和度最大的伙伴z;若c(y)<δnfc(z),则y的移动位置y′由下式确定: (10) (11) 若繁殖概率小于τ,则在记忆池中随机抽取记忆抗体y′替代y。 步3.5对C中亲和度较低的前m条人工鱼,利用记忆池Mset中的抗体按下式更新: y′=yMset+rand()·V。 (12) 其中,yMset为记忆池中随机选取的抗体。 步3.6在B∪C的亲和度较高的N个抗体中,经由比例选择挑选N-d个抗体与随机生成的d个抗体构成群体D,计算此随机生成的新抗体的亲和度,其中d=「μN⎤。 步3.7k←k+1。如果k 步4 依据yi*计算个体xi的适应度,1≤i≤Nout。 步5 群体P经由比例选择、单点随机交叉、均匀变异作用后,获规模为Nout的群体Q。 步6 对于Q中每个个体x,利用步3.1~3.7计算相应的最优抗体y*。 步7 计算Q中个体的适应度,其适应度最低的个体被P中适应度最高的个体取代。 步8P←Q;n←n+1。若n 以上算法中,步3 是算法IFSA的描述,其用于在给定一个个体(稀疏阅读器的识别半径)前提下,寻找对应的最优抗体(稠密阅读器的最好识别半径),其中步3.4需结合模型BMP的约束限制更新抗体群;步4~7是GA进化的一个迭代周期,其用于更新个体进化群。 经由以上算法的设计,BPBHIOA的计算复杂度由步3.2~3.4确定,如此3步的复杂度分别为O(Nin2)、O(N12q)及O(N12+q)。因此,该算法在最差情形下的计算复杂度为O(Nin2+N12q)。 Windows7/ CPU 3.70 GHz/RAW4.0 GB/ VC++环境下执行数值实验。为验证BPBHIOA解决BMP的有效性,首先检测其包含的算法IFSA能否有效处理一般连续函数优化问题,然后通过事例测试其能否有效确定稀疏、稠密阅读器的最大识别范围。参与IFSA比较的算法包括人工鱼群算法AFS[14]、多种群遗传算法MPGA[15]及粒子群优化算法PSO[16]。测试事例为文献[12-13]中的最大化测试函数f1—f6,其最大值依次为38.85、1.005 4、1.0、3 600、0.632 69及3.647 9。为回避随机因素对算法性能评价的影响,各算法在最大迭代数为500下独立求解每种测试问题100次。参与比较的算法的参数设置源自相应的文献。算法调试后,IFSA的参数设置是N=30,pc=0.6,pm=0.06,M=100,τ=0.3,λ=0.55,δ=0.618,d=1,s=0.2。 算法IFSA、AFS、MPGA、PSO分别求解函数f1—f6100次后,获得的统计结果如表1所示。由此表可知,相比于参与比较的算法,IFSA求解每种测试函数均能整体上获得最大的平均目标值。同时经由min、max及St.Dev的值可知,此算法的收敛精度高且搜索效果稳定。另外,MPGA比PSO和FSA获得的解质量好,且搜索效果也相对较稳定;除函数f4外,PSO比FSA获得的解质量要好,且得到的解的精度要高。通过比较此4种算法的方差获知,它们求解除函数f4外的其它测试函数均能获得次优解,特别IFSA获得的解逼近最优解的精度高。对于函数f4,IFSA具有较好的收敛性,搜索效果好,但其它算法的搜索效果的波动性较大且获得的解的质量欠理想。 在静态环境下,选取100×100的正方形区域。在此区域内随机投放的阅读器数目m取80或200。当m=80时,选取rd=1.0,rD=10;当m=200时,选取rd=1.5,rD=10。在此,将BPBHIOA中的内循环算法IFSA依次用PSO、FSA、MPGA取替之后,获得的算法也与原算法同名,并将此3种算法与BPBHIOA在此测试情形进行比较。在给定的阅读器数目下,各算法求解模型BMP获得的最好解(m个阅读器的识别半径向量)对应的目标函数值比较如表2所示。各算法获得各阅读器的识别范围及算法搜索曲线如图2~4所示。 表1 各算法求解以上6种测试问题的统计结果比较Tab.1 Comparison of statistical results of algorithm for solving the above six test problems 表2 算法获得的阅读器识别面积(目标值)比较Tab.2 Comparison of reader recognition area (target value) obtained by algorithm 由表2获知,无论阅读器的规模偏小还是偏大,BPBHIOA获得的解的目标值,即所有阅读器的识别范围的面积总和,均比其它算法获得的目标值大。此表明,该算法在人工鱼位置更新策略下,能较好地勘探具有潜在价值的解,同时算法的变异操作有助于回避约束条件的处理。其次,其它算法获得的目标值之间的偏差较小,因此它们的搜索能力较为相近。另外,图2~3表明,BPBHIOA获得的阅读器调度方案几乎能满足每个阅读器的识别圆圈(即识别范围)与多个识别圆圈相切,因此该算法的解能尽可能使阅读器之间不能被识别的区域(即闲置区域)变得窄;MPGA的解导致闲置区域较宽;PSO和FSA获得的解的质量比MPGA的高,因而产生的闲置区域比MPGA的窄。图4说明,以上算法的收敛性不受阅读器规模的影响,但收敛速度有差异。BPBHIOA易于在短时间内收敛且获得的解质量好,其它算法的进化能力偏弱,易于陷入局部搜索,导致获得的解质量偏低。 图2 m=80:各算法获得的阅读器识别范围比较Fig.2 m=80:The recognition range comparision of reader obtained by each algorithm 图3 m=200:各算法获得的阅读器识别范围比较Fig.3 m=200:The recognition range comparision of reader obtained by each algorithm 图4 各算法求解阅读器为80、200的收敛曲线比较Fig.4 The convergence curves comparison of 80, 200 reader of each algorithm 受阅读器的射频信号之间易于发生冲突的启发,研究刻画阅读器群的射频信号避碰的双层规划模型。将免疫优化与人工鱼群优化算法有机结合,得到可解决连续函数优化的免疫鱼群算法(IFSA),进而将IFSA融入遗传算法中,得到可解决阅读器避碰的双层规划混合智能优化算法(BPBHIOA)。算法的计算复杂度主要由IFSA的群体规模和稠密阅读器的规模确定。实验结果已验证,已获的阅读器避碰模型是合理的,且BPBHIOA是有效的。
2.3 双层规划混合智能优化算法
3 数值实验
3.1 标准测试问题的实验结果与分析
3.2 避碰问题的实验结果与分析
4 结论
