MCP正则组稀疏问题的稳定点分析

唐 琦，彭定涛

(贵州大学 数学与统计学院，贵州 贵阳 550025)

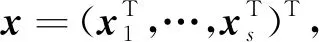
本文考虑优化问题：

(1)

其中，f:Rn→R是凸损失函数，但未必可微，惩罚项

是非凸组MCP正则项，其中

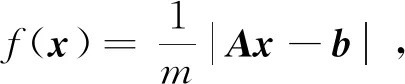
问题(1)称为组稀疏优化问题。这类问题中的变量会呈现出特殊结构，其中的零分量或非零分量会集中出现在某几个区域。所以组稀疏是先根据变量的先验信息对其进行分组，再考察各组是否为零。当ni=1,i∈Γ时，组稀疏问题(1)则退化为一般稀疏优化问题。

组稀疏优化被广泛应用于变量选择、基因表达、图像恢复和神经影像学等多个领域[1-5]。对于具有组结构的信息，使用组稀疏优化进行信号恢复，在无噪声情况下可以提高恢复的精确性，在有噪声情况下可以提高恢复的稳定性[6]。

文[10]研究了普通非光滑凸差优化问题的d-稳定点与B-稳定点，文[11]研究了非凸组稀疏优化问题的二阶d-稳定点。由于组稀疏结构和非凸惩罚的复杂性，对于此类非凸正则组稀疏优化问题的相关研究还非常缺乏。因此本文主要研究MCP正则的组稀疏优化问题的d-稳定点与critical点的具体刻画及其关系。

1 预备知识

首先给出本文将要用到的符号和概念。

令domF：={x∈Ω:F(x)<(-,]，记为是凸函数，所以f(x)局部Lipschitz连续，其Lipschitz常数记为L。

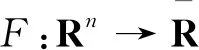
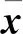
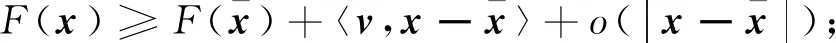
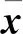
其中

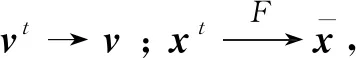
若F在x可微，则F′(x;d)=〈F(x)，d〉。

l(x)在x*的方向导数为

定义1.3(文[14],第1.2节)(广义方向导数) 设F(x)为开集S∈Rn上的局部Lipschitz函数，则F(x)在x∈S处关于d的方向导数F°(x;d)为：

一般来说，广义方向导数存在，方向导数不一定存在；若方向导数存在，则要比广义方向导数小。即

F′(x;d)≤F°(x;d)。

定义1.4(文[14]，第1.2节)(Clarke次微分) 设F(x)为开集S⊂Rn上的局部Lipschitz函数，

其中con表示凸包。

注事实上，当F为凸函数时，F在点x处的正则次微分、极限次微分、Clarke次微分均退化为一般凸函数的次微分。

最后，给出次微分的性质。

引理1.1(文[12],命题10.5)(次微分性质) 设

F(x)=F1(x1)+…+Fs(xs),

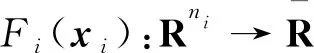
其中，

2 几类稳定点及其关系

对问题(1)给出两类稳定点：d-稳定点、critical点，给出这两类稳定点的具体刻画，并研究两者之间的关系。

首先，定义以下指标集：

Γ=Γ1∪Γ2∪Γ3。

根据文[12]练习8.27可知

(2)

其中，Bni表示ni维的单位球。

其中，

文[10]对凸差规划引进了d-稳定点的概念，下面对问题(1)给出d-稳定点的定义。

定义2.1(d-稳定点) 称x*∈Rn是问题(1)的d-稳定点，若

F′(x*;x-x*)≥0,∀x∈Rn。

下面，给出问题(1)的d-稳定点的具体刻画。

定理2.1若x*∈Rn是d-稳定点，则

其中，

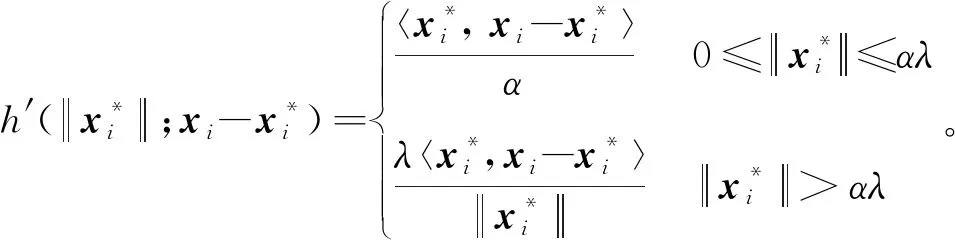
F′(x*;x-x*)

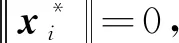
当i∉Γ1时，

当i∈Γ1∪Γ2时，

当i∈Γ3时，

证毕。

对于非光滑优化模型，critical点被广泛用于刻画模型的最优性，参见文[12,13,15-17]。下面对问题(1)给出critical点的定义。

定义2.2(critical点) 称x*∈Rn是问题(1)的critical点，若

基于问题(1)目标函数的可分结构和凸差表示，给出其critical点的具体刻画。

定理2.2若x*∈Rn是问题(1)的critical点，则

其中，

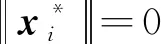
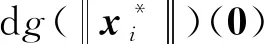
当i∉Γ1时，

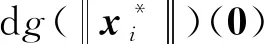
当i∈Γ1∪Γ2时，

=0;

当i∈Γ3时，

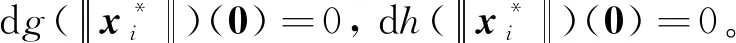
根据引理1.1可得

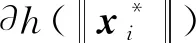
综上，即得所证。

最后，证明d-稳定点⟹ critical点。

定理2.3设x*∈Rn，若x*是d-稳定点，则x*一定是critical点。

证明若x*∈Rn是d-稳定点，则

0≤F′(x*,x-x*)≤F°(x*,x-x*)。

根据广义方向导数与Clarke次微分的关系

有0∈∂CF(x*)。根据Clarke次微分的运算性质,

∂CF(x*)

于是，

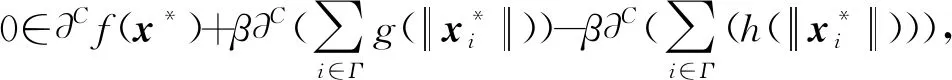
∂Cf(x*)=∂f(x*),

所以有

即x*是问题(1)的critical点。

3 最优性条件

本节讨论问题(1)的d-稳定点与局部最优解的关系，以及d-稳定点的下界性质。

定理3.1设x*∈Ω⊂Rn，若x*是问题(1)的局部最优解，则x*是问题(1)的d-稳定点。

证明若x*∈Ω是问题(1)的局部最优解，则

F(x*)≤F(x*+t(x-x*)),t>0。

所以

F(x*+t(x-x*))-F(x*)≥0。

由于t>0,两边同时除以t并取极限，则有

根据方向导数定义，可以得到

F′(x*;x-x*)≥0,

即，x*是d-稳定点。

下面给出问题(1)d-稳定点的下界性质。

定理3.2若x*∈Rn是问题(1)的d-稳定点，则

证明设x*是(1)的d-稳定点，则

由方向导数与支撑函数的关系可知，

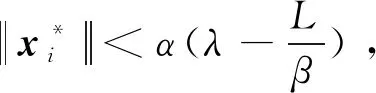
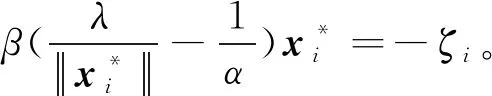
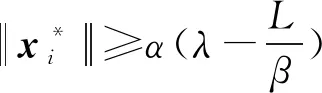
4 总结

本文研究了基于MCP正则组稀疏优化问题。对此，引进两类稳定点：d-稳定点和critical点，给出了两类稳定点的具体刻画，证明了d-稳定点⟹critical点。进一步，给出了该问题的最优性条件，即若x*是问题(1)的局部最优解，则x*是问题(1)的d-稳定点。最后得到了此模型d-稳定点的下界性质。