光学系统焦距高精度测试方法

冯晓宇 杜建祥 侯闹 董科 李文广 岳聪 张建国

（北京空间机电研究所，北京 100190）

0 引言

光学系统焦距是光学系统最基本的技术参数之一。随着空间遥感器的发展，光学系统焦距越来越长，对其测试精度的要求也越来越高[1-4]。目前，国内光学系统焦距的测量一般采用放大率法、精密测角法[5-8]和多种适用于透射式光学系统的焦距测试方法[9-14]。其中，放大率法是在平行光管焦面处放置双狭缝靶标，狭缝靶标经过被测系统成像在其焦面上，用显微系统接收图像并计算焦距，由于这种方法受平行光管焦距的限制，无法满足部分长焦距光学系统的需求；而精密测角法一般采用五棱镜和经纬仪测角，需要人工读数，并且长焦距光学系统一般只需要小角度测量，经纬仪读数误差对测试结果影响很大。国外有采用基于自准直原理的方法进行焦距测试[15]，但是定焦时采用的是刀口法定焦，存在较大误差；还有采用基于傅里叶变换的干涉法进行焦距测试，其计算复杂、操作繁琐[16-23]。

为了进一步提高焦距测试的精度，本文提出一种基于干涉仪的自准直原理焦距测试方法，该方法采用干涉仪作为点光源和被测光学系统波前采集系统，通过平面镜进行自准直，通过激光跟踪仪进行线量测量，再通过双频激光干涉仪进行角度的高精度测试，此法很好的保证了焦距测试的精度，使得焦距测试精度达到0.05%以内，为长焦距光学系统焦距测试提供了一种有效的测试手段。

1 测试原理

本文提出的焦距测试方法基于自准直原理，如图1所示：位于被测光学系统焦点位置处的点光源O发出球面波，经过被测光学系统后出射平行光，再经平面反射镜按原路反射回来，经过被测光学系统聚焦到点光源O处实现自准直过程。然后将平面反射镜旋转角度θ，为了重新满足自准直过程，点光源O将移动到点O′处，点光源移动的距离为y，则被测光学系统的焦距f为[25]

图1 基于自准直原理的焦距测试原理示意Fig.1 The basic principle testing focal length

根据式（1）可以看出，影响焦距测试精度的量分别为y和θ，对式（1）进行微分后得到

根据误差理论与数据处理[24]可以得到焦距函数f的系统误差Δf，

式中 Δy和Δθ分别为y和θ测量已知的系统误差。

而焦距函数f的极限误差δlimf为

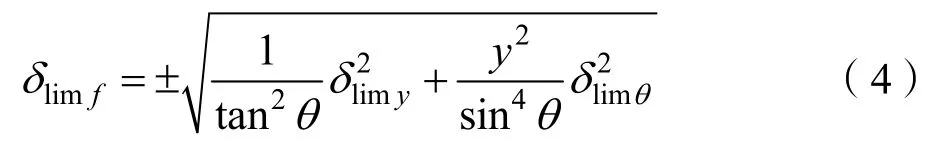
式中δlimy与δlimθ分别为y和θ测量的极限误差（即本文所说的测量精度）。

由式（3）～（4）可以看出，δlimy、δlimθ和θ的大小直接影响焦距测试的精度。当被测光学系统确定（即被测焦距f一定时），且y和θ的测量误差一定时（即δlimy与δlimθ一定），平面镜旋转角度越大，则焦距测试的精度越高（如图2所示）。

根据式（4）利用matlab仿真得到如图3的曲线。可以看出，当被测光学系统确定，且焦距测试相对误差（指焦距测试误差除以理论焦距或者多次测试得到的焦距平均值）相同时，θ的极限误差的系数远远大于y的极限误差系数这说明θ的极限误差对焦距测试精度更敏感。因此，在测试过程中要求平面镜转动角度θ的测量精度较高才能保证焦距测试的精度。

图2 焦距测试精度随平面镜转角变化Fig.2 The testing accuracy of the focal length with the variation of the flat mirror rotate angle

图3 焦距测试精度与y和θ极限误差的关系Fig.3 The relation of the testing accuracy to y and θ

2 测试方案

长焦距光学系统焦距测试方案如图4所示，主要由干涉仪、平面反射镜、双频激光干涉仪、激光跟踪仪、经纬仪、小立方镜和调节机构等组成。首先利用干涉仪作为点光源，将其放置在被测光学系统的焦点位置，这样被测光学系统出射的平行光，经平面镜原路返回即形成了干涉条纹；然后将激光跟踪仪的靶球放置于0视场焦点位置O，此时激光跟踪仪可测得0视场的焦点位置O，即利用跟踪仪的靶球代替干涉仪出射点光源的位置；接着将平面镜水平转动一定角度θ，θ可通过双频激光干涉仪及其测角配件测得，再沿X方向平移干涉仪，当再次出现同样的干涉条纹时，将激光跟踪仪的靶球放置于此时的焦点位置O′，并测得该位置，利用激光跟踪仪测得OO′的距离即为焦点移动距离y。最后根据式（1）求出被测光学系统的焦距。

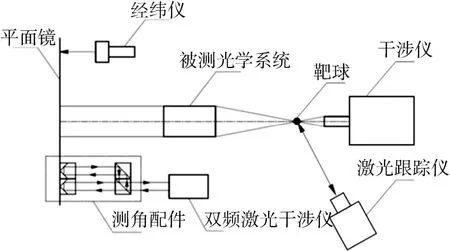
图4 长焦距光学系统焦距测试方案示意Fig.4 The focal length testing of the optical system

3 焦距测试精度影响因素分析

3.1 初始位置影响

平面镜转动的自准直光路如图5所示，图中黑色线表示平面镜未转动角度（即位于0视场）的自准直光路，蓝色线表示平面镜转动了5°后自准直的光路，红色线表示平面镜转动了 15°后自准直的光路。根据图5所示几何关系可以证明：t a n∠O1PO2=（其中O1P平行于O0O），由近轴光学原理[6]可以得到∠O0OO1=5°，∠O0OO2=15°，且被测光学系统焦距为O0O，从而得到∠O1PO2≈10.23°。

图5 平面镜转动不同角度自准直光路示意Fig.5 The auto-collimation light paths with different rotating angles of the flat mirror rotating

当平面镜初始位置位于被测光学系统 0视场时，根据自准直原理，平面镜转动 5°，点光源由点O0移动到O1，则有∠O0OO1=5°，移动距离为O0O1，那么测量焦距为同理平面镜转动 15°，则有∠O0OO2=15°，移动距离为O0O2，那么测量焦距为可以看出，当初始位置在被测光学系统0视场时，测量焦距与实际焦距一致。

当初始位置不在被测光学系统0视场，假设其在蓝色线表示的光路，那么平面镜由蓝色位置转动到红色位置转动了 10°，点光源则由点O1移动到O2，这时有∠O1OO2=10°，移动距离O1O2，那么测量焦距而实际焦距可看出此时两者有差异，设定此种情况为初始位置与0视场位置差+5°。

据此原理，假设平面镜初始位置与0视场位置差±α，平面镜转动θ，干涉仪移动距离y。那么当差+α时，测量焦距为而实际焦距为那么焦距测量误差为

而当差-α时，测量焦距为而实际焦距为那么焦距测量误差为

综合式（5）～（6），当平面镜初始位置与0视场位置差±α，其他参数与上述情况相同时，产生的焦距测量误差Δf1为

因此，为了减小焦距测试的误差，应尽量保证平面镜初始位置在被测光学系统的0视场位置。不同被测光学系统有不同的判断依据，相应的精度也有所不同，应根据具体系统具体分析采用何种手段或措施来保证。

3.2 干涉仪出射点光源位置影响

第一种情况是当平面镜转动前后，干涉仪出射光点的离焦量一致时产生的误差（如图6所示）。即干涉仪出射的点光源不在被测光学系统的焦点O0位置，而是位于焦点前O01处，与焦点的距离为+d1，当平面镜转动θ角，根据自准直原理点光源应由点O01移动到点O11处，那么测量焦距为而实际焦距为可以看出测量焦距和实际焦距有差异，设定此种情况下点光源所在位置与实际焦点位置差+d1，焦距测试误差为

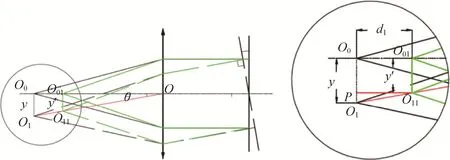
图6 有离焦量但离焦量一致时测量y产生的误差Fig.6 The location errory generated by uniform defocusing amount

第二种情况是当平面镜转动前后，干涉仪出射光点的离焦量不一致时产生的误差（如图7所示）。即干涉仪出射的点光源不在被测光学系统焦点位置O0，且平面镜转动前后点光源相对焦点的位置不一致，初始点光源位于焦点前O02处，与焦点距离为+d21，当平面镜转动θ角，点光源移动到O12处，与焦点距离为+d22，过点O12作O0O02的垂线交于点P，过点O12作O0O1的垂线交于点Q，y″为测量得到的干涉仪移动距离，那么测量焦距为实际焦距可以看出测量焦距和实际焦距有差异，设定点光源位于焦点前的距离为正（+），位于焦点后的距离为负（-），则根据几何原理得到测试误差为

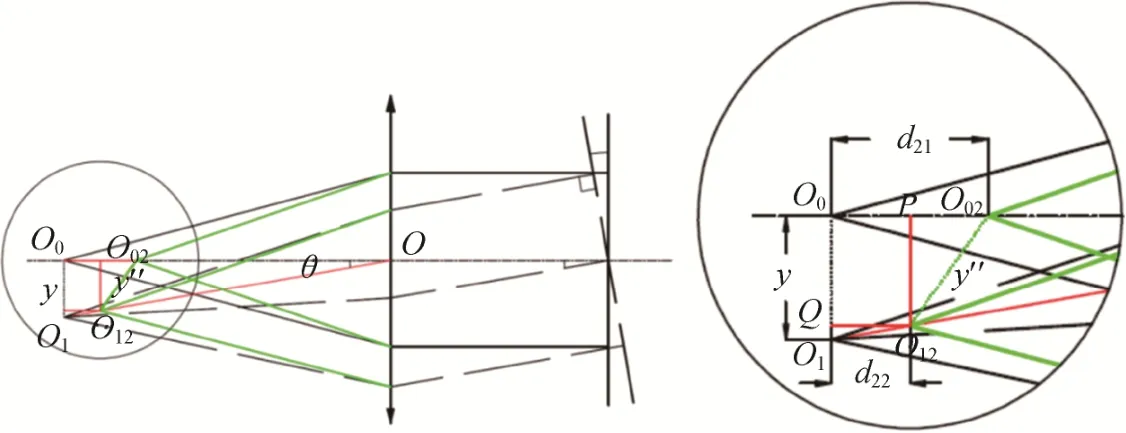
图7 有离焦量但离焦量不一致时测量y产生的误差Fig.7 The location error y generated by non-uniform defocussing amount

因此，为了减小焦距测试的误差，需要尽量保证干涉仪出射的点光源位于被测光学系统的焦点位置。保证的依据是：根据不同光学系统利用Zemax仿真计算，当所要求的焦距测试误差小于δ时可以忽略不计，则将此量δ作为光学系统焦距的失调量代入Zemax中仿真，通过计算发现将干涉仪出射点光源的离焦量（即Power）调整至小于某一波长τ时，光学系统焦距变化可忽略不计，且每次平面镜转动后重新调整光路时，Power值最好保证一致（即始终保证Power=τ）。即通过Zemax仿真计算，确定Power值调至多少时对精度的影响可以忽略不计，以此来减小此项误差。

3.3 激光跟踪仪靶球位置影响

激光跟踪仪靶球是否在焦点处对焦距测试的影响，与干涉仪出射的点光源是否在被测光学系统的焦点位置对焦距测试的影响一致。判断靶球是否在焦点位置的判据是：干涉仪不动，调整靶球位置使得干涉仪中形成由靶球返回的球心像，同时使得球心像产生的干涉条纹为0条纹，且Power值小于0.01λ（λ为波长）。那么也会产生两项误差（同图6、图7所示情况）Δf31、Δf32：

3.4 光学系统畸变的影响

对于同轴光学系统来说畸变是关于视场对称的（如图8所示）。那么此畸变对于光学系统焦距测试来说亦会引起y的测量误差（如图9所示）。如果光学系统没有畸变，平面镜转动角度θ，则平行光应该汇聚在点处O1，则点光源移动距离为y=O0O1；若光学系统存在畸变，平面镜转动角度θ，平行光汇聚在点处O2，则点光源移动距离为y′=O0O2，与没有畸变时相比，点光源移动距离相差Δy2=y-y′=-yq(θ)。因此，根据式（3）可知，由此畸变产生的焦距测试误差为

其中θ为平面镜转动角度；Δy2为畸变大小；y为理想情况下点光源移动距离；y′为实际测得的点光源移动距离；q(θ)为视场角为θ时的相对畸变。

图8 同轴光学系统畸变曲线Fig.8 The optical distortion of the coaxial light system

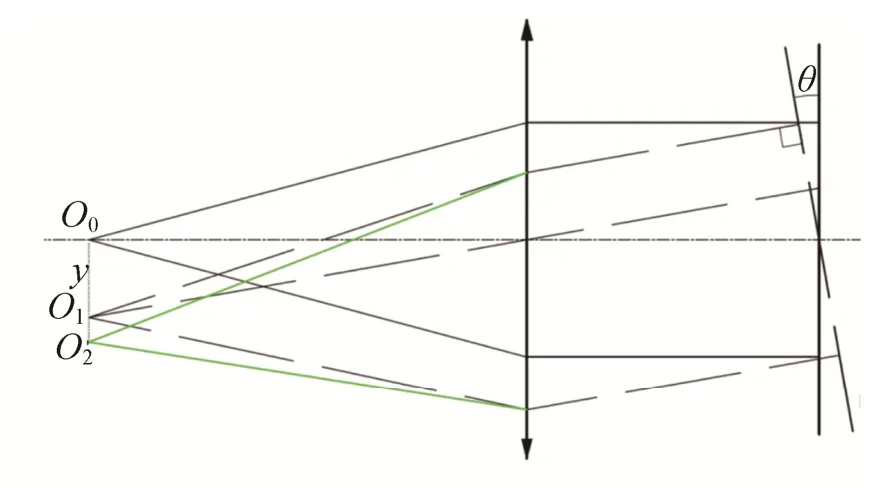
图9 由畸变引起y的测量误差Fig.9 The error generated by the optical distortion

3.5 角度测量平面和平面镜角度旋转平面夹角的影响

双频激光干涉仪角度测量误差主要是由被测件的旋转方向和角度测量方向不一致引起的。如图10所示，当角度测量平面和被测件旋转平面夹角为γ时，被测件旋转角度θ。双频激光干涉仪测角元件的有效旋转半径L′与实际旋转半径L的关系为L′=L×cosγ，此时双频激光光程的有效变化量Δx=L′×θ，双频激光干涉仪显示的角度数值应为由此可得，角度误差为：Δθ=θ-根据式（3），可得由此引起的焦距测量误差为

图10 角度测量误差引起原因示意Fig.10 The schematic of the flat mirror rotating angle testing

4 误差估计及分析

采用本文所提出的焦距测试方法对一f=10m的光学系统进行了焦距测试。以下是对采用该方法的误差估计和分析。

4.1 未定系统误差

对未定系统误差作下面几点分析：

1）初始位置不在被测光学系统0视场产生的误差。在本文试验验证过程中，根据主镜光轴引出的关系来保证初始位置在被测光学系统的0视场，采用这种方法可以保证初始位置与0视场偏差不超±10"，根据式（7），可以求得当平面镜转动±2°左右时，焦距测试误差为±1.7μm。

2）干涉仪出射点光源不在被测光学系统焦点处产生的误差。在本文焦距测试过程中，始终保证被测光学系统测试波前的Zernike像差系数中的离焦项系数小于0.02λ，根据Zemax仿真和式（8）～（9），可以求得当平面镜转动±0.2°左右时，焦距测试误差为±4μm。

3）激光跟踪仪靶球不在焦点处产生的误差。在本次焦距测试过程中，始终保证被测光学系统测试波前的Zernike像差系数中的离焦项系数小于0.02λ，根据Zemax仿真和式（10）～（11），可以求得当平面镜转动±0.2°左右时，焦距测试误差为±3.5μm。

4）光学系统畸变产生的误差。由于本文采用的光学系统的具体参数并不知道，导致其畸变函数q(·)未知，因此无法估计该光学系统的畸变对焦距测试的误差，只能通过实际的测试结果对其进行相应的分析。

5）角度测量平面和平面镜角度旋转平面不平行产生的误差。在本次试验过程中，根据经纬仪的读数可以发现平面镜在水平转动时，俯仰会有 10″以内的变化，为了排除双频激光干涉仪测量结果不是精确的平面镜水平转角，在进行焦距测试试验前，根据经纬仪的读数将平面镜的俯仰转动 10″以内，观察双频激光干涉仪的读数是否有变化，结果如表1所示，可以看出双频激光干涉仪的读数没有变化，因此可排除此项测试误差。

表1 经纬仪读数与双频激光干涉仪读数比较Tab.1 The comparison of the numerical reading between theodolite and the dual-frequency laser interferometer

4.2 随机误差

在实际测试中一般采用极限误差的形式来表示随机误差。依据式（4）可以看出，焦距的极限误差由点光源移动量y的测量极限误差δlimy和平面镜水平转动角度θ的测量极限误差δlimθ组成。由测试过程可知，影响点光源移动量y的测量不确定度有2个：1）空气扰动、环境影响以及平台晃动引入y测量的不确定度Δy1，Δy1=±1μm；2）激光跟踪仪的测量精度Δy2，Δy2=±15μm。以上两个量独立不相关，则y测量的极限误差δlimy为

影响平面镜水平转角的测量不确定度也有2个：1）空气扰动和平面镜晃动导致的θ测量的不确定度Δθ1，Δθ1≈0°；2）双频激光干涉仪测角精度 Δθ2，Δθ2=±0.1″。由此可知，θ测量的极限误差δlimθ为

根据试验数据，平面镜水平转动角度θ=0.2°，干涉仪移动距离y=34.9mm。将式（14）、（15）代入式（4），可以算得焦距测试的极限误差δlimf=±4.307 4mm，其中由于y测试误差单独引起（即令θ测量的极限误差为0）的焦距测试极限误差而由于平面镜角度θ测试误差单独引起（即令y测量的极限误差为0）的焦距测试极限误差

4.3 焦距测试总误差

由于以上误差分量独立互补相关，合成后可得焦距测试总误差Δf，

根据式（16）可算得Δf=±4.3074mm。若以表2中12次焦距测试的平均值10 006.4mm作为被测光学系统焦距的真值，则根据分析得到的焦距测试的相对误差为与实际测试结果相差不多，可以看出影响焦距测试误差的主要是干涉仪移动距离y的测试误差和平面镜转动角度θ的测试误差。

5 试验验证

为了验证本文提出的测试方法的可行性和正确性，采用了2个现有的光学系统来进行试验验证，其中一个光学系统参数为：焦距f=10m，通光直径D=650mm。对此光学系统焦距的测试结果如表2和表3所示。

表2所示数据为平面镜转动±0.2°左右时被测光学系统的焦距测试结果。这12次焦距测试的平均值为10 006.4mm，其标准差为1.458 5mm，根据误差理论可以知道表2测试结果平均值的极限误差应为那么测试的相对误差为4.373×10-4。从表2还可以看出平面镜水平转动-0.2°左右时，测得的焦距平均值较小为 10 005.4mm；而平面镜水平转动+0.2°左右时，测得的焦距平均值较大为10 007.3mm。

表3所示数据为平面镜转动不同角度时被测光学系统的焦距测试结果。可以看出，平面镜水平转动角度从-0.5°到+0.5°时，焦距测试结果相差很少，因此在调整台调量允许的情况下，选取合适的平面镜旋转角度进行焦距测试。

表2 平面镜转动0.2°左右焦距测试结果（f=10m光学系统）Tab.2 The testing results of the focal length with the flat mirror rotating angle of 0.2°

表3 平面镜转动不同角度焦距测试结果Tab.3 The testing results of the focal length with different rotating angle of the flat mirror

在吸取了10m焦距光学系统的测试经验后，为了提高测试的精度和效率，对另一个焦距为20m左右光学系统进行焦距测试时，选取了光洁度更高的跟踪仪靶球，以便能更准确的定位干涉仪的出射光点，选取了调整范围更大、调整精度更高的调整台对平面镜和干涉仪的位置进行调整。测试结果如表4所示。

最终测试结果得到12次焦距测试的平均值为20 009.6mm，测试标准差为3.215 1mm，测试的相对误差为4.8203×10-4，达到了焦距测试误差在0.05%以内的精度要求。根据第二次焦距测试发现，最好将被测光学系统和测试所用的仪器部件都放在同一隔振平台上进行测试，会更有利于保证焦距测试的精度。

表4 平面镜转动角度为0.2°左右焦距测试结果（f=20m光学系统）Tab.4 The testing results of the focal length with the flat mirror rotating angle of 0.2°

6 结束语

本文提出了一种基于干涉仪自准直原理的长焦距光学系统焦距的测试方法，用干涉仪出射的点光源对被测光学系统的焦点位置进行定焦，用双频激光干涉仪来测量平面镜转动角度，再利用激光跟踪仪测量干涉仪出射点光源的移动距离，最后根据公式计算得到被测光学系统的焦距，从而实现光学系统焦距的高精度测试。此方法为长焦距光学系统焦距的高精度测试提供了一种有效的手段。为了验证此方法的可行性和有效性，分别对焦距为10m、20m左右的光学系统进行了焦距测试，测试结果和误差分析表明焦距测试相对误差在 0.05%以内。此方法可以在光学系统进行系统像质装调的过程中，不改变现有光路的情况下进行焦距测试，可以对焦距进行实时检测，有效的减少了光学装调的时间，提高了光学装调的效率。