理清思路,志在必得
2020-09-21刘佳
刘佳
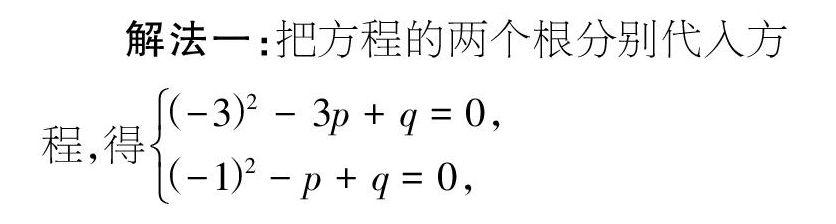

“一元二次方程”安排在九年级上册第一章,是初中阶段学习的最后一类方程,同时也为后面二次函数的学习做了铺垫。在学习一元二次方程时,我们的研究路径一般是“概念—解法—应用”。一元二次方程与之前所学的方程又有不同之处,即一元二次方程的根与系数的关系作为每年中考必考知识点,简单,易得分。下面围绕这个知识点介绍几种类型的题目,希望同学们能熟练运用。
例1 已知关于x的方程x2-6x+m2-3m-5=0的一个根是-1,求方程的另一个根和m的值。
【分析】這道题方法不唯一,你是怎么思考的?
方法一:把X=-1代入原方程,得到关于m的一元二次方程。求出m的值,再代入原方程求解。该方法没有用到一元二次方程根与系数的关系,仅利用解一元二次方程解决的。
方法二:由题意,可知a=1,b=-6,c=m2-3m-5。由一元二次方程的根与系数的关系可得x1+x2=-b/a=6,x1·x2=c/a=m2-3m-5,寻求到突破口,解决问题。
解法一:把X=--1代入原方程,得1+6+m2-3m-5=0。
整理,得m2-3m+2=0。
解这个方程,得m1=2,m2=1。
把m1=2代入原方程,得x2-6x-7=0。
解这个方程,得x1=-1,x2=7。
所以方程的另一个根是7,m的值是1或2。
解法二:由题意,得a=1,b=-6,c=m2-3m-5。
x1+x2=b/a=6。
把x=-1代入,得另一个根为7。
由x1·x2=c/a,得
m2-3m-5=-1×7=-7。
解这个方程,得m1=2,m2=1。
所以方程的另一个根是7,m的值是1或2。
例2 已知关于x的方程x2+px+q=0的两根为-3和-1,求p、q的值。
【分析】方法一:把两根分别代入原方程,得到关于p、q的二元一次方程组,解这个方程组即可。
方法二:由题可知a=1,b=p,c=q,由一元二次方程的根与系数的关系可得x1+x2=-b/a=-p=-4,x1·x2=c/a=q=3,进而求解。
