关于一类新型Dedekind和的混合均值
2020-09-21王晓瑛宋亚飞
数学杂志 2020年5期
王晓瑛,宋亚飞
(西北大学数学学院,陕西 西安 710127)
1 引言与结论
设k为正整数,h为任意整数.经典Dedekind和的定义如下
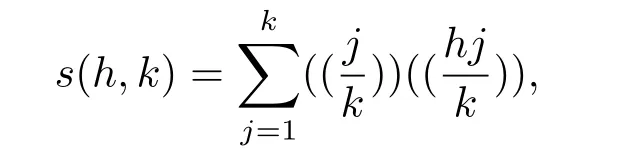
此处
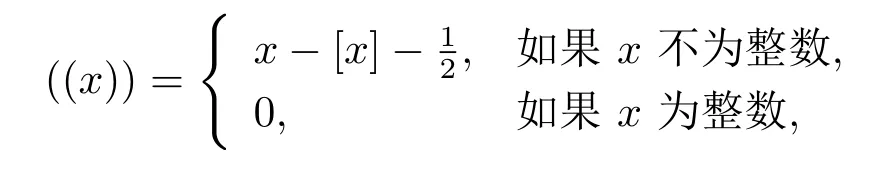
其中[y]表示不超过y的最大整数.
关于Dedekind和的最重要的性质,是互反公式.即对于互素的正整数h和k,有
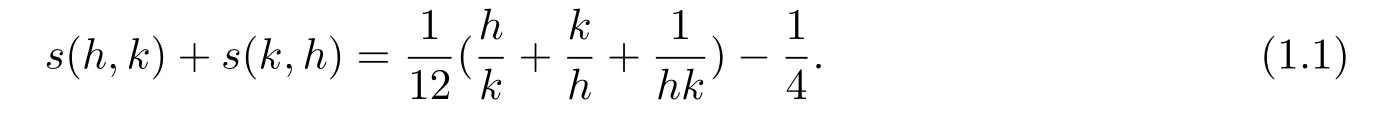
Dedekind[1]基于logη(τ)的变换公式,给出了上式的第一个证明.Rademacher[2],Berndt[3-5]和Dieter[6]都分别给出了这个互反公式的不同证明.
张文鹏等人研究了Dedekind和的混合均值,并得到了较强的渐近公式如下.
命题1.1[7]对于整数q≥3,有
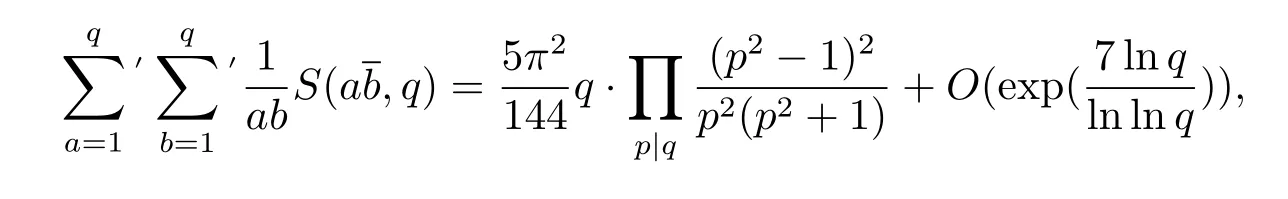
命题1.2[8]设整数n≥1,p为素数,k=pn.则有
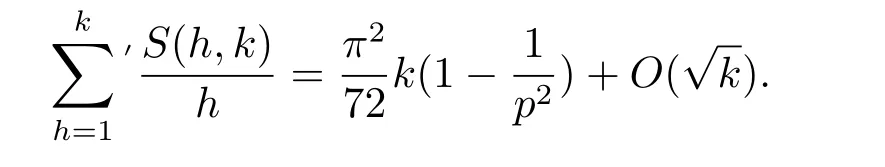
设f为正整数,χ为模f的Dirichlet特征.定义新型Dedekind和如下
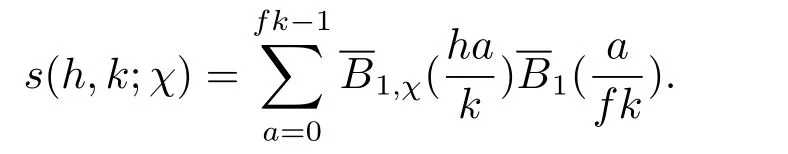
本文将给出s(h,k;χ)的混合均值的渐近公式.主要结论如下.
定理1.1设f为正整数,p>2为素数,满足(f,p)=1.设χ为模f的Dirichlet特征,满足χ(-1)=1.则有
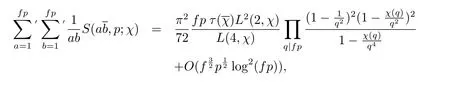
定理 1.2.设f为正整数,p>2为素数,满足(f,p)=1.设χ为模f的Dirichlet特征,满足χ(-1)=1.则有
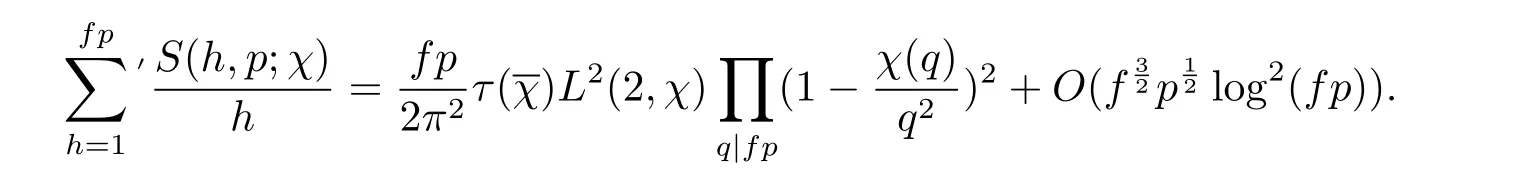
2 一些引理
引理2.1设f,k为正整数,h为任意整数,满足(fk,h)=1与(f,k)=1.设χ为模f的Dirichlet原特征.则有
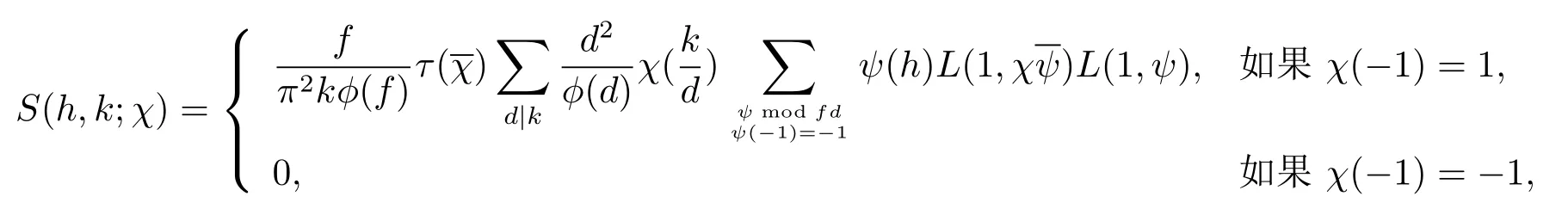
证对任意实数y,由文献[9]中的定理3.1可知
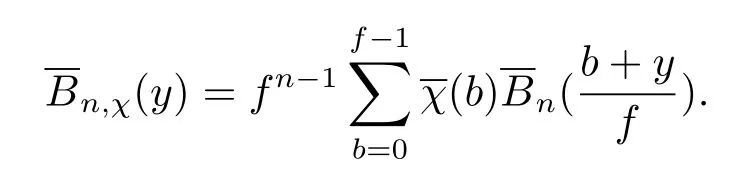
此外当0≤x<1时,有其中e(y)=e2πiy. 因此
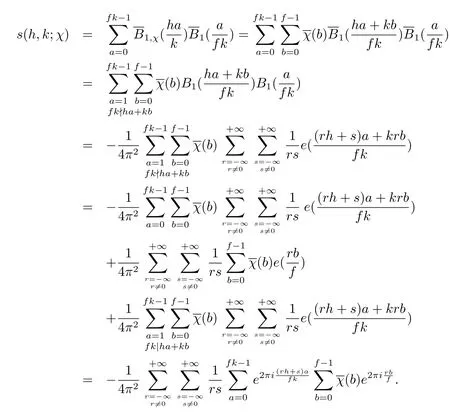
注意到χ为模f的原特征,以及(fk,h)=1,(f,k)=1.可得

再由特征和的正交性质,有

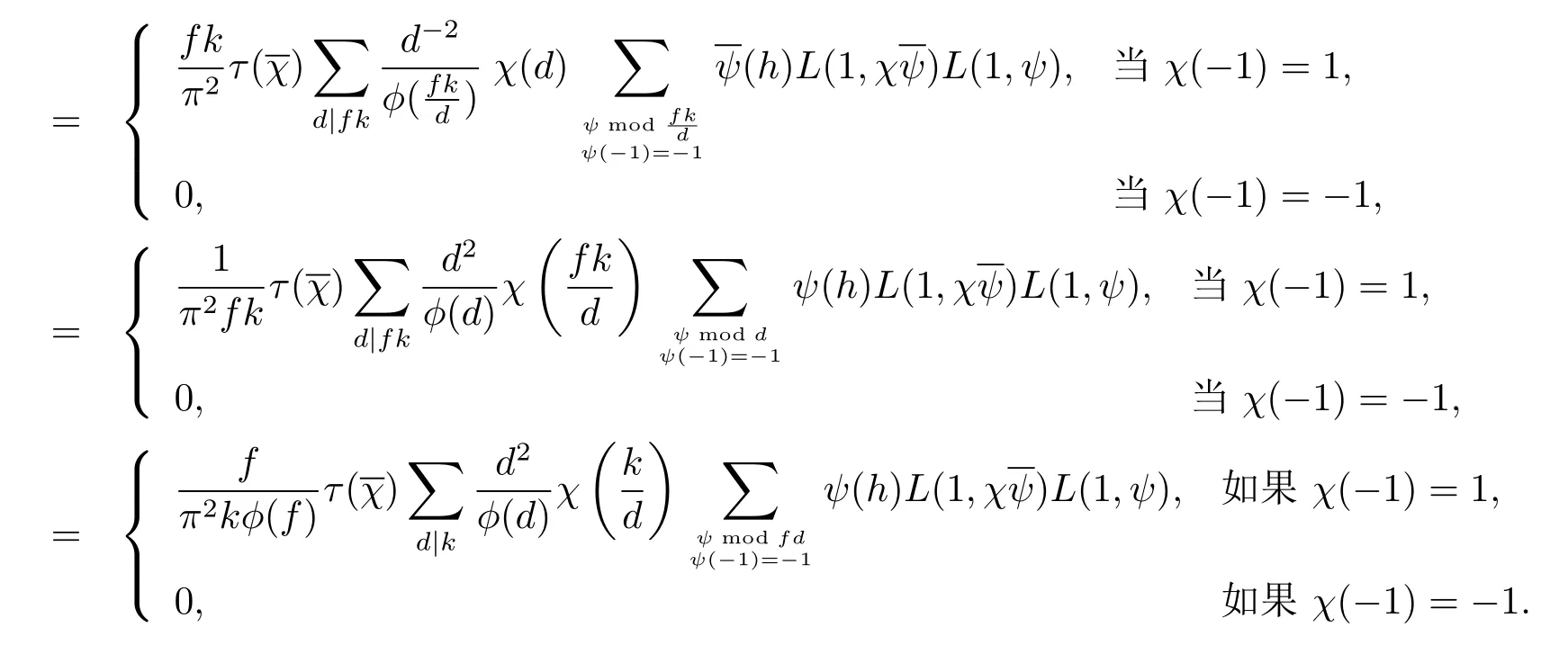
引理2.1证毕.
3 定理1.1的证明

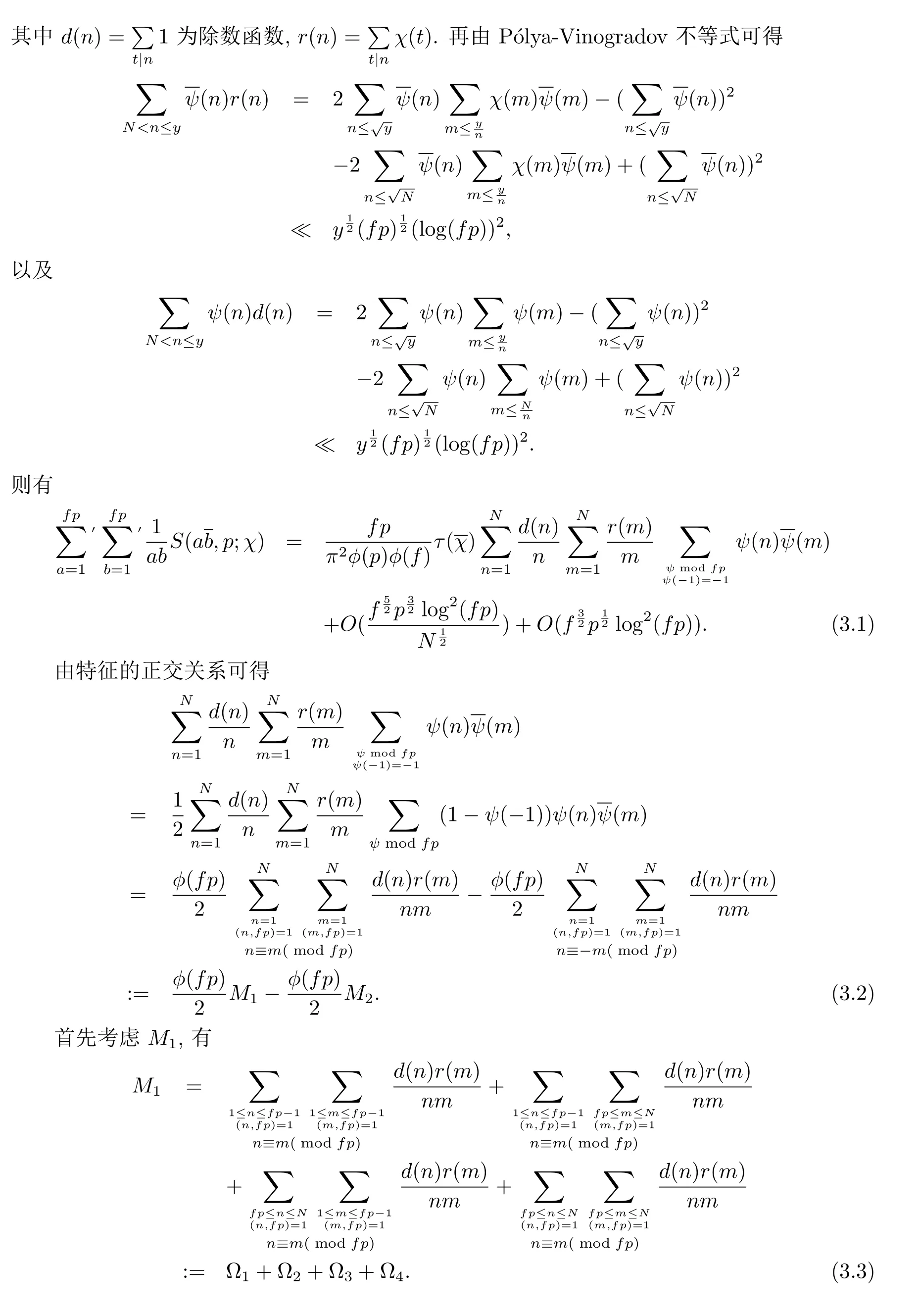


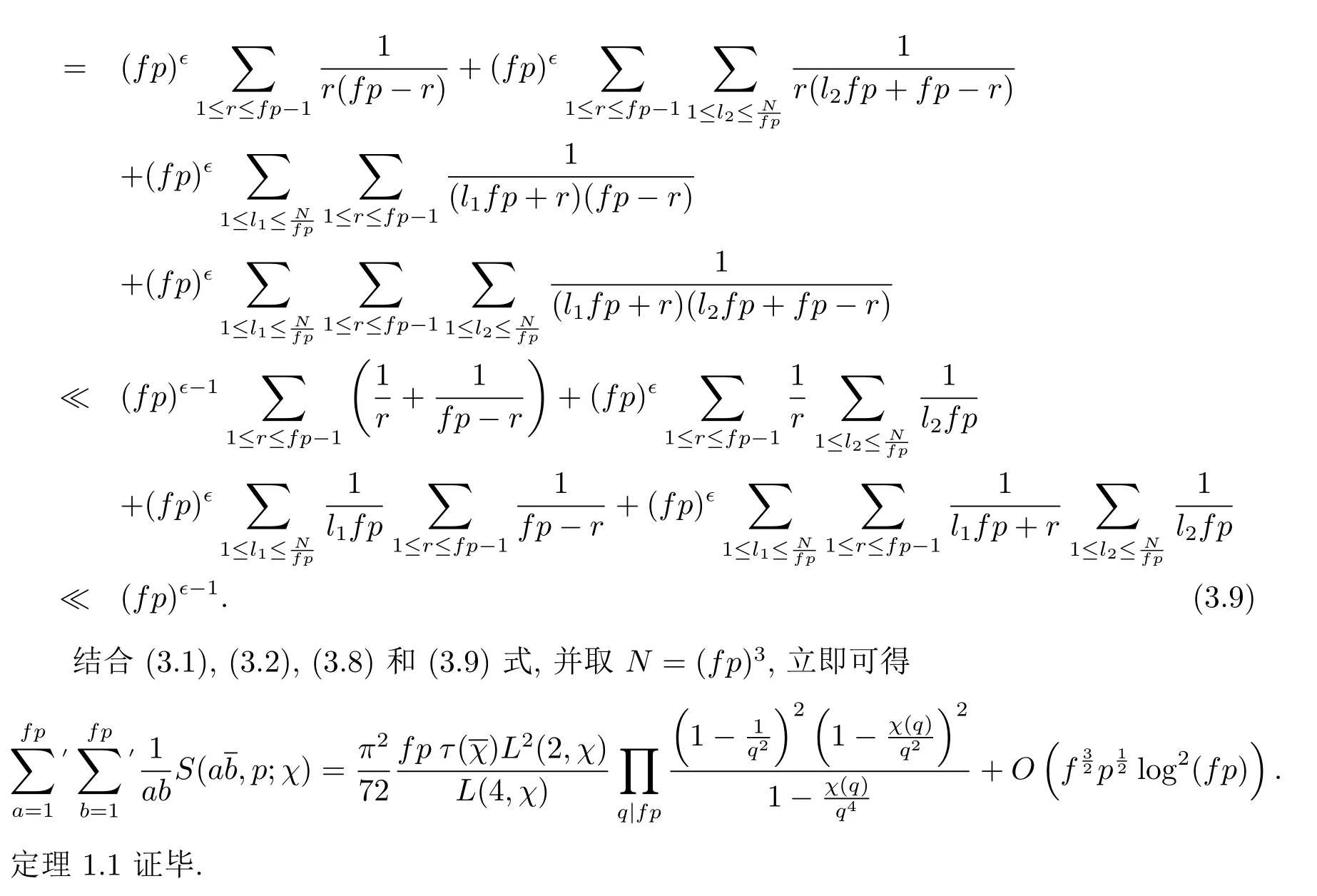
4 定理1.2的证明
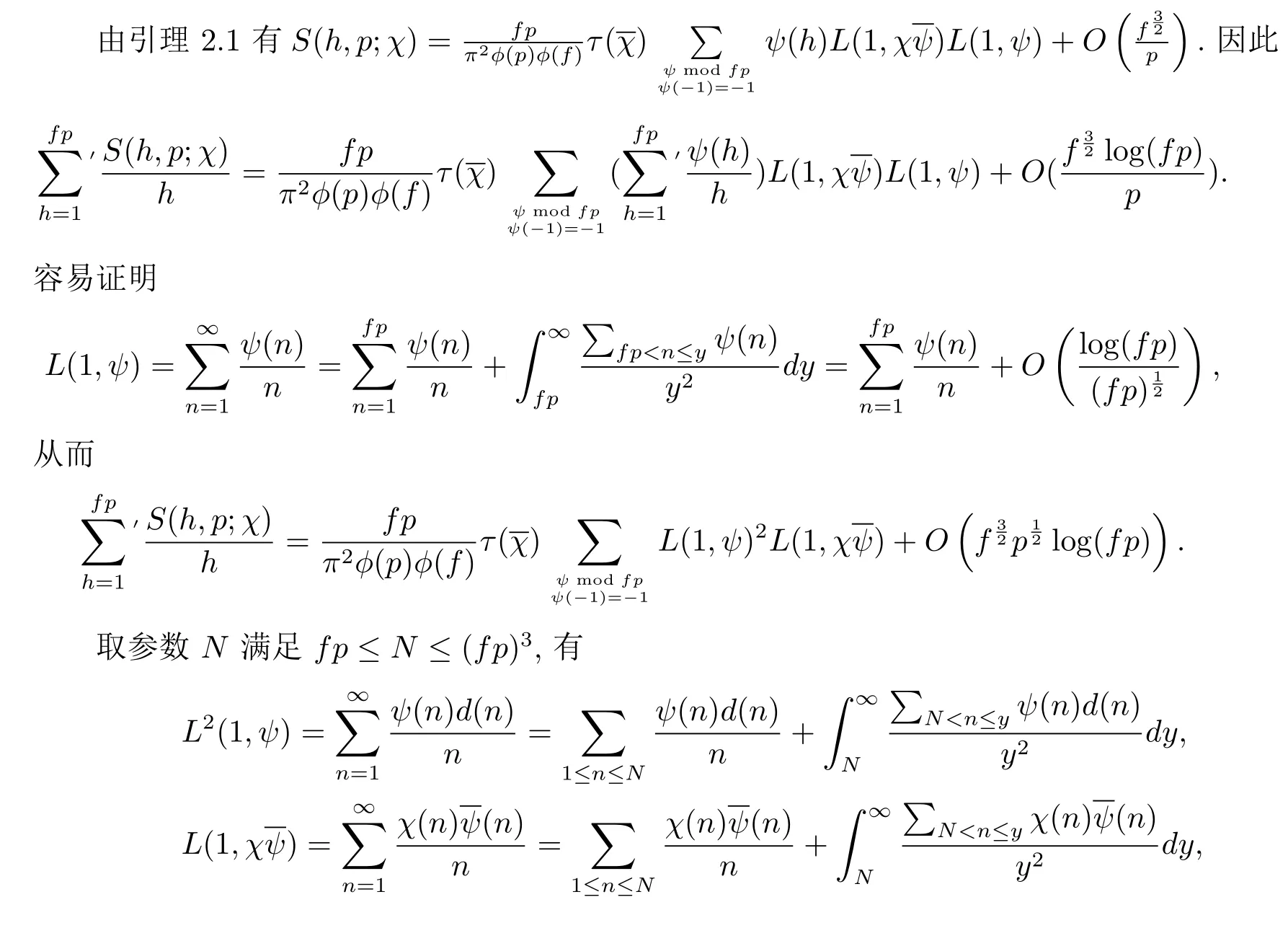


猜你喜欢
杂志排行
数学杂志的其它文章
- HYPOELLIPTIC ESTIMATE FOR SOME COMPLEX VECTOR FIELDS
- FAST AND SLOW DECAY SOLUTIONS FOR SUPERCRITICAL FRACTIONAL ELLIPTIC PROBLEMS IN EXTERIOR DOMAINS
- NORM STRUCTURES OF A FUZZY NORMED SPACE
- MODIFIED LAVRENTIEV REGULARIZATION METHOD FOR THE CAUCHY PROBLEM OFHELMHOLTZ-TYPE EQUATION
- BIFURCATION AND POSITIVE SOLUTIONS OF A p-LAPLACIAN PROBLEM
- 几类区域上不等维的边界唯一性定理
