带固定效应空间误差面板数据模型的经验似然推断
2020-09-21秦永松
周 婷,秦永松
(广西师范大学数学与统计学院,广西桂林 541006)
1 引言
空间计量经济学是在区域经济模型中处理由于空间因素导致的特殊性质的一系列方法[1].空间计量经济学可应用于区域科学、地理经济学、城市经济学等领域,具体来说,如研究区域经济、房屋价值、人均收入等问题.空间面板数据模型是空间计量经济学中经典模型之一,它同时考虑了空间相关性和时间依赖性,将传统的时间序列方法、横截面数据方法以及普通面板数据模型进行综合,学者们对此模型也进行了诸多研究.如Elhorst[2]研究了空间面板数据模型的分类和估计问题;Kapoor等[3]研究了误差项是空间自相关的面板数据模型的参数估计;Yu等[4]研究了带固定效应空间动态面板数据模型的拟极大似然估计(QMLE);Lee和Yu[5]进一步研究了带固定效应的空间自回归面板数据模型的QMLE,并提出正交转换的间接估计方法;文利霞[6]研究了空间误差面板数据模型的拟极大似然估计及其渐近性质;戴晓文等[7]基于工具变量法研究了含有个体固定效应的空间误差面板数据模型参数的分位回归估计,并与均值回归方法做比较,结果表明在处理空间面板数据时工具变量回归估计方法优于均值回归方法;Qin[8]研究了空间误差模型的经验似然估计.由于人为或者客观原因,我们得到的数据不一定是完整的;Wang和Lee[9]研究了数据随机缺失情形下空间面板数据模型的广义矩估计、非线性最小二乘估计和两阶段最小二乘估计估计,并对这三种估计方法得到的结果进行了比较;于力超和金勇进[10]研究了数据缺失机制为非随机缺失情形的面板数据参数估计方法.
对空间计量模型进行估计,使用比较多的估计方法是(拟)极大似然估计法(如文献[4,5,11])、广义矩估计法(如文献[9,13])、两阶段最小二乘法(如文献[9,13])等.空间计量模型的理论和应用研究均比较深入且成熟.经验似然是Owen[14]于1988年在完全样本下提出的一种非参数统计推断方法,其是在一定约束条件下将参数似然比极大化,有类似于Bootstrap的抽样特性.经验似然方法应用广泛,可应用于各种统计模型,学者们对经验似然也进行了诸多研究.Owen[15,16]将经验似然应用到线性回归模型的统计推断;石坚[17]运用经验似然方法修正了线性相关模型中误差方差的传统最小二乘估计,修正后的估计的渐近方差比传统估计的更小;Cui和Chen[18]将经验似然应用到线性变量含误差模型;Kostov[19]研究了空间分位数回归模型的经验似然推断;陈燕红[20]研究了时间序列模型的经验似然推断.据我们所知,目前尚没有研究面板数据空间计量经济模型的文献报导.于是,本文探讨空间面板数据模型的经验似然推断,在正则条件下构造了空间面板数据模型的经验似然统计量,证明了该统计量的极限分布为卡方分布.
2 空间面板数据模型
一般的空间面板数据模型[5]
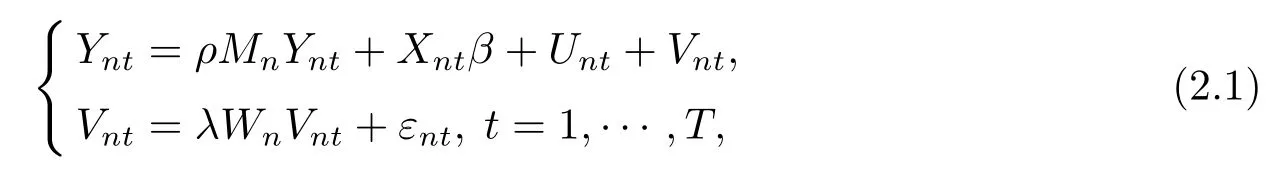
其中Ynt=(y1t,···,ynt)′为n×1维被解释变量;Xnt为n×k维非随机解释变量向量;β为k×1维系数向量.Mn和Wn均为n×n维空间权重矩阵,其中mij为矩阵Mn的(i,j)元素,mii=0;wij为矩阵Wn的(i,j)元素,wii=0.Unt为n×1维固定效应向量.Vnt为自相关误差项.εnt=(ε1t,ε2t,···,εnt)′为n×1 维随机扰动项,其分量的均值为 0,协方差为σ2,且独立同分布.ρ和λ为空间相关系数.在本文中,“′”表示矩阵转置.
由于t=1,···,T,模型(2.1)可改写为[1]
(1)当λ=0时,模型(2.2)即为空间滞后面板数据模型
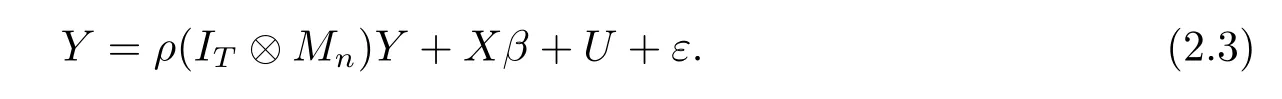
(2)当ρ=0时,模型(2.2)即为空间误差面板数据模型
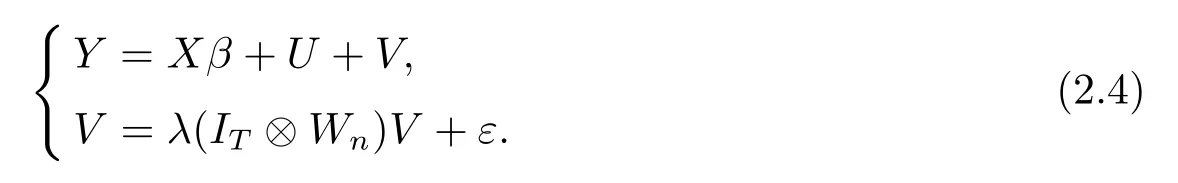
3 空间误差面板数据模型的经验似然估计
为了完整性,我们重述空间误差面板数据模型
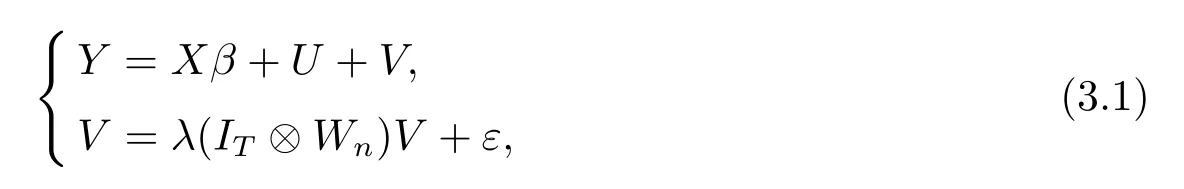
为了描述方便,我们重新记nT×k维解释变量向量
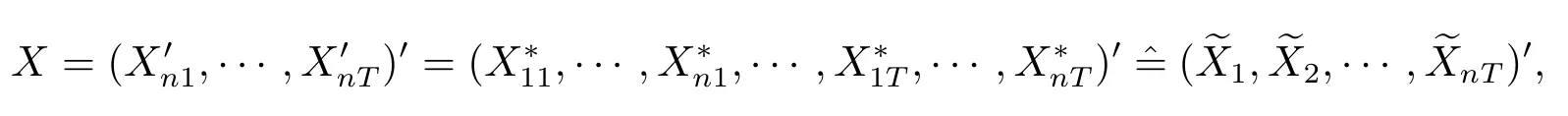
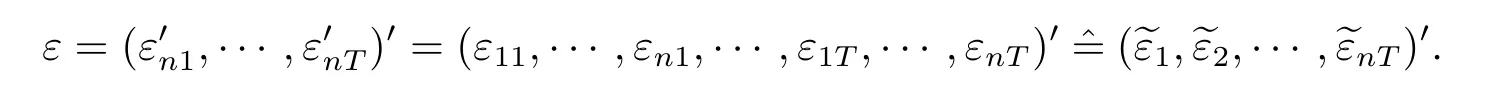
记RnT(λ)=InT-λ(IT⊗Wn),且为nT×nT维向量,为1×nT维向量.假设RnT(λ)可逆,则模型(3.1)可改写为

其中ε=R(λ)(Y-Xβ-U).被解释变量Y的拟对数似然函数
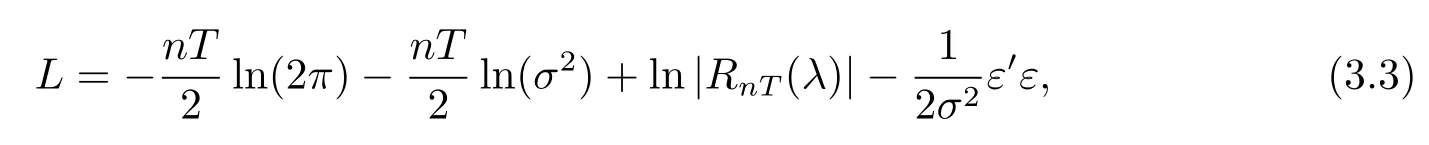
其中ε=RnT(λ)(Y-Xβ-U).
令GnT=(IT⊗Wn)R-1(λ)且均为nT×nT维矩阵,且是对称矩阵.由文献[1]可得
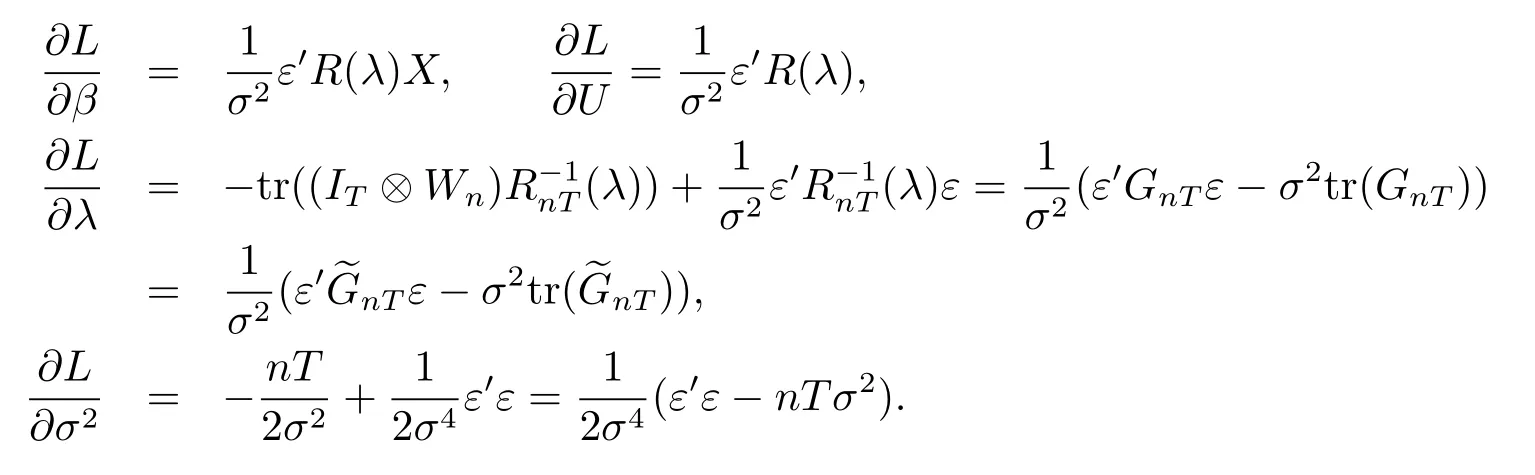
令以上偏导数等于0,我们有以下式子
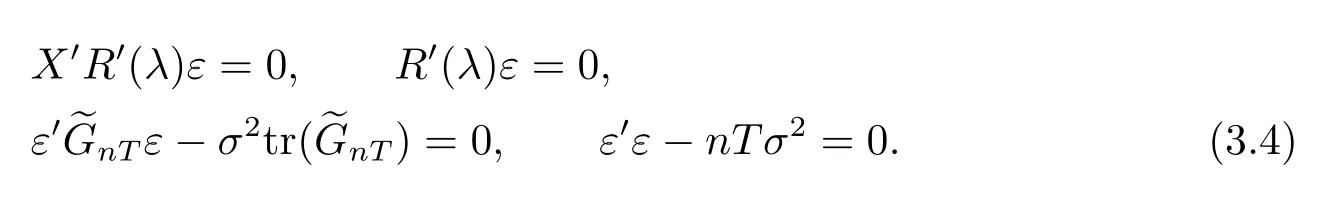
分别用gij和表示矩阵GnT和的(i,j)元素,用bi表示矩阵X′R′(λ)的第i列,用ri表示矩阵R′nT(λ)的第i列.由于X′R′(λ)=(R(λ)X)′,根据X及R(λ)的表达式可知,bi和ri分别为
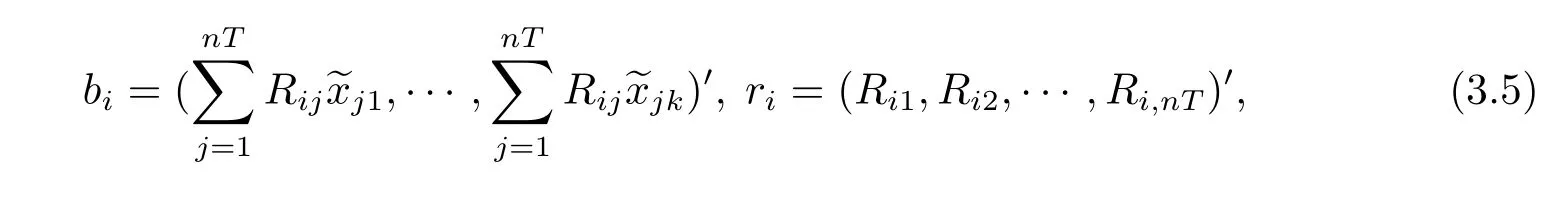
其中i=1,2,···,nT.
我们规定,当求和符号的上标等于0时我们令该和为0.为将(3.4)式的二次型转化为线性形式,引入一个鞅差序列[21].定义σ-域:1≤i≤nT.令
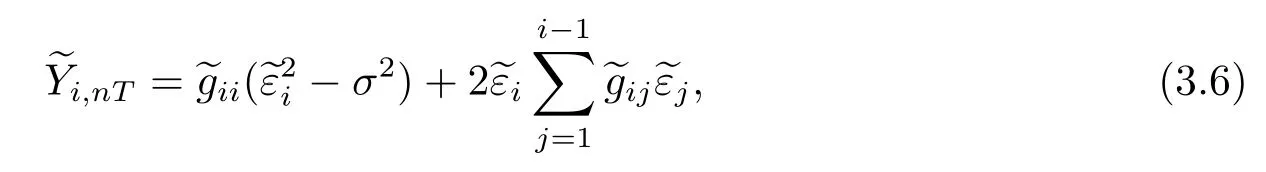
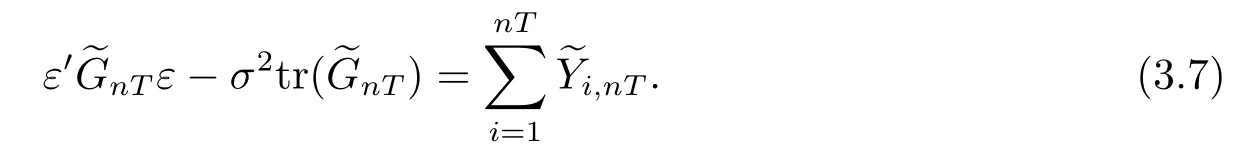
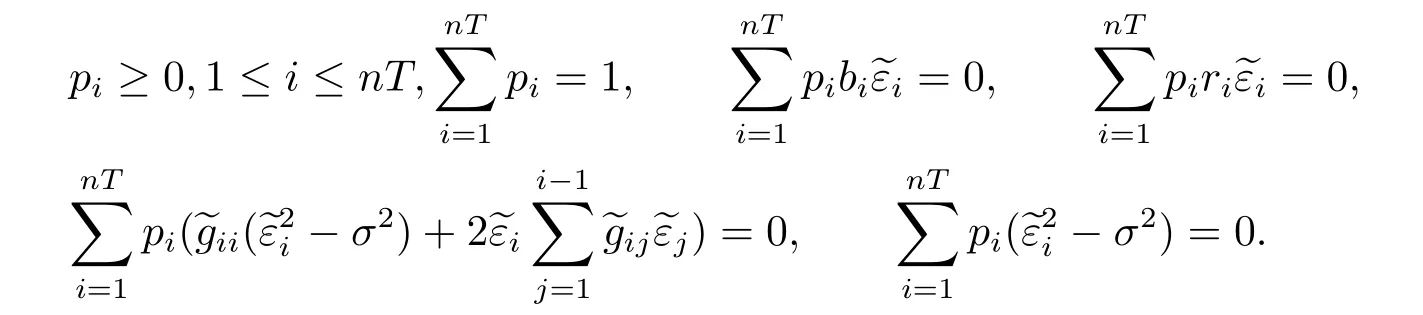
令
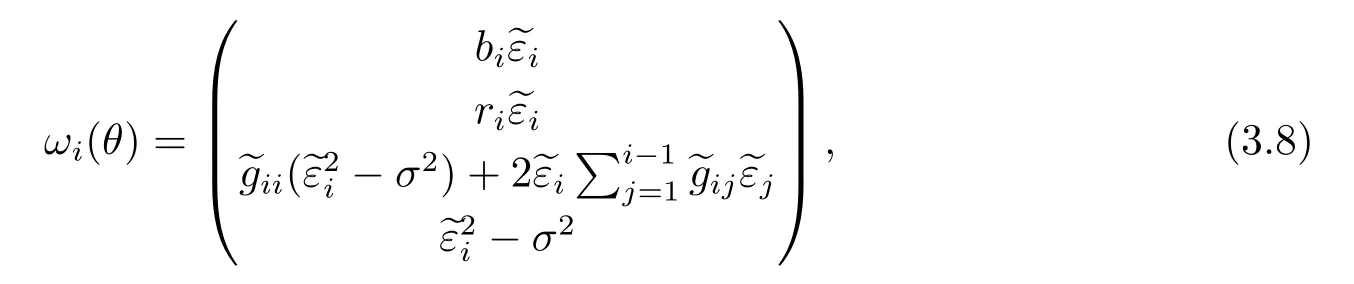
其中ωi(θ)为(k+nT+2)×1维,为ε=RnT(λ)(Y-Xβ-U)的第i部分.由Owen[15],有
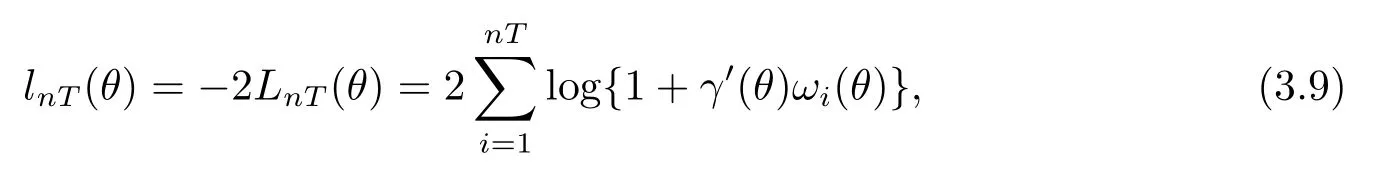
其中γ(θ)∈Rk+nT+2是下面等式的解
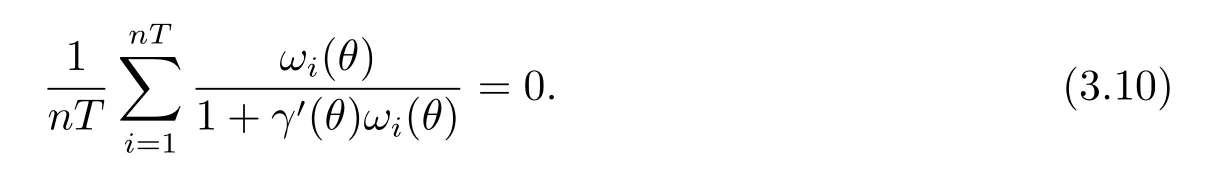
(A1)n为无限大常数,T为有限常数[6].
(A3)RnT(λ)为非奇异矩阵.
(A4)矩阵Wn,RnT(λ)元素的绝对值的行和与列和均一致有界.
(A6)存在常数C1,C2,使其中λmin(A),λmax(A)分别表示矩阵A的最小和最大特征值.Σk+nT+2表示如下
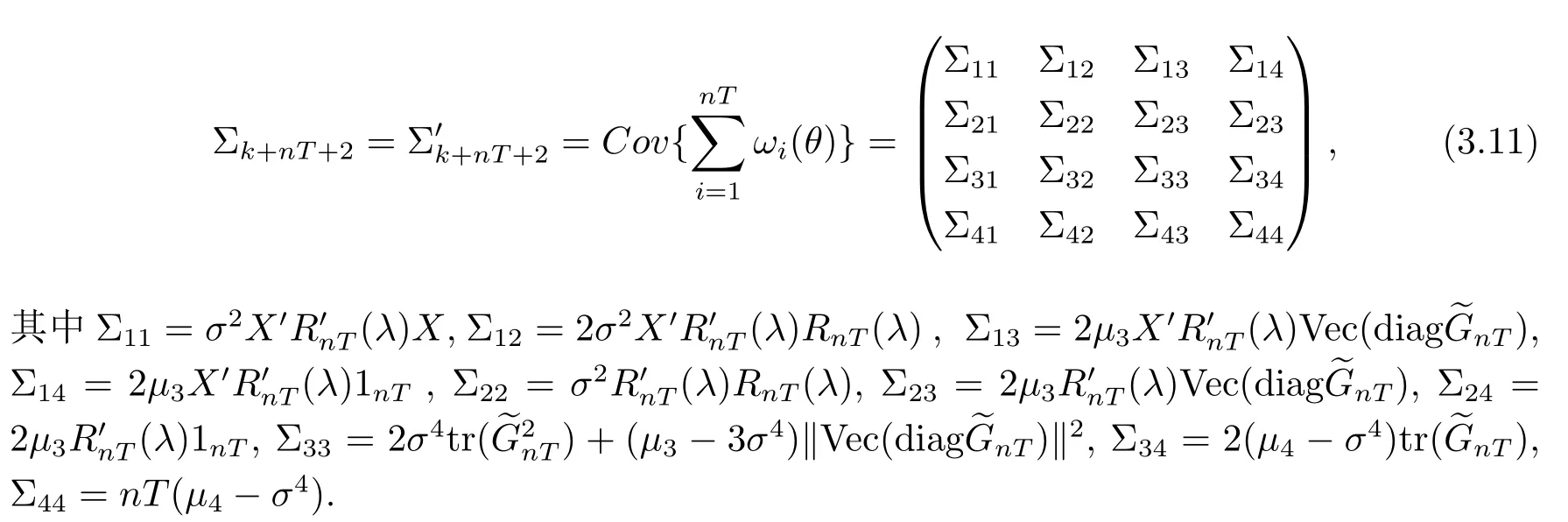
注(A1)源于文献[6],本文考虑n无限而T有限的情形.(A2)和(A3)是空间面板数据模型的常见假设,如Lee和Yu[5],Yu等[4,22].(A3)保证(3.2)的表示方法是有效的.(A4)源于Kelejian和Prucha[21,23],在Lee[13]中也有用到.(A5)和(A6)保证了本文的QnT满足假设条件C2.
引理1[15]令ξ1,···,ξnT是一个平稳随机变量序列,且对常数s>0有E|ξ1|s<∞,那么a.s.
证见文献[15]中引理3的证明.
引理2的准备需要用到文献[21]中的定理1,我们对此定理做以下描述.考虑线性二次型
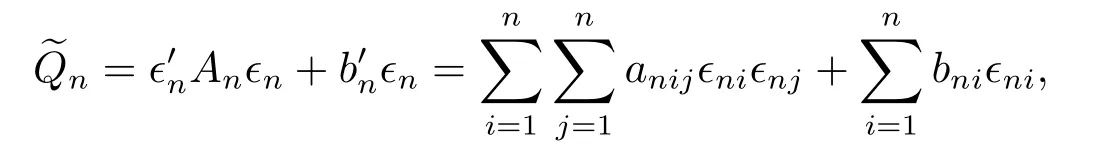
其中∈ni是(实值)随机变量,anij和bni分别代表二次型和线性形式的(实值)系数.需要以下假设.
(C1)实值随机变量序列{∈ni,1≤i≤n,n≥1}满足E(∈ni)=0,且对每一个n≥1随机变量∈n1,···,∈nn完全独立.且存在δ1>0使
(C2)对所有1≤i,j≤n,n≥1有anij=anji,存在δ>0,有2
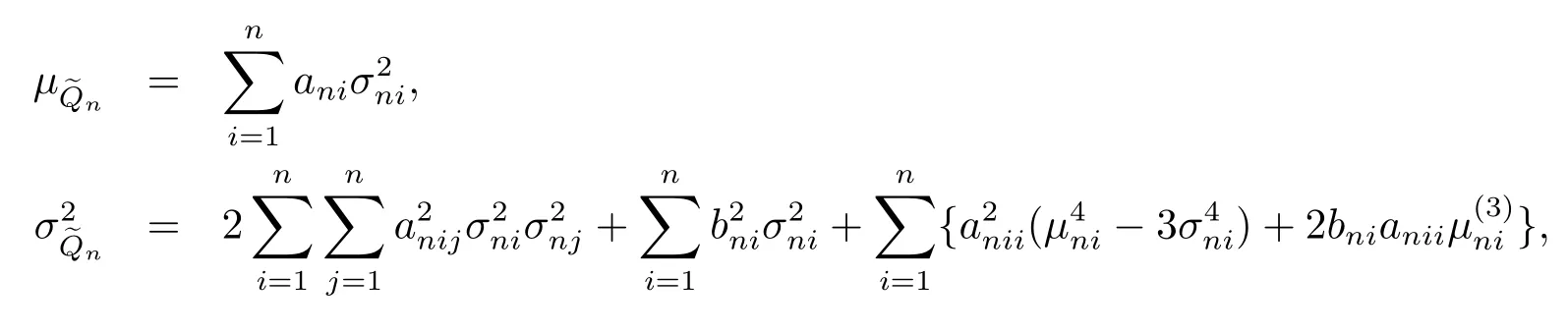
引理2若假设条件(C1)和(C2)成立,且存在常数C>0满足则
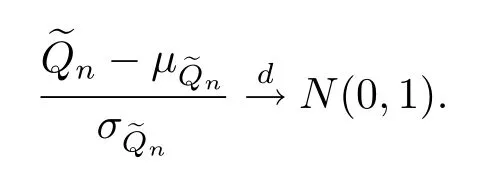
证见文献[21]中的定理1.
引理3若假设条件(A1)–(A6)满足,那么当n→∞时,
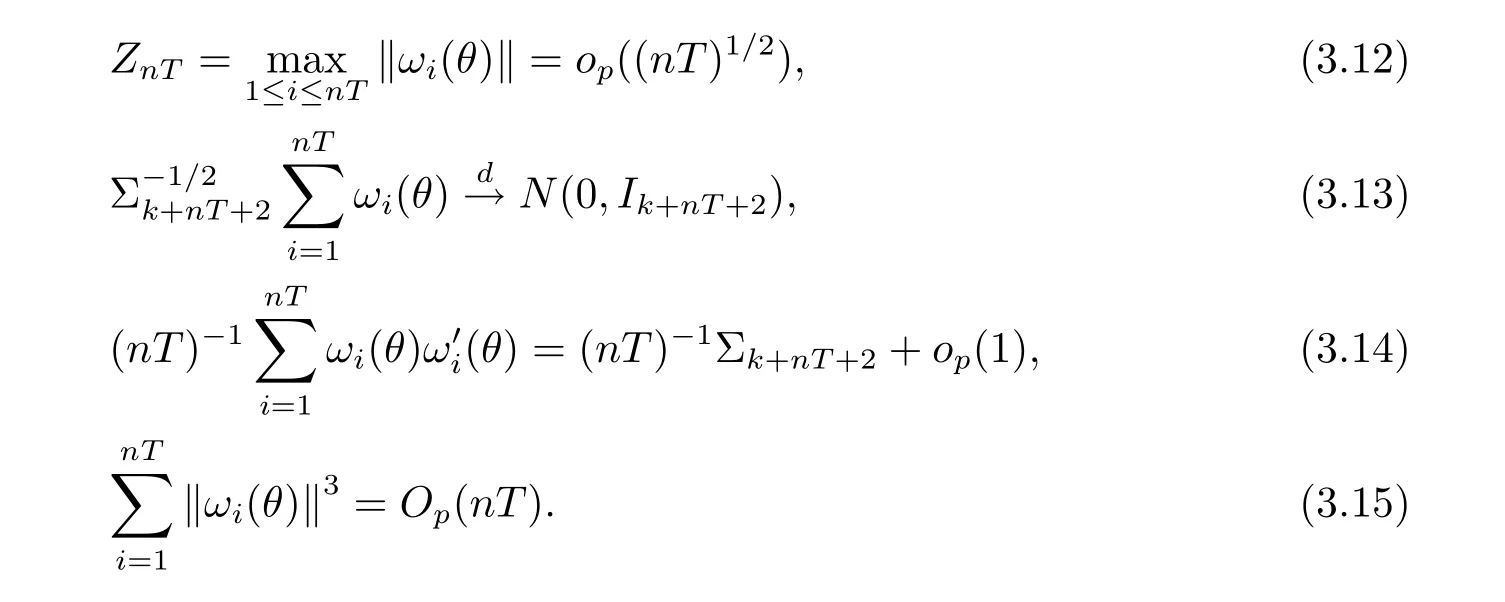
证见第四章.
定理1在(A1)–(A6)假设条件下,当n→∞时,有

证令γ(θ)=γ,ρ0=‖γ‖,γ=ρ0η0.下面证明‖γ‖=Op((nT)-1/2).由 (3.10)式,有
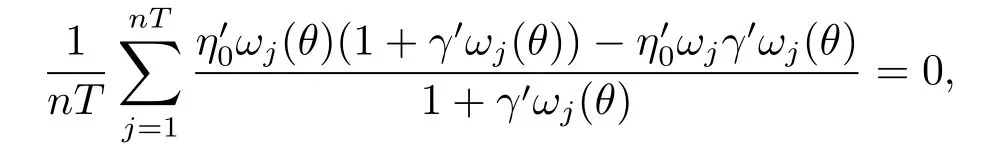
即
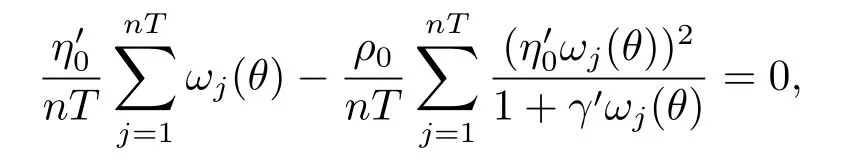
则有
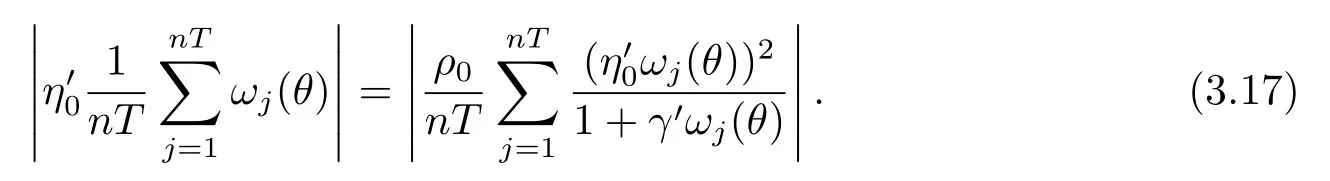



4 引理3的证明
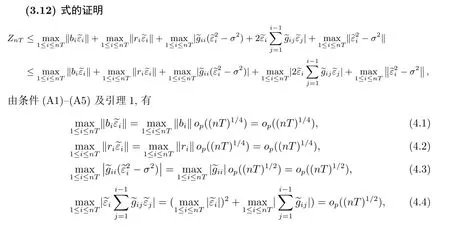




猜你喜欢
杂志排行
数学杂志的其它文章
- HYPOELLIPTIC ESTIMATE FOR SOME COMPLEX VECTOR FIELDS
- FAST AND SLOW DECAY SOLUTIONS FOR SUPERCRITICAL FRACTIONAL ELLIPTIC PROBLEMS IN EXTERIOR DOMAINS
- NORM STRUCTURES OF A FUZZY NORMED SPACE
- MODIFIED LAVRENTIEV REGULARIZATION METHOD FOR THE CAUCHY PROBLEM OFHELMHOLTZ-TYPE EQUATION
- BIFURCATION AND POSITIVE SOLUTIONS OF A p-LAPLACIAN PROBLEM
- 几类区域上不等维的边界唯一性定理
