低矮建筑标模风荷载的主动湍流模拟试验研究
2020-09-21胡尚瑜李秋胜
胡尚瑜, 李秋胜, 张 明
(1. 汕头大学工学院 土木与环境工程系, 广东 汕头 515063; 2. 香港城市大学 建筑学及土木工程学系, 香港 999077; 3. 国电环境保护研究院有限公司 国家环境保护大气物理模拟与污染物控制重点实验室, 南京 210031)
0 引 言
低矮建筑的风洞试验通常需要采用大比例尺(大于1∶100)模型。常规风洞限于风洞截面和边界效应,低频湍流模拟能力缺失,难以满足湍流积分尺度相似性。目前,常规风洞可通过增设主动湍流装置(如振动翼栅[1-2]、振动尖塔阵[3]等)注入低频脉动能量,对风洞大气边界层低频湍流模拟进行改善,或通过设计阵列多风扇风洞[4-7]等主动风洞,改变来流风速,形成突变流场、定常流场或可模拟较大湍流积分尺度的流场。在常规风洞的基础上,爱荷华州立大学Haan等[8]通过设计旁路改变气流流量,产生阵风效应的非平稳或平稳风速流场。佛罗里达国际大学风工程中心结合阵列风扇的主动控制与传统被动模拟技术研发“风墙”装置,模拟大缩尺比例流场[9-10],开展了TTU标模1∶6缩尺模型测压相关试验研究。美国商业与住宅安全保障中心(IBHS)Brown等[11]利用由105个直径1.68 m的小风扇多排阵列组成的大型风洞实验室(工作截面宽44.2 m、高18.3 m、实验段长度为44.2 m)开展了1∶1全尺寸TTU标模测压试验研究,并以实测结果为基准,评估了全尺寸风洞模拟试验结果的适用性和准确性。西安大略大学Hangan等[12]研制了边界层和龙卷风混合多功能流场模拟风洞,开展了全尺寸低矮建筑模型风洞试验研究。
虽然低矮建筑全尺寸或大缩尺比例模型风洞试验研究[13]可以减小由缩尺模型比例引起的雷诺数效应,但低频湍流缺失问题更为突出。因此,有必要对湍流积分尺度和低频湍流对低矮建筑风压分布规律的影响机制进行研究。本文采用主动与被动湍流相结合的方法,在阵风风洞中模拟不同湍流积分尺度和湍流强度的流场,开展1∶50低矮建筑标准模型测压试验研究,比较分析顺风向湍流积分尺度与湍流强度对屋面气流分离再附区域和锥形涡作用下的角部边缘区域的平均风压、脉动风压和峰值负压产生的影响程度,并以现场实测结果[14-17]为基准,评估阵风风洞模拟低矮建筑标准模型测压试验结果的适用性。
1 风洞试验研究
1.1 阵风风洞简介
本文风洞试验在国家环境保护大气物理与污染控制重点实验室的阵风风洞中开展。该风洞试验段工作截面宽2.5 m、高2 m,边界层长度为20 m,常规最大风速可达50 m/s,主动阵风模拟最大风速为30 m/s。如图1所示,主动阵风风洞在动力段下游与整流段之间布置了一个旁路段。当分流门关闭时,主动阵风风洞可视作常规、定常流速风洞;当旁路开启时,主通道气流被部分分流到旁路,使主通道中的气流速度发生快速变化,可产生阵风效应,实现阵风因子在1.1~1.6之间的周期波形的阵风,可视作阵风风洞。本次试验采用常规被动湍流模拟与主动阵风模拟相结合的方式,可实现对大气边界层中不同湍流积分尺度流场的模拟。
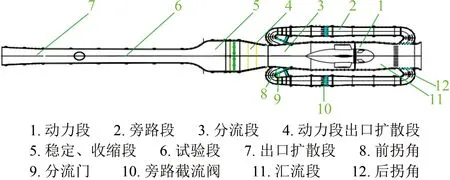
图1 主动阵风风洞结构简图
1.2 近地风场模拟
试验模拟的流场工况分为两大类:常规边界层风场和阵风边界层风场。常规边界层风场采用尖塔和粗糙元等被动湍流模拟装置进行模拟生成。相关模拟的常规边界层风场为CBL-1和CBL-2工况。阵风边界层风场(CBL-1 and Active Gust)是在常规边界层风场CBL-1的基础上,通过旁路主动控制装置向流场中注入低频湍流,以达到在不显著改变流场湍流强度的前提下增大湍流积分尺度的目的。本文平均风速剖面以对应现场实测10 m标准高度的平均风速uref作为参考,对各高度的平均风速进行归一化。图2给出了常规边界层风场(2种工况)、阵风边界层风场和TTU现场实测风场的平均风速剖面的对比结果。可以看出,3种工况下的风速剖面均与实测风速剖面非常吻合,表明增加低频湍流分量对来流平均风速剖面影响甚微。
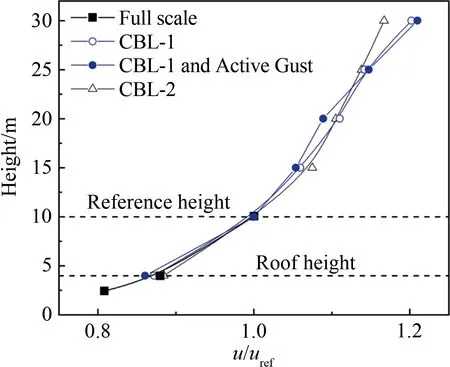
图2 平均风速剖面
图3给出了常规边界层风场、阵风边界层风场和TTU现场实测风场的顺风向、横风向和竖风向湍流剖面的对比结果。阵风边界层风场的顺风向湍流强度Iu略大于相应的常规边界层风场的顺风向湍流强度;而阵风边界层风场的横风向湍流强度Iv和竖风向湍流强度Iw则与常规边界层风场的结果非常接近。CBL-1和CBL-1 and Active Gust工况下的顺风向和横风向湍流强度略小于现场实测值,竖风向湍流强度大于实测值。
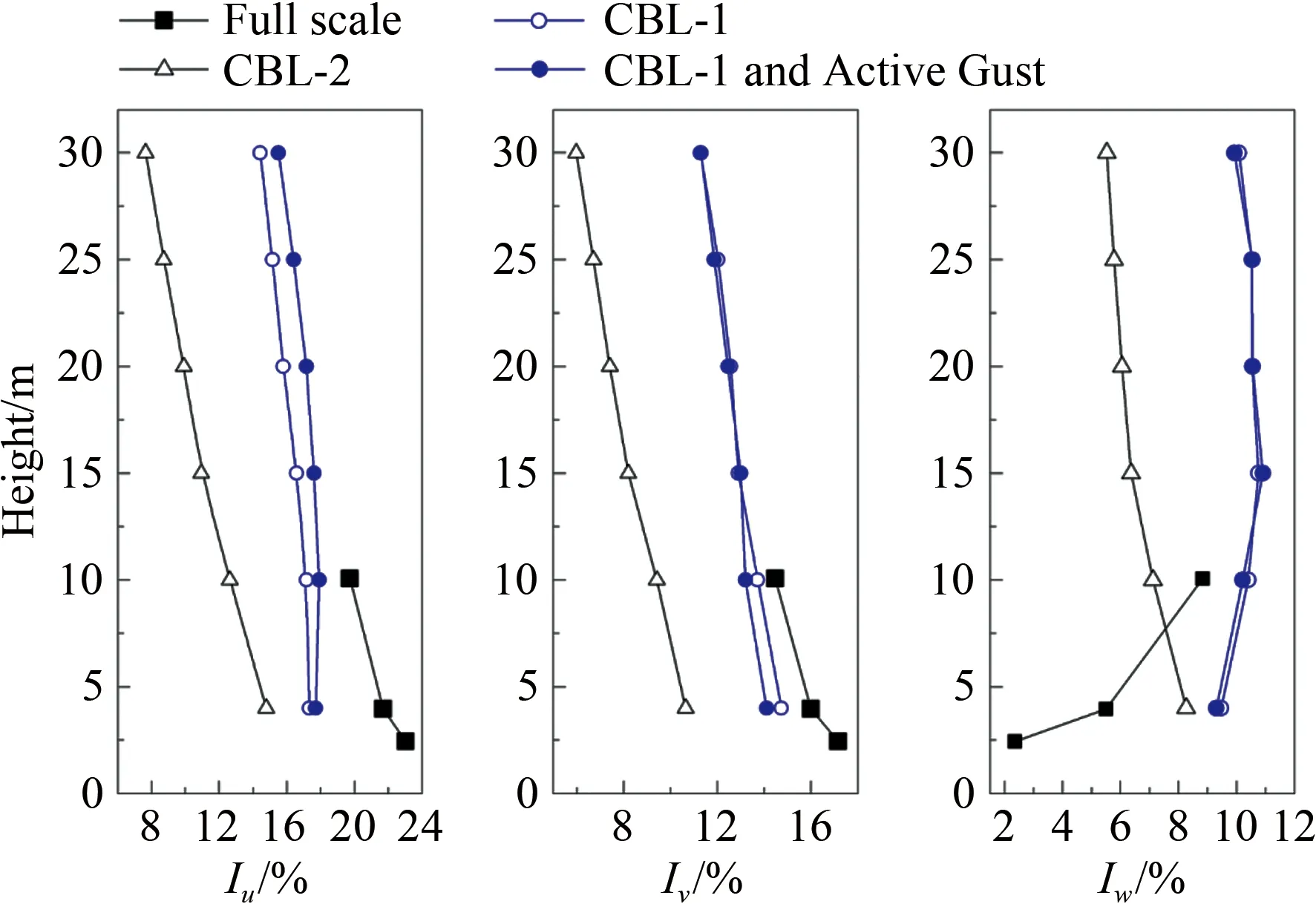
图3 平均湍流剖面
表1列出了10 m参考高度和3.950 m平均屋面高度处(即平坡屋顶高度3.988 m与屋檐高度3.912 m的平均值)各工况的湍流强度、湍流积分尺度模拟统计值。CBL-1工况下,平均屋面高度顺风向湍流强度Iu、横风向湍流强度Iv和竖风向湍流强度Iw的均值分别为17.3%、14.7%和9.5%,Iv/Iu、Iw/Iu分别为0.85、0.55;CBL-2工况下,3个方向的湍流强度均值分别为14.8%、10.7%和8.3%,Iv/Iu、Iw/Iu分别为0.72、0.56;而实测平均屋面高度的Iv/Iu、Iw/Iu分别为0.74、0.25。CBL-1和CBL-2工况下的湍流强度比值Iv/Iu差别显著。
同时,由表1可知:在10 m参考高度处,CBL-1and Active Gust工况下的顺风向湍流积分尺度Lu最大可达81.5 m,约为CBL-1工况(31.0 m)的2.63倍;在3.950 m平均屋面高度处,CBL-1 and Active Gust工况下的Lu最大可达52.0 m,约为CBL-1工况(27.5 m)的1.89倍,顺风向湍流积分尺度Lu增加显著。而常规边界层风场与阵风边界层风场的横风向湍流积分尺度Lv和竖风向湍流积分尺度Lw差别很小,且均与实测结果[17]差距较大。
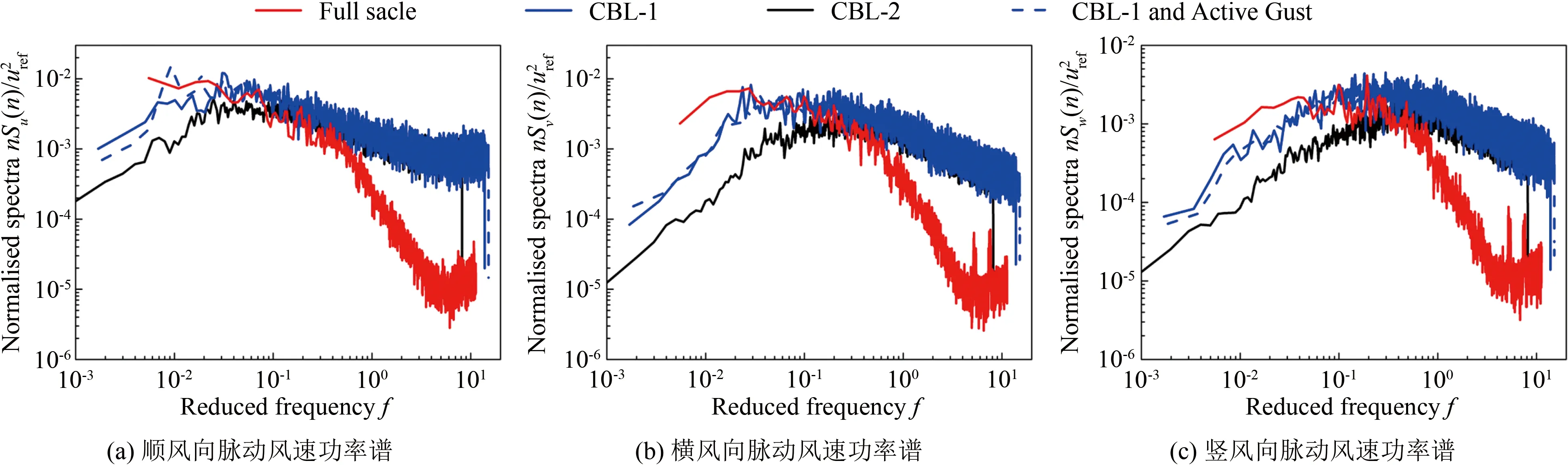
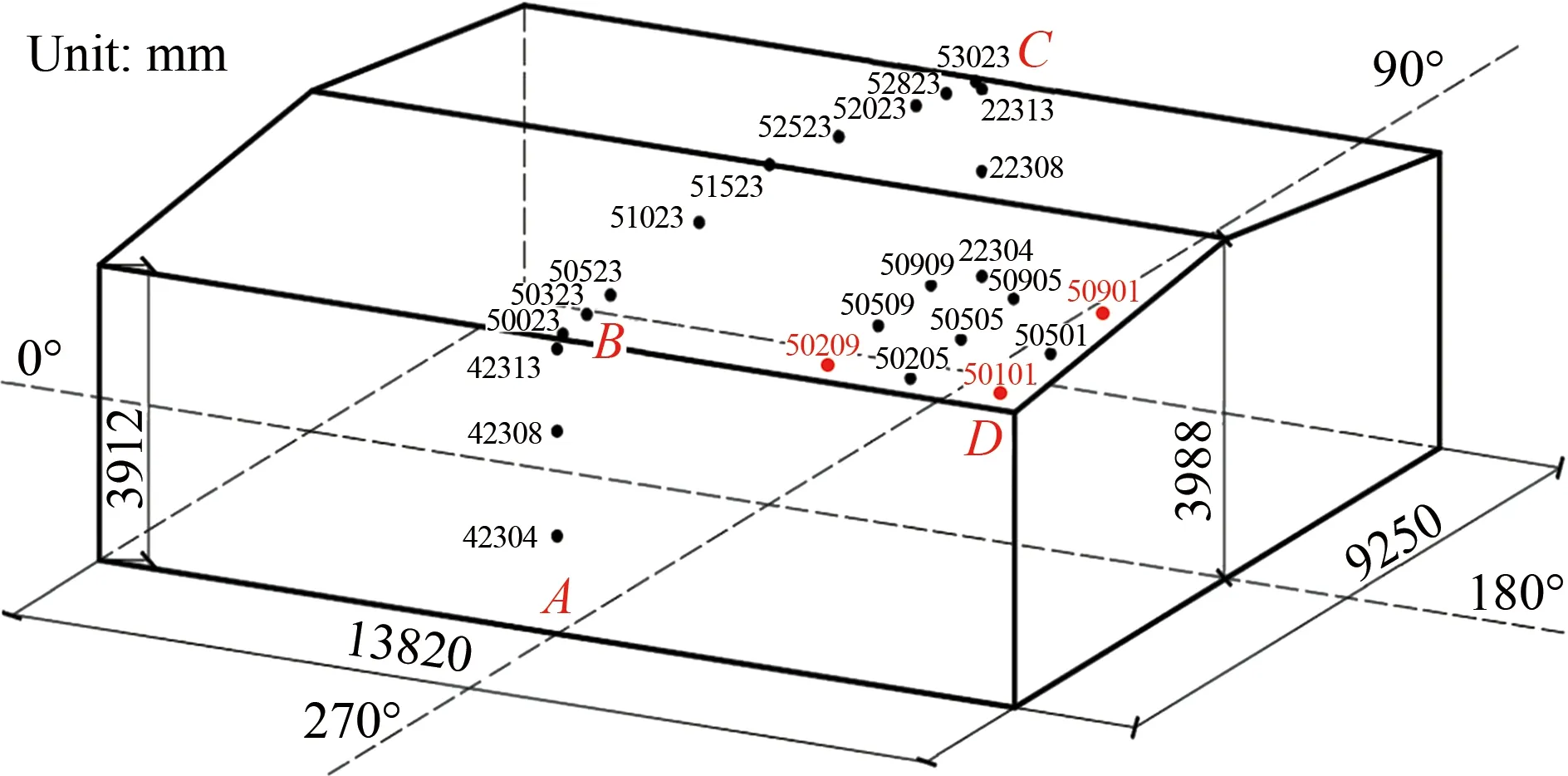
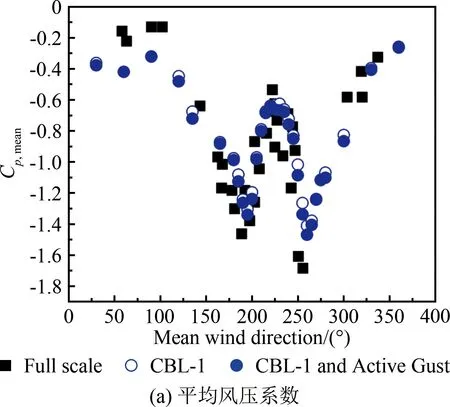
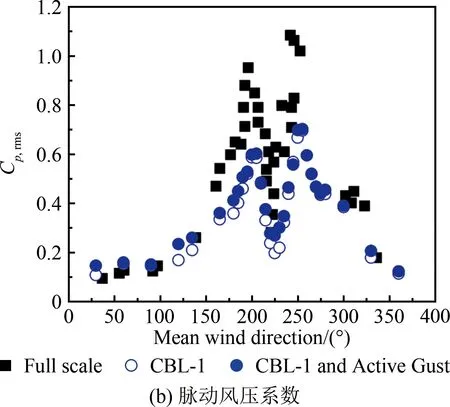
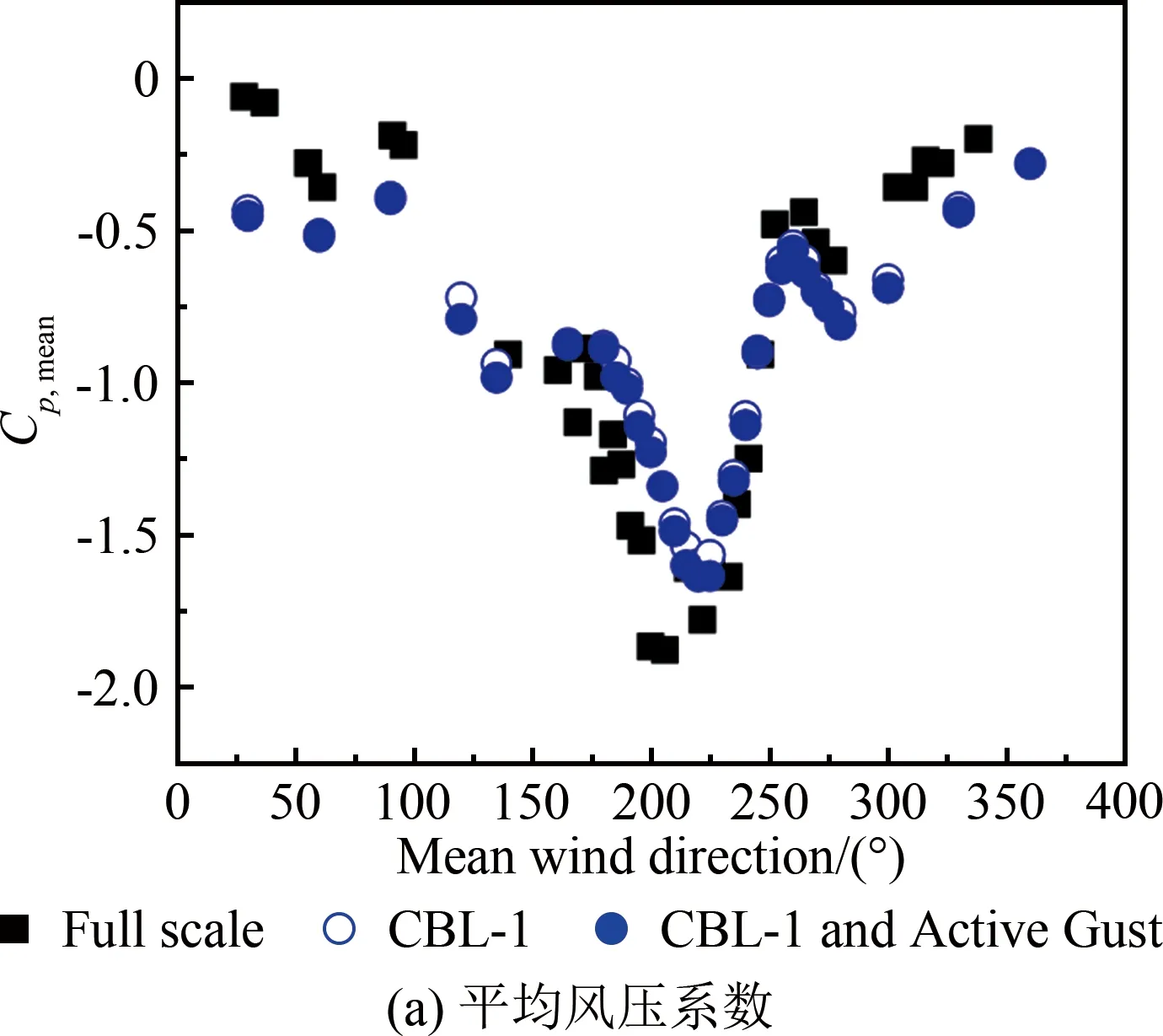
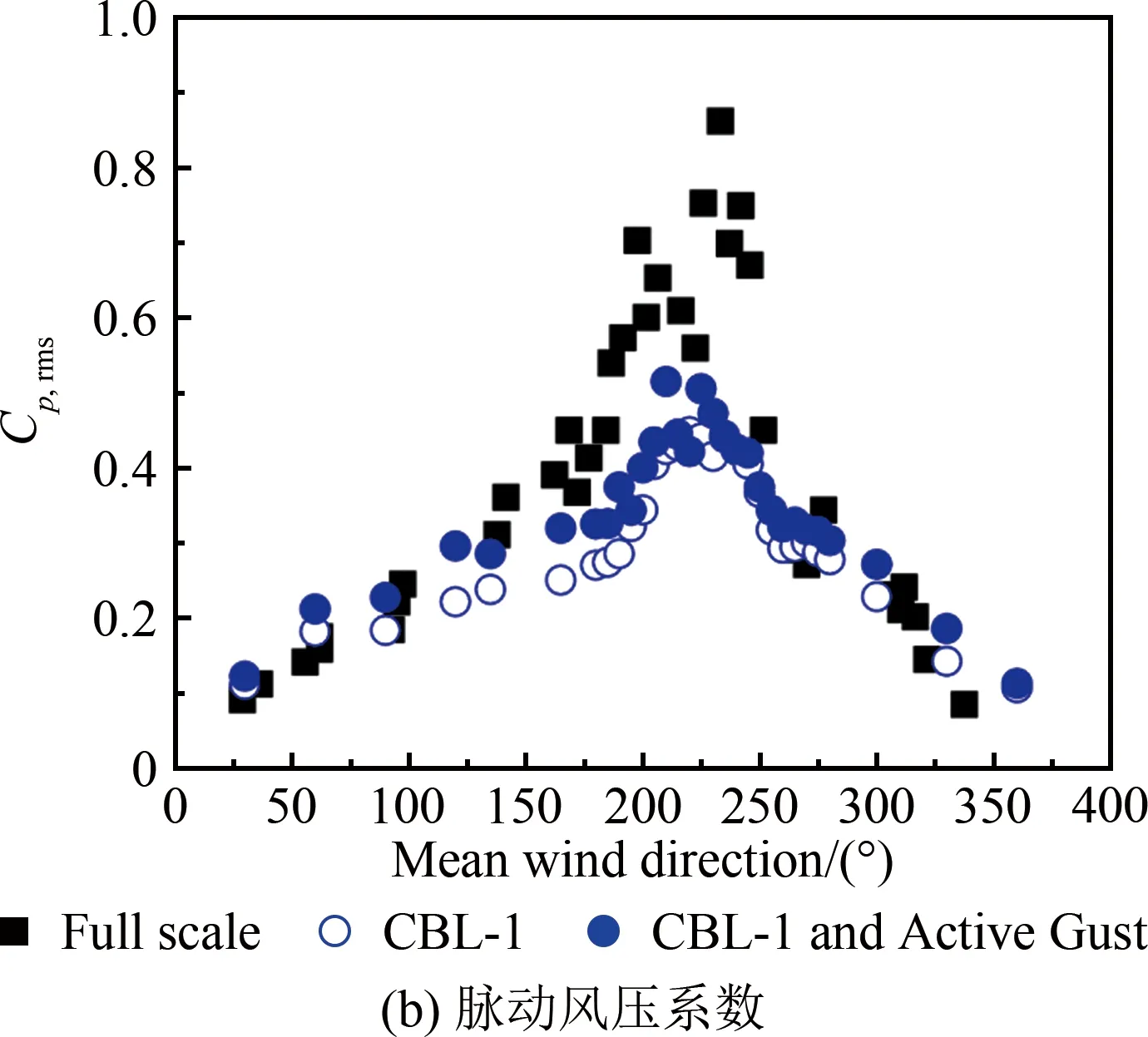
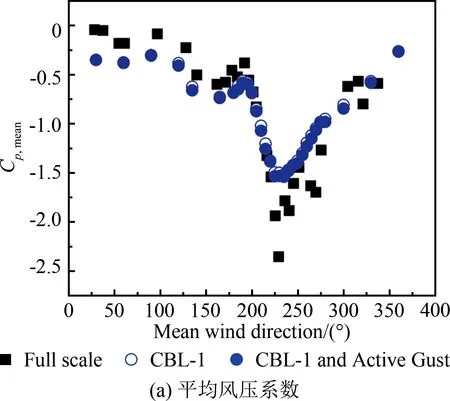
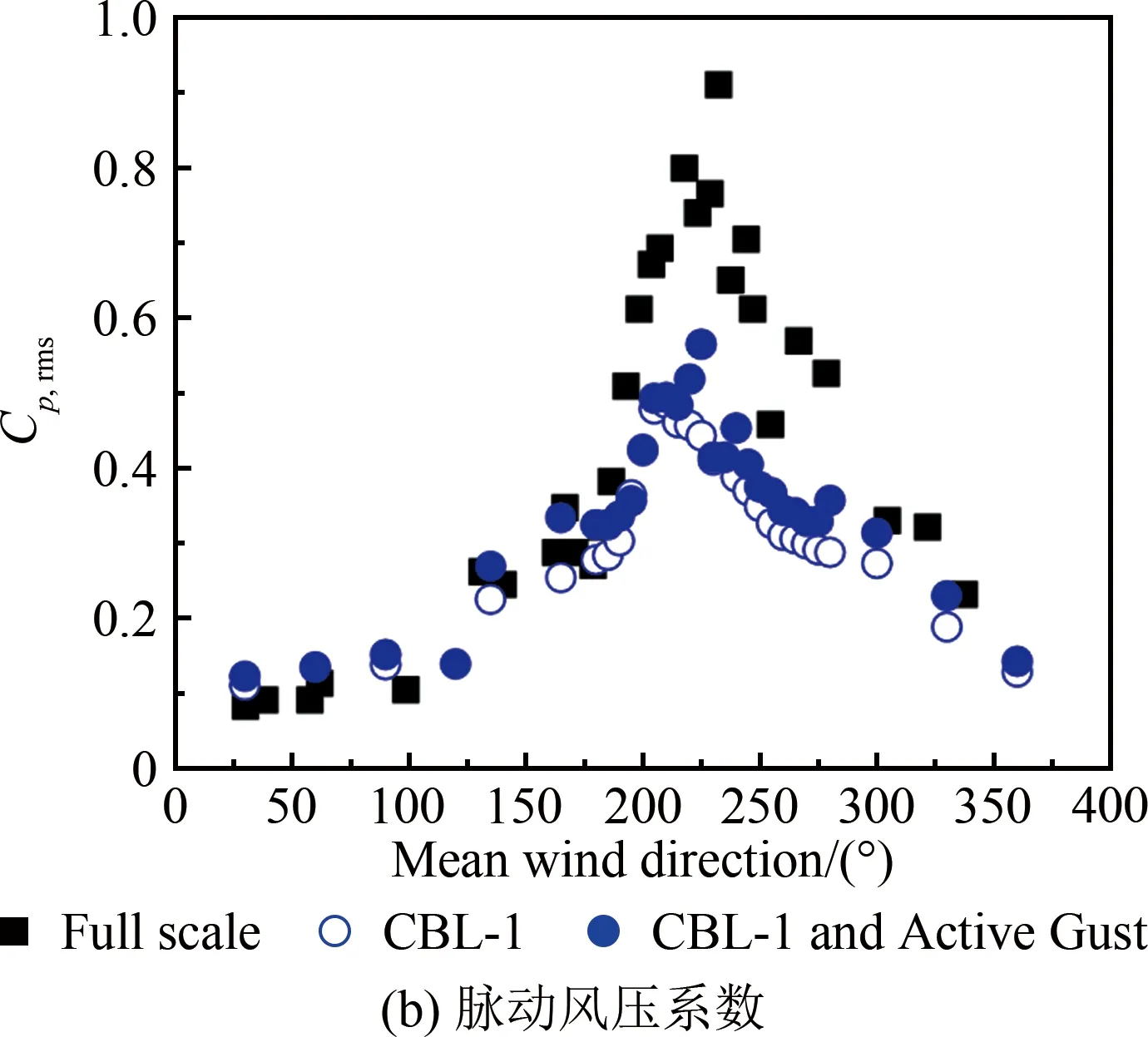
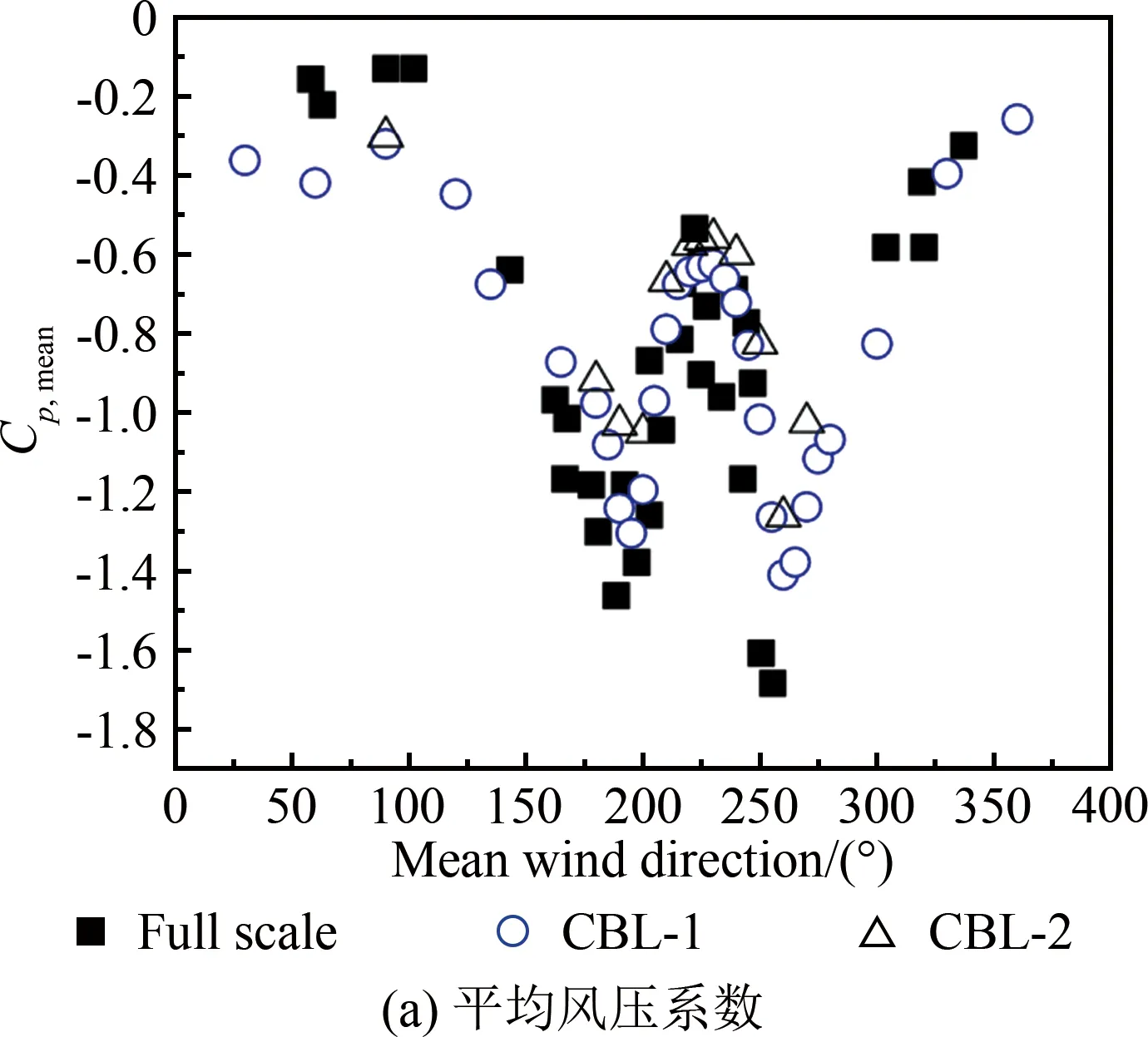
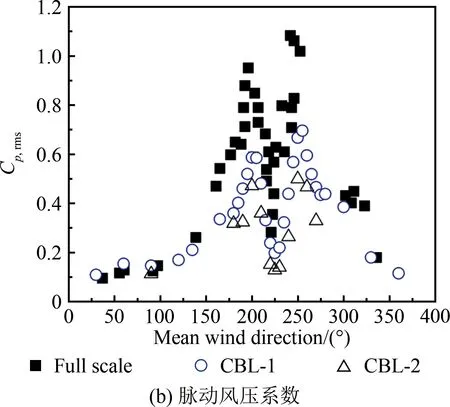
图4给出了不同湍流尺度下平均屋面高度处的顺风向、横风向及竖风向脉动风速功率谱对比(横轴为折减频率f=nz/uz,n为频率,z为高度)。从图中可见:在6×10-3 表1 主动阵风风洞风场参数试验值和现场实测值 图4 平均屋面高度处的脉动风速功率谱 TTU原型实测屋尺寸为13.820 m×9.250 m×3.988 m,试验采用1∶50缩尺模型,截面堵塞度0.4%,其影响可以忽略。如图5所示,风洞试验模型的测点布置及风向角定义与现场实测一致[16-17],平行屋脊方向的风向角定义为0°,按逆时针方向增加;A-B为中轴迎风墙面区域,B-C为中轴屋面区域,C-D为中轴背风墙面区域。 图5 TTU原型实测屋屋面测点布置及风向角定义 风压系数定义为来流风在建筑模型表面引起的实际压力与平坡屋顶和屋檐平均高度处未受扰动的风速压力的比值,计算公式如下: (1) 式中:Cpi(t)和pi(t)分别为第i个测点的风压系数和风压值;p∞为参考高度的静压;uH为平坡屋顶与屋檐平均高度处(3.950 m)未受扰动的平均风速。 风压测量采用美国PSI公司的PSI8400-ESP电子压力扫描系统,试验参考风速测量采用澳大利亚TFI公司的Cobra探针。测压模型采用PVC板制作,满足刚性模型的要求。测压管路长400 mm,内径1 mm,采样频率331 Hz,采样时间300 s。风洞试验参考高度风速约15 m/s,现场实测平均风速范围为8~15 m/s,风速比约为1∶1。时间比约为1∶50,则风洞试验模型采样时间18 s对应实测时间15 min。在处理试验风压数据时,可将采集的总样本300 s风压时程划分为16个18 s时距的子样本。各测点的平均风压系数和脉动风压系数为16个子样本的均值。峰值负压系数定义为:选取各子区间的最小风压系数为观察极值样本,将其组成一个分析样本序列,运用广义极值I分布模型,计算其在超越概率为78%的条件下的极值,即为峰值负压系数。 在来流垂直于屋脊(270°)工况下,屋面中轴线上的平均风压系数Cp,mean、脉动风压系数Cp,rms和峰值负压系数Cp=78%,extreme与来流湍流积分尺度的相关性如图6所示。由图6(a)可知,工况CBL-1与CBL-1 and Active Gust的屋面平均风压系数差别较小,表明湍流积分尺度对屋面中部区域的平均风压系数影响较小。由图6(b)可知,脉动风压系数分布与湍流积分尺度具有较好的正相关性,在CBL-1 and Active Gust工况下,迎风屋面屋檐边缘区域和背风屋面屋檐边缘区域的脉动风压系数均大于CBL-1工况的试验值(迎风屋面屋檐区域脉动风压系数比CBL-1工况增大12.6%)。由图6(c)可知,湍流积分尺度对峰值负压系数(绝对值)的影响规律与脉动风压系数具有类似的趋势和结果,湍流积分尺度与峰值负压系数(绝对值)正相关,例如,在迎风屋面屋檐区域,CBL-1工况下的峰值负压系数试验值为-3.56,CBL-1 and Active Gust工况下为-3.75,增大了约5.3%。同时,由于试验工况的湍流强度与湍流积分尺度均小于实测,因此,实测的屋面中轴线峰值负压系数绝对值均大于试验值,但CBL-1 and Active Gust工况的脉动风压系数、峰值负压系数与实测值更为接近,间接验证了顺风向湍流积分尺度的模拟失真对试验结果有一定的影响。 图6 湍流积分尺度对270°平均风向角屋面中轴线区域风压系数的影响 在来流垂直于屋脊(270°)工况下,2个被动工况CBL-1和CBL-2的屋面中轴线风压系数结果如图7所示:湍流强度对迎风屋檐边缘区域的平均风压系数影响显著。湍流强度与屋面中轴线区域的各风压系数绝对值分布规律具有良好的正相关性。在湍流强度影响下,中轴线迎风屋檐边缘区域平均风压系数变化较大,工况CBL-1较CBL-2增大约17.1%;在迎风屋面屋檐区域,工况CBL-1的脉动风压系数比CBL-2工况增大约17.7%;而峰值负压系数受影响最为显著,如在迎风屋面屋檐区域,CBL-1工况的峰值负压系数试验值为-3.43,CBL-2工况为-2.80,前者比后者(绝对值)增大约22.5%。 为研究湍流积分尺度对屋面角部边缘区域风压的影响,选取图5中的角部代表性测点50101、50901和50209的风洞试验值与文献[16]选取的实测值进行对比分析。测点风压系数与平均风向角的关系如图8~10所示。从图8(a)、9(a)和10(a)可知:在平均风向角180°~270°范围内的斜向风工况下,对于角部边缘区域测点的平均风压系数,工况CBL-1与CBL-1 and Active Gust的结果相差较小,表明湍流积分尺度对锥形涡影响下的角部边缘区域平均风压影响不显著。从图8(b)、9(b)和10(b)可知:角部边缘区域测点的脉动风压系数随湍流积分尺度的增加而略有增大,与实测结果更加接近;工况CBL-1的试验值小于CBL-1 and Active Gust工况,其差别主要由阵风风洞增加的低频湍流分量引起,表明在风洞试验中湍流积分尺度和低频湍流对锥形涡作用下的平坡屋面角部边缘区域的脉动风压影响显著,可通过准定常理论修正风洞试验未能模拟的低频湍流分量的影响。 图7 湍流强度对270°平均风向角屋面中轴线区域风压系数的影响 图8 湍流积分尺度对角部测点50101平均和脉动风压系数的影响 在CBL-1和CBL-2工况下,进一步比较分析各风向角下测点50101、50901和50209的风压系数,以区分湍流强度对角部测点平均风压系数和脉动风压系数的影响。如图11~13所示,在CBL-1工况下,50101、50901和50209测点的平均风压系数绝对值比CBL-2工况分别增大约14.8%、15.3%和13.9%,脉动风压系数分别增大约40.1%、37%和35.3%。对比2.3节中将湍流积分尺度作为影响因素的试验结果可以发现:与湍流积分尺度相比,湍流强度对锥形涡影响下的屋面角部边缘区域的风压影响更为显著,湍流强度起主导作用。因此,在低矮建筑风洞试验中,首先需模拟目标湍流强度;同时需修正湍流积分尺度对脉动风压系数的影响。 图9 湍流积分尺度对角部测点50901平均和脉动风压系数的影响 图10 湍流积分尺度对角部测点50209平均和脉动风压系数的影响 图11 湍流强度对角部测点50101平均和脉动风压系数的影响 图12 湍流强度对角部测点50901平均和脉动风压系数的影响 图13 湍流强度对角部测点50209平均和脉动风压系数的影响 在阵风风洞中开展了低矮建筑标模(TTU)1∶50刚性模型测压试验,研究了顺风向湍流积分尺度与湍流强度对屋面气流分离再附区域和锥形涡作用下的角部边缘区域的平均风压、脉动风压和峰值负压产生的影响,并与实测结果进行了对比,得到如下结论: (1) 基于阵风风洞,采用主、被动湍流相结合的方式模拟了平均风速剖面相同而湍流剖面有增大的不同近地流场;阵风边界层风场显著增大了顺风向湍流积分尺度,同时,横风向、竖风向湍流分量不受旁路主动控制的影响。 (2) 来流湍流强度对气流分离作用下的迎风屋面屋檐区域的平均风压系数、峰值负压系数和脉动压力系数的影响显著;湍流积分尺度对气流分离再附流动作用下的迎风屋面屋檐区域的平均风压系数影响甚微,对脉动风压系数有显著增大的效果,对峰值负压系数有一定影响。 (3) 湍流积分尺度对锥形涡作用下的屋面角部边缘区域的平均风压系数影响不大,而脉动风压系数随湍流积分尺度增大略有增大;与湍流积分尺度相比,湍流强度对锥形涡影响下的屋面角部边缘区域的平均风压系数、脉动风压系数的影响更为显著。 致谢:感谢国电环境保护研究院有限公司田文鑫工程师提供风洞试验帮助;感谢桂林理工大学研究生许俊、严赫绘制部分插图和表格。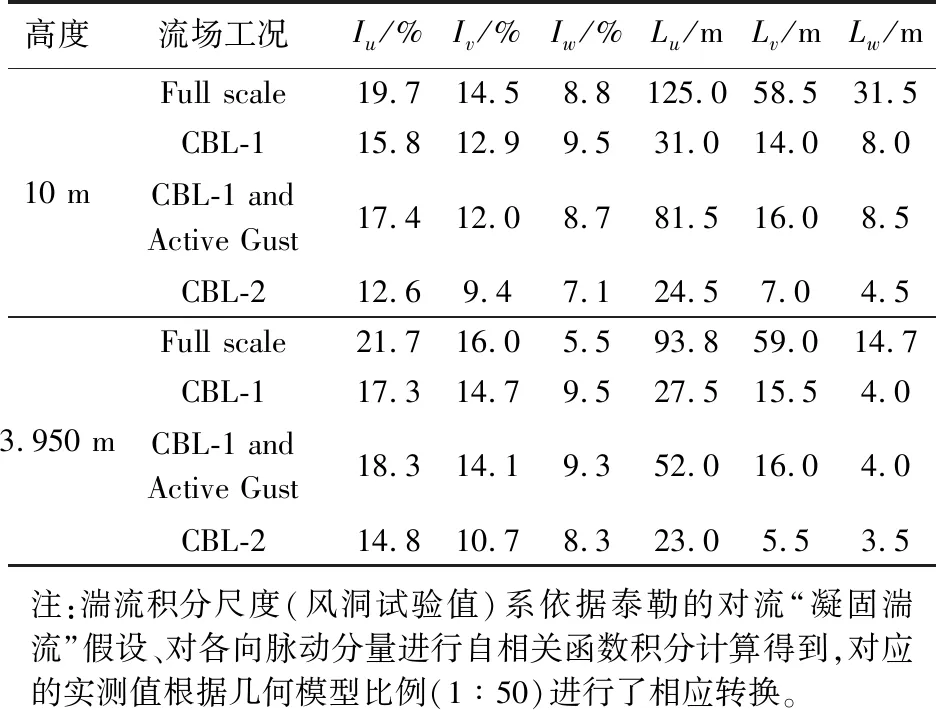
1.3 TTU标模测压试验
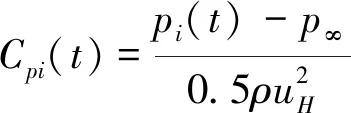
2 试验结果分析与验证
2.1 湍流积分尺度对屋面中轴线区域风压的影响
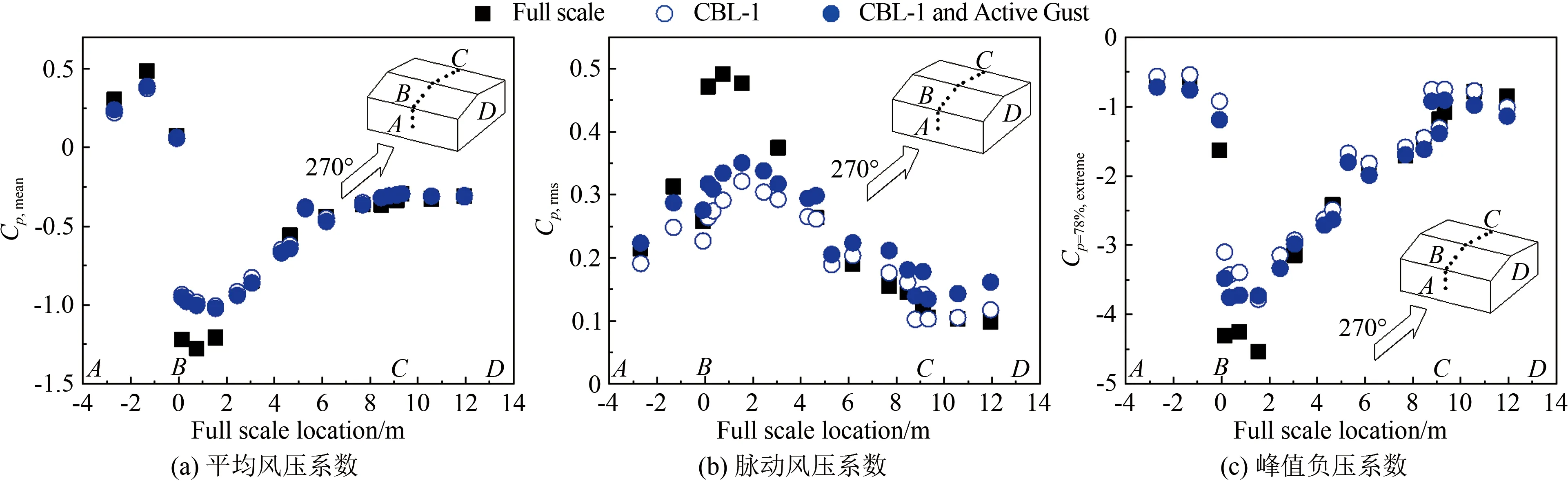
2.2 湍流强度对屋面中轴线区域风压的影响
2.3 湍流积分尺度对角部边缘区域风压的影响

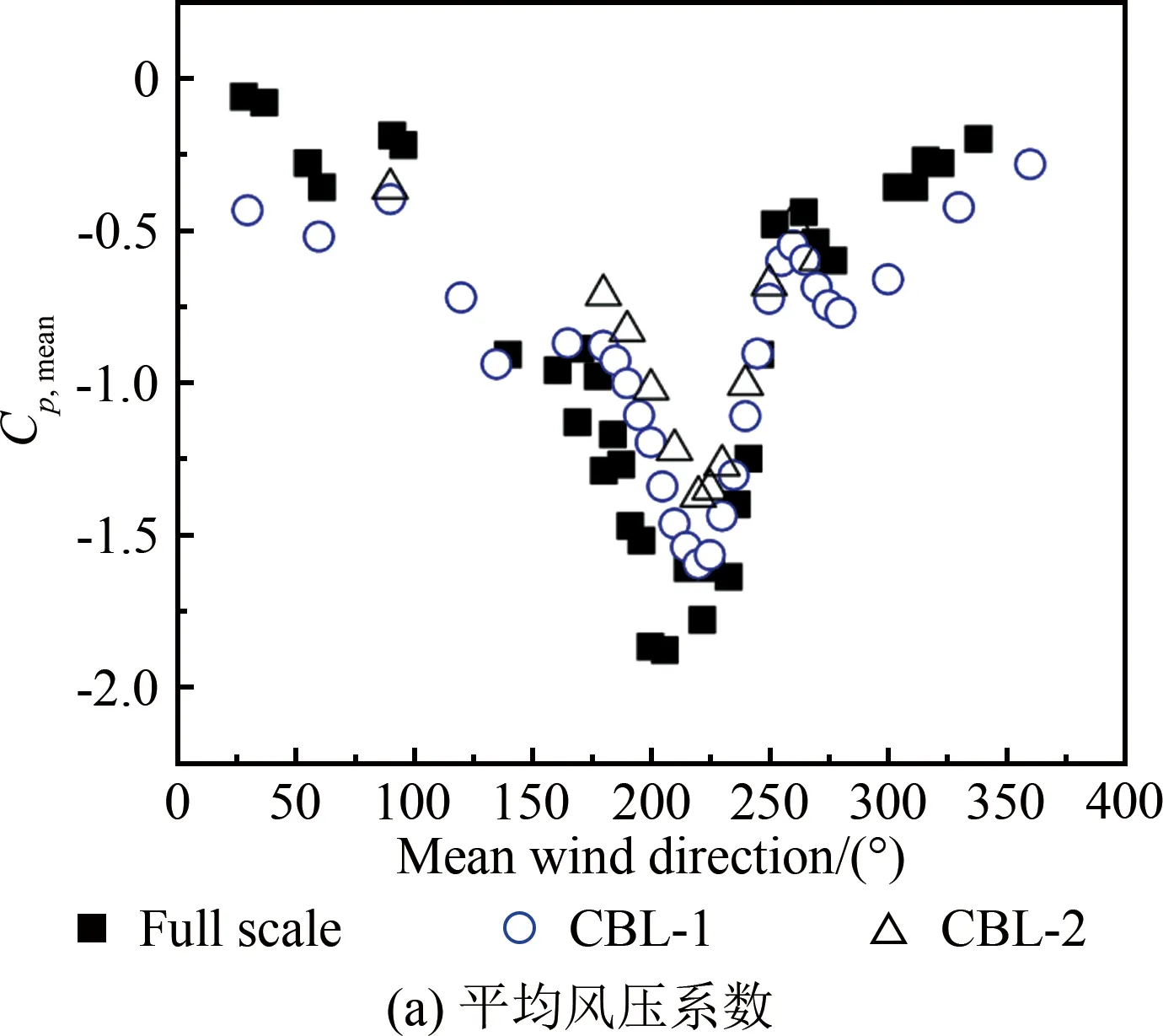
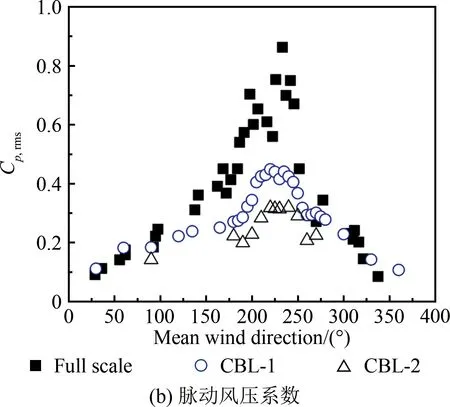
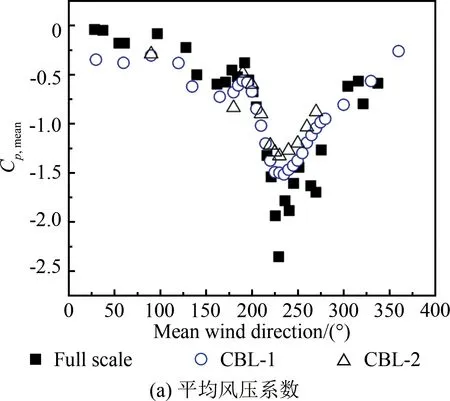
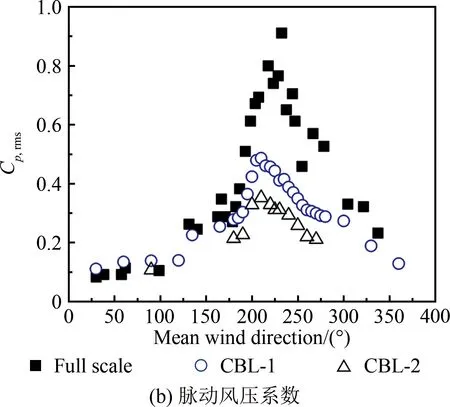
2.4 湍流强度对角部边缘区域风压的影响
3 结 论
