基于工业机器人的鞋帮打磨系统设计①

2020-09-18张立彬周邦达司云峰鲍官军

高技术通讯 2020年8期

张立彬周邦达沈遥司云峰鲍官军

(*浙江工业大学机械工程学院杭州 310014 ) (**起步(中国)有限公司丽水 323906 )

0 引言

全国制鞋工业信息中心的报告表明，中国仍然是世界鞋类最大的生产国和出口国，2017年共生产135.23亿双，世界产量占比57.5%，世界出口占比34.9%[1,2]。但随着制造成本的上涨、国外市场的反倾销以及东南亚制鞋产业的崛起，我国的制鞋产业遭遇了前所未有的危机[3]。人工成本上升趋势正在削弱我国制鞋行业贸易竞争力[4]，相较于2014年巅峰时期66%的世界产量占比，2017年产量下降幅度达到18.7%[5]。定位低端、劳动力密集的生产模式已经不利于中国制鞋行业的持续发展，自动化、智能化将成为中国制鞋业的主要方向[6]。中国制鞋厂商仍在采用的鞋帮手工打磨作业方式，正面临着用工成本攀升、健康问题凸显、良品率低等挑战，需要尽快实现自动化打磨的替代方案。

针对鞋帮自动化打磨的问题，国外已经有智能设备公司进行了长期的研究并设计了先进的设备。意大利CERIM公司设计生产的K176鞋底机，可以同时安装多种类型的刀具，能够适应加工不同形状和材质的鞋品，日加工工件数量达到1000双以上。但这类专用设备，往往价格昂贵，不适用于大部分企业。就制鞋业劳动密集这一特点而言，应用工业机器人进行生产线改造是个不错的选择[7]。国外也有公司研究工业机器人在鞋帮打磨中的应用[8,9]。20世纪 90 年代初，瑞士史陶比尔机器人公司就与法国自动化集成商丰雅公司合作设计了鞋品自动化成型线，使用史陶比尔的6轴工业机器人完成鞋帮底面的打磨、上胶、削边等工作。德国的鞋机制造商DESMA 也从1998 年开始设计并不断改进圆盘式机器人鞋底机[10]。

浙江省“机器换人”的大背景下[11]，考虑到工业机器人的硬件成本较低且具有较高的灵活性，能较好地完成复杂空间曲面的打磨工作，本文尝试用工业机器人开发一套鞋帮打磨系统。整个鞋帮打磨系统的设计围绕着打磨刀位点信息的提取、打磨控制指令的生成2个任务展开，前者借助UG二次开发工具实现，后者在研究机器人指令基础上用C++编程实现。最后搭建出打磨设备，在Qt上开发系统软件，自动生成打磨控制指令去驱动工业机器人，代替人工进行鞋帮自动化打磨作业。

1 打磨刀位点的描述及其转换

鉴于鞋帮打磨设备较为轻巧、打磨姿势需要不断微调等实际情况，同时也为了简化编程、夹具设计等工作，本文选择用工业机器人末端夹持的打磨设备对固定在工作台上的鞋帮底面进行打磨。传统的人工打磨作业由制鞋工人实时手动调整鞋帮与打磨设备之间的距离与角度。而使用工业机器人进行打磨时，必须预先定义好鞋帮底面的打磨点位，将其描述成机器人末端的位姿，并建立机器人关节的运动模型，将末端位姿转换成机器人关节的控制信号[12]，以备后续离线编程之用。

1.1 确定打磨刀位点的位姿

鞋帮底面打磨刀位点的描述就是对打磨工具位置和姿态的描述。如图1所示，规定机器人基坐标系为{B}，点P为机器人末端工具刀尖点的位置，则可以使用矢量BP表示刀尖点P在基坐标系{B}中的位置：

(1)

其中px、py、pz分别表示点P在基坐标系{B}中坐标轴XB、YB、ZB上的投影分量。

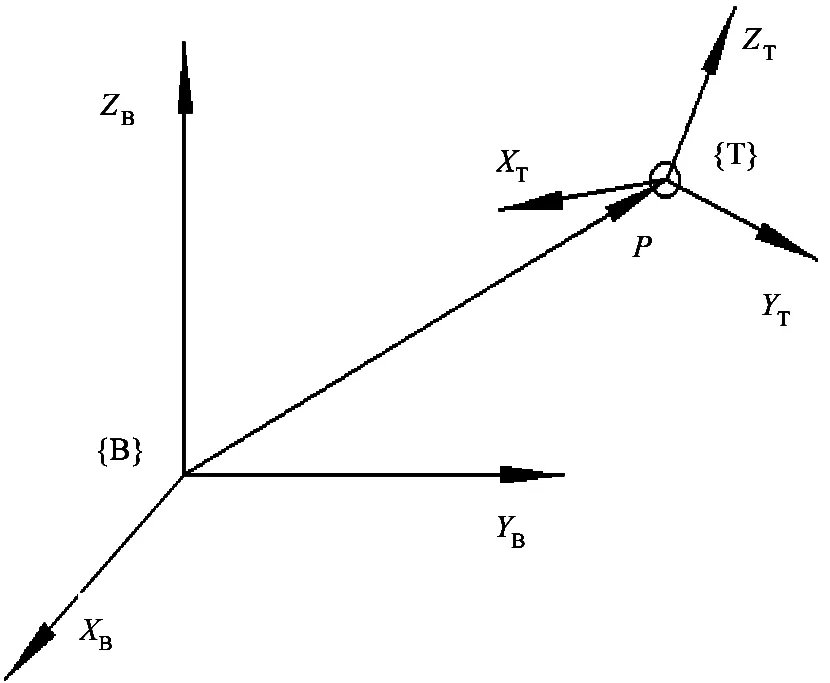
图1 机器人末端刀尖点的位姿描述

将坐标系{T}固连在机器人末端工具的刀尖点P上，则可以使用坐标系{T}的XT、YT、ZT正方向的单位矢量描述机器人末端工具的姿态。上述3个单位矢量使用基坐标系{B}来表达，分别对应矢量n、o、a，则坐标系{T}的位姿可以使用一个4×4的齐次变换矩阵A表示：

(2)

nx、ny、nz分别表示XT正方向的单位矢量在基坐标系{B}中XB、YB、ZB方向上的投影分量，矢量o和矢量a同理[13]。px、py、pz分别表示点P位置在基坐标系{B}中XB、YB、ZB方向上的投影分量。

综上，若要确定机器人末端工具的位置和姿态需要4个矢量。位置矢量就是点P的位置坐标矢量。不妨设机器人在打磨时末端工具的姿态由以下3个矢量决定，法向矢量N、切向矢量T及副法向矢量B。定义机器人末端工具在打磨点Pi处垂直于打磨曲面的矢量为法向矢量Ni，方向由鞋楦内部指向鞋楦外部。切向矢量T与法向矢量N正交，在打磨点Pi处与空间曲面相切。规定T平行于某一特定矢量，与机器人运动方向夹角小于90 °。副法向矢量B与法向矢量N、切向矢量T均正交，即满足下式。

Bi=Ni×Ti

(3)

1.2 建立机器人关节的运动模型

为了简化工业机器人复杂的几何参数，使用D-H(Denavit-Hartenberg)法建立本文选用的三菱RV-7F工业机器人的运动学模型(此处选择Modified D-H模型)，获得Modified D-H参数。

使用Modified D-H法建立的机器人运动学模型中，相邻关节间坐标变换矩阵的通式[13]如下：

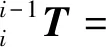
(4)

式中，αi-1是连杆转角，ai-1是连杆长度，di是连杆偏距，θi是关节轴的旋转角。

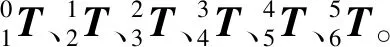
(5)

式(5)中，前3列矢量n、o、a，分别表示末端连杆坐标系{6}相对于基坐标系{0}的X0轴、Y0轴、Z0轴的单位矢量，3个矢量组成了一个连杆坐标系{6}相对于基坐标系{0}的旋转矩阵R，用以描述工业机器人运动时末端的姿态。最后1列矢量p表示末端坐标系{6}原点在基坐标系{0}中的位置，用以描述工业机器人运动时末端的位置。

借助上述转换矩阵可以根据向机器人伺服电机输入的各关节旋转角θi计算出机器人末端的姿态R和位置P(即运动学正解)。同样，使用几何、代数等方法也可以求得RV-7F工业机器人的运动学逆解。根据机器人作业位姿、关节活动范围等条件确定唯一逆解后，就可以通过机器人末端位姿信息反求机器人各关节的旋转角θi，从而获得各关节的运动控制模型。

2 打磨轨迹的规划及处理

上文描述了打磨刀位点矢量信息R、P到机器人关节旋转角θi的转换方法。接下来采用离线编程的方式进行打磨控制。第一步便是在鞋帮底面生成打磨轨迹，并获取鞋帮底面的打磨信息，进行一定处理后得到机器人打磨控制指令。

2.1 UG二次开发提取打磨信息

工业界中常使用商用的机器人离线编程软件如 SprutCAM、RobotMaster等对机器人的运动轨迹进行规划，由软件自身完成轨迹信息提取和运动程序生成的工作。鉴于商用软件价格昂贵、操作复杂、支持机型有限、利用率低等原因，此处选择使用UG及其二次开发工具UG/Open API来提取鞋帮底面打磨轨迹信息，整个流程如图2所示。

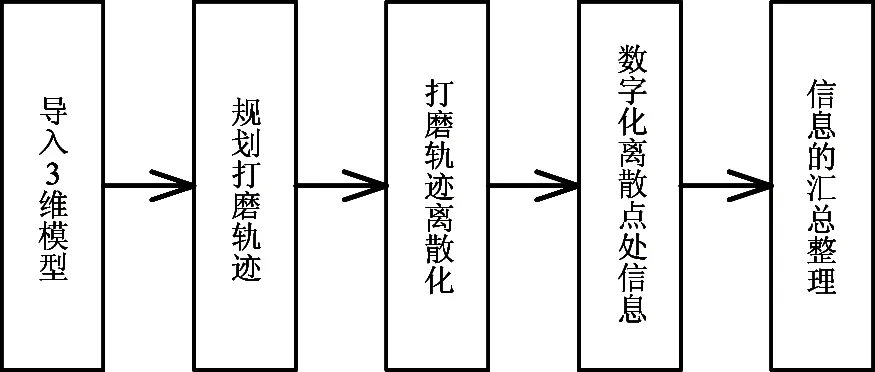
图2 打磨轨迹的生成与信息提取流程

2.2 获取打磨刀位点的位姿矢量

首先使用3维扫描仪对鞋楦进行扫描以获得精确的鞋楦3维模型并将其导入UG环境中。鞋楦实物与扫描得到的3维模型如图3所示。然后使用UG中的N边曲面造面功能对鞋楦模型底面上所有的NUBRS小面(如图4左图所示)按一定的公差进行删除重建，并将所有重建得到的N边曲面进行缝合使它们组成一个完整的鞋楦底面(如图4右图所示)。

图3 实验用鞋楦实物与3维模型

图4 鞋楦模型底面修改前后对比

接着用UG的抽取曲线命令获得图5曲线所示的鞋楦底面轮廓线。机器人鞋帮底面打磨轨迹曲线由鞋楦底面轮廓线偏置一定的距离dbias得到。偏置的距离dbias由鞋帮底面的宽度dbottom和打磨工具上磨头的宽度dtool决定。设打磨工具的刀尖点位于磨头的中间位置，则设定的偏置距离dbias和打磨工具上砂轮的宽度dtool需要同时满足以下条件：

(6)

图5 机器人打磨轨迹曲线的规划

当满足式(6)所列出的条件时，将提取出的鞋楦底面边线偏置合适的距离，得到如图6所示的机器人打磨轨迹曲线。

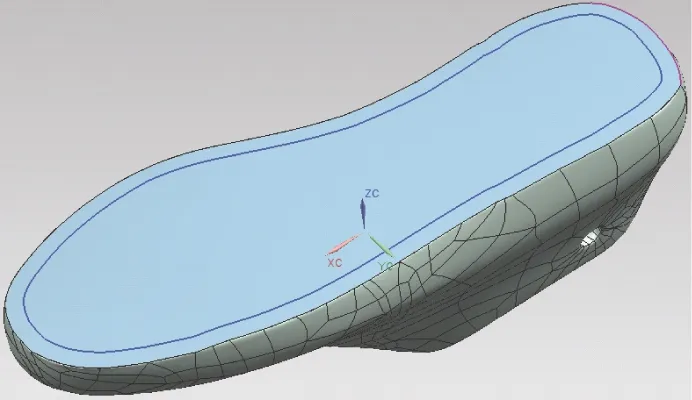
图6 生成的机器人打磨轨迹曲线

接下来调用UG/Open API中的离散化函数UF_MODL_ask_curve_point对用选择函数UF_UI_select_with_single_dialog选中的打磨轨迹曲线(图6所示)进行离散化，获得一定数量离散点的空间位置矢量P，流程如图7所示。此外还需要确定法向矢量N、切向矢量T以及副法向矢量B(即机器人末端的姿态矢量R)。将图6打磨曲面的句柄和上述离散化后获得的离散点坐标pts作为输入参数，输入到函数UF_MODL_ask_face_parm中，以获得所有打磨刀位点的U、V参数。最后将这些U、V参数连同曲面句柄依次输入到函数UF_MODL_ask_face_props中，直至提取出所有打磨刀位点的姿态矢量。整个流程如图8所示。

2.3 优化刀位点切矢量

用上述库函数UF_MODL_ask_face_props直接求取的切矢量T方向是固定的(如图9)，不适用于打磨鞋底时打磨方向始终处于变化状态的情况。为了解决UG/Open API函数只能提取固定方向上切矢量产生的问题，需要使鞋帮底面打磨刀位点处的切矢量在XOY平面上的投影尽可能满足图10的情况。可以通过曲线拟合的方法获得鞋帮底面在XOY平面上投影曲线的函数表达式，然后根据函数的导数求取对应的切矢量。

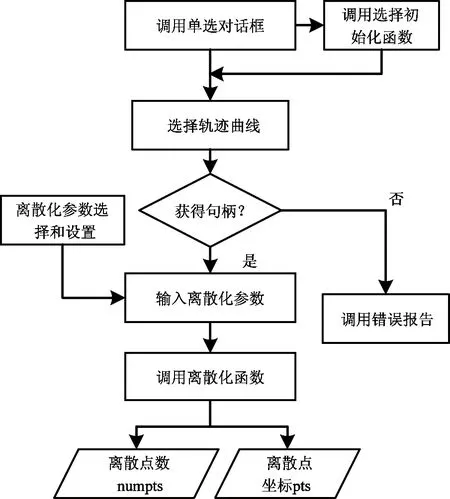
图7 打磨轨迹曲线离散化程序流程图

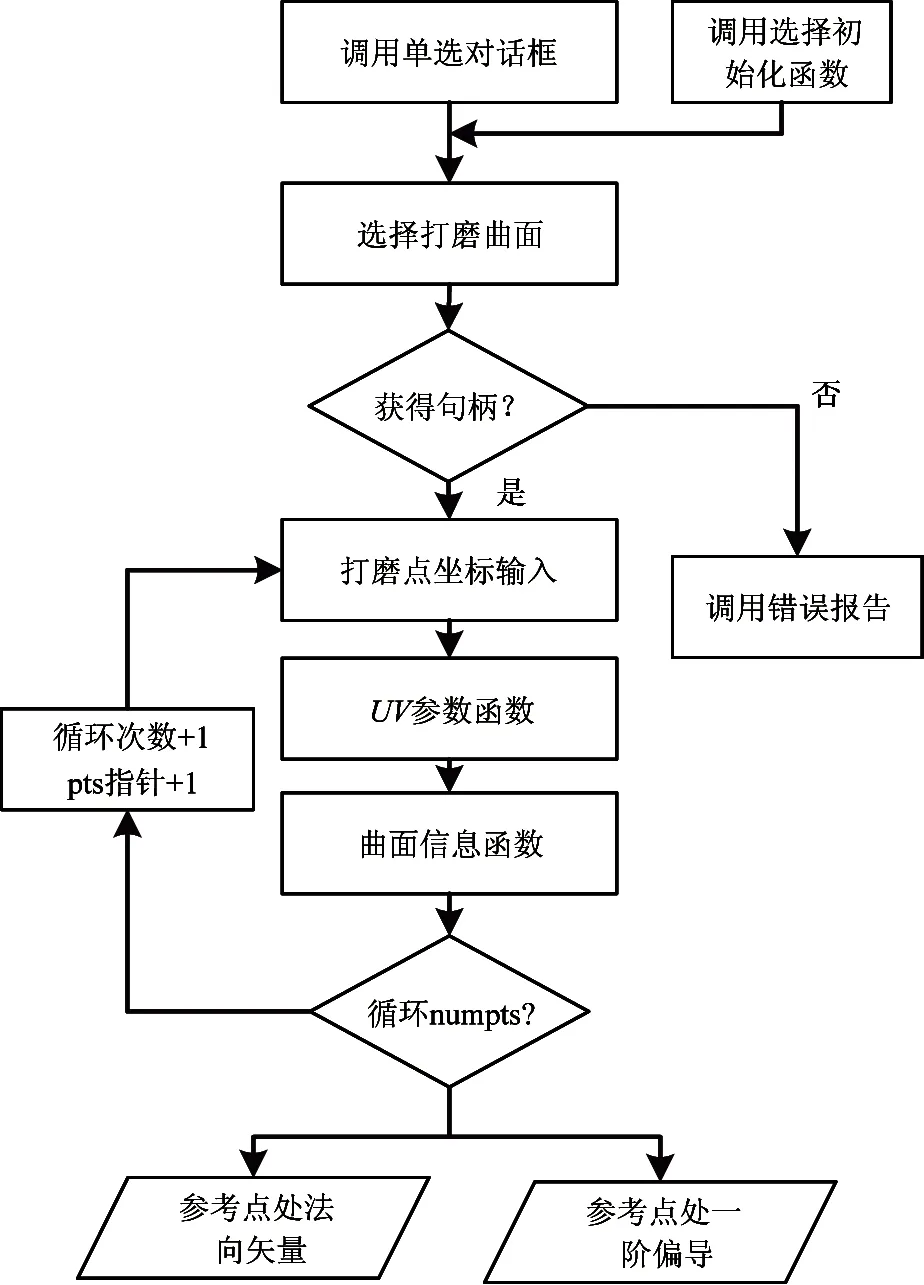
图8 打磨刀位点矢量信息提取程序流程图

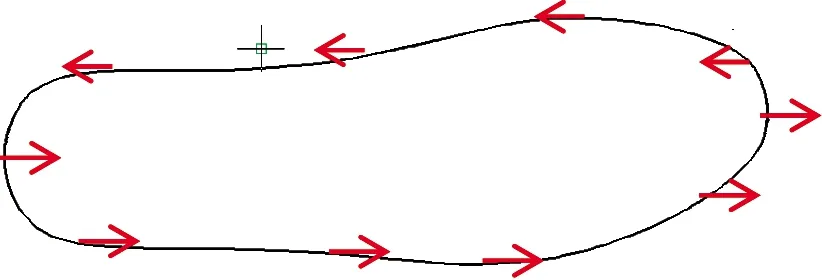
图9 单方向规划的切矢量

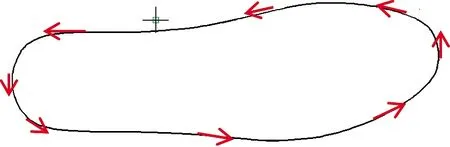
图10 较理想的切矢量规划

此处使用Python工具包Scikit-Learn拟合出了离散化后打磨轨迹左右2部分的8阶多项式曲线，如图11、图12所示。打磨轨迹右半部分的数学表达为

y=a8x8+a7x7+a6x6+a5x5+a4x4

+a3x3+a2x2+a1x+a0

(7)

根据式(7)容易得到拟合曲线的导数y′，从而可知打磨刀位点Pi处的规划切矢量：

(8)

其中，nxi、nyi、nzi为该点法向矢量Ni的投影。将Ti转换成单位矢量即得到该点的机器人姿态切矢量。同理，也能求得打磨轨迹左半部分打磨刀位点Pi处的规划切矢量：

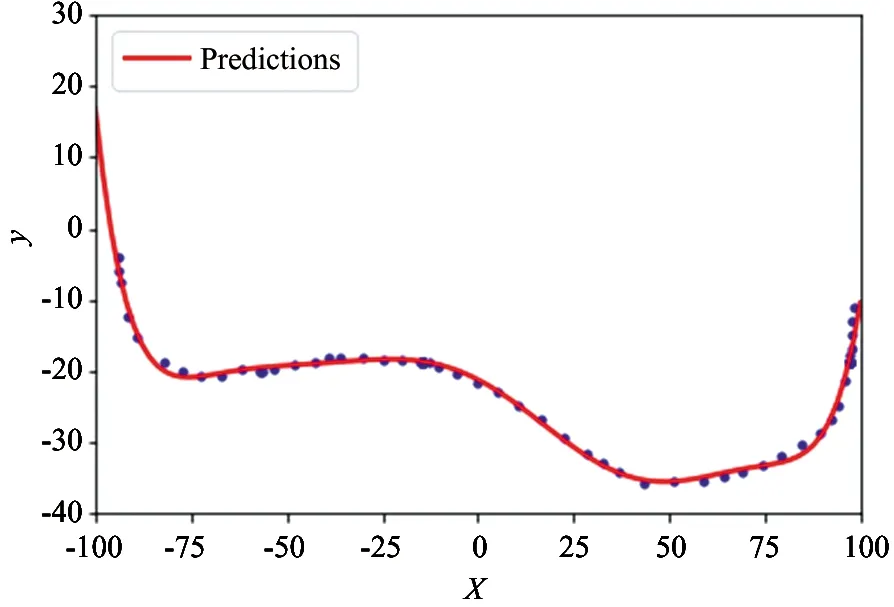
图11 8阶拟合曲线(右半部分)

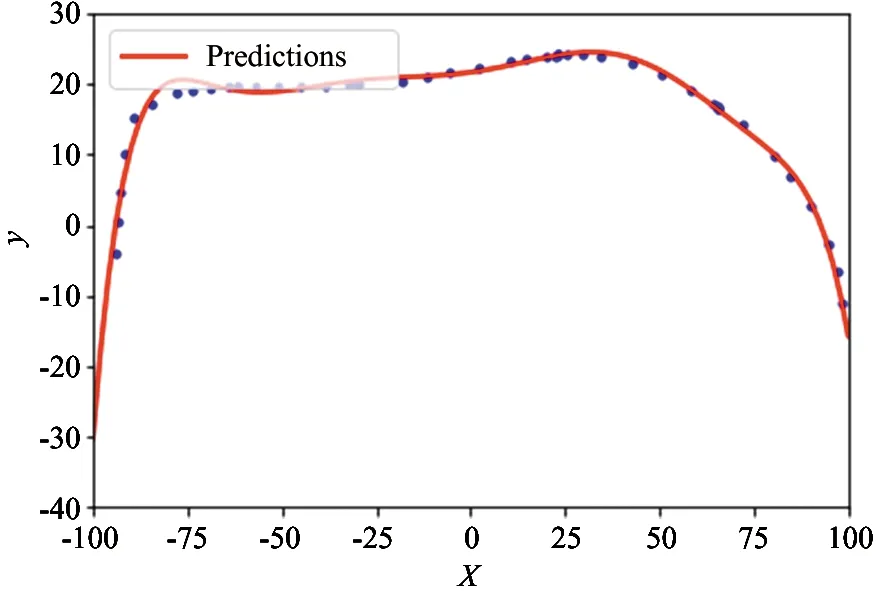
图12 8阶拟合曲线(左半部分)

(9)

经过这种方法规划后，机器人夹持的打磨工具的打磨方向不会发生突变，所以不必设置安全点来防止工具与工件的干涉；且打磨工具在打磨刀位点处始终与打磨轨迹在XOY平面上相切，因此打磨误差极小。

2.4 生成打磨控制指令

以上获得的打磨轨迹及各打磨刀位点的位姿矢量获取自UG环境，其坐标系与现实工件坐标系并不一致，需要对获取的打磨轨迹信息进行坐标系变换；再者仅依靠单纯的数据也无法直接驱动机器人，需要对轨迹信息字符串进行一定的设置以符合工业机器人控制指令与编程语言的语法要求。

2.4.1 偏置打磨刀位点坐标

如图13所示，假设鞋帮底面原料厚度为hbottom，指定的打磨深度为haim，则机器人打磨刀位点应该在提取得到的离散点的基础上向离散点处曲面法矢量方向上偏置为

hbias=hbottom-haim

(10)

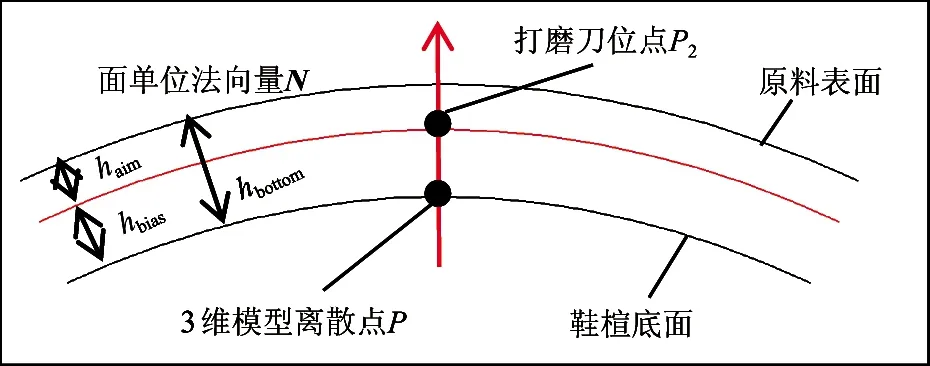
图13 实际的打磨刀位点与提取的离散点的关系

若提取的离散点Pi(xi,yi,zi)处的鞋帮底面单位法矢量为Ni(nxi,nyi,nzi)，则实际的打磨刀位点坐标值需要按照下式计算。

(11)

2.4.2 转换打磨刀位点坐标系

接着采用3点标定法进行坐标转换。先在鞋楦模型上选取不在同一条直线上的3个点AUW、BUW、CUW，并在鞋楦工件上标记对应的3个点A0、B0、C0，得到6个点的坐标值。此外，还能计算出由AUW、BUW、CUW3点确定的空间圆的圆心坐标OUW，以及鞋楦工件上对应的圆心坐标O0。

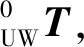
(12)

(13)

(14)

(15)

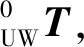
2.4.3 数据转换成控制指令

选择三菱工业机器人MELFA-BASIC V语言的直线插补Mvs指令作为机器人的运动控制指令，并选用直交型变量来输入驱动数据。直交型变量的参数由机器人位置数据X、Y、Z，姿态角数据A、B、C，附加轴数据L1、L2，结构标志FLG1和多旋转数据FLG2组成[14,15]。位置数据直接使用坐标系转换后的打磨刀位点坐标值，L1、L2、FLG2均设为0，根据打磨姿态FLG1设为7。至于姿态角数据，需要通过上述获得的打磨刀位点的姿态矢量来计算。不妨设末端旋转矩阵R为：

(16)

旋转矩阵中的3列即对应上文提取的矢量信息T、B、N。由此可得姿态角数据A、B、C：

A=atan(-r23/cosβ，r33/cosβ)

(17)

(18)

C=atan(-r12/cosβ，r11/cosβ)

(19)

3 鞋帮打磨系统的开发

3.1 搭建鞋帮打磨实验平台

设计的工业机器人鞋帮打磨工作站实验平台如图14所示，主要由运动执行部分(工业机器人RV-7F、运动控制器CR751-D)、力检测部分(6维力传感器4F-FS001-W1000套件)、打磨末端执行器系统(气动打磨机、打磨头、空气压缩机)、工作台、鞋楦工件以及其他配套设施组成。

图14 工业机器人鞋帮打磨工作站

3.2 开发打磨系统软件

为提高编程效率，工业机器人系统一般用Qt来开发[16]。如表1所示，本文采用C++编程语言，基于Qt图形用户界面应用程序开发框架来编写打磨系统软件[17]，主要编写3个模块即机器人运动程序生成模块、机器人运动参数设置模块和数据库操作模块。系统软件的总体设计框图如图15所示。

表1 鞋帮打磨系统软件开发环境

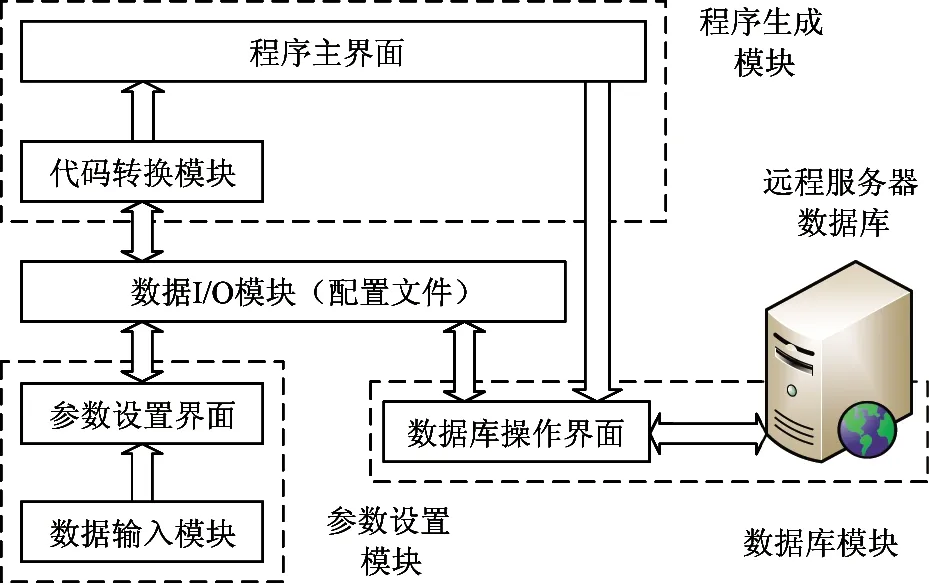
图15 系统软件的总体设计

机器人运动程序生成模块用于打磨刀位点数据文件的读取，并根据打磨参数自动将打磨刀位点转化为工业机器人运动控制指令；机器人运动参数设置模块用于交互设置坐标标定、刀位点偏置、工具坐标系设定等参数；数据库操作模块用于实现实验数据的存储备份及操作日志功能。

4 鞋帮打磨实验

4.1 鞋帮打磨实验

最后通过实验来验证机器人打磨工作站的可靠性以及系统软件中集成的各程序的正确性。选择图16所示的女式板鞋进行打磨实验，具体步骤如表2所示。

图16 实验工件实物图

图17 工业机器人鞋帮打磨实验

表2 鞋帮底面打磨实验步骤

4.2 实验结果与分析

4.2.1 打磨实验总体效果分析

某次机器人鞋帮打磨实验结束后的工件情况如图18所示，其余样品打磨效果相似，且多次打磨实验均能在计划的30 s内完成。实验过程中机器人运动稳定流畅，没有碰撞与振荡情况。

图18 执行打磨程序后鞋帮底面的情况

多次测试后，通过分析力传感器生成的日志数据，获得表3所示的打磨作用力实验数据。数据表明打磨过程中打磨工具没有与工件发生碰撞，并且工具能够较好地贴合于工件曲面进行加工。测量多个打磨成品的打磨深度，获得表4所示的打磨深度实验数据。数据表明所有刀位点的打磨深度均在期望打磨深度范围内，机器人打磨工作站基本能够达到期望要求。

表3 打磨作用力实验数据

表4 打磨深度实验数据

4.2.2 实验问题分析

尽管打磨实验总体效果不错，但实验仍存在2个主要问题，即位置反馈与位置指令存在偏差和实际打磨刀位点与理论刀位点存在偏差。

打磨工具打磨效率过低和空间坐标系转换存在偏差都可能造成位置反馈与位置指令的偏差。前者可以通过增加打磨作用力，提高打磨转速，更改打磨刀具材料或调整打磨深度等方法解决。后者同时也会造成实际打磨刀位点与理论刀位点的偏差。模型重建时引入的公差、标定时累积的测量误差都会造成坐标转换的偏差，无法避免，只能尽量减小误差的影响。