基于深度多步时空神经网络的电动汽车负荷时空动态负荷预测

张秀钊，王志敏，钱纹，胡凯

（云南电网有限责任公司电网规划建设研究中心，昆明 650011）

0 前言

2015 年在《中共中央国务院关于进一步深化电力体制改革的若干意见》中[1]，明确了新一轮电改，将破除电网企业“独买独卖”的模式，电力改革的新模式为电动汽车的发展带来了新的挑战和机遇，由于电动汽车用户需求和行为的不确定性与相互差异，未来大规模电动汽车充电负荷具有时间和空间上的随机性、间歇性和波动性等不确定特点，将给电网的安全运行和优化调度带来困难。为了分析电动汽车充电负荷带来的影响，以及为电动汽车广泛接入电网的调控策略制订打下基础，提供理论支持，要求建立有效的电动汽车充电负荷预测模型[2]。

电动汽车负荷预测主要分为两类，一类是采用数学模型模拟电动汽车充电行为，从而得出电动汽车负荷预测值的方法[3-8]，此类方法在综合考虑充电负荷的时空特性时数学模型太过复杂，难以保证预测精度。另一类是基于历史数据采用统计学习模型进行预测的方法，用模型学习历史数据的潜在规律，从而达到较好的预测效果。

电动汽车充电负荷预测的传统负荷预测方法有回归分析法、相似日法等；现代预测方法有基于神经网络的预测法、基于小波分析的预测法以及支持向量机（Support Vector Machine，SVM）预测法等。文献[9]提出一种基于大数据的电动汽车充电负荷预测方法；文献[10]提到一种基于时间序列距离测量方法的短期充电桩负荷预测模型，该方法根据负荷序列的和时间序列的距离测量来进行充电负荷的预测；文献[11-12]采用支持向量机对电动汽车进行短期负荷预测，并将最后结果与蒙特卡洛方法进行比较，该方法结果明显优于蒙特卡洛方法；文献[13]提出一种快速充电站的规划建设方法，首先采用共享最近邻聚类法(SNN) 来确定充电站位置以及充电站覆盖范围，然后采用排队论预测充电装容量进行定容；文献[14]提 出Modified Pattern Sequence Forecasting (MPSF) 和 Time Weighted Dot Product Nearest Neighbor (TWDP NN)两个算法在智能手机应用程序上进行电动汽车充电负荷预测，其中MPSF算法用于预测，TWDPNN 用于使得预测算法加速，该方法能很好的在手机上对电动汽车负荷进行有效的预测；文献[15]用时间序列模型对电动汽车负荷进行了预测，并采用了伯利克分校的实际充电负荷数据验证了模型的有效性；文献[16]提出了一种基于数据新鲜度和交叉熵的组合预测模型，并验证了该方法比单一模型的有效性。

过去的电动汽车充电负荷预测统计学习方法更多都是只考虑时间维度的预测方法，没有考虑电动汽车充电负荷所包含的复杂空间性。因此，综合考虑负荷的时间及空间双重动态变化，才能更好的进行时空动态预测。深度学习（Deep Learning, DL）作为机器学习领域一个重要的研究热点，已经在图像分析、语音识别、自然语言处理、视频分类等领域取得了令人瞩目的成功。在预测上也取得了一定成功，文献[17] 提出了一种深度时空残差网络用于预测北京市的空间人群流动情况取得了很好的效果。

综上所述，提出一种深度多步时空神经网络DMSTN (Deep Multi-Step Spatio-Temporal Neural Network)，该网络可以很好的学习到充电桩负荷的时空动态规律，从而从空间和时间上整体的对负荷进行预测。

1 电动汽车时空动态负荷矩阵

电动汽车负荷具有时间和空间上的随机性，为了更好的预测这种时空动态性，需要将充电桩上的负荷进行时空维度的刻画。根据充电桩位置将充电桩充电负荷用二维矩阵表示，并整理成时长T 的时空序列D{D1,D2,...DT},D ∈RT×X×Y，Dt为时间t 的电动汽车空间负荷矩阵见式(1)，其中是坐标为(x,y)点的负荷量。

图1 充电桩分布图

根据10 个充电桩的经纬度分布（见图1）建立一个负荷矩阵，构建二维负荷矩阵的方法为：

1）构建坐标轴，确定所有充电桩的坐标；

2）计算出每个充电桩负荷覆盖的范围，每个充电桩的覆盖范围是自己坐标为中心的一个正方（正方形边长由充电桩覆盖范围确定）；

3）将所有充电桩负荷覆盖范围内填上该时刻充电桩的负荷量并累加，得到该时刻的负荷矩阵。

2 建立时空动态负荷预测模型

为了预测未来K 个时间点的充电桩时空动态负荷矩阵，需要建立一个根据过去S 个时间点观测值，来预测未来K 个时间点的因果系统见式(2)，其中P(..) 代表一个因果系统，Dt代表第t 个时刻的预测负荷矩阵。

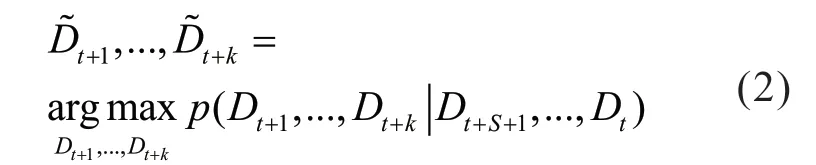
实验将STN (SPATIO-TEMPORAL NET WORK)[18]的结构修改为多步时空动态神经网络后用于构建该因果系统。

2.1 深度多步时空动态神经网（DMSTN）

2.1.1 ConvLSTM层

LSTM 通常用于解决一维时间序列的预测问题，无法考虑空间上的相关性。在此基础之上文献[18]提出了可以用于考虑时空两个维度的网络结构ConvLSTM，ConvLSTM 结构能够学习到长期的二维数据规律，这非常适合用于电动汽车动态负荷矩阵的预测。ConvLSTM 和LSTM 一样，将上一层的输出和新的输入作为下一层的输入。不同点在于加上了卷积操作之后，为不仅能够得到时序关系，还能够像卷积层一样提取空间特征。这样就得到时空两个维度的特征，并且将状态与状态之间的切换也换成了卷积计算。针对有一个二维充电时空动态负荷矩阵的时间序列的输入XT+{X1,X2,...,XT}，其中Xt表示t 时刻的负荷矩阵。ConvLSTM 的具体过程见式(3)。

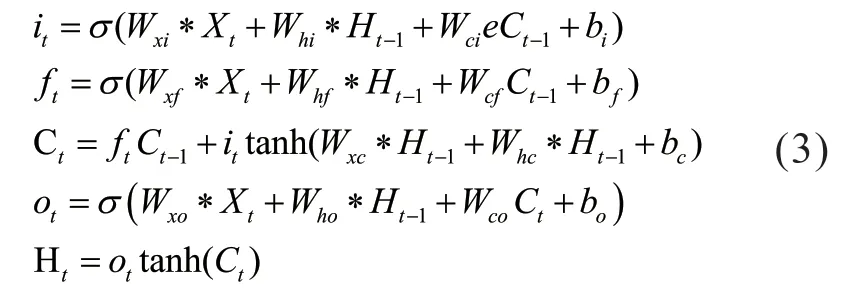
其中Wxf、bf表示遗忘门权重和偏置；Wxi、bi表示输入门的权重和偏置；Wxc、bc表示更新值的权重和偏置；Wxo、bo表示更新值的权重和偏置；σ(g) 代表sigmiod 激活函数、tanh(g) 代表双曲正切激活函数，“*”表示卷积计算，“⊙”代表Hadamard 乘法。

2.1.2 三维卷积层(3D-ConvNet)

三维卷积既可以捕获空间信息也可以捕获时间维度的信息。三维卷积核是将二维卷积核的扩充为三维，将数据根据时间维度堆叠为三维数据后进行卷积操作。针对有一个二维充电时空动态负荷矩阵的时间序列的输入XN={X1,X2,...,XN}，其中XN表示n 时刻的负荷矩阵，公式(4)给出了3D-ConvNet 层的与输出。

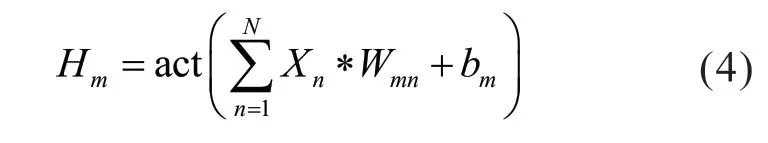
有M 个卷积核的3D-ConvNet 层输出由H1,...HM构成，act( ●)表示激活函数。三维卷积可以很好的学习时空特性，尤其是短时的二维数据规律，这可以很好的学习到由电动汽车用户随机充电行为引起的波动。

2.1.3 融合层

在实际的电动汽车时空动态负荷中，既有长期的充电负荷规律，也有短期由于天气、事件以及个人充电行为等随机性引起的短期充电负荷规律。为了同时学习到这两种规律，需要将三维卷积层的输出结果和ConvLSTM 层输出结果结合起来，因此建立一种融合层，其表达式见(5)。

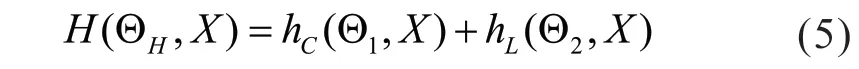
其 中hC、hL分 别 是3D-ConvNet 层 和ConvLSTM 层的输出，表示网络的权重和偏置。

2.2 时空动态神经网络结构

为了消除滚动预测带来的误差， 将STN(SPATIO-TEMPORAL NETWORK) 最后的输出部分改为3D-ConvNet，使得该网络能同时输出多个时间步数的时空动态负荷矩阵，因为网络是同时预测的多步矩阵序列是短时间序列，所以3D-ConvNet 层作为输出层可以更好的捕捉此类规律。假设输入为Ds={Dt-s,Dt-s+1,...Dt}，模型的用M 表示，该模型的所有参数用Θ 表示，则模型的表示见式(6)。

图2 多步时空神经网络结构

模型的整个网络结构见图2，采用将ConvLSTM 层和3D-ConvNet 层分别输出后用融合层进行融合的结构单元，能够全面的学习到长期规律和短期规律，多个单元的堆叠使网络的学习能力更强，3D-ConvNet 层作为输出实现多步预测。

3 时空动态负荷预测

3.1 算法流程

为了得到准确的负荷矩阵预测结果，需求解出该模型的最优参数，将该预测模型的目标函数设为(7),然后采用adam 自适应随机梯度下降算法求解该模型的最优参数。

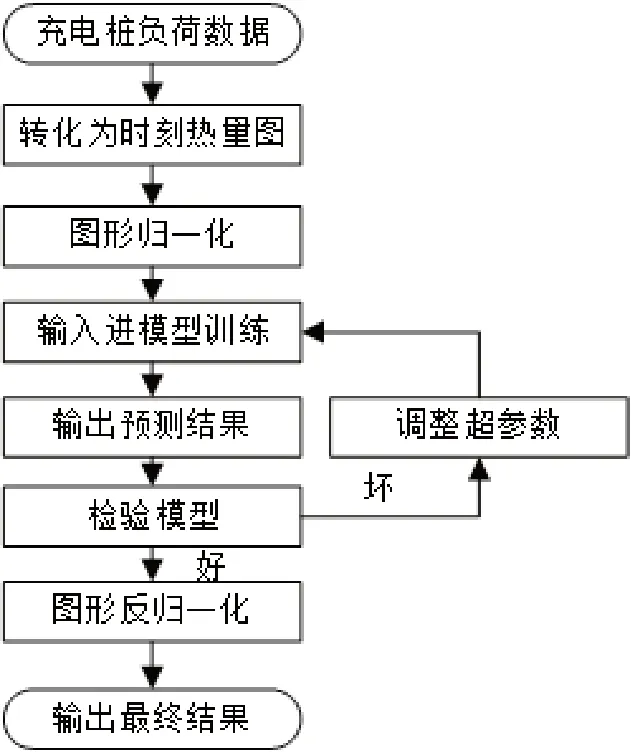
图3 算法流程图

模型的整个流程见图3，首先根据充电桩经纬度将建立充电桩平面分布图；然后根据历史负荷数据，按时间顺序在分布图上做出时空动态负荷矩阵；再将每个矩阵数据进行归一化；接着将数据输入进模型进行训练，根据训练结果调整模型的超参数，直到模型训练达到满意的效果；最后将图片数据反归一化并输出，得到最终预测结果。

3.2 评价指标

1）RMSE(Root Mean Square Error)：

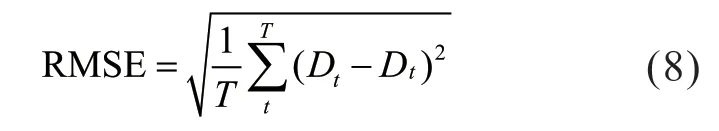
2）MAPE(Mean Absolute Percentage Error)：

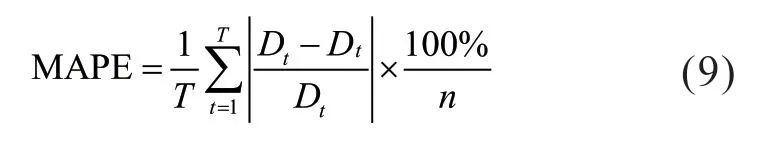
3）Coefficient of Determination：

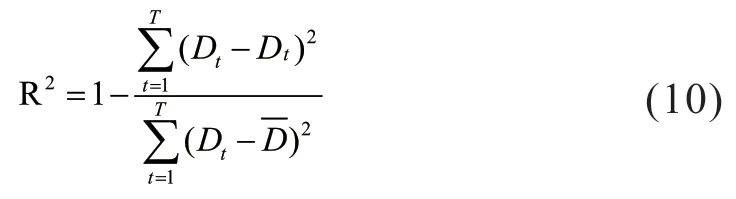
4 算例

采用某区域内实际充电桩充电负荷数据进行仿真实验，实验平台在深度学习框架Keras上进行，计算机条件是CPU:酷睿i7-7700、内存：16G、GPU：1080Ti 11G。

图4 充电负荷热量图

图4给出部分时刻充电负荷矩阵的可视化示例，颜色越深代表此处的负荷越大。并根据式(11) 将矩阵归一化，然后用DMSTN 模型进行训练和预测，将过去500 个时刻的负荷矩阵当作训练集，提前6 小时预测未来24 个小时的负荷矩阵，时间间隔为一小时，且模型采用过去48 小时的负荷矩阵当作输入，未来6 小时的负荷矩阵当作输出，最终实现同时预测未来6个时间步的多步预测。

将预测结果根据式(12) 进行反归一化，然后将图片输出。

为了找出模型的最优单元堆叠个数和体现模型的优越性，将分别用堆叠单元8-12 层的5种情况与STN 预测模型对比。表1 给出了两个模型在不同单元层数下的5 次实验24 个预测时刻的平均结果评价，包含了MAPE、MSE、R2三种评价指标。从中可以看出两个模型都是在单元层数为12 时模型能够取得最好的效果，以上三个指标的都是DMSTN 效果更好，可以看出DMSTN 模型具有更高的预测准确率。

选择了最优单元层数12 以后，最优预测结果和真实值进行对比。图中给出了24 个时刻的预测负荷矩阵，可以看出预测结果与真实结果比较一致，说明了该算法的有效性。

表1 DMSTN和STN的比较

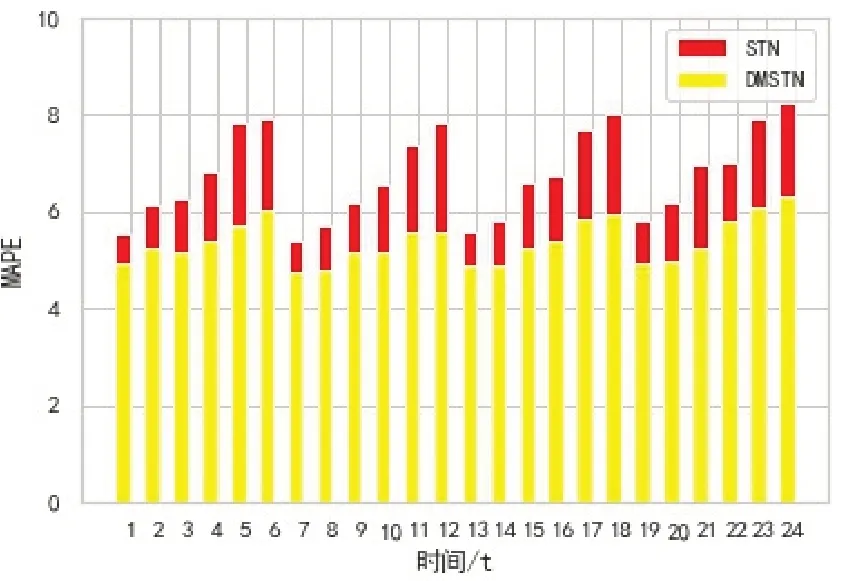
图5 误差对比

然后将预测误差MAE 与真实值的对比见图6，黄色代表DMSTN 误差，红色代表STN 误差。图中误差是提前6 个小时预测误差，所以误差周期大概为6。可以看出DMSTN 的每6 个预测点误差大小不会随着预测时间变长而慢慢变高很多，而STN 的误差是一直在递增的，除了前几个点的误差和DMSTN 相差不大，后面的误差越来越大，这充分说明了DMSTN 模型的多步预测，可以有效的降低滚动预测带来的误差。

为了验证DMSTN 算法的优越性，将其他5种算法做上述相同实验，得出表2 中6 种算法提前6 个小时预测未来24 小时的RMSE 数据，可以看出DMSTN 算法对比其他几种算法精度高出很多，由此验证该算法的有效性。

表2 不同算法间的比较

5 结束语

本文提出一种DMSTN 模型，用于解决电动汽车短期时空动态负荷问题，取得了一定的效果，对比STN 模型有更高的准确率。在12层单元时DMSTN 的MAE 和RMSE 误差平均值比11 层单元的STN 低18.32% 和33.72%，DMSTN 的R2得分比STN 高出8.53%。可以看出DMSTN 模型的预测精确度具有明显提升。对比其他几种算法进度也有很大提高。

该方法不仅可以消除滚动预测带来的误差提高预测精度，而且可以预测电动汽车充电负荷的时空动态，能给电网带来时空二维的负荷信息，更大程度的帮助电网解决充电汽车大量入网带来的问题。