基于相关性分析的高精度相位求取方法

章程 王景霖 徐丽清 沈勇 /1 中国航空工业集团公司上海航空测控技术研究所 2 故障诊断与健康管理技术航空科技重点实验室

0 引言

旋翼平衡对于直升机非常重要，旋翼的不平衡会加剧直升机的振动程度，造成飞行员的不适或直升机机械部件的磨损加剧[1-2]。相位是旋翼动平衡调整的两个关键参数之一，另外一个为调整量。通过相位和调整量可以得出旋翼系统的不平衡点，通过矢量分解和一定规则可以得到调整建议[3]。相位的不准确或者不精确会影响旋翼动平衡调整效果，严重时导致越调越差，甚至完全错误[4]。

为了获取高精度的相位信息，本文首先分析现有常用的离散傅里叶求取相位在速度和精度上的局限性，针对这些局限，从信号相位求取原理出发，研究出一种快速、高精度的基于信号相关性的相位求取方法，最后通过理论分析和举例说明验证本文提取方法的有效 性。

1 旋翼平衡调整分析

直升机旋翼由几片桨叶构成，由于存在桨叶规格不完全一致、装配误差等原因，在旋翼旋转平面上会有一个不平衡质心，如果这个不平衡质心较大或者偏离旋翼平面中心较远，将影响旋翼的工作性能，甚至造成旋翼无法工作。

由于不平衡质心偏离旋翼旋转中心，在旋翼的转动过程中，质心产生一个离心力，通过旋翼结构带动整个机体振动，振动过大时需要进行旋翼动平衡调整。通常是在质心关于轴心对称位置进行配重，以减低旋翼引起的振动，而配重的位置和大小通过振动信号的幅值和相位换算得到。通常的做法是在直升机旋翼附近位置安装振动加速度（速度）传感器、转速传感器，通过转速信号来截取振动信号，求取振动信号的相位和幅值。

为简要说明，可以通过振动加速度信号获取旋翼动平衡调整建议，需对旋翼转动进行受力分析，以一圆盘作为直升机旋翼转动平面的简化模型，分析不平衡状态下的振动信号的特点，如图1所示。在圆盘某个位置贴上反光条或磁片作为起始位置，在水平方向安装振动加速度传感器、光电或磁电转速传感器。

随着圆盘的转动，不平衡质心会产生一个离心力，使圆盘的轴心轨迹产生周期性的变化。为了更好地进行说明，假设圆盘的恒定转速为ω，圆盘/直升机整体质量为M1，不平衡质心为A，质量为m1，则质心A 在旋翼转动时产生的离心力F 为：

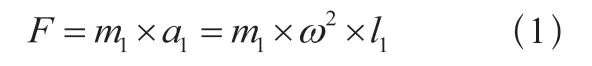
离心力F 带动整个直升机的振动，假设直升机整机的加速度为a，即加速度传感器采集的加速度a，则有

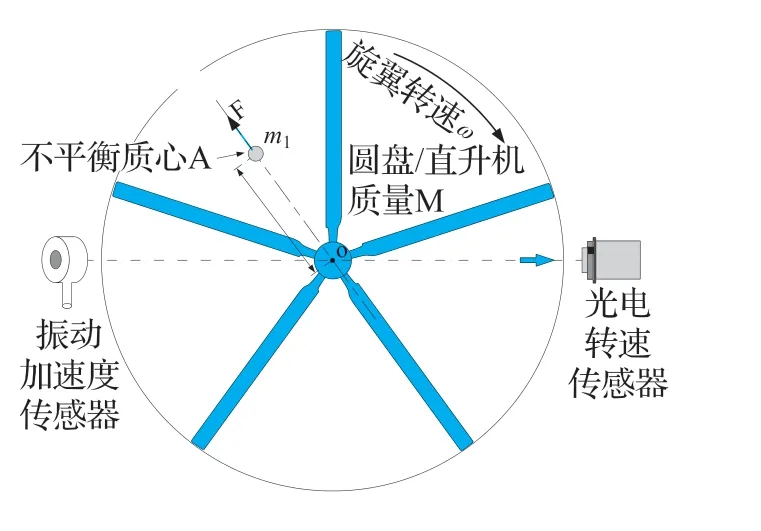
图1 圆盘不平衡状态受力分析

随着圆盘的转动，加速度a 呈现周期性变化，信号如图2 所示。然而在直升机动平衡调整测试过程中，实际采集的振动信号与转速信号可能不同步，旋翼转动平面（圆盘）不平衡质心转动产生的振动信号（能量）从振动源传递到传感器上可能需要一定的时间，这些都会导致信号延时，表现为一定的初始相位。虽然该相位和本文提到的相位求解有关，但由于该初始相位随着振动加速度传感器、转速传感器的安装位置的确定而确定，不会随着旋翼转动而变化，对本文求解相位影响很小，可以暂不考虑。

2 傅里叶变换求取相位的局限性

信号的相位通常是通过傅里叶变换求得。信号经过傅里叶变换后，通过联立对应的余弦系数（实部）与正弦系数（虚部）可以得到相位。由于计算机只能处理离散形式的数据，相位是通过离散傅里叶变换得到的。假设存在一个序列x（n），其离散时间傅里叶变换（DTFT）定义为：

逆离散时间傅里叶变换（IDTFT）定义为：

两组患者术前的空腹血糖值、餐后2 h血糖值及糖化血红蛋白值均相当，均差异无统计学意义（P>0.05）；两组患者术后的空腹血糖值、餐后2 h血糖值及糖化血红蛋白值均有显著改善，且改善程度显著优于对照组，均差异有统计学意义（P<0.05）。见表1。

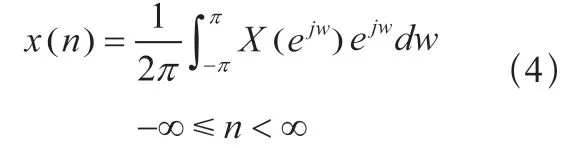
自然指数的幂级数ejw可以利用欧拉公式转化为正弦形式，欧拉公式如下：

式（6）的矩阵形式为：

从式（7）可以看出，傅里叶变换是以序列x（n）的长度作为一个周期（基频），然后构造与序列相同点数的1 倍频、2 倍频、…、K 倍频正弦函数基（实部为余弦，虚部为正弦），通过这些正弦函数基和序列相乘得出相关性系数，如图3 所示。将旋翼旋转频率（如w0）代入到式（7）可以得出此频率点上的实部与虚部，继而得到此点的幅值与相位φ0。

傅里叶变换求相位，首先会截取一定长度的采样数据作为序列x（n）（如210=1024 个点），但不能确保这段序列刚好是整数个周期（如图3 中的非整数周期）数据，因此对这种非整数周期数据做傅里叶变换求取相位是不准确的。假设存在一个采样率为100Hz、10个周期的余弦信号cos（x+30/180π），即此信号有30°的初始相位（见图4），然后对此信号进行截取，截取两个整数周期之间的数据点数，依次做傅里叶变换求取相位，验证由非整数周期数据做傅里叶变换求相位的不准确 性。

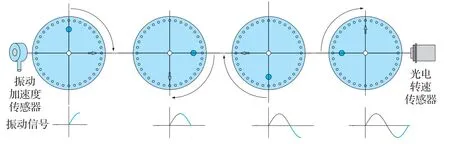
图2 圆盘转动状态下的振动加速度信号

图3 整数周期与非整数周期数据傅里叶变换

依次取5 个周期（500 点）～6 个周期（600 点）之间的数据，使用快速傅里叶变换（FFT）求取相位，得到的相位如图5 所示。从图5 可以看出，取整数周期数据（500 点、600 点）做FFT 求取的相位为30°，为正确的相位，但取500 和600 之间非整数周期做FFT 求取相位会得到不同的相位值。以上分析说明，对非整数个周期的信号做傅里叶变换求取相位存在缺陷，将得到不准确的相位。另外，对有限个数据点做傅里叶变换只会得到一定的相位分辨率，最终求得的相位精度 有限。

在旋翼动平衡调整中，某些设备通常是采用FFT 求取相位的。由于旋翼转速不稳定，每次取的数据点数并不能保证都是相同的周期数，导致用FFT 求取相位存在一定的误差。因此，在旋翼动平衡调整中，即使是对同一状态试验，用FFT 求相位也会得到不一样的 结果。

图4 采样率为100Hz、10个周期余弦信号

3 基于相关性的高精度相位求取

3.1 高精度相位求取原理

傅里叶变换原本就是求信号与余弦、正弦函数集合的相关性系数，为此相位求取可以通过与余弦、正弦函数做相关性分析得到。另外，由于直升机旋翼等旋转部件的位移、速度、加速度信号是周期性的，这些信号的相位可以通过与标准正弦信号做相关性计算得到。通过平移标准正弦信号与被测信号做乘积，即两个信号的卷积，可以得到周期性的相关性系数，当相关性系数最大时，标准信号的相位即为被测信号的相位，如图6 所示。

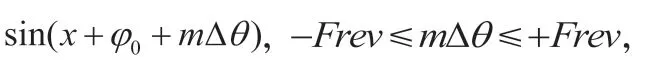
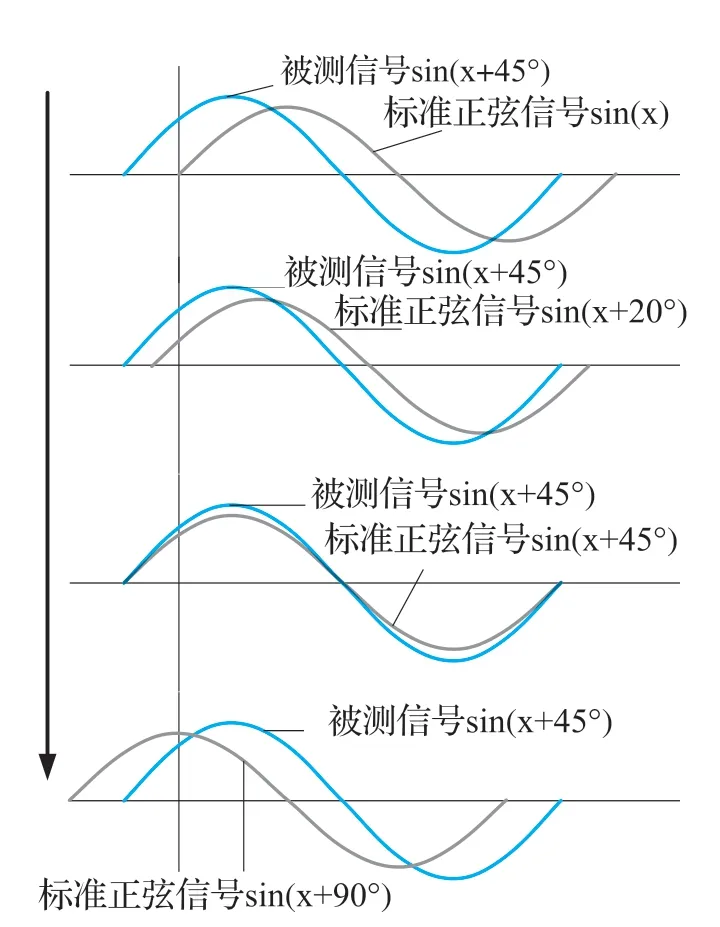
图6 通过相关性系数求取相位

图7 高精度相位求取示意图

3.2 基于相关性的高精度相位求取过程

在傅里叶变换求相位过程中计算所有频率点的值会占用一定的计算时间，但旋翼平衡调整中只需要求取旋翼转动频率点的相位，这导致傅里叶变换大部分的计算结果是用不到的。傅里叶变换是求信号和余弦信号、正弦信号的相关性系数。为此，针对旋翼动平衡调整中相位的计算问题，可以通过构建一组特别的余弦、正弦信号，先通过与余弦、正弦信号求相关性系数取得初步相位，然后微调具有初步相位的正弦函数的平移步长，求最大相关性以获取高精度的相位，具体步骤如下。

1）截取信号的整数个周期的数据：在旋翼平衡调整过程中，先通过转速信号换算出旋翼转速ω，并通过转速脉冲数据截取旋翼M 个整数旋转周期、包含N 个数据点的振动加速度信号，通过异常点剔除、滤波等预处理，得到信号为xInt。

2）求取相关性系数：构造M 个周期的包含N 个数据点的零相位余弦信号xcos与正弦信号xsin，通过式（6）求xInt与xcos、xsin的相关性系数。

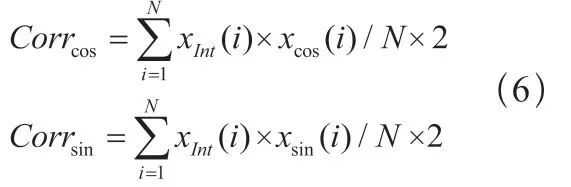
3）初步相位求取：通过反正切函数计算，并根据相关系数［Corrcos，Corrsin］所在的象限，可以得到在0°～ 360°的初步相位值φ0。

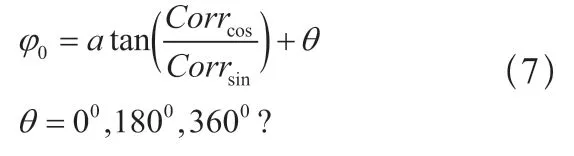
根据［Corrcos，Corrsin］所在象限得到

4）高精度相位求取：构建具有初步相位φ0的正弦信号sin（x+φ0），在一个正负相位分辨之间，逐步平移此正弦信号，求与振动加速度信号xInt的相关性系数，假设在sin（x+φ0+mΔθ）时取得最大相关性系数，则此刻正弦信号的相位φ0+mΔθ 为该被测信号的相位。

4 相位精度分析与验证

受计算速度的限制，傅里叶变换通常只取有限个数据点，只能得到一定的频谱分辨率和一定的相位分辨率。例如，某信号为y=sin（x+30.1°），一个周期抽样1000 个点，则一个周期360°对应1000 个点，相位分辨率为360/1000=0.36°，经过FFT 后，求取相位为30.24°，而不是30.1°，具体原因为：

1）相位分辨率：360/1000=0.36°；

2）具体点数：30.1/0.36= 83.6111，FFT 变换后只能取最接近的整数为84；

3）求取的相位：84×0.36= 30.24°。

使用傅里叶变换（如FFT）求相位的方法得到的相位分辨率为360°/ 1000=0.36°，如采用本文提出高精度相关性求相位方法，当Δθ 取360°/ 10000=0.036°，求得相位的精确度是FFT方法的10 倍。

特别是当一个周期内数据点不多时，高精度相关性求相位方法相比于FFT 求相位在相位精度的提升上将会非常明显。例如，一个周期只有83 个点，这时FFT 的相位分辨率为360°/ 83=4.3373°，但利用高精度相关性求相位方法可以取Δθ=360°/1000=0.036°，相位求解精度提高了12 倍多。这说明本文提出的方法能够显著提高低采样率情况下的相位精度。

5 总结

处于工作时的旋转部件如直升机旋翼通常转速不恒定，即使转速恒定也不能保证为做FFT 而选取的数据刚好为整数个旋转周期。对非整数周期数据做离散傅里叶变换求取相位存在不确定性，同时受数据点数的限制，求取的相位精度有限。为此，本文从信号求相位原理出发，根据转速脉冲取整数个周期的信号，与同样整数个周期的标准余弦信号、余弦信号做相关性求取初步相位，构造整数个周期、具有初步相位的正弦函数，在正负一个相位分辨率之间，微平移该正弦信号与被测信号求最大相关性系数，从而得到高精度相位。通过分析和案例验证，本文提出的方法具有两点优势：1）不需要FFT，只需要和正弦、余弦信号求一次相关性系数就可以得到用FFT 求得的初步相位，计算量大大降低；2）根据需要，设计微平移步数长度，可以得到高精度的相 位。