断裂的临界能量条件

林大超，徐 谦，王仲琦，刘海波

(1. 华北科技学院 建筑工程学院，北京 东燕郊 0652012. 北京理工大学 爆炸科学与技术国家重点实验室，北京 100081)

0 引言

断裂是一类十分常见的材料和结构受载破坏现象。由于断裂可能引发的灾难性后果，长期以来，它在理论和应用研究两个方面都得到了相当广泛的关注[1]。相关工作可以粗略划分为三个理论框架范畴，包括：建立在宏观现象观测结果基础上的材料力学理论[2]，以宏/微观缺陷(裂纹)作为控制要素的断裂力学理论[3]，以及立足破坏演化过程细/微观机制的材料物理力学理论[4]。不过，这种划分倾向于强调物理现象观测尺度间的差异。事实上，无论观测尺度如何，它们之间的融合已经成为理论发展的必然趋势。更为重要的是，外力作用能量的耗散既是其共同的客观事实基础，也是深入认识断裂发生规律的核心所在[5]。

Maxwell最早注意到通过能量描述建立材料破坏准则的可能性[6]。他的预言被后来发展起来的Mises屈服准则所印证[7]。虽然屈服和断裂属于两种不同的材料变形破坏形态，但实验观测结果表明二者的强度变化具有相似的函数关系[8]，因此，Mises准则也被用作为断裂判据[9-11]。主应力空间中沿等斜面(即八面体面)滑动的剪切弹性应变能，即形状畸变能，揭示了Mises准则屈服函数与变形能相互关联的物理含义。它也可以用于阐释断裂发生的能量耗散和转化条件。遗憾的是，这个能量表述没有考虑到滑动面上正应力(或静水应力)的影响[12]。

为了解释材料表观强度远小于理论强度的事实，Griffith提出了一个断裂理论模型[13]。这个模型明确了材料强度与其内部缺陷的密切联系，用裂纹-材料系统表征了裂纹扩展时外力作用的能量耗散关系。当系统储存的弹性能达到新生裂纹形成所需的表面能时，裂纹处于临界扩展状态。裂纹扩展时，系统的弹性能降低，其降低部分即为新生裂纹的表面能。Griffith模型理论上的严密性及其数学推演过程的一般性为断裂力学理论的诞生奠定了基础[1,3]。此后，应力强度因子和脆性断裂K准则[14]，D-M模型[15]和裂纹张开位移COD准则[16]，J积分[17]、HRR理论[18,19]和J积分断裂准则[20]等的提出，逐渐坚实了断裂力学的基本理论框架。与此同时，它们也开启了断裂力学理论深入于各种断裂现象分析的道路。如今，无论在宏观还是微观层面，只要谈到材料断裂强度，若没有应用断裂力学理论进行分析，似乎都容易被认定为是缺乏创新性的工作[12]。然而，对于那些不存在或者不考虑初始裂纹或几何奇异性的材料，它们的强度该如何分析处理？迄今，断裂力学理论还没有给出明确的回答。

初始裂纹是构成断裂理论模型的基本要素。是否可以放宽这个要素的要求？有研究针对这一问题，在Griffith能量耗散(守恒)概念的基础上提出了探索[21-23]。它们将所考察的弹性变形能储能体系退化到有限微分体积内，但是相关工作尚未发现突破性认识的迹象。如果将问题继续退化到任意物质点，能量耗散关系又将呈现出哪些特点？它是否可以为材料断裂认识提供新的视角？为了回答这些问题，我们提出了本文的研究工作。

断裂面上一点处储存了贡献于破坏运动的弹性应变能。假设它完全耗散于该点破裂发生所需的表面能，于是，可以从能量守恒关系获得一点处断裂的临界能量条件。本文通过两种岩石侧限(三轴)压缩的实验结果证明了这个能量条件的正确性。这个结果可望为无初始裂纹或几何奇异性材料的断裂强度分析提供新的基础理论认识。

1 断裂面上一点的能量分析

在断裂发生的临界时刻，断裂面依然属于完整的承载面。断裂面上一点分别受到沿法线方向的正应力σn和位于断裂面内的切应力τn的共同作用。断裂一旦发生，裂纹面随之形成，这两个应力分量也将因破坏变形的显现而卸除。在这个过程中，储存于破坏面的弹性能得以释放，并转化为新生裂纹的表面能。因此，断裂面上一点的弹性能与裂纹表面能之间的守恒关系确定了一点处断裂(开裂)发生的临界能量条件。

其实，断裂面上一点处切应力所存储弹性应变能的物理概念十分清晰。它代表了该点处位于断裂面内的切应力τn关于弹性切应变γn的变形势能。然而，正应力的能量贡献尚未见到理论上的明确论述。就一点处的变形而言，除去形状畸变变化外，剩余的变形成分应该是尺寸相关的体积变化。这里，形状畸变已经由弹性切应变γn给定。事实上，真实的断裂面并不恰巧对应于主应力(变)空间的等斜八面体面。但是，只有在等斜八面体面上，沿法向方向作用的正应力(变)才与体积应力(变)具有完全的对等关系。它意味着切应变γn所主导的变形分解不属于完全解耦形式[24]。也就是说，不是所有的弹性变形能都构成断裂发生的有效作用能。

在断裂面内，体积应变εV叠加了影响到剪切变形运动的成分。这个变形成分属于同一个方向上两个彼此相向的运动。由于切应力具有固定的作用方向，因此它们不会储存附加的变形能。沿断裂面法向，体积应变εV与正应力σn在正反两个方向同时发生作用，能够存储体积变形能。它们确定了破坏面上正应力σn的能量贡献。显然，拉应力σn促进断裂面的形成，提供的是正的断裂能。与此相对地，压应力σn抑制断裂面的形成，提供的是负的断裂能。

可以看出，断裂发生前，断裂面上一点所储存贡献于断裂的弹性应变能包含了剪切能和体积能两个部分。其中，剪切能由切应力τn关于弹性切应变γn的变形势能所确定，体积能由正应力σn关于体积应变εV在两个相向作用方向的变形势能所确定。据此，有

(1)

式中，e表示一点所储存贡献于断裂的总有效弹性应变能，μ和K分别为材料破坏卸载的剪切弹性模量和体积模量，σV为体积应力。绝对值符号的引入在于区分正应力性质相关的体积能的正负。体积应力与三个主应力分量σ1、σ2和σ3有关系，σV=σ1+σ2+σ3，它同时表示了应力状态的第一不变量。

在主应力空间(σ1≥σ2≥σ3)中，若断裂面的法线方向余弦为l1、l2和l3，应有

(2)

(3)

这里，法线方向余弦各分量应满足条件：

(4)

将式(2)～(4)代入式(1)，可得

(5)

式中，参数k为

k=μ/(3K)

(6)

真实的断裂应该发生在有效弹性应变能最大的面上，它要求

∂e/∂l1=∂e/∂l2=0

(7)

由此得到

(8)

(9)

注意到l10，这个方程组有解

(10)

这个结果确定了破裂发生的位向。将其代回式(5)，得到一点处的断裂能eF为

(11)

2 临界能量条件

若材料的单位表面能为γs，断裂所形成两个裂纹面的总表面能应为2γs。根据能量守恒原理，断裂发生时，弹性断裂能eF转化为裂纹面的表面能。因此，断裂的临界能量条件为

eF=1/(8μ)[(σ1-σ3)2+4k|σV|(σ1+σ3)

(12)

在纯剪应力状态下，有σV= 0，由式(10)知，断裂面位向与最大剪应力面一致。若材料纯剪破坏强度为τ0，由式(12)，知

(13)

它表明材料的表面能可以借助其纯剪强度得到确定。将式(13)代回式(12)，整理后，有

(14)

于是，我们得到了以物质点为考察对象时，外力作用能转化为裂纹表面能的能量耗散关系。这个能量耗散关系描述了一点处断裂发生的临界能量条件。它与Mohr-Coulomb准则力学模型的一个能量描述关系的推导结果基本一致[25]。不同之处在于，这里将问题上升到了整个应力空间。

临界能量条件(14)包含了两个材料参数，τ0和k。参数τ0代表了材料的纯剪破坏强度。它是一个材料常数。参数k由式(6)给出了定义。它与材料在断裂发生时刻的剪切弹性模量和体积模量的比值相关。由于剪切模量随应力状态的变化不是十分显著，因此可以将其假设为常数。不过，强烈的拉伸或者压缩载荷会使体积变形相当困难。此时，体积模量不再是常数。它表明参数k不能被简单地视为一个材料常数，而是应力状态相关的可变材料参数。因此，当参数k尚不明确时，临界能量条件(14)并不能直接用作断裂判据。

单轴(简单)拉伸和压缩具有相同的变形特征。不妨假设它们也具有相同的参数k，设为k0。单轴拉伸时，σ1=σV=σT，σ2=σ3= 0，其中，σT为拉伸断裂强度，从临界能量条件(14)，得到

σT=2τ0/(1+2k0)

(15)

此外，由式(10)的第一式可以发现，破断角(断裂面与拉伸力作用面间的夹角)θT满足关系

(16)

显然，这个角度应小于45°。单轴压缩时，σ1=σ2= 0，σ3=σV=σC，这里，σC为单轴压缩强度，临界能量条件(14)给出

σC=2τ0/(1-2k0)

(17)

由式(10)的第一式得到，破断角(断裂面与压缩力作用面间的夹角)θC满足关系

(18)

不同于拉伸断裂情况，单轴压缩的破断角大于45°。

3 分析与讨论

不同于断裂力学中的裂纹—材料系统模型，上述临界能量条件所考察的对象属于物质点。它表征了断裂发生或裂纹扩展时外力作用的能量耗散关系。虽然这个关系属于严格的理论推导结果，但它所能反映的材料断裂强度变化规律仍值得进一步考察。

3.1 参数k

参数k不能被简单地视为材料常数。它构成了临界能量条件(14)推广应用的主要困难。为了对参数k有更深入的理解，这里以岩石三轴压缩为例展开分析。

按照岩石力学的约定，取压应力为正，拉应力取为负，式(14)的临界能量条件改写为

(19)

利用式(17)，将τ0替换为σC，上式可以表示为

(20)

在这个表达式中，σC可由单轴压缩试验直接确定。若单轴拉伸或压缩断裂破坏的剪切弹性模量和体积模量均为已知，易于根据定义式(6)得到参数k0的值。其实，参数k0也可以根据单轴压缩或拉伸的破断角计算确定。以单轴压缩为例，若破断角为θC，由式(18)，有

k0=0.5-cos2θC

(21)

此外，如果单轴拉伸和压缩强度均已给定，依据式(16)和(17)，也可以得到

(22)

当σC和k0确定后，根据已知的破坏应力状态，从方程(20)求解得到参数k为

(23)

另一方面，在岩石三轴压缩实验时可以同时测试记录试样的变形情况，获得其体积应力-应变曲线。体积应变的最大值点标示了试样的极限储能状态。它所对应的割线模量K近似了岩石的弹性体积模量，且有

3K=(σV)p/(σV)p

(24)

这里，(σV)p和(εV)p分别表示体积应力-应变曲线上应变最大值点的体积应力和体积应变值。若单轴压缩时二者的取值分别为(σV)0和(εV)0，且剪切弹性模量为常数，由式(6)，得

(25)

因此，参数k也可以通过体积应力-应变曲线峰值点的坐标值计算确定。

3.2 临界能量条件的适用性验证

从上文分析看出，参数k可以根据破坏发生的应力状态从临界能量条件计算确定，也可以根据材料体积应力-应变曲线的体积压缩峰值点坐标进行估值。如果两者一致，正好说明临界能量条件的正确性。因此，临界能量条件适用性可以通过参数k的这种一致性进行验证。

文献[26]给出了Fauske大理岩在侧限压力σ1=σ3分别为0、10、30、55、85和120MPa时，每组三个试样的平均压缩强度，见表1。Fauske大理岩的单轴压缩强度为σC= 93.2MPa，破裂角为θC= 66°[26]。从式(21)计算得到，参数k0= 0.3346。根据临界能量条件的解答式(23)，计算得到不同侧限压力下的参数k值，记为(k)E。同时给出了参数k值的误差δk=|(k)E-(k)ε|/ (k)E×100%，见表1。

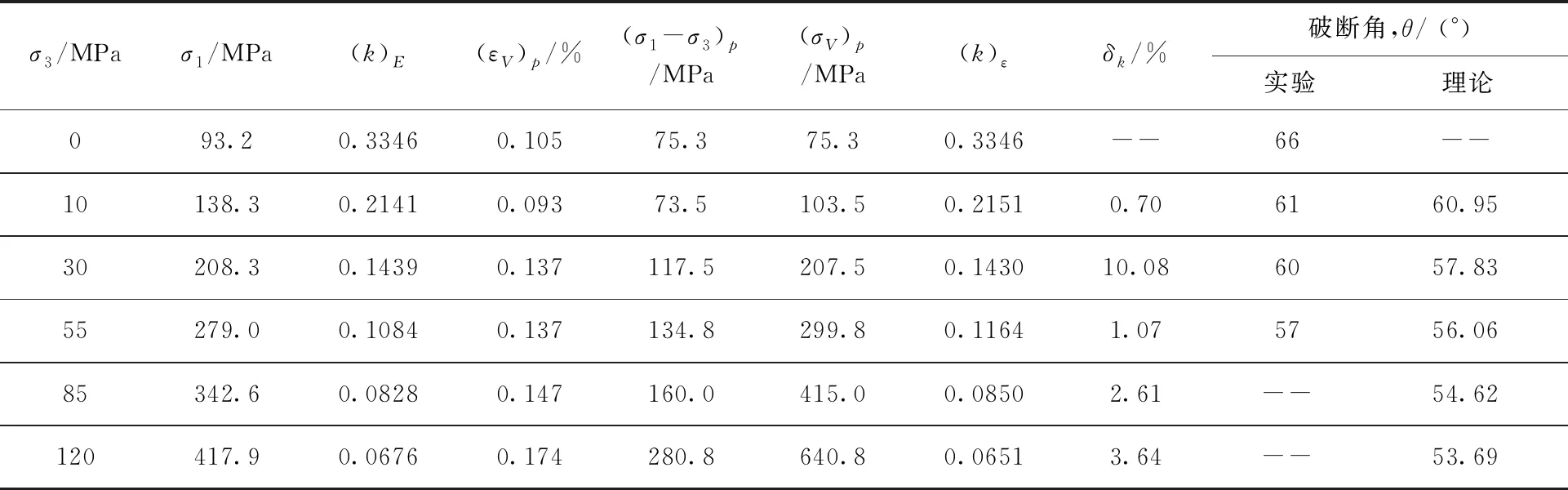
表1 Fauske大理岩的实验结果及临界能量条件的验证计算

在不同侧限压力下，Fauske大理岩的压缩差应力σ1-σ3随轴向应变εA及径向应变εR的变化曲线如图1所示。相关曲线是文献[25]所给实验记录在峰值强度前代表性离散点的三次函数拟合插值结果。实验所用的是圆柱试样，体积应变可以近似为εV=εA+2εR，由此得到图2所示压缩差应力 (σ1-σ3)的体积应变εV变化曲线。图中同时标示了体积应变最大值点的坐标值((εV)p,(σ1-σ3)p)。根据体积应变的最大值(εV)p及其所对应的体积应力(σV)p，利用式(25)计算得到不同侧限压力条件下参数k的值，记为(k)ε，如表1所示。

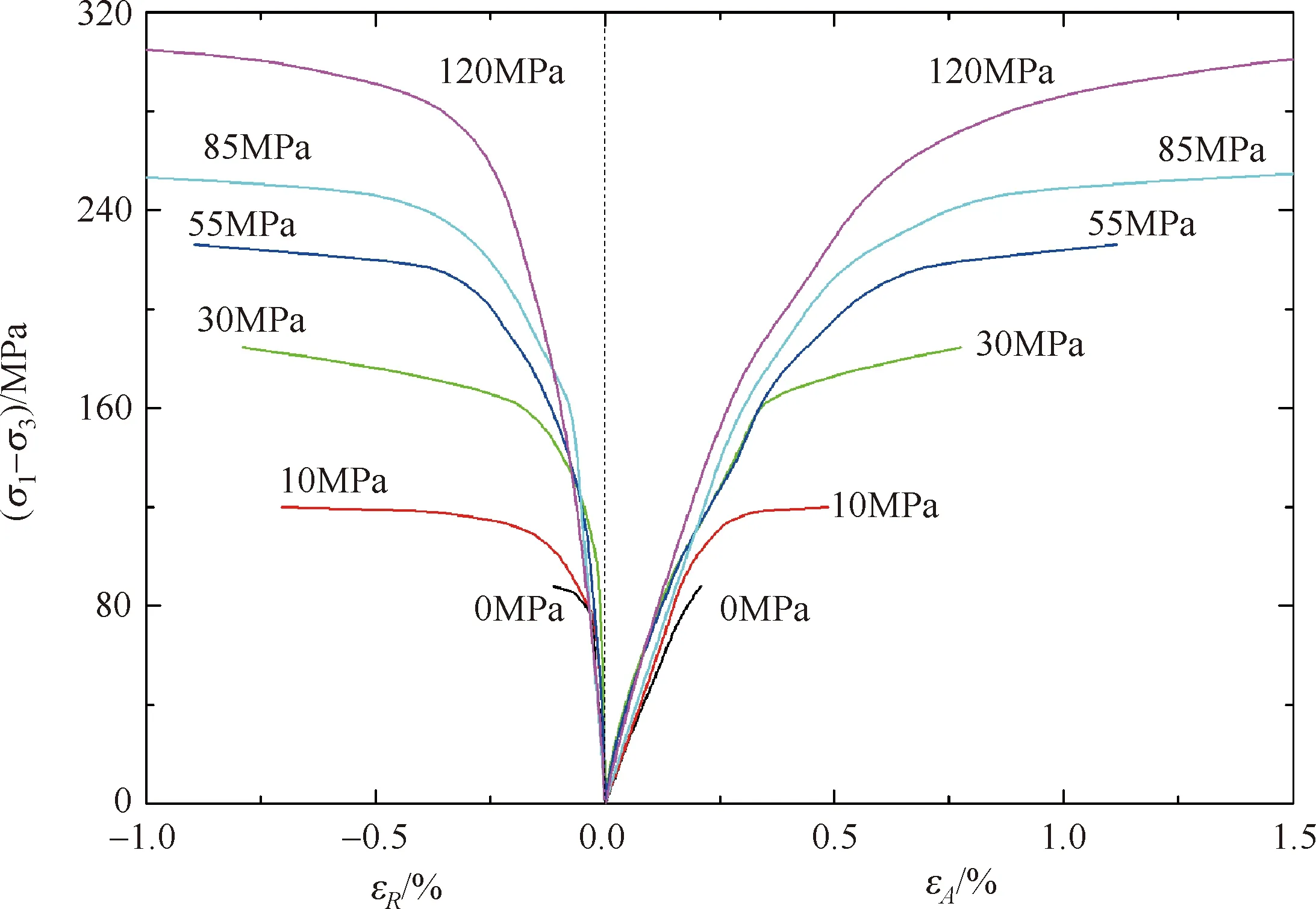
图1 Fauske大理岩三轴压缩差应力-应变曲线

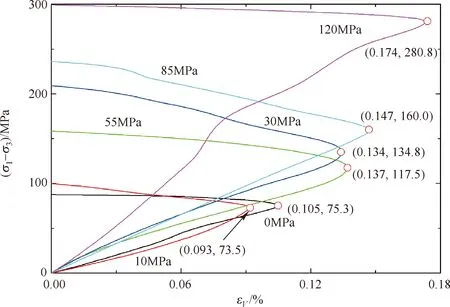
图2 Fauske大理岩三轴压缩差应力-体积应变曲线

从表1可以看出，上述两种方法所获得参数k的最大相对百分误差为10.08%，表明了二者良好的一致性。由此可见，临界能量条件用于断裂分析的正确性。此外，从破裂位向关系式(10)的第一式，得到破断角θ为

(26)

将实测破坏应力及临界能量条件确定的参数k值(k)E代入上式，计算得到破断角的理论结果如表1所示。可以看出，理论值与实验结果良好的一致性。

与Fauske大理岩分析完全类似地，利用侧限压力0、10、30、55和85MPa时Iddefjord花岗岩的三轴压缩实验结果[26]，如表2所示，可以进行临界能量条件的验证计算。实验表明，Iddefjord花岗岩的单轴压缩强度σC= 129.1MPa，破裂角θC= 79°[26]，从式(21)计算得到参数k0= 0.4636。图3给出了实验曲线插图[26]在峰值强度前代表性离散点三次函数拟合的压缩差应力σ1-σ3关于轴向应变εA和径向应变εR的变化曲线。它们所对应的体积应变曲线如图4所示。

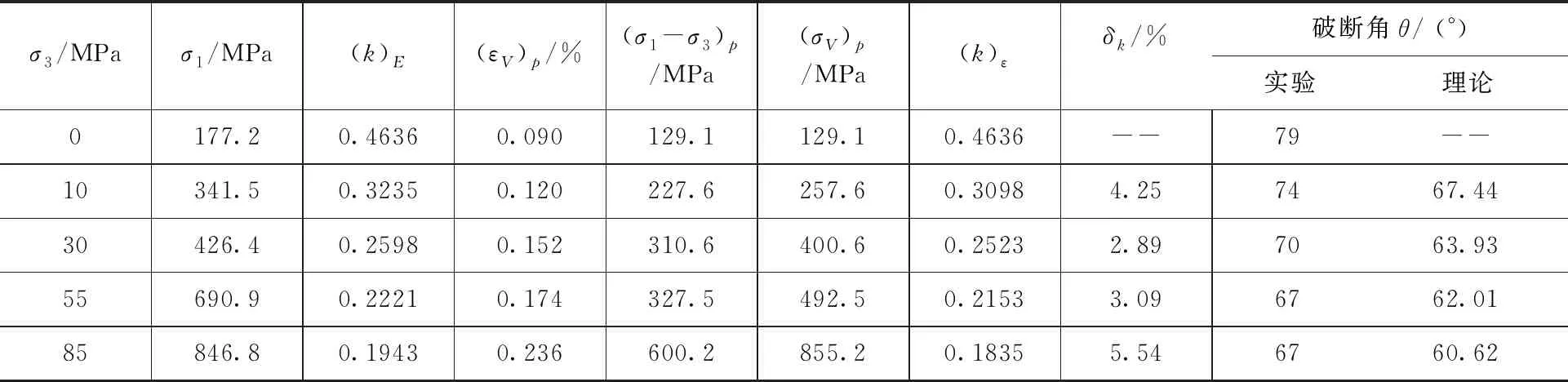
表2 Iddefjord花岗岩的实验结果及临界能量条件的验证计算

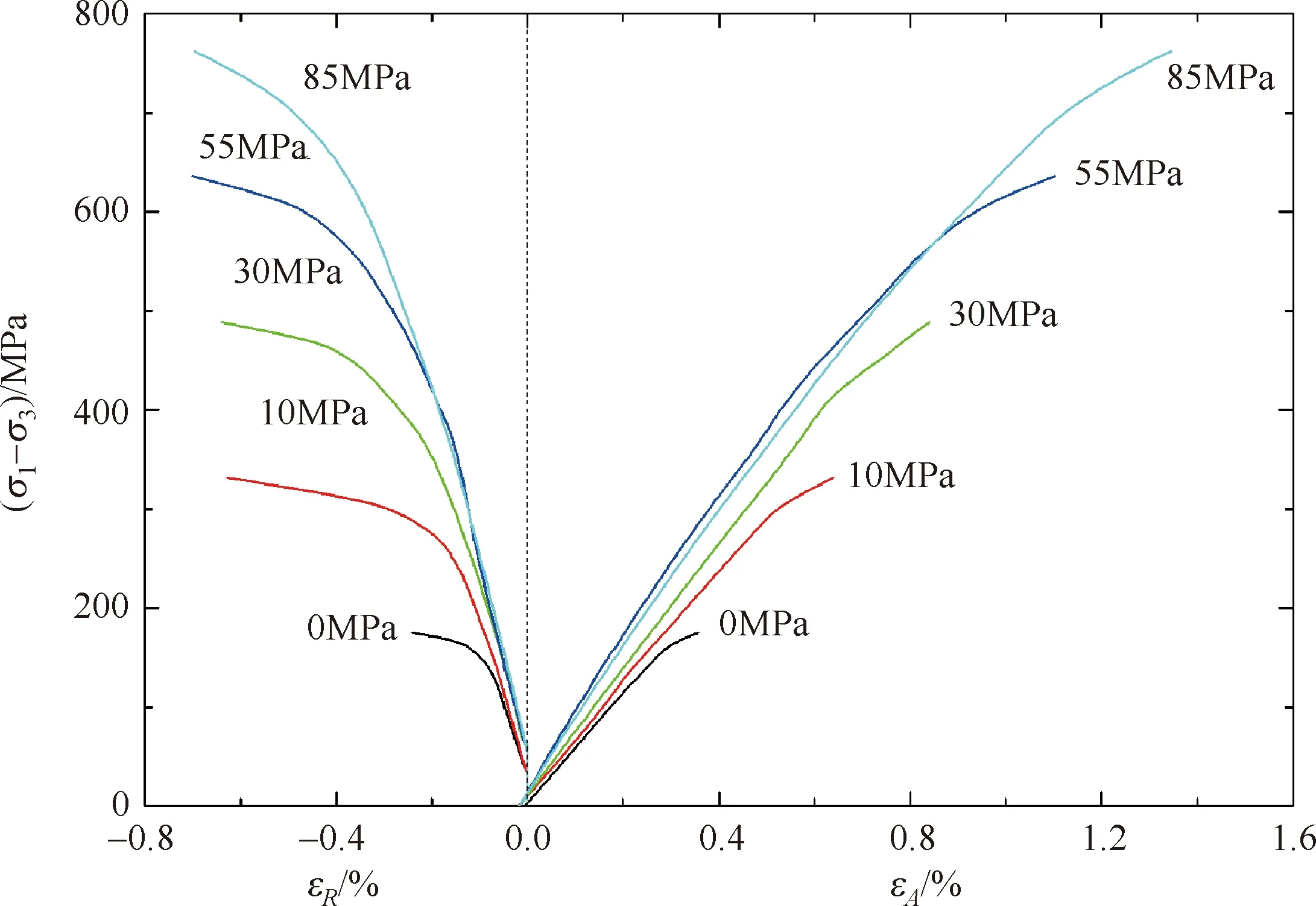
图3 Iddefjord花岗岩三轴压缩差应力-应变曲线

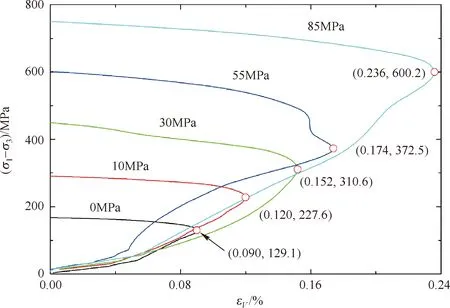
图4 Iddefjord花岗岩三轴压缩差应力—体积应变曲线

从式(23)计算得到Iddefjord花岗岩参数k的值(k)E，从体积应变曲线图4读取的数据结合式(25)，计算得到参数k的值(k)ε，如表2所示。对比可见，两种方法所获得参数k基本一致。不过，破断角的理论与实验值存在着明显的差异。如果注意到试样破裂的原始照片[25]，可以看出，这里的理论结果更接近于真实断裂位向。其实，断裂发生的主导控制破坏面的位向应该非常接近上述理论破坏角。宏观破坏面的形成是这些主导控制破坏面彼此贯通的结果。它比仅仅只关注初始裂纹的影响[22]能更为合理地解释类似花岗岩这类高硬度或高脆性岩石压缩破坏面的翼状裂纹现象[27]。

3.3 临界能量条件的基本特征

临界能量条件(14)为以断裂形式发生的材料破坏现象提供了一个一般性能量描述关系。一旦参数k的变化规律得到确定，这个能量关系将直接转化为材料破坏强度准则。因此，临界能量条件为材料破坏准则的建立提供了理论基础。

不同于Griffith断裂理论[13]，断裂临界能量条件仅关注破裂释放能量的大小，并不直接描述材料所储存弹性能随裂纹发展或断裂形成的释放过程。与介质力学基本方程的联合分析，应该有合适的理论解答用于表征断裂发生或裂纹扩展时外力作用能量耗散演化关系。断裂力学已经建立了成熟的理论体系，通过裂纹-材料系统总能量变化揭示了能量耗散规律。其中，初始裂纹被作为力学模型的构成要素。如果不考虑初始裂纹或者几何奇异性，理论模型失去了初始裂纹的支撑性要素，材料破坏强度准则该如何合理表述？与此相对应，材料力学给出了四个强度理论。稍作分析，不难发现，第一和第二强度理论属于实验现象的经验总结，第三和第四强度理论有合理物理解释，却没有考虑到破坏面上正应力的影响。可以看出，断裂临界能量条件的概念弥补了这一不足。因此，它也构成了忽略初始裂纹影响条件下断裂力学理论能量分析的某种补充。

临界能量条件注意到断裂面上载荷卸除所引起弹性能的释放并转化为裂纹表面能的事实。它以纯剪破坏作为参考状态，通过裂纹表面能的纽带作用并有效地延伸，指明了不同应力状态下断裂能之间的联系，从理论上严格证明了材料强度判据的基本构想，即依据简单应力状态的试验结果可以推知复杂应力状态下材料的强度特性。

4 结论

(1) 对于那些不存在或者不考虑初始裂纹和几何奇异性的材料，断裂力学理论还没有明确的强度分析处理方法。因此，本文放弃了初始裂纹这个断裂理论模型基本要素，将考察对象退化到物质点，在能量耗散关系基础上，提出一个断裂发生的临界能量条件。

(2) 断裂面上一点的断裂能包含剪切能和体积能两个部分。前者是该点的切应力关于弹性切应变的势能，后者是正应力关于体积应变在两个方向同时作用的变形势能。该能量的最大值确定了真实断裂能，它所在平面的方向限定了断裂发生的位向。真实断裂能转化为新生裂纹表面能的能量守恒关系，给出了断裂的临界能量条件。

(3) 断裂临界能量条件包括了两个材料参数：材料的纯剪强度；剪切弹性模量与体积模量比值相关的随应力状态变化的可变材料参数。后者可以由断裂发生的应力状态计算确定，也可以依据其定义式在弹性剪切模量常数近似条件下由体积应变的极限状态值计算确定。两种方法所得结果的一致性给出了临界能量条件实验验证的技术途径。应用Fauske大理岩和Iddefjord花岗岩三轴压缩实验结果的分析计算结果表明了临界能量条件的正确性。此外，破断角的理论值与实验结果良好的一致性进一步证实了理论分析结果的正确性。