动手做 抓本质 促思维
2020-09-15李丽
李丽

【摘 要】 数学学习的重要目标就是促进思维的发展。数学思维的关键是进一步对数学对象的本质和规律加以认识,而小学生的数学学习一般是从观察和操作等直观活动开始的。
【关键词】 动手操作;本质;思维
数学家陈省身先生曾经说过:数学是好玩的。而直指数学本质的直接体验则会成为学生学会、乐学的通幽捷径,帮助学生展开有效的思維活动。下面,笔者就“动手操作,直接体验,迸发学生思维”方面结合几个案例片段进行分析。
一、紧抓本质动手做
【案例一】《圆的认识》(强震球)
(一)导入——感悟圆的科学概念。
(二)画圆——丰富表象,突出本质。
1.圆规画圆。
(1)交流画圆的方法。
(2)尝试画圆。
(3)规范画圆。
2.场地画圆。
3.钉绳画圆。
4.沟通联系,突出本质。
(三)内化——认识圆各部分名称,自主理解特征。
1.认识圆心、半径、直径。
2.解决问题,内化特征。
强老师先让学生尝试用圆规画圆,再利用视频演示规范画法,并再次尝试画圆。在看似潦草的教学过程后,强老师要求学生讨论如何在操场上画一个圆,从而抛弃圆规,利用绳子及其他工具合作画圆,初步理解画圆的本质:“定点(圆心)”“定长(半径)”“旋转一周”。师生比赛钉绳画圆(学生用的皮筋会伸缩,教师用的普通绳子可以定长),则在游戏中发现画圆的本质:绳子的长度不能变,也就是圆规两脚尖的距离不能变,由此引出:点、定长、旋转一周。
整个过程,基于圆的本质“圆是到定点(圆心)的距离等于定长(半径)的点的集合”展开教学,将学生置身于发现者、探索者的角色中,在画圆为主线的操作活动中,从本质上认识了圆,学生的思维也在层层递进中得到了深入发展。
二、凸显本质来操作
【案例二】《射线、直线和角的认识》(笔者)
(一)认识两点间的距离。
1.回顾线段特点。
2.两点间的距离。
(二)认识射线、直线。
1.初步感知射线、直线。
激光直观演示射线(一端射出)、直线(两端射出)。
2.操作改画射线、直线。
①你能将下面的线段改画成一条射线吗?射线有什么特点?
②你能将下面的线段改画成一条直线吗?直线有什么特点?
③同桌交流自己的发现。
3.集体交流,认识射线、直线。
4.闭上眼睛感悟射线、直线。
5.动手画一画线段、射线和直线。
……
射线、直线的概念理解具有高度的抽象性。受学生思维水平的限制很难描述,往往是通过打比方或者直接画出来,从而建立概念。鉴于“无限延长”的抽象性,笔者安排了操作演示活动来突破这个难点。在画出射线和直线后,让学生动手操作,把一条线段改画成射线和直线,这个改画的过程看似无用,实则意义深刻,在观察激光笔一端射出激光,射向窗外形成射线,两端射出光线形成直线,初步感知射线和直线后,让学生改画,孩子们想办法,把一个端点擦去,变成射线,把两个端点擦去,变成直线,有的甚至擦去端点后再进行延长。这个一擦一画的过程,凸显了射线、直线概念的本质特征——射线一端可以无限延长,直线则是两端可以无限延长。学生在这个操作过程中思维已经有了更深一步的发展,再在教师的引领下找特点,交流补充归纳,体会射线和直线都可以无限延长,是无法测量的,并通过课件的动态演示,让学生从本质上感知和理解“无限延长”,闭上眼睛想一想线段是怎样的,射线和直线又是怎样的……这样由直观到抽象,由现象到本质,一步一步深化对射线、直线概念的理解。
三、强化本质促思维
【案例三】《认识几分之一》(王晓)
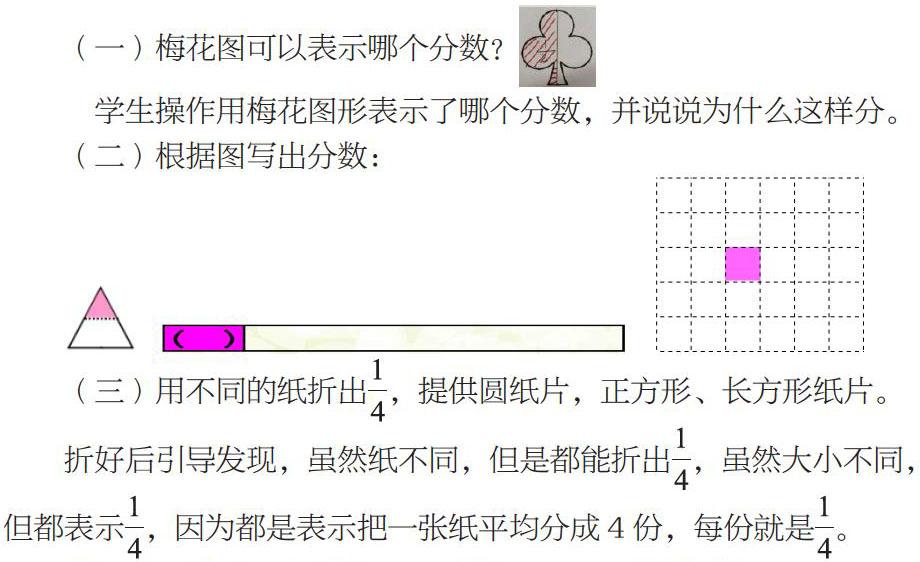
(一)梅花图可以表示哪个分数?
学生操作用梅花图形表示了哪个分数,并说说为什么这样分。
(二)根据图写出分数:
(三)用不同的纸折出,提供圆纸片,正方形、长方形纸片。
折好后引导发现,虽然纸不同,但是都能折出,虽然大小不同,但都表示,因为都是表示把一张纸平均分成4份,每份就是。
分数的关键就是要理解“平均分”。在以往的教学中,我们经常会发现一节课下来,教师反复强调“平均分”这三个字,但学生就是会忘记这最关键的三个字,其实是孩子们分的经验过少。为了强化“平均分”,王老师通过“半具象”的图示,让学生再次分一分,从而强化“平均分”,凸显本质。操作(一)中,学生在梅花图上表示分数时,很自然地想到要把梅花图平均分,再表示出一份,就能找到分数。操作(二)中更是提供了丰富的直观模型,加深了学生对“平均分”的深入理解,这样的练习更能强化对本质的理解,就如三角图,很多学生想到要在图中再分一分,添几条线,使三角形平均分,直条图亦是如此,并且还培养了孩子们的估计能力。操作(三),折一折、比一比、辨一辨:为什么纸不同,却都能表示出?又为什么大小不同,但都是?由此更深一步地内化分数概念的本质:把某个事物平均分成几份,表示这样的1份的数,就是几分之一。
整个操作过程,突出了“平均分”,让学生积累“平均分”的经验,开展多次动手实践的数学活动,多层次、多角度地丰富学生对分数的理解认识。在整个学习过程中,学生不仅掌握了知识,而且发展了思维,学会了探索的方法。
苏教版的数学课堂中,动手操作已然是一个亮点,把主动权交给孩子,带领孩子们真正动起来,让他们充分地经历体验、充分地进行思考,用数学的思维分析,让思维不断生长……
