基于多MEMS传感器组合姿态解算仿真研究
2020-09-15吉寒冬姜文刚
吉寒冬,姜文刚
(江苏科技大学电子信息学院,江苏镇江 212003)
0 引言
近年来,微机电系统(MESM)惯性传感器以及计算机技术快速发展[1],由于MEMS传感器体积小、功耗低、成本低,被广泛运用于航海、机器人以及无人机等领域。但由于传感器本身精度低,陀螺仪长时间会产生累积误差,发生漂移,同时会受到载体运动加速度和磁场环境等因素影响,导致姿态角解算精度低、稳定性差。
为了解决上述问题,陈湾湾使用十二位置标定法,标定MIMU加速度计和陀螺仪的零偏稳定性和安装误差角,对加速度计和陀螺仪的输出值进行补偿,提高姿态角解算精度[2];魏志方利用时间序列自回归滑动平均模型分析方法对原始角速度进行误差建模,通过卡尔曼滤波算法进行误差补偿[3];李景辉采用PI和互补滤波算法,抑制陀螺仪漂移,提高角速度精度[4];Z. X. Hu将拓展卡尔曼滤波应用于传感器姿态解算和漂移补偿[5];黄洋使用多组传感器进行数据采集,运用模糊和PI组合算法对数据进行调节,采用互补滤波与EKF算法分别对误差进行补偿,对姿态数据进行去噪以及预测估计[6];Y. L. Wang研究了利用GPS与MEMS传感器的组合定姿算法[7];孟秀云改进自适应扩展卡尔曼滤波算法,解决传统自适应扩展卡尔曼(AEKF)滤波发散问题[8]。
文中提出一种基于多MEMS传感器组合姿态解算方法。采用12组MEMS传感器,两两对角安装在载体坐标系各轴上,使用两组模糊和两组PI算法对测量模块的测量值与观测值之间的向量积进行调节;利用互补滤波对角速度进行误差补偿,抑制陀螺仪漂移,最后通过自适应扩展卡尔曼滤波对姿态进行预测估计,求得精确的姿态角数据。
1 初始姿态角模型
设地理坐标系为xeyeze东北地方向,载体坐标系xbybzb,空间关系如下:
(1)


(2)
(3)
(4)
(5)
由于MEMS传感器本身工艺的局限性,导致其精度低,陀螺仪漂移,加之外部环境的随机干扰,MEMS惯性传感器中各微传感器模块之间存在耦合误差,因此传统方法已经难以满足实际需求。所以提出一种多MEMS组合传感器姿态解算算法方法,来进行姿态解算求解。
2 数据信息融合
2.1 算法的总体结构
载体坐标系各轴上两两对角安装4组传感器,将采集的数据与四元数估计数据的向量积,通过两组模糊和两组PI算法组合调节,互补滤波调节角速度,利用AEKF对姿态进行预测估计,进而转化为高精度姿态角。姿态解算总体结构图如图1所示。
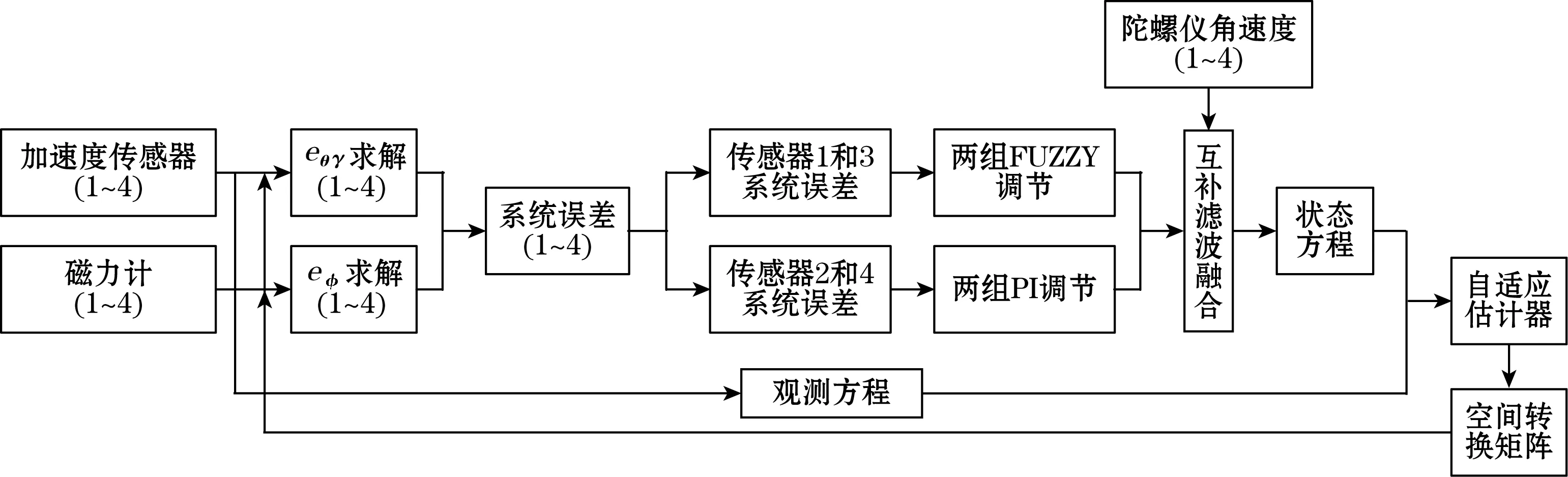
图1 姿态解算总体结构图
传感器安装的优点:减小传感器内部的耦合误差;确保系统可靠性;利用模糊算法的快速性和PI算法的准确性调节数据偏差,互补滤波可以抑制角速度漂移,减小角速度误差,利用AEKF抑制噪声,通过迭代估计提高姿态角数据。
2.2 多传感器信息融合
当载体静止或匀速运动,MEMS传感器中加速度计测量值与空间变换矩阵之间的关系:
(6)
(7)
其中加速计1和加速计2对角安装。Δax、Δay、Δaz为加速度计的测量噪声,通过式(6)和式(7)之间的关系可求得第1组对角安装的θ1和γ1。
(8)
(9)
由于参考坐标系选择东北地,东向磁场近似为0,可以求得φ1:
(10)
同理可得第2组对角安装传感器的姿态角数据如下:
(11)
(12)
(13)
由上式可得系统的姿态角分别为:
θ=(θ1+θ2)/2
(14)
γ=(γ1+γ2)/2
(15)
φ=(φ1+φ2)/2
(16)
Δmx、Δmy、Δmz为磁力计测量噪声,传感器组合安装能够减小内部各微传感器之间的耦合误差。
2.3 角速度调节
在研究中发现,加速度计和磁力计动态响应差,静态响应好,在姿态解算中不会产生累积误差,而陀螺仪在进行姿态解算时,会产生累积误差,但动态响应良好,根据它们在频域上有互补特性,采用互补滤波融合所测得的数据[9],提高系统的稳定性。互补滤波可变换得:
(17)
转换成时域为
(18)

当载体为低速运动时,采用向量积法求得各误差量,即:
(19)
(20)
式中:eθφ、eφ为加速度计和磁力计的测量数据与四元数观测数据的向量积运算;ha和hm为在载体坐标系下加速度和磁力单位向量。
通过模糊算法对传感器1和传感器3陀螺仪输出角速度进行调节,误差e1和e3与其在采样周期内的积分为输入量,u1和u3为输出量,得:
(21)
(22)
传感器2和传感器4由PI控制器对其进行调节,误差e2和e4作为输入量,u2和u4作为PI控制器的输出量,得:
(23)
(24)
(25)
(26)
载体的角速度可由均值得到:
(27)
设定截止频率fc=15 Hz,k为0.8,kp、ki取值为1.5、0.03。
2.4 自适应扩展卡尔曼滤波姿态解算
自适应扩展卡尔曼滤波能抑制噪声[10],对非线性系统具有较好的估计与修正作用,迭代估计提高姿态角精度,具体滤波算法如下:
预测计算:
Xk,k-1=Φk,k-1Xk-1+Γk-1Wk-1
(28)
Zk=HXk+vk
(29)
卡尔曼量测更新校正计算:
Kk=Pk,k-1HT(HPk,k-1HT+Rk)-1
(30)
ek=Zk-HXk,k-1-rk
(31)
Xk=Xk,k-1+Kkek
(32)
(33)
Pk=(I-KkHk)Pk,k-1
(34)
自适应估计器:
Wk=(1-dk-1)Wk-1+dk-1Gk(Xk-Φk,k-1Xk-1)
(35)
(36)
(37)
rk=(1-dk-1)rk-1+dk-1(Zk-HkXk,k-1)
(38)
(39)
(40)
式中:Φk,k-1为tk-1到tk的一步转移矩阵;Γk-1为系统噪声驱动矩阵;ek为残差;Hk为量测矩阵;Wk近似为白噪声;Qk为系统噪声协方差矩阵;Rk为量测噪声协方差矩阵。
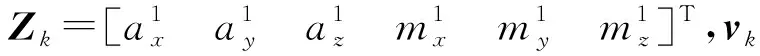
3 仿真验证
为了验证所提出的方法,在MATLAB中设载体坐标系各轴采用4组传感器两两对角安装,设定加速度传感器的随机误差为1×10-4g(g表示重力加速度),磁阻尼传感器的随机误差为50 nT,静态测量陀螺仪随机误差为1/900°/h,MEMS传感器内部各微传感器之间误差相互独立,互不干扰,采用二维模糊控制器,模糊调节器设定误差、误差变化率和输出量的论域分别为[-6,6]、[-6,6]、[-3,3],模糊集均为{NB,NM,NS,ZO,PS,PM,PB},模糊推理语句为If A and B then C;模糊规则表根据专家经验设计;选用三角形隶属函数trimf(x,[a,b,c]);选择Mamdani模糊系统进行推理;反模糊化选用面积重心法centroid。设定自适应扩展卡尔曼滤波中各协方差矩阵初始值为Q0=0.000 1I3×3,P0=0.001I4×4,R0=0.001I6×6,分别在静态和动态两种情况下对传统姿态角解算以及所提方法姿态角解算进行仿真数据分析,在静态时理想状态下,各姿态角应都为0。静态仿真结果如图2~图4所示。静态姿态角误差参数分析见表1。

图2 静态无调节姿态误差

图3 静态PI调节姿态误差

图4 静态模糊和PI组合调节以及本文所提方法姿态误差

表1 静态姿态角误差参数分析 (°)
在动态调节情况下,设定俯仰角θ由0°匀速变化为90°,陀螺仪的随机误差增加到1/400°/h,动态仿真图如图5所示。

图5 俯仰角变化曲线
图5为俯仰角变化曲线,θ从0°匀速变化为90°,从图中可以看出俯仰角变化过程波动非常小,有微小误差,曲线的整体变化趋于真实曲线。
动态情况下仿真对比姿态角误差如图6~图8所示,姿态误差参数见表2。

图6 动态无调节误差
通过表1~表2可得,MEMS传感器在无调节时,误差很大,尤其在动态的情况下,通过数据可以看出陀螺仪漂移大,稳定性低;当加入了PI调节,误差得到抑制,数据波动减小,姿态角精度得到提高,稳定性也得到提高;而通过模糊和PI组合调节,系统误差进一步减小;而文中所提的方法:采用多组MEMS传感器组合采集数据,通过两组模糊和两组PI进行组合调节,互补滤波与自适应扩展卡尔曼滤波组合对角速度进行补偿,系统误差更进一步减小,尤其在动态情况下,模拟俯仰角由0°匀速变化为90°,可以从动态图看出,曲线变化接近真实曲线,从图8可以得出,所提出的方法,稳定性更好,通过以上数据分析对比更能凸显出文中所提出方法的优越性和先进性,更能满足实际需求。
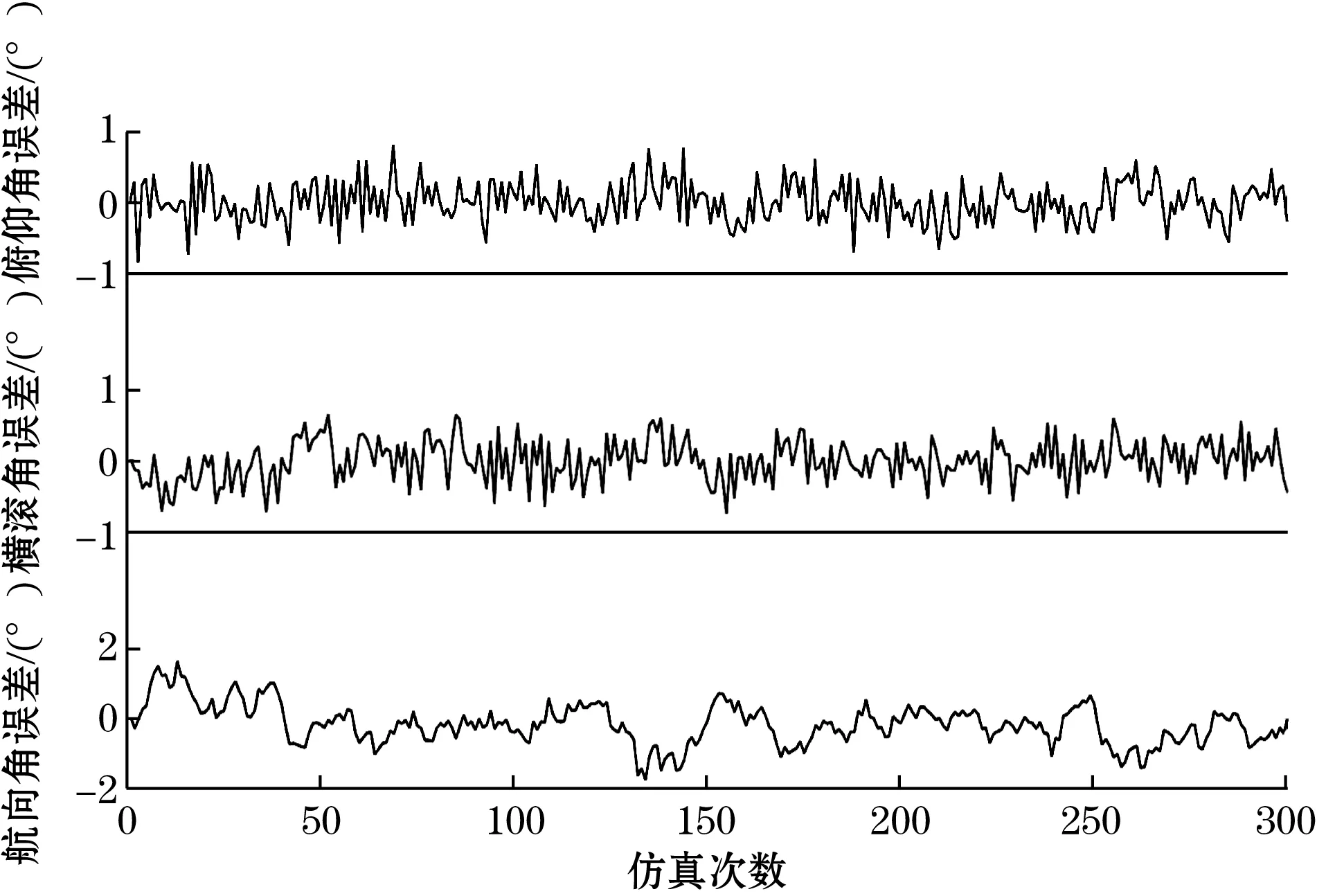
图7 PI调节动态姿态误差

表2 动态姿态角误差参数分析 (°)
4 结束语
文中对传统MEMS传感器姿态解算所存在的问题进行分析,并提出一种多MEMS组合传感器姿态解算方法,具体步骤如下:
(1)在载体坐标系各轴上分别采用4组传感器两两对角安装,多传感器组合安装的优点:能够减小各惯性模块之间的耦合误差问题;提高系统的可靠性;提高输入、输出信息可信度。
(2)采用两组模糊和两组PI算法组合调节,相较于使用单PI调节,更加精准,而采用互补滤波可以抑制角速度漂移。
(3)利用自适应扩展卡尔曼滤波一方面能够对姿态角进行预测估计,更新四元数微分方程,提高姿态角精度,另一方面能够减弱PI算法和互补滤波算法相结合可能导致的超调和振荡问题。
后续需要针对自适应扩展卡尔曼滤波所存在的问题进行进一步研究。这些问题包括公式矩阵较多,计算量较大;系统噪声协方差与量测噪声协方差同时更新会引起滤波发散;系统中仍存在超调和振荡等。
