轴套外径对螺栓连接压缩变形量的影响及理论优化

2020-09-14车承牮阳光武肖守讷朱涛杨冰柯新

铁道科学与工程学报 2020年8期

车承牮，阳光武，肖守讷，朱涛，杨冰，柯新

车承牮，阳光武，肖守讷，朱涛，杨冰，柯新

(西南交通大学牵引动力国家重点实验室，四川成都 610031)

对于含轴套的同轴紧固及同轴受载的螺栓连接结构，夹紧区域内压缩变形体形状会影响螺栓连接结构轴向压缩变形量的理论计算。通过采取仿真与理论多项式计算对比，发现轴套下方的压缩变形体继续扩散。当轴套外径较大时，轴套下方的变形体起始直径为轴套外径，5个模型变形体压缩变形量的理论模相对误差的最大值为7.07%。考虑到工程中螺栓连接结构可能会出现种类繁多的情况，对轴套外径较大的螺栓被连接件的压缩变形体形状优化，提出体积影响因子与应力影响因子，优化后的结果相对误差的最大值为6.95%，在不失去精度的同时简化了计算，具有一定的工程意义。

螺栓连接；轴套；轴向压缩变形量；理论模型优化；有限元方法

由于连接力大、结构紧凑、便于拆卸等优点，螺纹联接广泛存在于各类机械结构中，是最常用的紧固手段之一[1]。螺栓发展的主要时期是在工业革命时期，经过了百年的发展，螺栓在工业领域里成为了一种重要的连接件。VDI2230[2]是德国工程师协会发布的指南，为高强度连接螺栓的理论计算提供参考。此指南被广泛认可及引用。但通过实验及仿真等方法发现指南仍存在不足，并在多处进行了简化。Motosh[3]于1976年提出了计算螺栓轴向压缩量的多项式方法。相比于VDI2230中将压缩变形体各受压层的压应力视为均匀分布，Motosh在算式中将压缩变形体各受压层的压应力作为4次分布考虑。向福腾[4]基于压应力4次分布假设，对压缩变形体可能出现的各种形状其轴向压缩刚度进行了理论与仿真分析。夏冬等[5]对不同尺寸和不同材料的螺栓连接垂向刚度进行研究，提出了当压缩变形体为圆锥体时的更精确的公式。Canyurt等[6]通过有限元分析与遗传算法对螺栓连接刚度进行了预测。在以上学者研究的基础上，对改变螺栓轴套外径情况下，研究其压缩变形体形状与压缩变形量。不同情况下压缩变形体有不同的等效形式，提出了较为精确的影响因子，并对起始直径在这种情况下进行进一步优化。为之后特殊结构的螺栓研究提供参考。

1 理论分析模型

VDI2230中指出螺栓内夹紧区域的压缩变形体可等效为双平头圆锥以及双平头圆锥与圆柱结合的2种情况，这2种情况中圆柱与圆锥的外径都不超过被连接件的边界。但是经过研究发现，与轴套相连的压缩变形体可以继续扩散，不受轴套外径的限制。

轴套的长度为20 mm，于是M12的螺栓的压缩变形体起始直径应修正为支承面外径w的1.4倍，所以当z＜1.4w时，轴套内压缩变形体为空心圆柱，被连接件内压缩变形体为对称的平头圆锥，如图1(b)；当z＞1.4w时，轴套内压缩变形体为空心圆柱与平头圆锥的结合，被连接件内压缩变形体为不对称的平头圆锥，如图1(c)。

1.1 dz＜1.4dw时压缩变形量的理论计算

轴套内压缩变形体的轴向压缩变形量可表示为：

对压缩变形量的计算，第1个等号后的式子通过积分的思想计算总的变形量，为理论计算方式。

第2个等号后的式子为参照VDI2230[2]的5.1.2.1节提到的同轴紧固单螺栓连接被连接件压缩变形量公式，为实际计算方式。

第3个等号后的式子中应力值是通过仿真的方式得到，应力值与弹性模量的比值为应变值，因为螺栓是同心紧固及加载，螺栓应力情况是轴对称的，所以受压层的平均应变即受压层总应变与受压层面积的比与该受压层螺栓孔边缘到受压层边缘这一段平均径向应变即这段距离的总应变与这段距离的比是相同的，平均径向应变可以通过将这段距离上的应变值进行积分再除以这段距离得到，通过对平均径向应变沿进行轴向积分可以得到总的轴向压缩变形量，为仿真计算方式。

被连接件内的压缩变形体为对称的两平头圆锥，圆锥变形体的总高度为b，受压层的横截面积为：

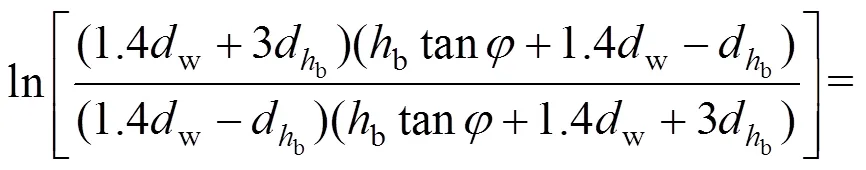
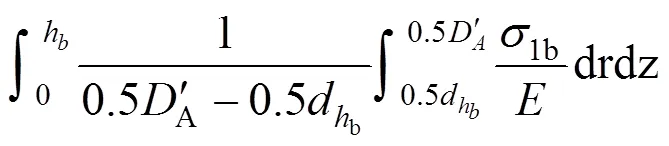
夹紧区域整个压缩变形体的轴向压缩变形量1为1z与1b之和。

圆锥变形体半顶角可由式(6)确定：

1.2 dz＞1.4dw时压缩变形量的理论计算

对于图1(c)中的模型，轴套内压缩变形体为空心圆柱与单平头圆锥的结合，圆锥变形体高度1的计算公式为：

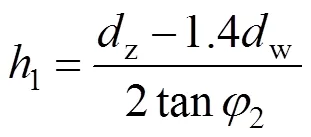
起始外径为1.4w，横截面积为：

被连接件内圆锥变形体半顶角1同样由式(6)确定，轴套内圆锥变形体半顶角2可由式(9)确定：

圆柱变形体高度为2，轴套内压缩变形体的轴向压缩变形量可表示为圆锥变形体变形量与圆柱变形体变形量之和：

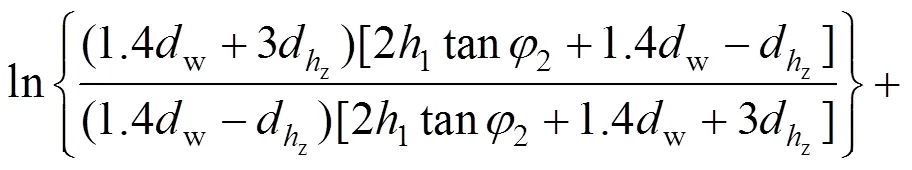
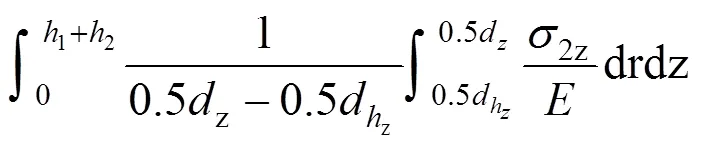
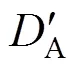
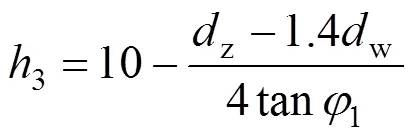
被连接件内压缩变形体的轴向压缩变形量可表示为两圆锥变形体变形量之和：

夹紧区域整个压缩变形体的轴向压缩变形量2为2z与2b之和。

2 有限元分析模型

根据GB/T 97.1—2002[8]和GB/T 848—2002[9]，选取公称直径为M12 mm的高强度螺栓，轴套长度为20 mm，被连接件为2个等高度的圆盘，高度为10 mm，根据不同的轴套外径建立12个螺栓连接有限元模型，尺寸及材料参数如表1与表2所示。

表1 模型基本参数

由文献[10]取k/=0.7，仿真模型采用SOLID 185单元离散，设置预紧力在被连接件接合面处的螺杆上，数值为10 000 N，采用PRETS179单元进行模拟，采用COMBIN14单元对模型施加约束，并进一步采用接触对约束螺栓结构垂直于轴线的位移，接触算法设为增广拉格朗日法，其中ContactⅠ与ContactⅣ摩擦因数为0.12，ContactⅡ与ContactⅢ摩擦因数为0.23。钢材的密度为7 850 kg/m3，弹性模量为206 GPa，泊松比为0.3。图2与图3为仿真模型示意图。

表2 各模型不同参数

图2 仿真模型参数

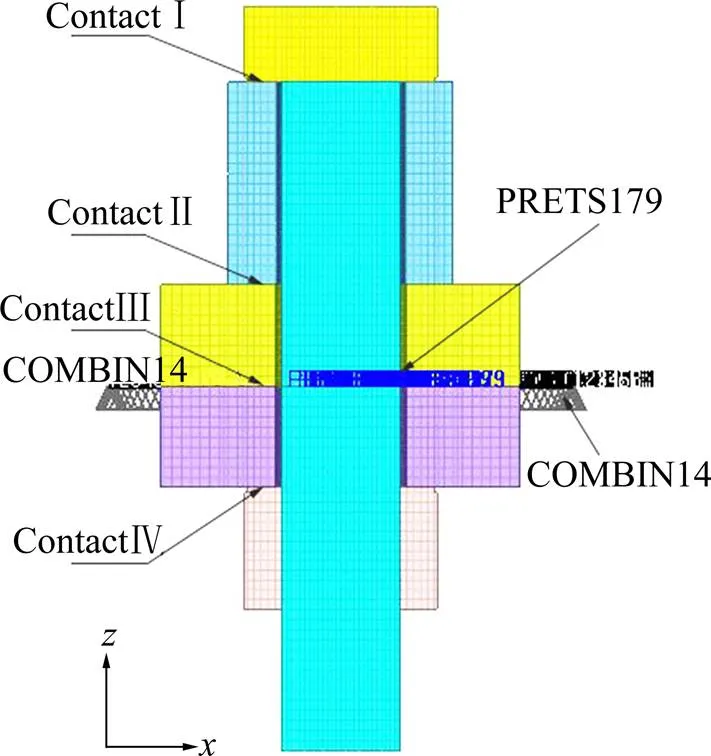
图3 接触对、弹簧及预紧力示意图

3 理论与仿真计算

3.1 模型应力云图

不同轴套外径螺栓连接结构的应力云图类似，此处仅以轴套外径为支承面直径的1.2倍和1.8倍的应力云图作对比，如图4所示。

(a) dz=1.2dw；(b) dz=1.8dw

仿真结果显示：对于图4(a)的螺栓连接结构，被连接件与轴套的过渡处会产生应力集中，但被连接件应力分布受轴套影响不大，轴套内部应力全为压应力；对于图4(b)的螺栓连接结构，被连接件应力明显不根据被连接件结合面对称，压缩变形体在轴套下方继续扩散，轴套内部应力出现拉应力。

3.2 理论计算与有限元计算对比分析

有限元计算中轴套与被连接件的轴向压缩变形量是由每一个受压层的平均应变在轴向进行积分得到。模型与其受力方式全部关于轴对称，所以受压层的平均应变为径向线段平均应变。

在受压范围内提取径向线段各个节点应力值并在径向积分，将得到的结果除以受压范围得到径向线段平均应变。以k为横坐标，轴套径向线段平均应变为纵坐标；l为横坐标，被连接件径向线段平均应变为纵坐标作平均应变曲线图5与图6(a)，6(b)和6(c)分别代表轴套，上被连接件，下被连接件。

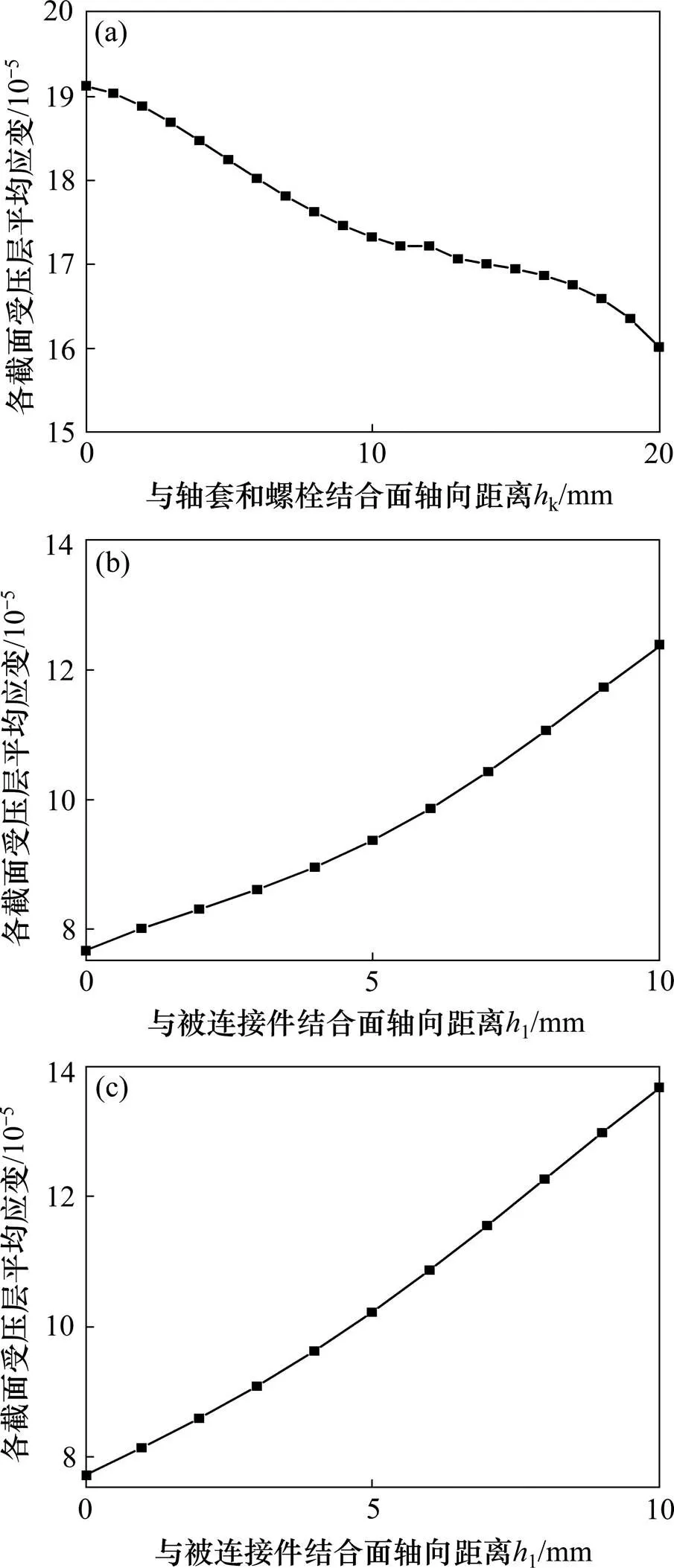
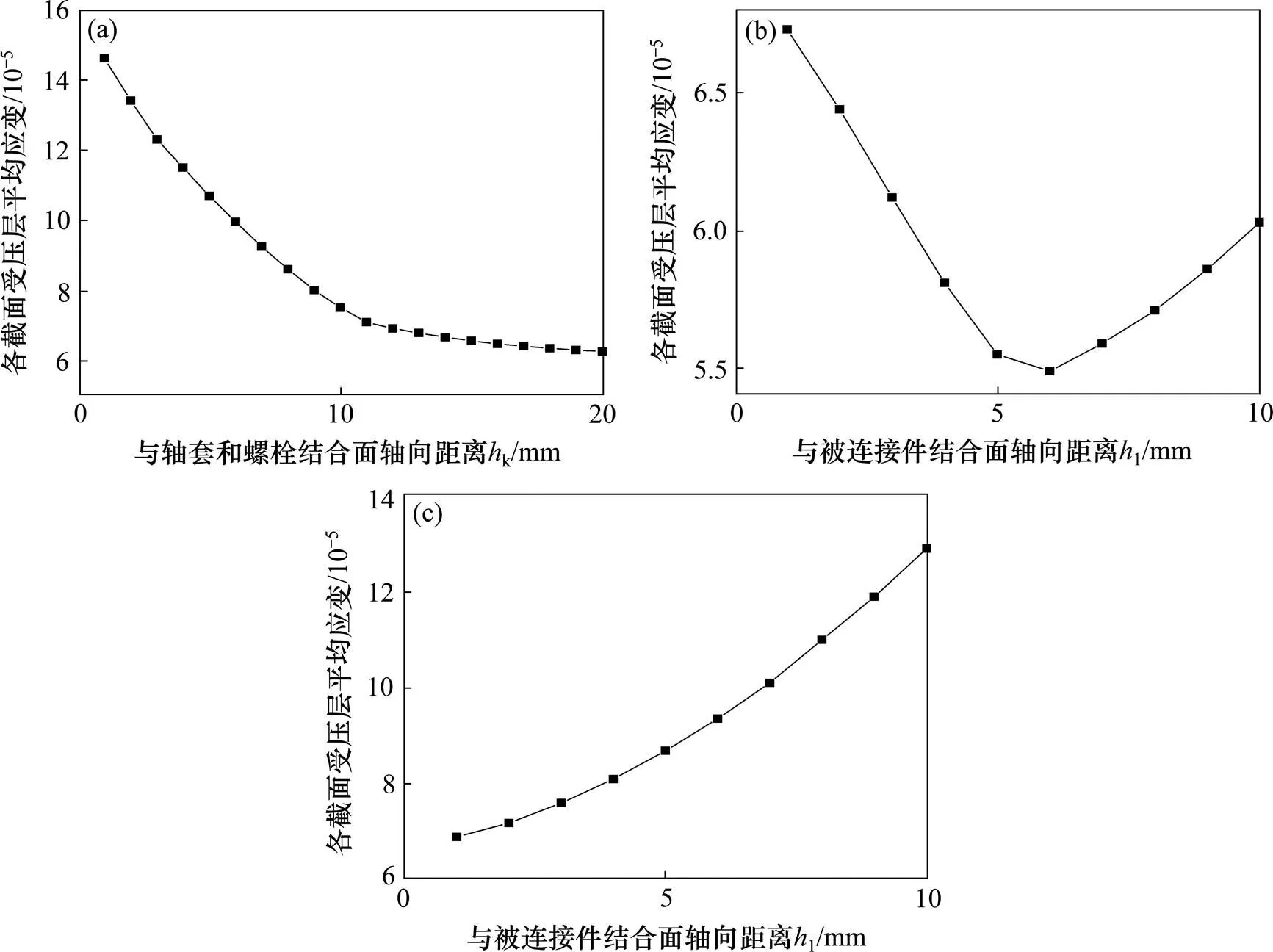
(a) 轴套轴向应变曲线；(b) 上被连接件轴向应变曲线；(c) 下被连接件轴向应变曲线

越靠近螺栓和螺母支承面，受压层的平均应变越大，被连接件受压层的平均应变曲线存在一个拐点，对于z＜1.4w的情况，拐点位于被连接件结合面，对于z＞1.4w的情况，拐点位于被连接件结合面之上。

将轴套与被连接件的受压层的平均应变沿轴向积分，可以分别获得轴套与被连接件的轴向压缩变形量。

利用第1章的公式计算轴套与被连接件的出理论压缩变形量的值与仿真计算的值进行对比分析，二者之间的相对误差计算公式为：

其中：为理论压缩变形量；为仿真压缩变形量；为相对误差。

=1与2分别代表轴套与被连接件的情况。

夹紧区域整个压缩变形体压缩变形量理论计算值与仿真计算值之间的相对误差如表3所示。

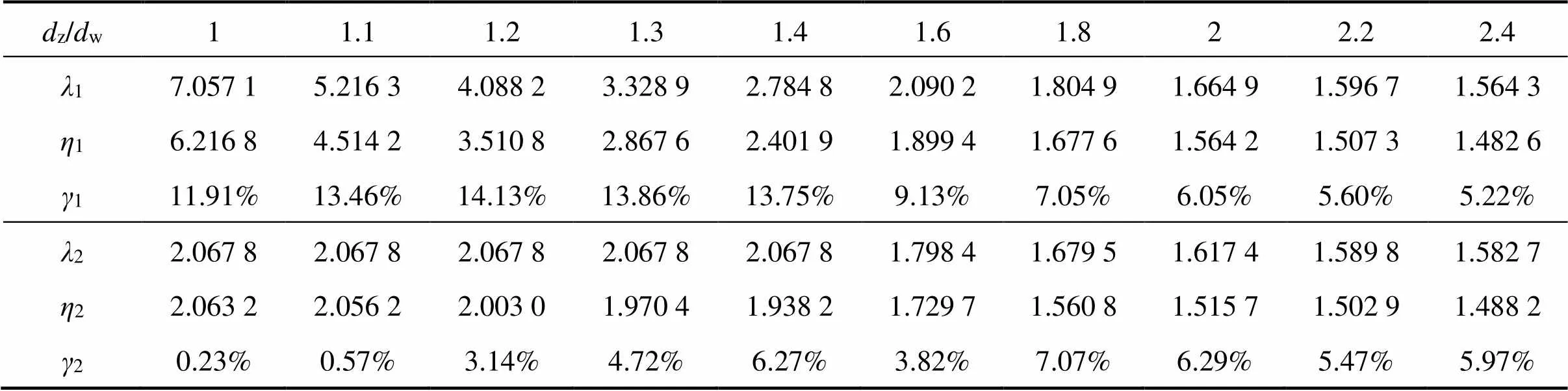
表3 螺栓理论计算与仿真计算压缩变形量与相对误差

从表3中可以看出：当z/w＜1.4时，轴套压缩变形量的相对误差都大于10%，随着轴套外径的增加，轴套压缩变形量的相对误差呈现逐渐减小的趋势；被连接件压缩变形量的相对误差一直很小，但这种计算方法较为繁琐，需要计算2个不同的单平头圆锥变形量。针对这一情况有必要进行优化以满足工程计算的需求。

4 理论计算优化

被连接件的变形量对载荷分配系数影响很大，所以会对螺栓的校核工作产生重大影响。

对于第1章的理论计算公式需要考虑2个不同形状的变形体，不利于计算种类较多且复杂的有轴套的螺栓连接结构，此时可将模型优化为图7。

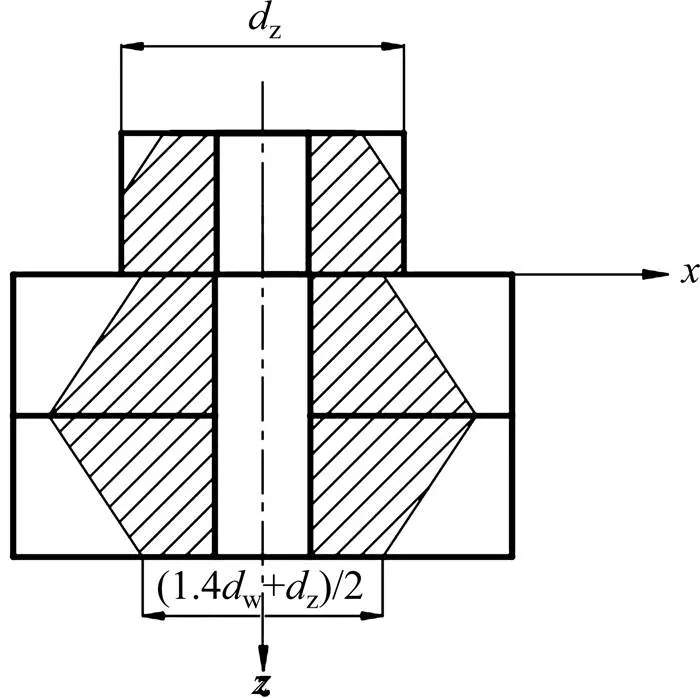
图7 解析模型优化

优化前与优化后压缩变形体体积a与b为：

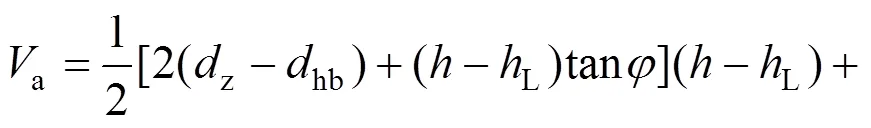
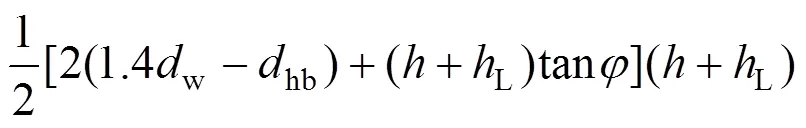
由于：

式(14)比式(15)可得：

为体积优化因子，新的变形体压应力部分减少拉应力部分增多，所以再引入应力优化因子：

式(17)变为：

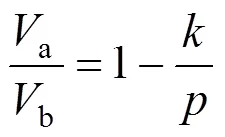
优化后的结果及其相对误差列于表4。

表4 优化理论压缩变形量与相对误差

=3与4分别代表引入与同时引入与的情况。将3种理论计算方式产生的相对误差做成更为直观的直方图，见图8。

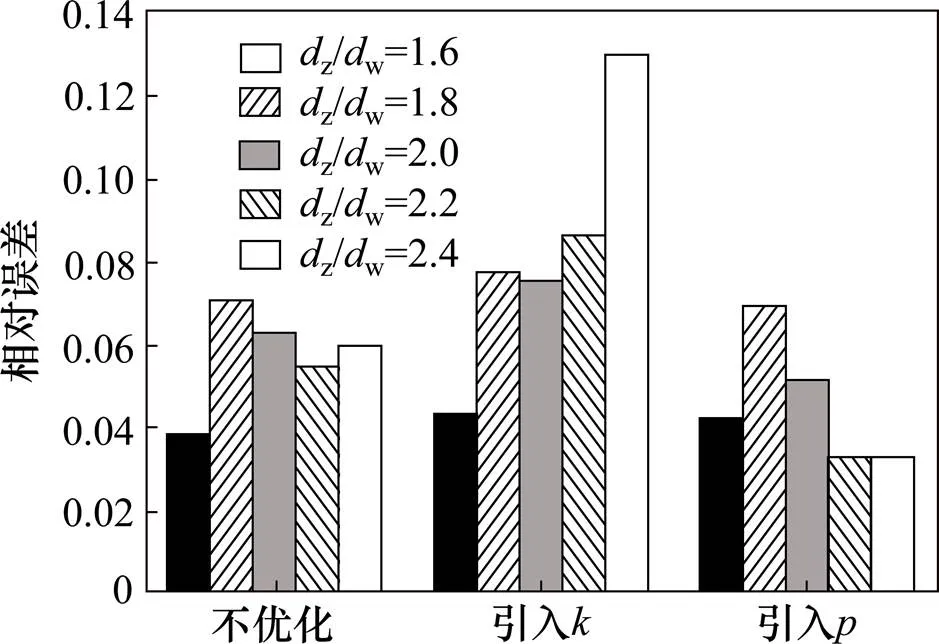
图8 压缩变形量的相对误差直方图

由图8可以看出，原始的计算结果与经过2次修正的计算结果与仿真结果都有良好的对应情况，只经过体积修正的计算结果其相对误差随着轴套外径增大而增大，其误差难以估量。所以事实上，应力优化因子虽然是由于拉压应力分布引入的因子，但考虑的是体积因素，其作用相当于外径较大的情况下，体积优化因子值过大这一情况，对进行缩放。

5 结论

1) 带有轴套的螺栓其压缩变形体在轴套下方继续扩散，z＜1.4w时，轴套和被连接件的压缩变形体形状为圆柱，对称的双平头圆锥；z＞1.4w时，轴套和被连接件的压缩变形体形状为圆柱与单平头圆锥，不对称的双平头圆锥；

2) 应用Motosh的多项式理论按照结论(1)中的压缩变形体形状对轴套及被连接件变形量进行理论计算与仿真计算结果对应情况良好，推出了轴套及被连接件压缩变形量的理论模型，达到了理论与仿真的双向验证；

3) 对z＞1.4w的带有轴套的螺栓进行批量计算时，可将被连接件的压缩变形体优化为对称的双平头圆锥，在引入了体积优化因子与应力优化因子后，其与仿真计算结果对应情况良好，简化了计算。

[1] 侯世远, 廖日东. 螺纹联接松动过程的研究现状与发展趋势[J]. 强度与环境, 2014(2): 39−52. HOU Shiyuan, LIAO Ridong. Research progress on self-loosening of threaded fasteners[J]. Structure & Environment Engineering, 2014(2): 39−52.

[2] VDI 2230 Part 1. Systematic calculation of high duty bolted joints, joints with one cylindrical bolt[M]. Verein Deutscher Ingenieure, 2003: 19−37.

[3] Motosh N. Determination of joint stiffness in bolted connections[J]. Journal of Engineering for Industry, 1976, 98(3): 858.

[4] 向福腾. 螺栓连接件等效压缩刚度计算方法研究[D]. 成都: 西南交通大学, 2016: 15−31. XIANG Futeng. Study on calculation method of equivalent compression stiffness of bolted joints[D]. Chengdu: Southwest Jiaotong University, 2016:15−31.

[5] 夏冬, 阳光武, 向福腾, 等. 压应力非均匀分布下螺栓连接件垂向刚度研究[J]. 机械制造与自动化, 2019, 48(2): 81−84. XIA Dong, YANG Guangwu, XIANG Futeng, et al. Vertical stiffness analysis of bolt fitting under compressive stress non-uniform distribution[J]. Machine Building & Automation, 2019, 48(2): 81−84.

[6] Canyurt Olcay Ersel, Sekercioglu Tezcan. A new approach for calculating the stiffness of bolted connections[J]. Proceedings of the Institution of Mechanical Engineers Part L-Journal of Materials-Design and Applications, 2016, 230(2): 426−435.

[7] 柯新, 阳光武, 夏冬, 等. 螺栓与被连接件间轴向相对刚度的修正计算[J]. 工程设计学报, 2019, 26(1): 45−52, 115. KE Xin, YANG Guangwu, XIA Dong, et al. Modified calculation of axial relative stiffness for bolted joints structures[J]. Chinese Journal of Engineering Design, 2019, 26(1): 45−52, 115.

[8] 铁道科学研究院. GB/T 97.1—2002, 平垫圈[S]. 中国标准出版社, 2002: 1−2. China Academy of Railway Sciences. GB/T 97.1—2002, Plain washers[S]. Standards Press of China, 2002: 1−2.

[9] 铁道科学研究院. GB/T 848—2002, 小垫圈[S]. 中国标准出版社, 2002: 39−40. China Academy of Railway Sciences. GB/T 848—2002, Plain washers-small series[S]. Standards Press of China, 2002: 39−40.

[10] 夏冬. 螺栓连接载荷导入系数问题研究[D]. 成都: 西南交通大学, 2018: 31−36. XIA Dong. Research on load introduction factor of bolted joints[D]. Chengdu: Southwest Jiaotong University, 2018: 31−36.

Influence and theoretical optimization of outer diameter of shaft sleeve on compression deformation of bolt connection

CHE Chengjian, YANG Guangwu, XIAO Shoune, ZHU Tao, YANG Bing, KE Xin

(Southwest Jiaotong University, State Key Laboratory of Traction Power, Chengdu 610031, China)

For the concentric clamping and loading bolt connection structure with the shaft sleeve, different shapes of compression deformation bodies have an effect on the analytical results of axial compression deformation. The equivalent shapes of compression deformation bodies were studied by comparing the simulation with the theoretical polynomial calculation then the compression deformation bodies were found to continue to diffuse below the shaft sleeve. It was found that when the outer diameter of the shaft sleeve was large, the initial diameter of the deformation body below the shaft sleeve was the outer diameter, the maximum relative error of the theoretical solutions of the deformation of the 5 models is 7.07%. However, considering the bolt connection structures might have a wide variety of situations, the shapes of the compression deformation bodies of the clamped pieces when the outer diameter was large were optimized, and the volume influence factorand the stress influence factorwere proposed. The maximum relative error of the optimized results is 6.95% and the calculation is simplified which has certain engineering significance.

bolt connection; shaft sleeve; axial deformation; theoretical model optimization; finite element method