岩石块体系统构建方法及可视化程序开发
2020-09-14张敏思黄思凯高金贺
张敏思, 黄思凯, 杨 勇,2, 高金贺
(1.东华理工大学 土木与建筑工程学院,江西 南昌 330013;2.东北大学 资源与土木工程学院,辽宁 沈阳 110015)
岩体是由许多不同构造、产状和规模的结构面(断层面、节理面、裂隙面等)切割而形成的复杂结构体系。结构面及临空面间相互切割,在岩体内部形成大小不等、形态各异的块体,在一定程度上控制着岩体工程的稳定性。因此,在一定区域内构建符合实际工程的岩石块体系统是一项非常重要的基础性研究。
1985年,块体理论被正式提出(Shi et al.,1985),并用以分析结构面与临空面间形成的块体稳定性。由于块体理论与工程实际紧密结合,自其诞生以来得到了快速发展。块体的构建经历了从贯通结构面到有限结构面,从临空面到全空间的过程。自2000年以来,赤平投影解析法也被提出,并应用于地下硐室岩体稳定性分析(张子新等,2010)。随后,针对拓扑学中的单纯同调理论(Lin et al.,1987),学者从块体形态入手进行了更为深入的研究(Lu,2002)。近些年来,Yu等(2009)通过划分凸体子区继而切割再合并的方法实现块体系统构建。在此基础上,学者又提出更为精细化的块体识别方法(Zhang et al.,2012;张敏思等,2016,2017)。为了解决曲面结构面下的空间切割问题,三角单元网表达空间曲面被采用,并对块体进行切割(Zheng et al.,2015)。目前为止,众多学者都针对块体系统的构建提出了不同方法,但少有文献给出详细算法及具体实现过程。
笔者结合前期研究工作(张敏思等,2016,2017;梁恩云等,2016;宋凯等,2017),以平面对多面体切割算法为基础(Yu et al.,2009),开发一套非贯通结构面切割下岩石块体系统构建方法,并给出关键技术及具体算法实现过程。采用VC++中MFC进行可视化程序开发,选取实际工程对所开发程序进行验证。
1 基本原理
图1为岩石块体系统构建流程图。首先,对工程岩体模型进行网格的划分,将划分的单元块体数据记录下来。向模型中继续添加导入的结构面信息,判断出能与结构面相交的单元块体,用结构面所在的平面对其进行切割。然后,去除虚拟结构面,合并小的块体,形成复杂的块体。最后对这些复杂的块体进行稳定性分析。程序记录下计算过程中的相关数据,可以方便的进行查询显示。
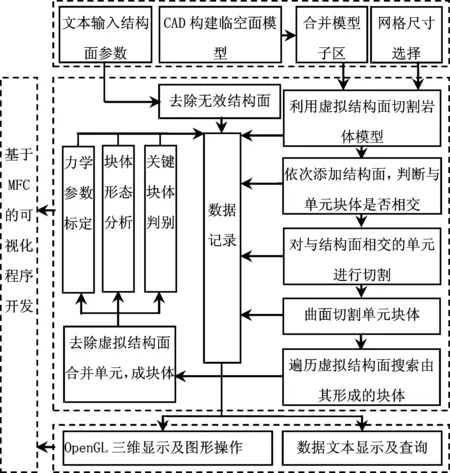
图1 块体系统构建流程图Fig.1 Flow chart of buiding block system
2 实现方法
2.1 块体数据结构
本次设计的块体识别算法要求块体之间、面之间保持数据的独立性,块体为多边形的集合,多边形为边的集合。采用图2所示的几何数据结构进行存储,利用C++中的CObArray类动态存储块体、面及边,块体类(CBlock)及面类(CPolygon)中封装表达自身属性的数据及针对这些数据进行操作的函数。这种数据结构完全忠实于工程实际,存储的数据数量不受限制,具有灵活易于操作,参数便于遗传等特点。

图2 块体数据结构Fig.2 Data structure of block
2.2 曲面对块体的切割
平面对多面体的切割算法目前已较为成熟,并有详细的实现过程(Yu et al.,2009;张敏思等,2016)。但岩体工程中的地下开挖面经常为曲面,在向岩体模型中添加开挖面时会面临曲面对单元块体的切割问题。
每个与其相交的块体都被分成两部分,切割方法如图3所示。块体的每个面内部,将所有棱线与曲面的交点组成一个线段。最后将每个面内得到的线段组成一个多边形,用这个多边形把块体分成两部分。但由于这个多边形是空间的,当其边数为3时,3条边一定在同一面内,当边数大于3时,多边形的边并不一定在同一面内,此时需要把这个空间多边形分成若干个平面多边形。当边数大于3时,任取此空间多边形的一条边,分别向与其相临的两边搜索,判断是否能在一个平面,若在同一平面则将其切开,形成一个新的面。在余下的边中继续使用此方法判断,直至剩下的线段数小于或者等于3。曲面对块体的切割是在岩体模型被划分网格后进行的,所有切割的对象都是小尺寸的单元块体,因此曲面实际上被转化为若干个小多边形的组合,图4展示了圆形开挖面对单元块体的切割。
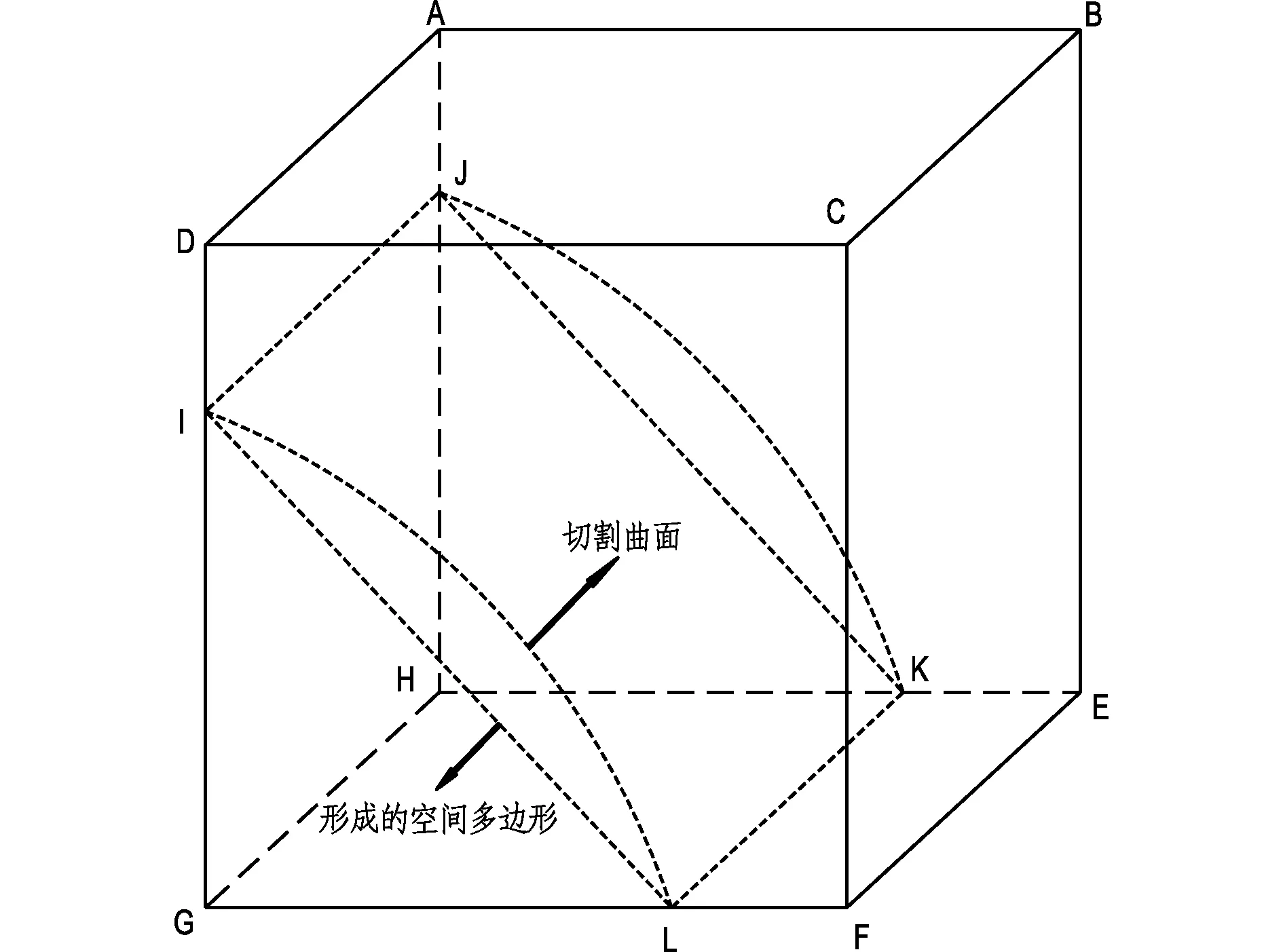
图3 曲面对单元块体切割示意图Fig.3 Cutting of element by curve suface
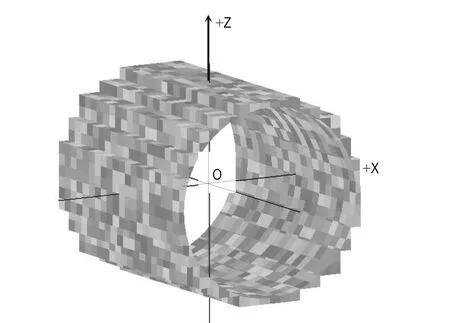
图4 圆形开挖面对围岩单元块体的切割Fig.4 Circle cut cell-block of surrounding rock
2.3 结构面与多边形的交线
图5为结构面与多边形交线的示意图,结构面与多边形的交线为BC和DE。令结构面与多边形所在平面分别为α,β,结构面圆心为O,半径为R。
(1)当时α∥β,结构面与多边形不相交。
(2)当圆心O到平面β的距离d≥R时,结构面与多边形不相交。
(3)当不满足(1)(2)时,求出平面α与β的交线l。
(4)求直线l在结构面内部的部分AF:把l转换到α面上的二维坐标系中,得出与结构面边界的交点A、F,再次转换到三维坐标系中。
(5)求直线在多边形内部的部分:把l转换到β面上的二维坐标系中,得出l在β面上方程为
(1)
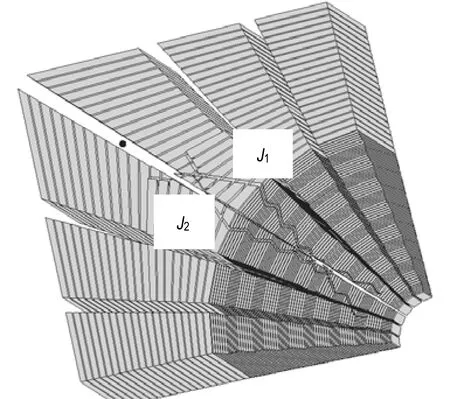
(6)求解L与多边形各边的交点参数并从小到大进行排序,t1 (7)求出(4)(6)中所得线段的交集,就是结构面与多边形的交线,若交集为空则不相交。直线l在结构面内的部分AF与l在多边形内的部分BC、DE相交于线段BC、DE,因此结构面与多边形的交线为BC和DE(图5)。 图5 结构面与多边形交线Fig.5 Intersecting line between structure plane and polygon 基于VC++提供的MFC进行可视化程序开发,调用OpenGL进行图形三维显示。嵌入比较流行的表格控件,实现结构面的输入及块体信息显示。采用两种方式建模,对于较为复杂的模型,读取dxf文件的面单元,转化为程序数据格式,构建岩体模型。对于简单的模型,可以采用对话框的方式进行快速建模。针对常见的实际工程,程序设计了边坡及隧道快速建模对话框。结构面参数可以从界面的表格中输入,也可以在txt中按照指定的顺序写好后导入,开发的程序具有良好的交互性。如图6所示,程序主要分为菜单区、图形显示区、图形操作区、数据输入及显示区。 图6 可视化程序界面Fig.6 Visual program interface 3.2.1 工程概况 图7为一露天矿多阶边坡,由两条结构面与边坡开挖面切割产生危岩体,存在较大安全隐患。经过实际勘测,J1产状为130°∠62°,粘聚力C1=0.15,内摩擦角φ1=29°;J2产状为310°∠68°,粘聚力C2=0.15,内摩擦角φ2=31°。由于开挖面不规则,且结构面未贯通,采用传统块体理论分析方法得到的危岩体体积不够精确,从而影响稳定系数的精度。 图7 多阶边坡Fig.7 Multi-step slope 3.2.2 块体系统构建 (1)构建临空面模型。选取危岩体临近区域(15 m×15 m×15 m)作为研究对象,在AutoCAD中采用647个四边形面单元构建临空面,同时初始化四边形方向,依照右手定则,以指向岩体内部的法向向量为正(图8)。 图8 构建临空面模型Fig.8 Modeling of rock slope (2)构建单元组成的岩体模型。采用投影法将临空面单元向OXY水平面上进行投影,得到由647个柱状单元体组成的岩体模型,柱状单元的侧面被设置为虚拟面,待切割结束后将其删除。投影所得柱状单元均为凸体,可采用虚拟结构面对其切割,完成进一步的划分网格。本工程仅存在两条大尺寸结构面,采用柱状离散单元足以满足精度要求。 (3)添加结构面切割单元。将两条结构面添加到所构建的岩体模型中,采用2.3所示方法,切割与其接触的单元块体,切割后单元块体数量变为792个。如图9所示,为了突出切割效果,采用炸裂方式显示模型的单元。 图9 结构面切割单元块体Fig.9 Discontinuity cut block (4)单元块体的合并及稳定性分析。切割完成后,删除柱状单元的侧面,导致块体间的合并,形成真实的块体,从而完成岩石块体系统的构建。图10为合并完成后的块体系统,产生的危岩体由45个单元聚合而成。采用极限平衡法对危岩体的稳定性进行计算,当块体沿双面i和j滑动时,稳定系数计算如下: 图10 块体单元合并Fig.10 Formation of block (2) 式中,Ni和Nj为作用在二滑动面上的法应力;Ci、φi和Cj、φj分别为滑动面i和j上的粘聚力及内摩擦角;Si和Sj分别为滑动面i和j的面积;Q为块体重量;α为滑动面i和j交线棱的倾角。得到危岩体体积为62.5 m3,稳定系数k=0.96。而采用传统方法只能将多阶边坡简化为单阶边坡,从而使构建的块体失真。图11所示为采用传统方法构建的块体模型,得到的危岩体体积为55 m3,稳定系数k=1.1。由此可见,计算结果的精准度取决于临空面模型的构建方法,比较结果显示本方法在此方面具有明显优势。 图11 传统方法计算结果Fig.11 Calculation result of traditional method (1)利用AutoCAD建立岩体临空面模型,可高效精准的描述复杂开挖面,从而使计算结果真实可靠。数据结构通用性强,可应用于其他通用软件。 (2)将有限结构面间对岩体的切割转化为对单元的切割,有效地避免了凹体的运算及处理,增强了程序的鲁棒性。 (3)采用MFC进行交互式开发,并调用OpenGL函数进行后处理,使得程序具有良好的操作性和可读性。
3 可视化程序开发及工程应用
3.1 可视化程序开发
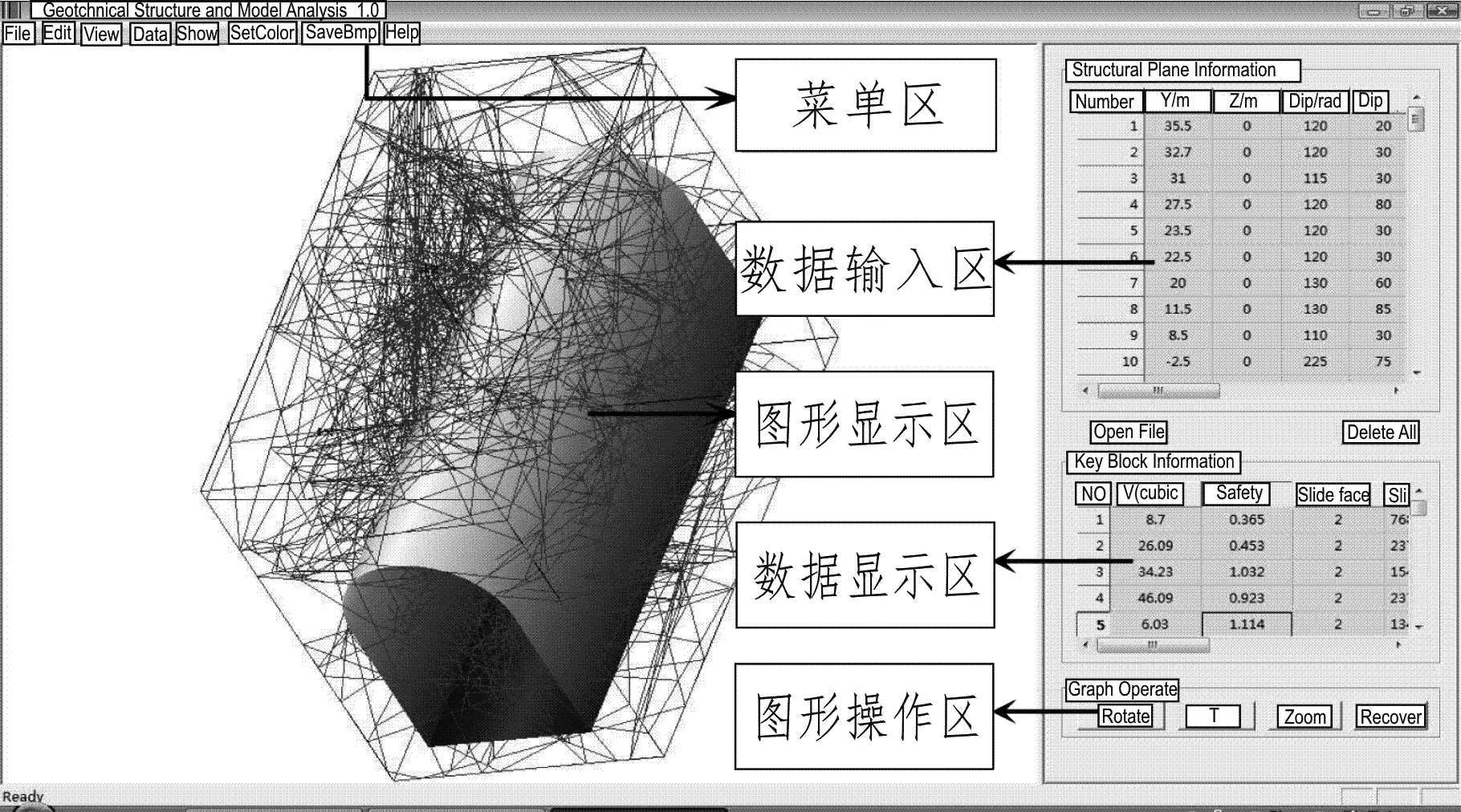
3.2 工程算例




4 结语
