基于安全经络图元诱因治疗的数学模型分析*
2020-09-12陈玉玲杨义先钮心忻
汤 卫, 陈玉玲, 杨义先, 钮心忻
1. 贵州大学 数学与统计学院, 贵阳550025
2. 公共大数据国家重点实验室(贵州大学), 贵阳550025
3. 贵州大学 计算机科学与技术学院, 贵阳550025
4. 北京邮电大学 网络空间安全学院, 北京100876
1 引言
近几年大数据行业呈现井喷式发展, 与之密切相关的系统和数据安全等成为社会广泛关注的焦点. 就网络系统的安全而言, 可以借助密码学中的公钥加密体制等进行保密运算, 以确保系统的运行能够符合现实需求. 这几年针对复杂网络系统的管理和控制问题, 杨义先等学者利用分解系统和检索定位的思想开展了相关的研究, 这成为密码学研究数据和系统安全的新思路[1–3], 是对密码学系统安全和数据保密理论的重要补充. 因此针对诱发系统不安全状态的诸多因素, 进行不安全事件的治理和控制是密码学研究的重要挑战[1,2].
系统的安全和发展是一个动态的过程, 核心目标是在安全的基础上实现高质量的发展, 一方面安全是发展的前提和必然要求, 另一方面发展为系统安全提供了更多的机会和保障. 在现实情境中, 分析复杂系统的安全性和控制策略是一个关键的问题, 尤其是如何对网络系统的不安全事件进行综合分析和治理是网络监管部门乃至全民的重要任务, 所以需要大力加强对系统安全的研究[1–6]; 在分析复杂系统的安全性时,若利用关联性原理将系统分解成若干个子系统, 那么系统的安全性就转化为各个子系统的安全性. 而子系统安全性的研究, 需要检索定位不安全系统内外两方面的诱因, 建立治疗机理并提出行之有效的策略来处理不安全问题. 对此过去密码学重点研究的是系统的加解密机制和访问控制策略, 对系统不安全事件的管理等没有进行深入分析, 随着《安全通论》和其他相关研究的深入[1–10], 利用不安全熵去定量分析系统安全已成为一种共识, 但是其分析方法大多限于思想和观念的分析, 并未展开详细的论述和研究[11–18], 因此尝试从系统诱因的视角利用状态转移过程中的不安全熵和效益变化来构建数学模型, 并分析系统安全控制问题.
自公钥密码理论问世以来, 网络安全模型的研究多是基于公钥加密和分级控制的理论和技术, 许多网络安全专家基于此对系统进行安全分析[4–10]. 为了改进密码学领域在分析网络系统基础研究方面的不足,许多专家都在致力于构建全面系统的网络安全基础理论并提出行之有效的创新性思想和方法.《安全通论》等[1–3]从宏观的视角出发利用安全与风险之间的对立统一关系, 基于信息熵的理论构建网络系统的不安全熵, 以动态发展的观点研究系统的不安全性问题, 并提出了系统安全经络图分解方法, 利用安全经络图的元诱因考察系统的安全性, 以此治疗系统元诱因和控制系统的安全态势, 虽然与网络安全有关的众多文献资料研究了如何利用现有技术确保系统的安全性, 但是在故障分析和策略选择等方面仍然还存在部分理论的不足[12–18]. 文献[1,2] 等在博弈论和系统论的基础上分析了黑客攻防模式和最佳攻击策略等, 但是在如何选择元诱因治疗的最佳策略和实践模式仍然没有做出详细的分析, 所以本文从基于元诱因的不安全事件分解的视角出发, 构建元诱因治疗的数学模型, 利用概率效益矩阵选择最佳元诱因治疗策略, 并依靠状态转移中的不安全熵等分析系统安全变化趋势, 期待为网络安全系统的管理和设计等提供参考和指导, 同时这也为研究系统安全的密码学理论提供了一种新的思路.
本文结构如下: 第2 节介绍安全经络图分解的相关知识和本文需要用到的一些相关概念; 第3 节给出基于元诱因治疗的数学模型和系统安全趋势的分析思路, 通过概率矩阵选择最佳的治疗策略组合, 并且用系统转移过程中的不安全熵和期望效益变化来刻画系统的安全趋势; 第4 节对分析系统不安全事件的治疗思路和方案, 并通过模拟仿真描绘系统状态变化趋势; 第5 节是对全文的一个总结.
2 基础知识
2.1 有限系统不安全事件的素分解

2.2 有限系统不安全事件A 的素诱因和元诱因分解
定义3[1]设X 是B 的一个真子集, 若P(B|X)>P(B), 则X 为B 的一个诱因.
定义4[1]设X 和Y 是B 的两个诱因, 同时满足X ∩Y =∅和B =X ∪Y, 则B 是可分解的, 并称X 和Y 是B 的两个素诱因; 如果B 的两个诱因X 和Y 不能继续分析, 那么称X 和Y 是B 的两个元诱因.
3 元诱因治疗的数学模型
3.1 系统安全经络图的绘制算法
有限系统的不安全事件A 按事件—素事件—素诱因—元诱因的四级分解体制进行分解, 并将分解的结果绘制成一棵倒生长的安全经络图(树), 具体步骤为:
(1) 将不安全事件A 分解事件为D1,D2,··· ,Dm, 其中Di∩Dj不一定是空集.
(2) 进一步对可再分解的事件Di分解为素事件B1,B2,··· ,Bs, 其中Bi∩Bj=∅.
(3) 对分解的素事件进行素诱因分解为R1,R2,··· ,Rt,Ri∩Rj=∅.
(4) 对非元诱因的素诱因进一步分解为元诱因c1,c2,··· ,cn.
在分解不安全事件时, 需要注意的是分解的前提是针对有限系统. 并且每一次分解都遵循定义1–4和定理1 和定理2 的分解原理, 在基于事件独立性和和事件概率的基础上进行分解.
在分解元诱因的过程中, 需要根据具体系统的结构特点进行事件和诱因划分, 每次分解的素事件和素诱因都可以继续在往下继续分解, 如此进行系统经络图绘制.
基于上述的分析, 有限系统不安全事件A 的安全经络图的算法如图1 所示, 同时给出基于算法的一个分解示意图.

算法1 有限系统不安全事件元诱因分解算法Input: Input system event A Output: output A = {c1,c2,··· ,cn}, graphA 1 A →{D1,D2,··· ,Dm}2 for i,j = 1 : N,and m ≤s ≤t ≤n ≤N,m,s,t,n ∈R do{D1,D2,··· ,Dm} = {B1,B2,··· ,Bs},s ≥m;5 end 6 if Bi = {R1,R2,··· ,Rj} then 3 if Di = {B1,B2,··· ,Bj}, then 4{B1,B2,··· ,Bs} = {R1,R2,··· ,Rt},t ≥s;8 end 9 if Ri = {y1,y2,··· ,yj} then 7 10 {R1,R2,··· ,Rt} = {c1,c2,··· ,cn}, n ≥t;11 end 12 graph A 13 end

图1 系统安全经络图绘制Figure 1 System safety meridian diagram drawing
3.2 元诱因治疗机理的函数构建和分析法
从图1 可知, 要治疗系统的元诱因可采取分而治之的策略, 按照至下而上依次治疗. 只要底层元诱因被治愈, 那么由该元诱因所决定的素诱因或者素事件就会被治愈, 即会引发不安全事件A 的自愈效应. 所以元诱因作为系统不安全的病因所在, 只要能够充分把握住元诱因的状态和发展趋势, 就能成功的把握系统的安全态势. 假设对于有限系统的不安全事件, 在没有受到刺激时, 元诱因由其内部属性及调节参数通过生成机制的作用形成, 即若系统的元诱因在受到刺激的作用时发生病变, 则构成诱因函数, 其中是刺激对作用后的病变元诱因.
假设对于有限系统的不安全事件A, 在没有受到刺激时, 元诱因yi由其内部属性q ={q1,q2,··· ,qn}及调节参数k = {k1,k2,··· ,kn} 通过生成机制κ 的作用形成, 即Y = κ{q,k}. 若不安全事件A 的元诱因yi在受到刺激ti的作用时发生病变, 则构成诱因函数ci=ϕ(yi,ti), 其中ci是刺激ti对yi作用后的病变元诱因.
在元诱因没有被激发的时候, 那么不需要对诱因进行治疗, 只需要严密观测每个元诱因的状态, 以及减少对元诱因可能产生作用的外部刺激. 此时的保护策略是制定一系列的安全预防机制, 并且针对每个元诱因设置不同的状态报警器, 按时汇总并分析元诱因的整体安全状态.
若元诱因在内部属性和刺激ti的综合作用下被激活并对系统产生了安全威胁, 为了保护系统的安全性, 则需对其诱因函数进行治疗. 治疗每个元诱因需对诱因函数进行反病因分析, 由于诱因函数ϕ 是由变量q,k,ti决定, 故一定存在相应的治疗原理f(q,k) 和f(ti), 综合诱因治疗原理构成治疗函数f(ci,ti). 治疗函数f 需要根据诱因函数ϕ 进行综合分析, 其目标是利用诱因函数使元诱因恢复到正常状态即yi=f(ci,ti). 由于导致不同元诱因病变的诱因函数不尽相同, 所以可以找到所有元诱因的诱因函数集合为ϕ={ϕ1,ϕ2,··· ,ϕm}, 因此同样也存在对应的治疗函数集合为f ={f1,f2,··· ,fm}, m ≥n.
在治疗元诱因时, 需要在治疗函数的基础上结合各种可用的现实资源或者治疗方法设计ci的治疗策略, 称为策略函数si= θ(fi,zi), 其中zi表示现实资源或条件. 在治疗元诱因时选用的不同策略形成的策略空间记为S ={s1,s2,··· ,sm)}={θ(f1,z1),θ(f2,z2),··· ,θ(fm,zm)}.
定理3 治疗函数f 是诱因函数ϕ 的逆向制约函数.
证明: 假设yi被激活为ci, 则可能是ci= ϕ(yi,ti) 中的q 或k 或ti发生了变化, 那么一定对应存在对应的属性、参数和刺激的治疗方法f(q,k) 和f(ti), 其中治疗方法是对ci的病因ϕ 进行逆向构建, 使ci=ϕ(yi,ti)回到安全状态,此时将治疗工具组合成治疗函数yi=f(ci,ti).从而可知f(ci,ti)是ϕ(yi,ti)的逆向制约函数.
注: 由于激活每个元诱因的诱因函数ϕi不尽相同, 所以针对元诱因yi的治疗函数fi就不会相同, 从而根据治疗函数fi设计的治疗策略si就不唯一. 即与每个元诱因对应的策略函数可以根据元诱因的具体情况进行调整和设计, 那么对于每个元诱因可能存在多个策略函数,

在检测硬件系统不安全事件A 的故障原因时, 需要按照不安全事件A 的现状, 并结合可能导致该现状的素事件和素诱因确定病因所在, 从而实现不安全事件A 的素诱因定位, 针对诱发该素诱因的元诱因进行仔细分析, 包括考察与元诱因有关的物理属性、结构属性和功能属性等, 若各属性正常, 则考察各个元诱因在受到黑客攻击ti的作用时如何引发不安全事件A, 从而寻找到导致系统故障的诱因函数, 进而再建立对应的治疗函数. 根据对计算机网络系统中多数的系统底层元诱因的分析, 可以把黑客攻击不安全事件A的主要属性和诱因函数分析如下.

编号 属性名称 属性描述 元诱因构成方式 元诱因受损模式q1 物质属性 构成元诱因的基本物理元件 以物理性和物质状态的基本原理体现 相关物质被损坏等q2 结构属性 体现元诱因的组成机制和模式 元诱因的基本组成原理和构造方式 元件结构受损或紊乱等q3 功能属性 表示元诱因基本功能属性状态 以实现的功能需求为主导, 形成功能的关联 功能元件丢失或失调等q4 数值属性 元诱因的逻辑参数和相关数值 元诱因的基本参数集合和形成的特征数据 数值缺失和参数错误等
表1 中, 将不安全事件A 的元诱因属性分为上述四个方面, 并且当黑客选择攻击系统时, 总可以选择对元诱因的物理元件或功能结构等进行攻击. 黑客等在攻击系统时需要对这些属性进行分析和处理, 每个属性对应着不同的属性值, 重点是弄明白每个属性的作用和属性之间的相互影响. 下面我们把导致不安全事件A 可能遭受的主要刺激(攻击方式) 归纳如下.

编号 名称 诱因函数 诱因函数描述 治疗函数 治疗函数描述t1 物理攻击 ci = w1(yi,t1) 对相关元诱因的属性状态施加物理攻击或其他黑客攻击, 使得元诱因物理受损yi = f1(ci,t1) 修复更换受损元件, 入侵检测和设置防火墙, 多层物理隔离等方法t2 共谋攻击 ci = w2(yi,t2) 某管理员私下泄露系统密码文件 yi = f1(ci,t2) 加强管理, 数据加密备份,更新密码方案和协议t3 木马病毒 ci = w3(yi,t3) 通过电子邮件或系统漏洞将病毒程序代码安装到目标用户, 并使之运行yi = f1(ci,t3) 查杀病毒, 安装补丁, 安装防火墙, 修补系统程序漏洞t4 拒绝服务 ci = w4(yi,t4) 通过占用系统服务器或者CPU的运行内存等让系统陷入瘫痪,终止网络服务等yi = f1(ci,t4) 进行系统加固或重载服务器等措施
表2 通过分析黑客攻击系统的部分途径和方法研究元诱因的病变函数和治疗函数, 从而对系统不安全事件采取不同的治疗策略进行处理. 对于实例中的诱因函数集ϕ = {ϕ1,ϕ2,ϕ3,ϕ4} 和治疗函数集f ={f1,f2,f3,f4}, 通过结合现实资源和方法形成相应的治疗策略S ={s1,s2,s3,s4}.
3.3 基于概率矩阵和期望效益的元诱因治疗分析
在研究不安全事件的治疗方案时需要考察各个病变元诱因的治疗策略, 即在治疗过程中, 如何选择出最佳的治疗策略组合{s1,s2,s3,s4} 去治疗病变元诱因{c1,c2,c3,c4}
对病变元诱因的治疗需要考察每个治疗策略对不同元诱因治愈的概率大小, 同时还要考察不同治疗策略治疗元诱因的期望收益. 在选择最佳治疗策略组合时, 可按照不同策略治愈元诱因的概率结合治疗成本及期望效益等共同决定, 使得治疗策略组合能够获得治疗总收益最大化.
假设si治愈ci的概率记为p(ci|si), 那么不同治疗策略治愈不同元诱因的概率矩阵如下

此时若仅考虑从每个策略治愈的概率大小进行策略选择, 那么按照治愈概率大小剔除劣势概率策略就可以找到最佳的治疗策略组合. 但是由于不同策略治愈元诱因成本不一样, 产生的收益也会有差异, 若在治疗系统前, 计算出治疗元诱因的系统期望收益和总收益, 则按照期望收益和总收益的情况进行策略选择比按照概率进行选择更具合理性.
对于系统不安全事件而言, 正如不同构成要件对系统整体产生的影响值不同一样, 所以每个元诱因对不安全事件乃至整个系统产生的影响不同. 假设元诱因ci对系统产生的期望效益影响值为mi时, 那么治愈单个元诱因的期望效益值可记为Ei= p{ci|si}mi. 如果治疗元诱因花去成本为αi, 那么此时治愈单个元诱因的收益为Ri=Ei−αi.
因此, 若各个元诱因对A 的期望效益影响值分别为{m1,m2,··· ,mn}, 治愈不同元诱因的成本为{α1,α2,··· ,αn}, 则根据不同治疗策略的概率矩阵可计算出治疗系统的所有元诱因所获得总收益为
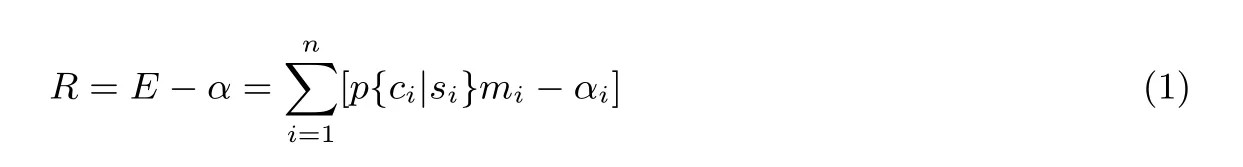
其中si(i = 1,2,··· ,n) 是病变元诱因ci的治疗策略之一, E 和α 分别表示治疗元诱因所获得的总期望效益和花去的总成本, 包括经济成本和时间成本.
那么根据公式(1), 从矩阵P 中选出每个病变元诱因的治疗策略si, 则根据元诱因成本α, 期望效益影响值m 去计算治疗元诱因的期望效益和总收益如表3 所示.

C →Y C →y1 C →y2 ··· C →yi ··· C →yn s1 s2 ··· si ··· sn m m1 m2 ··· mi ··· mn α α1 α2 ··· αi ··· αn s E E1 E2 ··· Ei ··· En R r1 = E1 −α1 r2 = E2 −α2 ··· ri = Ei −αi ··· rn = En −αn
对不安全事件的治疗成本和效益影响值需要根据具体的系统环境和现实情况进行计量, 一般数据来自于对大量数据的统计分析整理获得. 在元诱因的治疗过程中, 由于一个元诱因可能存在多个可供使用的策略, 且不同策略对不同元诱因产生的利润不同, 则根据概率矩阵和成本损耗等算出治疗的期望效益和总收益, 对治疗收益值的大小顺序进行递减排序, 利用剔除劣势策略的方式找到最优策略来迅速找到最佳的元诱因治疗策略, 即最优策略组合为

3.4 状态转移中的安全趋势和收益变化分析
3.4.1 系统状态转移与安全趋势分析
若不安全事件A 的元诱因经过一轮治疗后由初始状态Z0转变为状态Z1, 并从状态Zi转变到状态Zi+1. 假设存在状态转移函数为中T : Zi×S →Zi+1, 其中T(Zi,s,Zi+1),i = 0,1,··· ,n 表示对Zi状态的元诱因执行策略组合S 后转为状态Zi+1. 在状态转移过程中, 因为经过治疗之后的元诱因可能被治愈, 也可能没有被治愈, 同时可能还有新的元诱因被激活, 所以系统的安全性就会随着元诱因治疗的过程不断地发生安全趋势变化, 而所采用的基本策略空间S 前后保持不变, 所以对系统的安全性我们进行深入的分析.
定义5[1]在一个有限系统的不安全事件A 中, 若元诱因造成系统的不安全性用自安全量I(ci) =−log p(ci) 表示, 则不安全事件A 的安全性大小可以用自安全量的概率加权的平均值来度量, 即自安全量的数学期望不安全熵来刻画如下

其中p(ci) 表示元诱因yi病变ci为的概率.
对系统的整体安全性, 可以考察系统在治疗过程中的前后状态的不安全熵的变化趋势, 利用不安全熵的增量变化趋势指导元诱因的治疗. 假设记系统的不安全熵增量为
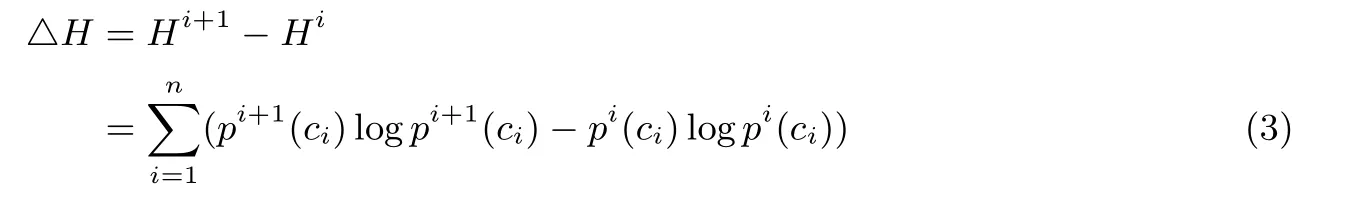
从上式可以计算出不安全熵随着状态转移的变化情况, 根据系统前后状态的熵增量可定量研究系统的安全状态. 即系统不安全熵增量变化状况可分为以下几类情况进行分析.
(1) 若△H = 0, 表示系统不安全事件A 的前后两个状态没有发生不安全熵的变化, 但是从时间的角度来说, 系统的安全性保持稳定. 此时系统由上一个状态到达当前状态, 可能是由于被激活的元诱因未被成功治愈, 或者是系统没有发生新的元诱因被激活, 或者是激活的元诱因和被治愈的元诱因对系统不安全熵的影响等价抵消.
(2) 若△H > 0, 系统不安全事件件A 的不安全熵减少, 此时系统变得比以前更加安全了. 发生这种情况主要是由于系统的元诱因被成功治愈或者是系统采取加固措施对元诱因进行加固, 此时前一状态的不安全熵高于当前状态的不安全熵.
(3) 若△H <0, 系统不安全事件件A 的不安全熵发生增加. 此时可能是元诱因被外部刺激成功激活,或者是新激活的元诱因对系统产生的影响大过被治愈的元诱因导致的影响.
在研究系统的不安全性方面, 采取措施对系统元诱因进行治疗, 为的就是将系统的不安全因素清除或者加固系统元诱因, 减少系统的不安全熵. 那么在多轮的系统元诱因治疗过程中, 系统应该尽量保证自身的不安全熵能够逐渐减少或者保持平稳以使得系统不发生安全事故, 从而促进系统整体状态变好.
3.4.2 状态转移中的期望收益和安全性分析


按照3.4.1 对不安全熵的定量研究方法, 可以分为以下几类情况对期望收益进行分析.
(1) 若△R = 0, 表示系统不安全事件A 的前后两个状态没有发生收益的变化, 这说明对系统没有产生新的收益.
(2) 若△R < 0, 系统不安全事件的收益减少, 此时系统变得总价值减少. 这时需要加强对系统的管理和投入.
(3) 若△R>0, 系统不安全事件的收益发生增加, 符合对系统的价值的追求.
在研究系统的收益方面, 采取措施对系统元诱因进行治疗, 是为将系统的不安全因素清除和加固元诱因, 增加系统的收益.
在实例中, 假设系统不安全事件A 的不安全熵和期望收益随着病变元诱因被治愈的状态变化而变化,其中对其不安全熵的三种可能情况记为{△H >0,△H =0,△H <0}={1,0,−1}, 期望收益的三种情况也可以记为{△R > 0,△R = 0,△R < 0} = {1,0,−1}. 在分析系统的不安全状态和收益变化两方面的因素时, 需要根据两者的边缘趋势变化来分析系统的联合变化趋势, 从而决定如何有针对性的选择治疗策略.
对于系统的发展和安全趋势来说, 最佳的状态是不安全熵减少, 收益值增加, 即{△H > 0,△R >0} = {1,1}. 在进行系统管理的过程中, 经常不能实现两者的共赢, 那么在管理者的利益需求和安全需求的双向要求下如何进行协调成为重要的问题. 根据发展和安全的辩证关系, 系统应该追求在相对安全下的最佳利益, 所以我们首先关注系统不安全熵的变化趋势问题, 只有系统在越来越安全的情况才能实现有价值的发展需求. 所以最佳的状态为{△H > 0,△R > 0} = {1,1}, 如果在无法两者兼顾的情况下以不安全熵为先, 然后追求利益最大化.
表4 是对不安全熵和收益的边缘变化趋势和联合变化趋势的分析. 当△R > 0 和△H > 0 时记策略值为1, 当△R=0 和△H =0 时记策略值为0, 当△R<0 和△H <0 时记策略值为−1. 在熵策略和效益策略两个维度的策略选择上, 根据博弈论的基本原理可知, 最佳的均衡点是{1,1}.
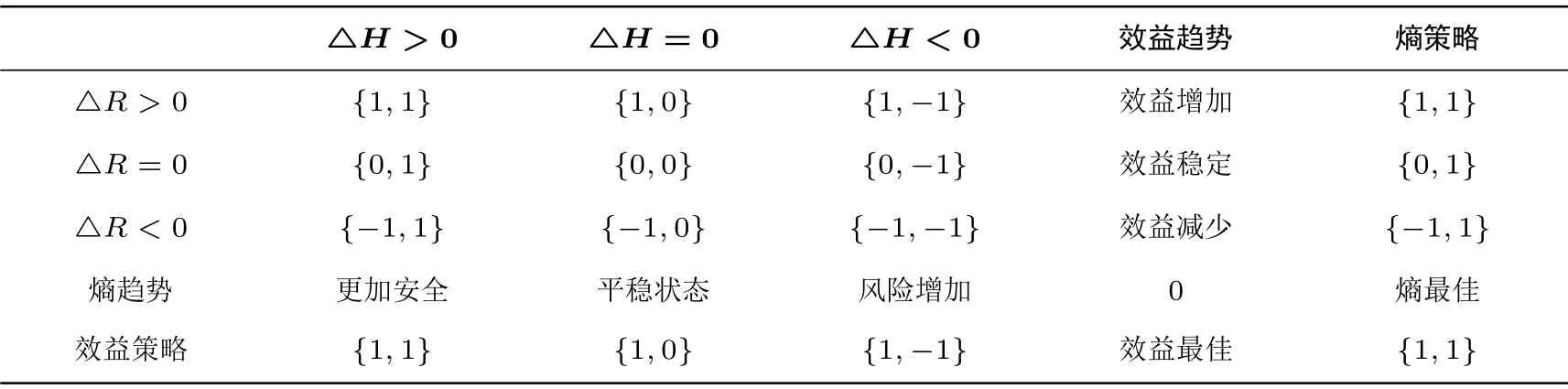
△H > 0 △H = 0 △H < 0 效益趋势 熵策略△R > 0 {1,1} {1,0} {1,−1} 效益增加 {1,1}△R = 0 {0,1} {0,0} {0,−1} 效益稳定 {0,1}△R < 0 {−1,1} {−1,0} {−1,−1} 效益减少 {−1,1}熵趋势 更加安全 平稳状态 风险增加 0 熵最佳效益策略 {1,1} {1,0} {1,−1} 效益最佳 {1,1}
经过一轮治疗后, 因为部分被激发的元诱因被治愈, 所以系统的不安全熵减少, 系统趋向于更安全的状态, 同时这样状态也会为系统带来经济收益, 如果经济收益也同时增加说明这样的治疗策略是所有策略中的双赢策略. 前面对治疗策略的选择是根据被激活元诱因被治愈的可能性大小进行劣势策略剔除留下的优胜策略, 但是没有对策略引起的安全趋势和效益做深层次分析, 此处相当于是对策略选择的一个重新证明和反向印证, 这对改进策略选择有着很好的帮助. 一般来说对元诱因越有效的策略也会带来更多的收益.
对系统不安全事件实施多次治疗, 需要根据每个系统安全变化趋势展开系统论证和分析. 随着被激活元诱因不断被治愈, 新的元诱因也会因为各种外界原因重新被激活, 正如黑客生存规律符合系统自我平衡的生物学定律一般, 系统的安全趋势最终会趋向于一个动态的稳定值, 元诱因的生存状态是此起彼伏的.
4 元诱因治疗实践分析与模拟仿真
通过第3 节对元诱因治疗数学模型的分析, 可将基于安全经络图的元诱因治疗过程分为四个阶段.
(1) 综合分析阶段. 本阶段的主要任务包括对有限系统A 的安全经络图分解和绘制, 通过寻找元诱因的内外属性和形成机理去构建诱因函数和与之相对应的治疗策略, 对已激活的元诱因进行综合分析.
(2) 策略决策阶段, 本阶段的主要任务是利用阶段(1) 形成的数据信息去计算元诱因治疗的概率效益矩阵, 为有限系统A 的所有元诱因选取到最佳治的疗策略组合, 并在此基础上展开元诱因的治疗. 治疗时尤其关注内外环境的变化和可供利用的资源, 要充分使用各项有效资源进行治疗.
(3) 效果反馈阶段. 通过对元诱因的治疗之后考察治疗的元诱因状态和效益转移情况, 并根据治疗前后状态的不安全熵和效益状态的变化趋势分析治疗的效果如何. 在治疗中通过分析状态的转移及时发现问题所在, 利用反馈的治疗效果更好地进行管理和决策服务.
(4) 迭代调整阶段. 经过效果反馈和诱因进一步寻找以及对治疗策略和相关状态的深入分析, 充分考虑从一轮治疗到多轮治疗的过程中怎么进行治疗策略迭代调整, 对每一轮的治疗都要做到及时有效最优的目标, 示意图如图2.
上述四个阶段是按照分析反馈迭代调整的治疗思路对元诱因进行治疗, 在治疗过程中的创新变化和策略组合调整等需要根据具体情况具体分析.
对于计算机网络遭受黑客攻击的不安全事件而言, 主要的元诱因事件有病毒攻击、系统漏洞攻击、欺诈类攻击和木马攻击四个, 同时针对这四个攻击的治疗策略主要包括访问控制策略、网络信息加密策略、入侵检测策略、防火墙策略、秘钥管理策略和漏洞补丁策略等.
在进行计算机不安全事件元诱因治疗时, 首先对于上述黑客攻击事件, 按照3.3 和3.4 中对实验数据的要求搭建实验环境, 并在多次模拟攻防实验中, 针对系统的不安全事件采集相关的数据, 然后利用采集的数据统计分析出不安全事件的4 个元诱因的基本信息和相关治疗策略, 最后按照不同策略治愈元诱因的概率P、治疗成本α 等计算效益.
基于采集的数据在总结经验并计算出实验参数的基础上, 然后利用模拟实验数据画出在不同治疗策略下计算机网络系统遭受黑客攻击时的元诱因治愈概率对比图3.
从图3 可知, 针对不同的黑客攻击方式可以采取不同的治疗策略来治疗系统元诱因. 由于每个治疗策略的治疗效果各不相同, 所以应充分考虑从治疗策略的实用性和治愈概率大小等角度选定治疗策略.
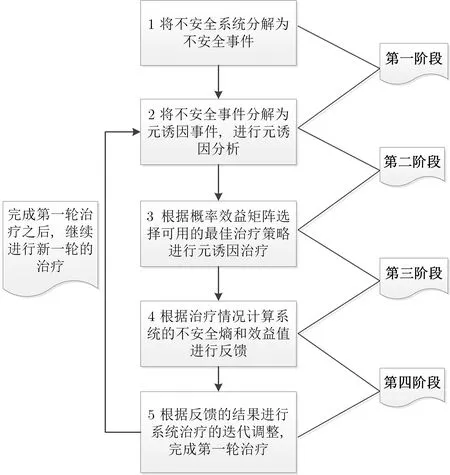
图2 元诱因治疗的执行思路和策略路径图Figure 2 Map of implementation thoughts and strategies of meta-inducement therapy

图3 不同策略下病变元诱因被治愈的概率对比图Figure 3 Comparison diagram of the probability of cure of pathologic factors under different strategies
同时还可以利用模拟的数据按照公式(3)和(4)计算出系统在黑客攻击状态下的不安全熵和期望效益,从而可以画出这两者随着系统不安全概率变化的趋势图. 在模拟的元诱因治疗数据中, 我们针对每个治疗策略对系统产生的期望效益影响值进行合理化设计, 并且根据治疗策略对系统不安全熵和产生效益变化趋势的情况进行模拟数值分析, 并给出趋势图如图4.
从图4 可知, 系统不安全事件被治愈的概率越高, 那么系统的不安全熵就越低. 即系统越安全的时候系统的不安全熵就会越低, 符合治疗的目标.
图5 显示出系统的期望收益因治愈系统元诱因的概率变化而变化, 即系统的期望收益随着系统元诱因被治愈概率越高则期望收益越大. 一般情况下两者是正比关系, 但是期望收益与治疗成本和治愈概率等因素有关, 所以在进行策略计算时需要综合考察成本、影响值和治愈概率等因素. 由此看来, 系统的不安全熵和期望收益是开展元诱因治疗的两个重要目标, 所以掌握两者的变化趋势是十分重要的.
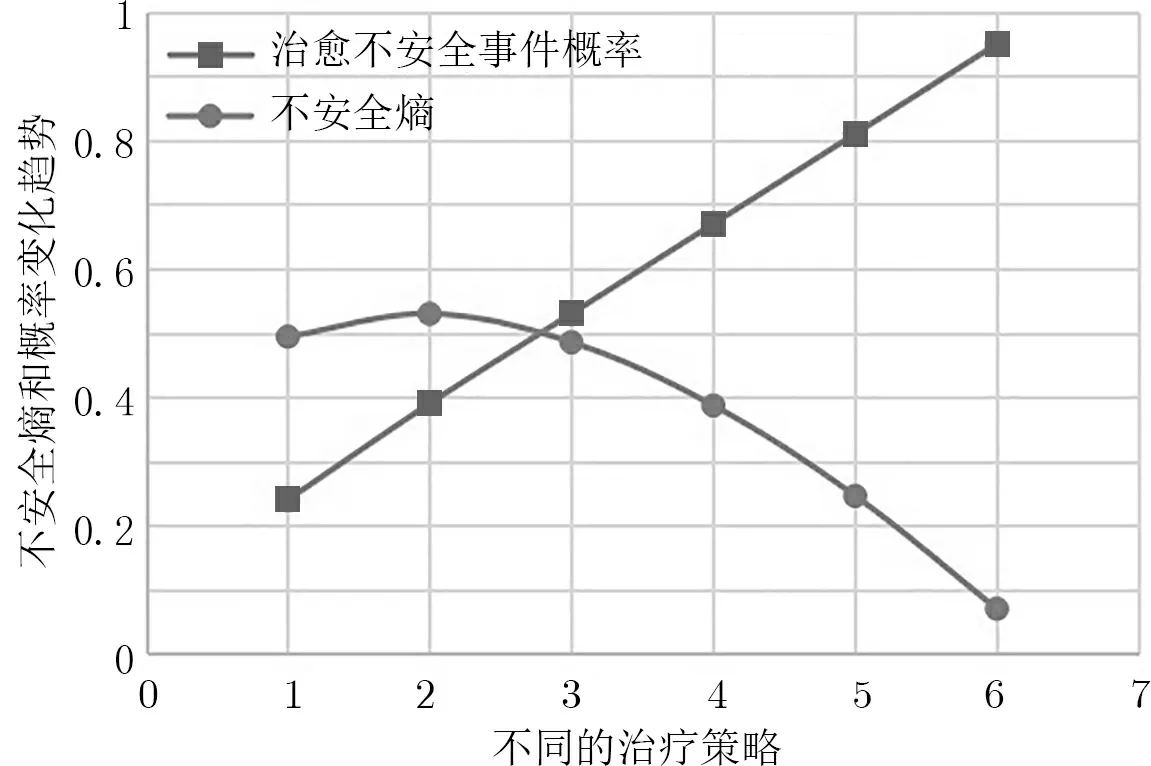
图4 不同治疗策略下系统不安全熵和概率变化图Figure 4 Changes of system unsafe entropy and probability under different treatment strategies
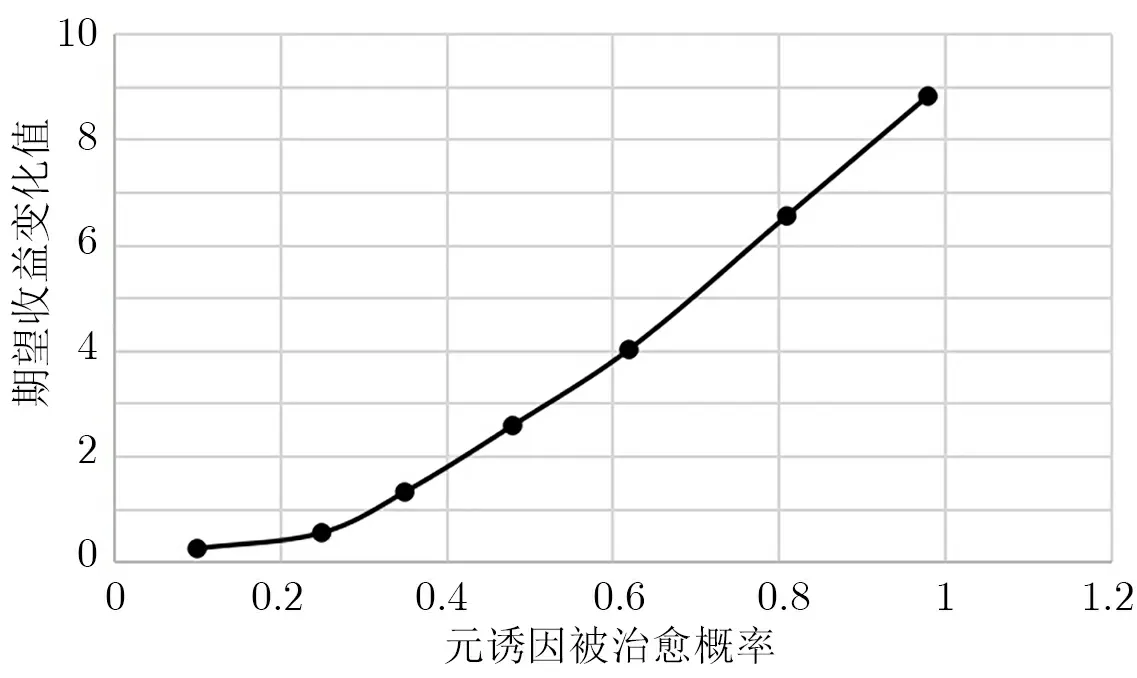
图5 系统期望收益随着治愈概率变化的趋势图Figure 5 Trend chart of system expected revenue changing with treatment probability
5 结论
本文通过对有限系统不安全事件元诱因治疗模型的分析得出以下几点结论: 首先, 任何有限系统的不安全事件都可以通过系统安全经络图进行诱因检索和分析, 利用系统的元诱因结构设计系统的管理和整治方案, 对加强系统的安全控制等有着非常重要的作用; 其次, 借助对系统状态转移过程中元诱因不安全熵和效益随状态转移的分析, 帮助系统管理员通过调整状态转移过程的参数来促进系统状态朝向预定目标转变; 再次, 本文结合信息论和密码学的研究成果进行模型构建, 利用系统不安全熵增量和效益变化情况来分析系统的整体安全性, 这方便于在进行系统安全控制和管理时依照相关原理设计相应的安全状态警报器, 以不安全熵作为参考依据进行严密观测和处理; 最后, 我们给出一个行之有效的元诱因治疗思路, 有助于实现网络系统不安全事件的全面控制和精准治理, 同时也可以促进密码学对系统安全控制等的研究, 对增强整个网络系统的安全和进行数据保密分析等方面也有着重要的意义.
本文是基于在密码学网络安全研究的大框架下对系统的不安全事件进行研究, 属于密码学研究的一个新视角. 虽然模型已对元诱因治疗策略等进行了分析, 但是对攻防体系中的元诱因相互关联性等问题还没有进行论述, 这是未来需要重点考虑的重点工作之一, 在此基础上我们可以继续分析在攻防体系中的元诱因治疗方案.
