误差异分布概率预报模型在运河站洪水预报中的应用研究

董家根， 胡义明， 罗俐雅*， 梁忠民

(1.江苏省水文水资源勘测局， 江苏 南京 210029； 2.河海大学水文水资源学院， 江苏 南京 210098)

1 概 述

洪水预报是流域防洪减灾工作中重要的非工程措施。由于自然水文过程的复杂性和人类认识水平的局限性，洪水预报不可避免地存在诸多不确定性，从而导致洪水预报结果的不确定性。为了定量描述洪水预报的不确定性，洪水概率预报理念逐渐获得重视，成为水文预报领域的重要研究热点之一。

纵观国内外诸多洪水概率预报方法，大体可分为全要素耦合和总误差分析两大类途径[1]。全要素耦合类方法是在识别和量化降雨—径流过程各环节不确定性要素基础上，通过耦合各要素的不确定性，最终实现概率预报，如贝叶斯总误差分析方法[2]、贝叶斯综合不确定性估计方法[3]等。总误差分析类方法是直接对预报结果的不确定性进行量化，而不处理预报各环节的不确定性，最终以预报量后验分布的形式实现概率预报，如贝叶斯概率预报系统[4-5]、模型条件处理器法[6]等。考虑到不同流量量级下洪水预报误差不同，在误差总分析框架下发展了若干典型的考虑预报误差异分布的概率预报方法，如Steenbergen等[7]构建了三维误差矩阵以反应不同洪水量级预报误差分布规律的不同；梁忠民等[1]通过构建预报误差的均值与流量的定量关系，进而提出了误差异分布概率预报模型，实现了洪水概率预报。

本文在分析运河站的洪水预报误差统计规律基础上，采用误差异分布概率预报模型开展洪水概率预报研究，提供洪水预报倾向值和预报区间成果，丰富了运河站的洪水预报信息。

2 方法原理

2.1 误差异分布概率预报模型

误差异分布概率预报模型考虑了不同洪水量级下洪水预报误差的非平稳性特征[1]。若将Y和M分别记作预报量的真实值及确定性预报值，(Y，M)代表了至预报时刻所能获取的所有历史信息，则未来t时刻预报量yt的预测不确定性可以记作f(yt|mt，Y，M)，其中，mt为t时刻的确定性预报值。预报误差为

(1)

由于模型预报值在预报时刻是已知量，则t时刻预报量yt可以视作预报误差的函数，即，

yt|mt=B(ε)

(2)

式中，B(ε)为预报误差的函数。

则预测不确定性可以写作：

f(yt|mt，Y，M)=f(B(ε)|Y，M)

(3)

即f(yt|mt，Y，M)的推求可以转化为误差条件概率g(ε|Y，M)函数的概率分布推求问题。假定预报误差的先验分布为正态分布，即，

ε～N(μ,σ2)

(4)

式中，μ为误差先验分布均值，σ为误差先验分布标准差。

大量研究发现，预报误差的分布函数与流量级别密切相关，因此假定误差的均值与标准差和流量具有函数关系：

E(ε|Y，M)=H(Mt)

(5)

Std(ε|Y，M)=L(Mt)

(6)

式中，E为均值函数，Std为标准差函数，H和L为函数关系，其具体形式不定。由此可以推得预报误差的后验分布：

(7)

因此，结合式(3)可以推得预报量的条件概率分布为

(8)

2.2 预报评价指标

概率预报模型在提供定值预报(如中位数预报Q50)的同时，还可以提供某一置信度下的洪水预报区间(如90%预报区间)，为此，概率预报成果的评价可以分为定值预报成果评价和预报区间成果评价。具体而言，针对定值预报结果(Q50)，采用如下3项指标进行预报精度评价。

(1)次洪径流深相对误差

ΔR=[(Robs-Rc)/Robs]×100%

(9)

(2)洪峰相对误差

ΔQm=[(Qm,obs-Qm,c)/Qm,obs]×100%

(10)

(3)确定性系数

(11)

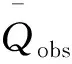
针对预报区间成果，采用如下2项指标进行评价：

(1)覆盖率

(12)

(2)离散度

DI=(qui-qdi)/Qi,obs

(13)

式中，qui、qdi分别为第i时刻概率预报区间(具有某一置信度，如90%)的上、下限；Qi,obs为第i时刻实测流量；N为预报总时段数。

3 应用研究

3.1 确定性预报

本次选取运河站以上流域2003—2010年间10场洪水进行新安江模型的率定与验证，其中，2003—2008年间的8场洪水用于模型率定，2009—2010年间的2场洪水用于模型验证，计算步长Δt=2 h。表1给出了新安江模型参数的率定结果，表2给出了洪水预报精度的统计结果。

表1 新安江模型参数率定结果

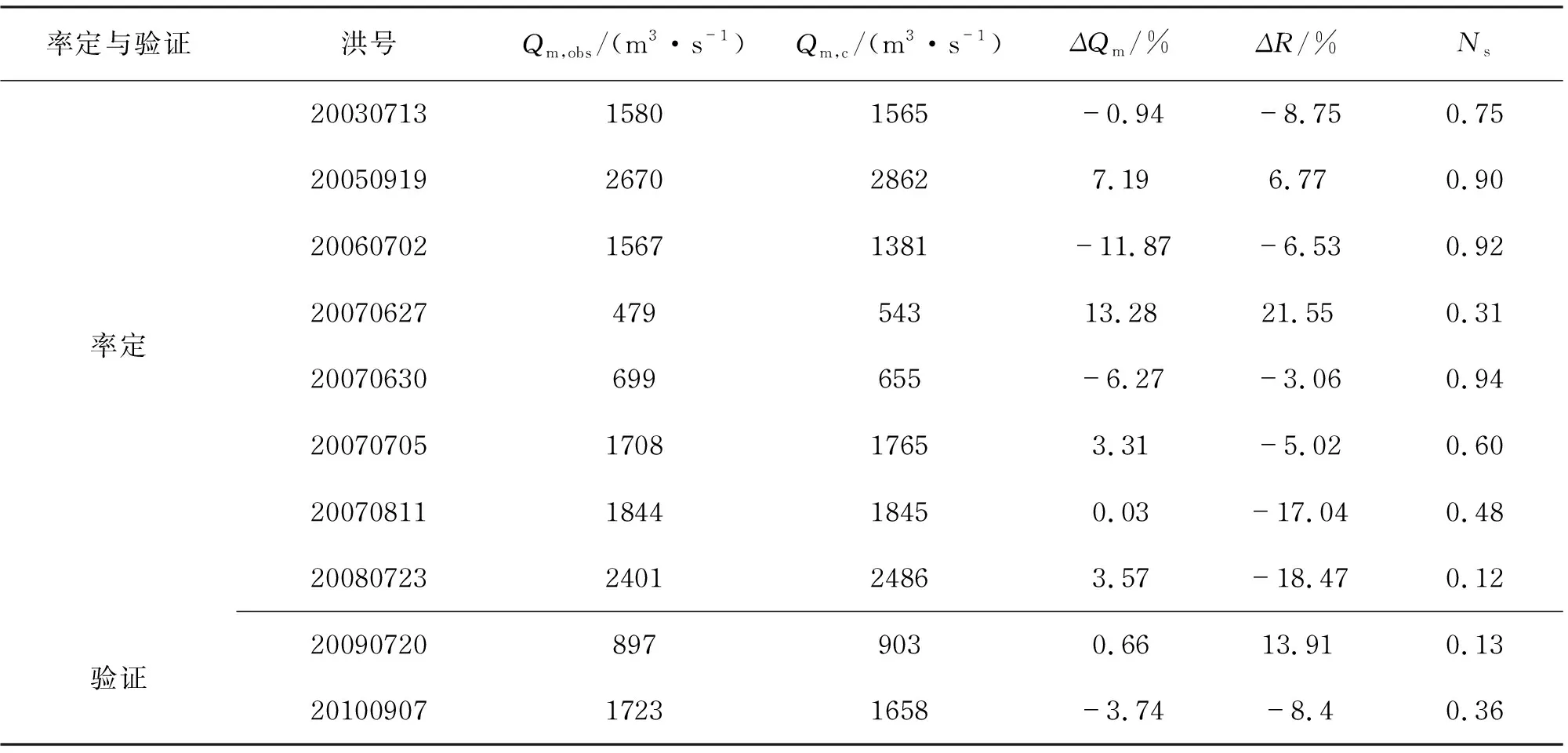
表2 率定期和验证期洪水模拟效果分析成果

由表2可以看出，场次洪水洪峰相对误差均在15%以内，除20070627场次外，其余场次洪量相对误差均在20%以内，平均确定性系数为0.55。

3.2 预报误差分析结果

基于新安江模型的模拟预报结果，分析了上述10场洪水预报相对误差与新安江模型预报流量值的关系，如图1所示。

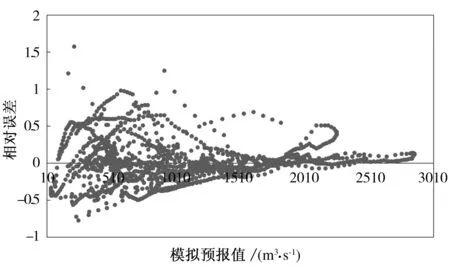
图1 预报相对误差与新安江模型流量预报值关系

由图1可知，高、低流量预报值呈现出不同的相对误差特征规律，高流量预报值的相对误差变幅较小，而低流量预报值的相对误差变幅较大。为进一步分析预报相对误差的统计规律，根据预报量的大小对预报量进行分组，求得不同组别预报相对误差的均值与标准差，进而绘制误差均值与误差标准差变化趋势，如图2所示。

图2 相对误差均值和标准差与确定性预报值关系

由图2可知，相对误差均值、标准差随模型预报值呈线性变化：模型预报值在0～504 m3/s时，相对误差均值随预报值呈递增趋势；预报值在504～943 m3/s时，相对误差均值呈递减趋势；预报值在943 m3/s以上时，相对误差均值再次呈递增趋势。模型预报值在0～1 090 m3/s时，相对误差标准差虽波动较大，但总体呈递减趋势；预报值在1 090～1 290 m3/s时，相对误差标准差也呈递减趋势，但递减趋势变大；预报值在1 290 m3/s以上时，相对误差标准差仍呈递减趋势，但递减趋势变缓。

由于相对误差均值、标准差与预报值呈现分段线性关系，为此，采用分段线性方程进行拟合，拟合效果如图3所示。

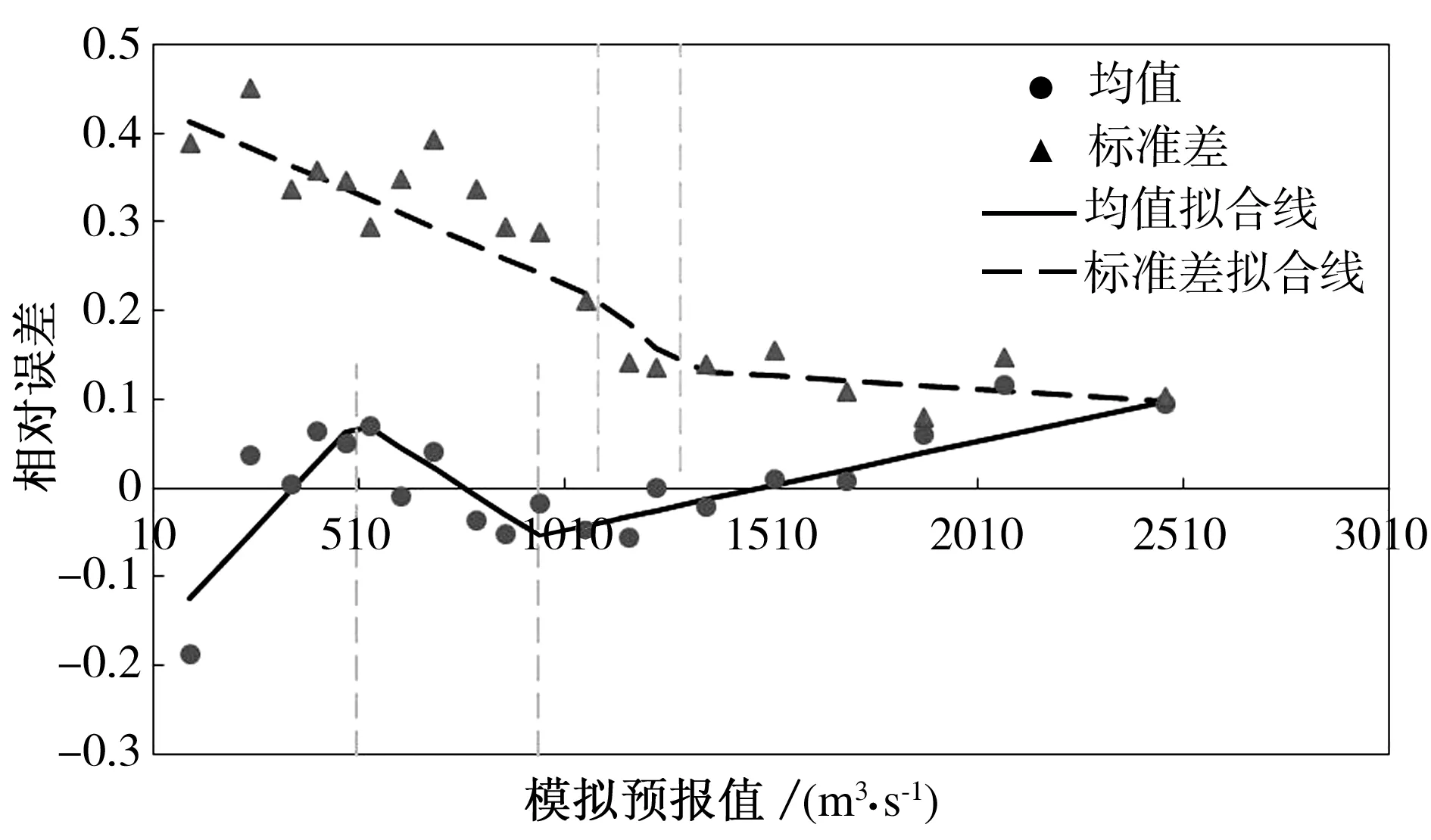
图3 相对误差均值、标准差与预报流量拟合

3.3 概率预报结果

根据预报流量的概率密度函数，计算中位数预报结果(Q50)和90%置信水平对应的预报区间。采用次洪径流深相对误差、洪峰相对误差及确定性系数评估中位数预报结果的精度，采用覆盖率和离散度指标评估预报区间成果的可靠性。评价结果见表3。

由表3可以看出，就概率预报模型提供的中位数(Q50)定值预报结果而言，10场洪水的次洪径流深相对误差、洪峰相对误差均在20%以内；10场洪水的次洪径流深相对误差绝对值的平均值为9.6%，洪峰相对误差绝对值的平均值为5.3%，确定性系数平均值为0.69；就概率预报模型提供的90%置信区间而言，10场洪水的平均覆盖率达93.4%，平均离散度为1.2，表明90%预报区间能覆盖绝大多数的实测数据。

表4给出了概率预报模型提供的中位数(Q50)定值预报结果与新安江模型原始预报结果的精度对比分析结果。由表4中可知，概率预报模型提供的Q50定值预报结果要优于新安江模型原始预报结果的精度，经概率预报模型处理后，10场洪水的平均确定性系数由0.55提高到0.69，确定性系数大于0.5的洪水场次数由5场提高到8场；10场洪水的次洪径流深相对误差绝对值的平均值由11.0%减小到9.6%；洪峰相对误差绝对值的平均值由5.1%到5.3%，无明显差异。

为了更为直观地显示概率预报模型的预报效果，图4提供了20050919场洪水的新安江模型预报结果、概率预报模型的中位数Q50预报结果、90%置信度下的预报区间结果以及实测流量过程对比图。从图4可知，概率预报模型提供的Q50定值预报与实测流量过程更为吻合，且90%预报区间可以覆盖绝大多数的实测流量。

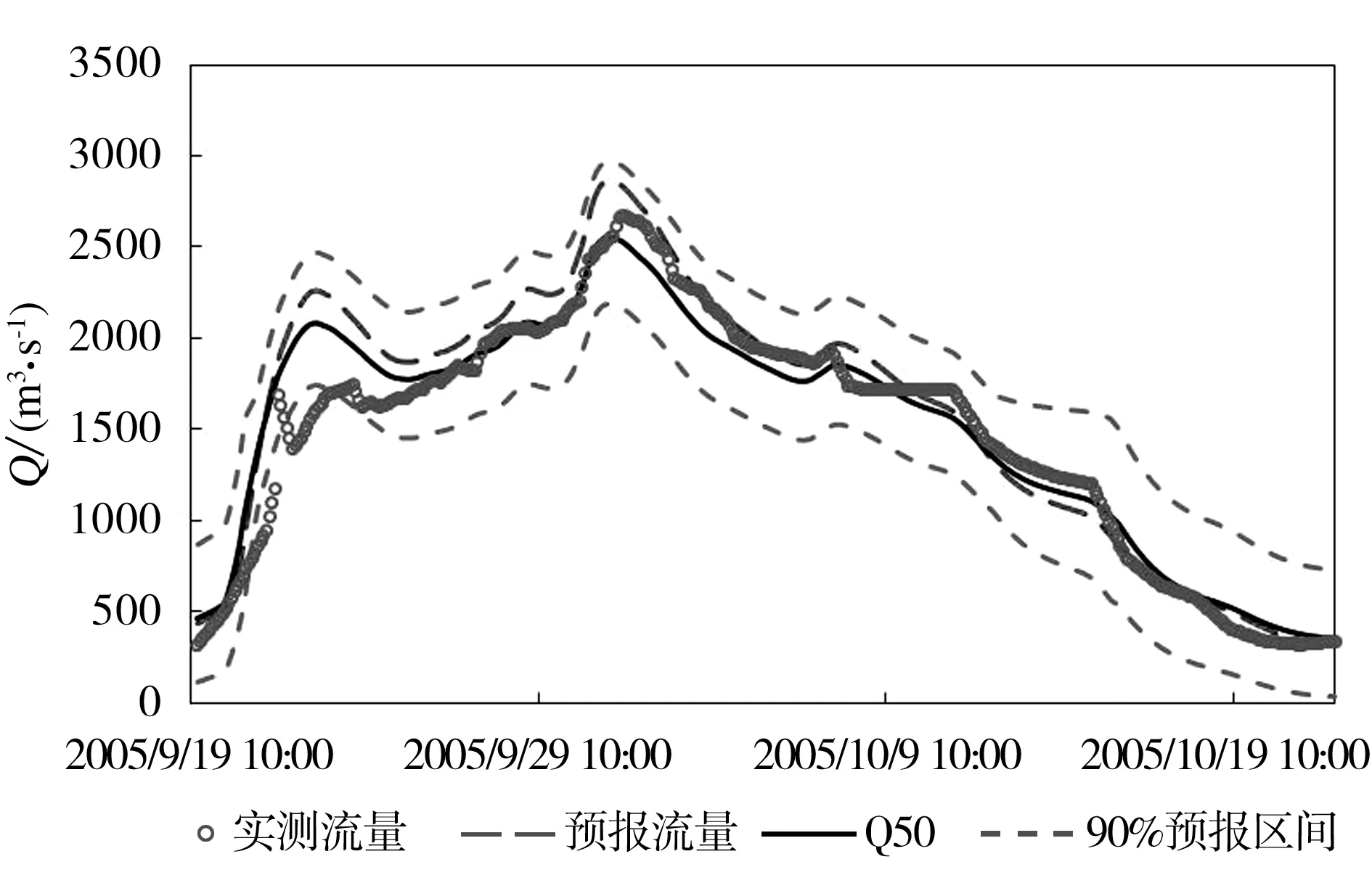
图4 20050919号洪水的概率预报结果

4 结 论

(1)分析了运河站洪水预报误差的均值和标准差与预报流量间的关系，发现洪水预报误差的均值和标注差与模型预报量间存在显著的分段线性关系，采用分段线性函数建立了预报误差的均值、预报流量和预报误差的标准差、预报流量间的描述关系。

(2)采用次洪径流深相对误差、洪峰相对误差及确定性系数3个指标， 评估了原始确定性模型预

表3 率定期和验证期洪水概率预报评估结果

表4 概率预报模型的Q50预报结果与新安江模型预报结果对比

报精度和误差异分布模型的中位数(Q50)预报精度。结果表明，经误差异分布模型处理后，洪水预报精度得到进一步的提高。

(3)基于覆盖率和离散度指标，评估了误差异分布模型计算的90%置信度预报区间对实测系列的覆盖率。结果表明，10场洪水的平均覆盖率达93.4%，平均离散度为1.2， 90%预报区间能覆盖绝大多数的实测数据。