地震荷载作用下的地铁车站变形缝动力响应分析
2020-09-12李贵仁
李贵仁
(昆明地铁建设管理有限公司,云南 昆明 650011)
0 引 言
随着地下结构数量的增多以及地震的频繁出现,地下结构易出现整齐的贯通裂缝、钢筋剪断、混凝土结构沿界面有差异沉降等现象[1]。而且地下结构受到地质条件和截面形式突变等因素的影响,需要设置变形缝。
目前,相关学者对结构物变形缝的结构力学行为和变形规律进行了大量研究,取得了丰硕的成果。周川等[2]将一维等效线性方法应用于地铁车站的抗震分析,证明了此方法得出的分析结果与实测数据吻合度较高。阎西康等[3]使用ABAQUS软件给钢框架结构建立有限元模型,将数值分析结果与试验结果对比,得出施工缝的存在对框架结构抗震性能有不利影响。魏春明等[4]对留施工缝柱和整浇柱进行了抗震性能试验,探究了施工缝对柱动力响应的影响。陈远峰等[5]对设置施工缝的整浇框架结构进行荷载作用下的试验,研究表明施工缝的存在对结构整体抗震性能的影响较大。徐永等[6]探究了隧道横通道变形缝在地基不均匀变形和地震影响下的力学行为规律。胡志平等[7]通过模型试验研究了马蹄形隧道斜穿地裂缝时的隧道整体结构和变形缝的变形特征。杜修力等[8]基于ABAQUS有限元软件,对大开地铁车站在不同方向地震动力作用下的结构和上覆土体的位移受力特征进行了数值分析。在静力荷载作用下,带有变形缝的框架结构的力学性能与整浇混凝土也具有很大差异[9-10]。从以上研究成果可知,变形缝与施工缝的存在对结构的抗震性能和受力变形都具有一定的影响,但是地下车站结构变形和受力的影响范围和程度不够明确,值得进一步研究。
针对地震作用下变形缝对地下车站结构动力的响应,基于有限元软件对车站结构建立三维模型,进行线性动力时程分析,研究了不同地震强度下地铁车站设置与取消变形缝时的车站结构位移体系变化规律及受力特征。
1 工程概况
以西安某地铁车站的结构形式和地质断面为原型,车站标准横断面采用两层三跨的混凝土框架结构,结构水平横向21.0 m,高12.9 m,上部车站高5.4 m,下部车站高7.5 m,顶板厚0.8 m,中板厚0.4 m,底板厚0.6 m。车站位置工程地质条件良好,顶面位于地下4.8 m,属于浅埋地下结构。按地层沉积年代、成因类型,将车站沿线地貌单元划分为人工堆积层(Q4ml)、全新世砂土(Q4al)、更新世黏土(Q3pl)和更新世砂土(Q3pl)。地质横断面如图1所示。
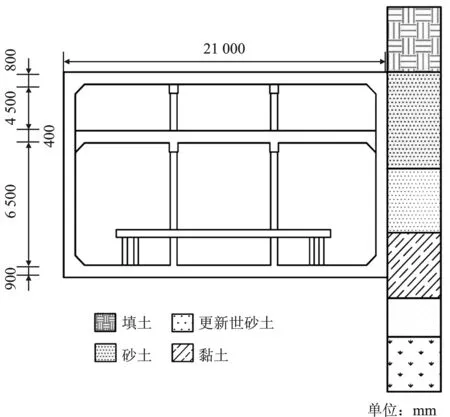
图1 地质横断面
根据规范规定变形缝间距,将地铁车站划分为5个区段,共4条变形缝。车站结构变形缝主要采用止水带连接,变形缝两侧发生差异沉降,会使止水带剪切变形。当止水带剪切应力大于止水带的剪切强度时,就会发生剪切破坏,如图2所示。

图2 止水带剪切变形
2 计算模型及参数确定
2.1 计算模型与边界条件

图3 有限元网格划分示意

图4 车站结构计算模型
本次有限元计算基于Midas-GTS软件进行数值模拟,本构模型和屈服准则分别采用理想弹塑性模型和摩尔-库伦准则。土体采用实体单元,车站外墙和底板采用板单元模拟,中柱采用梁单元[11],变形缝采用仅受拉弹簧模拟,模型如图3所示。计算区域两侧采用自由场边界,它的原理是采用黏滞阻尼器与自由场耦合来模拟动力边界[12],模型沿纵向长100.0 m,宽79.8 m,高31.2 m。本次数值模拟将物理性质近似的土层合并为4种土层。分别建立2种模型进行对比分析,一种是考虑变形缝影响的结构模型,另一种是不考虑变形缝影响的结构模型,如图4所示。其中X方向为车站轴线方向,Y方向为与隧道轴线竖向垂直方向,Z方向为与隧道轴线水平垂直方向。
2.2 模型材料参数
土体是地震波的传播媒介,其特性对设计地震动的显著影响已经是公认的事实。土的动剪切模量比和阻尼比是土动力非线性性能中最重要的2个参数。目前,动剪切模量比和阻尼比的取值都是源于大量试验数据得到的拟合曲线。由于缺少动力数据,两者与应变的关系基于参考文献和工程经验选取。模型计算参数如表1所示。图5为西安地区粉质砂土的模量比和阻尼比随剪应变变化的典型拟合曲线[13]。土体的动剪切模量比和阻尼比随应变变化具有良好的规律性:随着剪应变的增大,动剪切模量比逐渐变小,阻尼比不断增大。最大动剪切模量的值一般由现场测得的剪切波速代入式(1)确定。
(1)
式中:Gmax为最大动剪切模量;ρ为土体密度,νs为土体剪切波速。

表1 计算模型参数
对于混凝土衬砌材料,采用Drucker-Prager模型来描述[14]。
数值模拟中,采用界面弹簧进行施工缝的模拟,选取的施工缝物理力学参数与止水带相同。界面弹簧同时考虑切向剪切性能和法向拉压性能。法向受力性能由“拉压弹簧”描述,切向受力性能由“剪切弹簧”描述[15]。界面材料根据相邻单元的刚度和非线性参数计算。
法向刚度模量为
Kn=Eoed,i/tv
(2)
剪切刚度模量为
其中
式中:vi为界面泊松比,取值0.45;tv为虚拟厚度系数,一般取值范围为0.01~0.10,这里取0.05;Csoil为土壤黏聚力;Ci为折减后的土壤黏聚力;E为弹性模量;R为强度折减系数,这里取0.8。
2.3 地震动输入
西安位于中、强地震活动带,抗震设防烈度为8度,建筑场地类别为2级。自公元前2世纪至今,境内共发生4级或以上地震128次[16]。采用场地未来50年超越概率25%(小震)、10%(中震)和2%(大震)的地震动人工波,进行地铁车站结构地震下安全性分析,人工波持续32 s,时间间隔0.02 s,最大峰值加速度为2.0 m·s-2,位于12.5 s。人工合成的地震波加速度曲线如图6~8所示。不同地震强度的峰值速度和地震波波幅有所不同,小震地震动峰值加速度为1.6 m·s-2,中震地震动峰值加速度为1.8 m·s-2,大震地震动峰值加速度为2.0 m·s-2,地震强度越低,振动波幅越小。

图7 未来50年超越概率10%时的加速度时程曲线

图8 未来50年超越概率2%时的加速度时程曲线
地震动下,土体与结构一起运动,不考虑土体出现滑动、分离的现象;不考虑地下水的影响,即不考虑孔隙水压力的改变和地震下土体液化现象[17]。
3 计算结果及分析
3.1 变形缝相对位移
车站变形缝可以防止不均匀沉降对结构的破坏,缓解结构形式突变产生的应力集中[18]。为研究地震作用下车站变形缝的动力响应,先整理出变形缝两侧的相对位移时程曲线,如图9所示。在地震波作用下(与车站轴线垂直方向),车站变形缝相对位移峰值都比较大,相对位移值随时间先急剧增加,后趋于平缓。位移峰值集中在7.5 s左右,此时与地震波的峰值时刻相对应。随着地震强度的增加,变形缝两侧的差异沉降也随之增大。小震下,相对位移值总体较小,位移峰值为15 mm;中震和大震作用下,相对位移峰值分别达到50 mm和58 mm。

图9 相对位移时程曲线
3.2 车站顶点位移分析
车站结构的水平位移值是反映结构受力特征的重要指标,结构重要部位节点处的最大水平位移见表2,模型监测点如图10所示。

图10 模型监测点布置
不同强度的地震波的频谱特性差异引起的各顶点位移峰值区别较大,但是车站顶点位移水平大致相似。由表2可见,各顶点Y方向的位移比X、Z方向的位移大;X方向位移较小,说明变形缝错动变形量比拉压变形量大。随着地震强度的增加,结构顶点相对最大位移值随之递增,最大值为13.7 mm,位于S7顶点Y方向。顶点有无变形缝,对结构位移的影响有明显的差异;设置变形缝时,顶点各个方向的位移明显比无变形缝时更大。车站上部顶点各个方向的位移比下部顶点大,上部接头更易遭到地震破坏。
图11为大震作用下设置变形缝时监测点S1的相对位移时程曲线。监测点S1各个方向的相对位移总体表现为先逐渐增大,后减弱;Y方向前4 s位移较平缓,因为地震波加速度还未达到峰值,在5 s之后位移逐渐增加,在10 s处达到峰值,为11.2 mm;Z方向位移峰值接近6.4 mm;X方向位移峰值接近3.5 mm。

图11 监测点S1位移时程曲线
3.3 结构应力结果分析
由冯·米塞斯应力(图12)分析车站结构设置变形缝在地震作用下的应力特性,得出设置变形缝结构的受力特性与未设置变形缝结构相似。在地震波作用下,中板与边墙连接部位应力集中,侧墙下部墙角位置应力也较大,易出现受拉破坏。中柱与顶板连接部位易出现受压破坏。

图12 冯·米塞斯应力
不同地震动强度下车站顶板结构的最大主应力如图13所示。不同地震动强度源于模型中的人工波,人工合成的地震波加速度曲线如图6~8所示,不同地震强度的峰值速度和地震波波幅有所不同。未设置变形缝时,地震波作用下的应力分布近似于沿车站纵向呈凹形,应力峰值分别为2 250、2 020、1 490 kPa。在大震和中震下,应力值均大于混凝土轴心抗拉强度标准值,会出现裂纹,影响结构安全;在小震下,结构安全有保障。设置变形缝后,结构整体受力得到改善,应力值明显降低,大震、中震和小震作用下最大应力值与未设置变形缝时相比,分别减小13.5%、21.3%和40.2%。变形缝的存在提高了车站结构的柔性,使应力得到释放,提高了抗震能力,而且最大值均未超过混凝土抗拉强度标准值,满足结构安全性要求。

表2 测点位移 mm
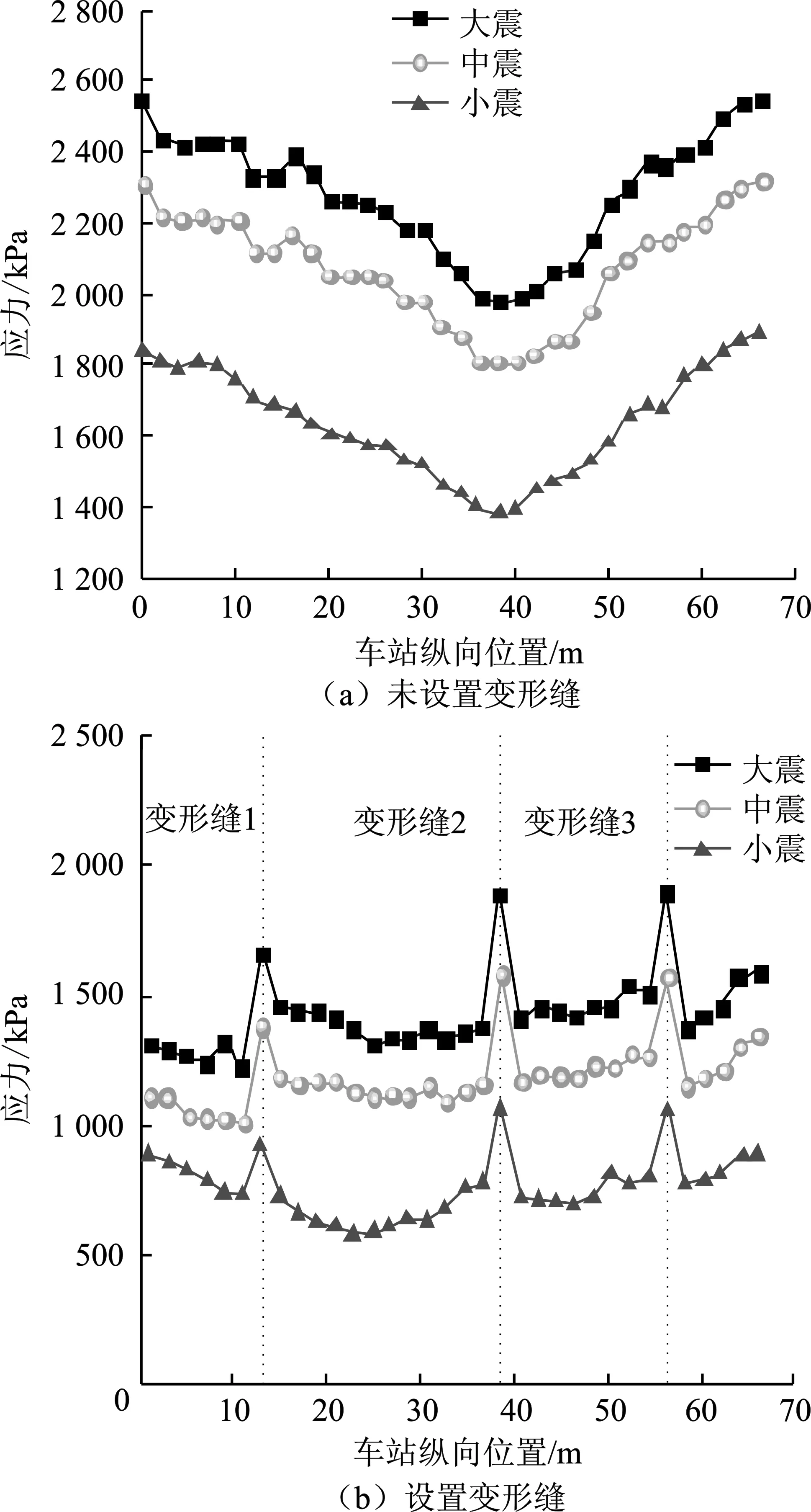
图13 沿车站纵向结构最大主应力
4 结 语
(1)在地震波作用下,车站变形缝相对位移峰值较大,相对位移值随时间先急剧增加,后趋于平缓。
(2)不同强度地震波的频谱特性差异引起的各顶点位移峰值区别较大,但是车站顶点位移水平大致相似。车站有无变形缝,对结构位移的影响有明显差异,设置变形缝时,顶点各个方向的位移明显比无变形缝时更大。车站上部顶点各个方向的位移比下部顶点大,上部接头更易遭到地震破坏。
(3)对结构纵向应力而言,变形缝的存在提高了车站结构的柔性,使应力得到释放,提高了抗震能力,而且最大值均未超过混凝土抗拉强度标准值,满足结构安全性要求。大震、中震和小震作用下,最大应力值与未设置变形缝时相比,分别减小13.5%、21.3%和40.2%。
(4)不同震级下,变形缝错动量均在允许范围之内,所以设计时可以允许有更大变形,更好地缓解应力集中的情况。
