基于时变摩擦系数的直齿轮副动态特性分析

蒋国凇

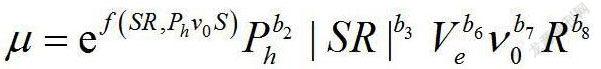
摘要：建立考虑时变摩擦系数的圆柱直齿轮啮合模型，讨论啮合过程单齿与双齿交替下的载荷突变下的时变直齿轮副摩擦因数变动规律。基于混合润滑模型分析了不同齿面粗糙度对应的时变摩擦系数，进而研究时变摩擦作用下齿面粗糙度对直齿轮副时变摩擦因数，动态啮合力，动态传递误差，振动速度变化的影响规律。研究结果表明，时变摩擦因数在单双齿交替啮合区发生突变并在节点处趋于0，节点后摩擦因数较节点前小，齿面时变摩擦系数受齿面粗糙度影响较大;齿面摩擦作为内部激励摩擦力对齿轮在啮合线方向的振动产生了一定情况的抑制，从而抑制了齿面动态传递误差的产生与动态啮合力的幅值，齿面表面速度所受影响较小。

关键词：直齿轮副;齿面摩擦;时变摩擦系数;动态啮合力

0  引言

齿轮表面时变摩擦力会促进齿轮根部裂纹产生与扩展开以及齿轮轮齿断裂[1]。齿面摩擦力作为齿轮传动内部激励之一，对系统的动态特性产生一定的影响[2-5]。因而，有必要从齿面微观变化为起点，深入讨论轮齿表面时变摩擦激励机理，研究时变齿面摩擦力对齿轮系统动力学特征的影响。

一对齿轮副在单双齿交替啮合中，齿面摩擦激励的大小幅值、方向都将发生周期性的变化，从而产生一种非谐波型的内部激励，使齿轮系统产生振东和噪声。江汉俊[6]研究考虑摩擦-振动相互作用的直齿圆柱齿轮的动力响应，建立了基于小齿轮扭转振动运动的时变啮合刚度函数。 Vaishya等[7-9]通过建立了齿轮表面摩擦单动力学模型，通过矩形波将时变刚度拟合，研究了齿轮副载荷分布、齿轮表面摩擦力。Velex等[10]基于库仑摩擦模型研究低速重载时齿面摩擦对齿轮系统的振动有重要影响。陆凤霞[11-12]建立了考虑时变摩擦和综合传递误差的直齿轮副6自由度弯曲-扭转耦合的非线性动力学模型。

在直齿轮副动力学特性分析中，建立考虑时变摩擦力摩擦的直齿轮副啮合模型，研究讨论啮合过程单齿与双齿交替下的载荷突变下的时变直齿轮副摩擦因数变动规律;分析时变摩擦作用下齿轮粗糙度、输入转矩等参数对直齿轮副动态啮合力的影响规律。研究成果有助于进一步认识时变摩擦激励对直齿轮副动力学特性的影响，为直齿轮副的设计分析提供了参考。

1  齿面的时变摩擦系数

齿面摩擦因数主要受轮齿表面粗糙度、表面硬度、轮齿单位法向载荷和齿面相对滑动速度等因数的影响。实验结果表明基于弹流润滑理论计算得到的摩擦因数与实际测得的摩擦因数更为接近，Xu[13]认为目前的滑动摩擦因数计算公式得出的结果一般较大;齿面啮合趋近与节线时，时变齿面摩擦因数近似于0;齿面啮合点的滑动速度和卷吸速度之比的绝对值越小，滑动摩擦因数越小。

为更加真实模拟齿轮副表面摩擦工况，本文即采用该摩擦因数计算模型计算时变摩擦系数，讨论时变摩擦力对于直齿轮副的动态传递误差，动态啮合力，相对速度的影响规律，基于弹流润滑润滑理论的摩擦因数计算模型为：

为算例，讨论轮齿表面时变摩擦因数变化情况。齿轮几何参数与工况为：z1 =16 z2=24;=20°;m=4.5mm齿宽 b=20mm; ha*=1; E=210GPa;ν=0.3;S=1.6μm;n=1000 r/min;T=20N·m; bc=100μm;阻尼比为0.1。

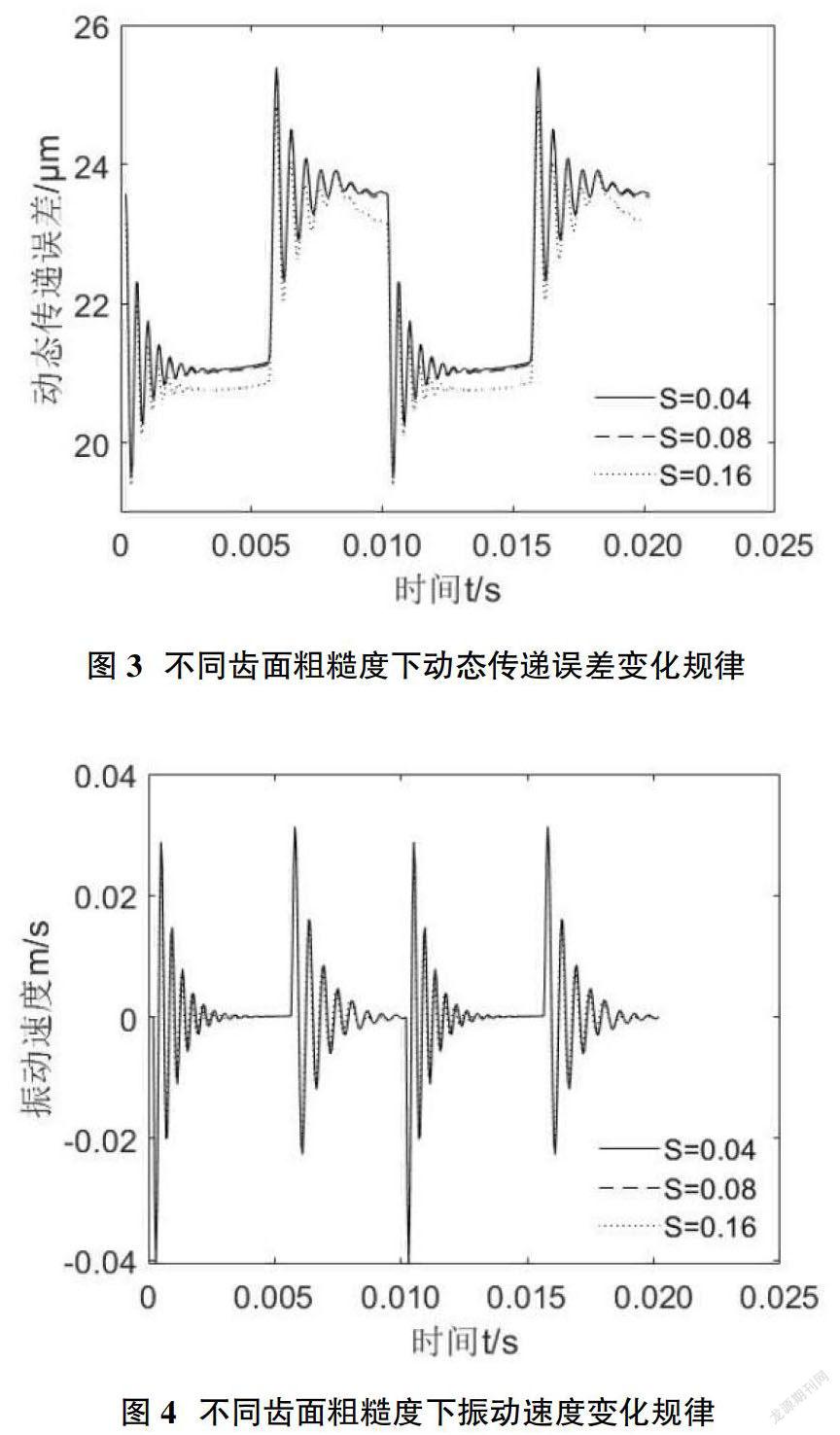
图1至图4给出了不同齿面粗糙度下的动态特性结果。根据图1可以看到，表面粗糙度的大小对时变摩擦因数影响较大，随着表面粗糙度的增大，时变摩擦因数明显变大，曲线变化趋势由平缓向陡峭转变。在齿轮表面加工过程中，我们应该合理选择切削速度、合理选择进给量、合理选择刀具几何参数、可以采用增加相应工艺的办法降低齿轮表面粗糙度，从未降低齿面摩擦对齿轮副运动的影响。由于面粗糙度的增大影响时变摩擦因数，从而使齿面表面摩擦力增大，齿轮副表面摩擦力作为内部激励抑制动态啮合力与动态传递误差。一方面说明当摩擦力作用力矩与驱动力矩反向时，摩擦力在一定程度上抑制了齿轮在啮合线方向的振动，进而减小了动态误差的产生与动态嚙合力的幅值。振动速度的变化规律与前面动态特性结果不一致，表明齿面速度变化规律受齿面摩擦力的影响较小，几乎可以粗略不计。

2  结论

①建立考虑时变摩擦系数的圆柱直齿轮啮合模型，研究啮合过程单齿与双齿交替下的载荷突变下的时变直齿轮副摩擦因数变动规律。

②时变摩擦系数在齿面啮合过程中因载荷分配发生突变;在啮合点趋于节点处，时变摩擦因数趋于0;摩擦力作用下时变摩擦因数啮入阶段较大，啮出阶段较小。

③不同齿面粗糙度下时变摩擦因数随着齿面粗糙度的增大而增大，摩擦力作用力矩与驱动力矩反向时，摩擦力在一定程度上抑制了齿轮在啮合线方向的振动，从而制动态啮合力与动态传递误差，振动速度的变化规律与前面动态特性结果不一致，表明齿面速度变化规律不受齿面摩擦力的影响。

参考文献：

[1]Flasker J，Fajdiga G，Glodez S，et al. Numerical simulation of surface pitting due to contact loading[J]. International Journal of Fatigue，2001， 23（7） ：599 -605.

[2]He S，Gunda R，Singh R. Effect of sliding friction on the dynamics of spur gear pair with realistic time-varying stiffness [J]. Journal of Sound and Vibration，2007， 301（3-5）： 927 -949.

[3]Velex P，Sainsot P. An analytical study of tooth friction excitations in errorless spur and helical gears[ J] . Mechanism and Machine Theory，2002， 37（ 7） ：641 -658.

[4]He S，Singh R，Pavic G. Effect of sliding friction on gear noise based on a refined vibro-acoustic formulation[J]. Noise Control Engineering Journal，2008， 56（3）：164 -175.

[5]Velex P， Cahouet V. Experimental and numerical investigations on the influence of tooth friction in spur and helical gear dynamics[J]. Journal of Mechanical Design， 2000， 122（ 4） ：515 -522.

[6]Jiang H ， Liu F . Dynamic modeling and analysis of spur gears considering friction–vibration interactions[J]. Journal of the Brazilian Society of Mechanical Sciences and Engineering， 2017， 39（18）：4911-4920.

[7]Vaishya M，Singh R. Strategies for modeling friction in gear dynamics[J]. ASME Journal of Mechanical Design，2003， 125： 383 -393.

[8]Vaishya M，Singh R. Analysis of periodically varying gear mesh systems with coulomb friction using floquet theory[J]. Journal of Sound and Vibration，2001，243（3）：525 -545.

[9]Vaishya M，Singh R. Sliding frictioninduced nonlinearity and parametric effects in gear dynamics[J]. Journal of Sound and Vibration，2001，248（4）：671 -694.

[10]Velex P，Sainsot P. An analytical study of tooth friction excitations in spur and helical gears[J]. Mechanism and Machine Theory，2002，37（7）：641 -648.

[11]陸凤霞，王浩飞，朱如鹏，鲍和云，姜慧卉.基于齿面摩擦的人字齿轮副动力学特性分析[J].振动与冲击，2016，35（09）：204-212.

[12]陆凤霞，王浩飞，朱如鹏，鲍和云，姜慧卉.基于齿面摩擦的直齿轮副动力学特性分析[J].机械传动，2015，39（11）：27-32.

[13]Xu H， Kahraman A， Anderson N. Development of a generalized mechanical efficiency prediction methodology for gear pairs[D]. Journal of Mechanical Design， 2005.