基于OAM拓扑模式复用的水声通信技术进展

李晖 徐洁 王厚 李千 石崇岳

摘 要：将轨道角动量（OAM）理论引入水声通信中来，利用不同拓扑模式螺旋声波内在正交性，构建基于OAM拓扑模式复用（TCM）的多入多出（MIMO）水声系统，获得更高信道容量和频谱效率。理论上拓扑模式可以无限制的增大、即模式复用的次数没有限制，基于此复用的MIMO系统将获得更高的频谱利用率。本文概述了浅海和深海水声信道的差异，描述了水声OAM-MIMO技术的现状和发展情况，并提出了未来可能遇到的技术挑战和问题。OAM-TCM在水声通信的应用前景令人兴奋，即存在机遇、也面临巨大的技术风险。

关键词：水声通信，MIMO，螺旋声波，轨道角动量，拓扑模式复用

一、引言

21世纪初，世界各个海洋国家围绕海权的争端不断加剧，海洋科学与技术的发展具有极大的活力和广阔的前景，成为当前的热点科学技术之一。近年来，鉴于海洋油气等水下资源勘探的需要、以及沿岸有限战争概念的提出，并伴随着我国海洋开发活动的增加和海上丝绸之路的不断延伸，水声通信在国计民生和军事活动中占据越来越重要的地位。

有学者将MIMO技术引入水声通信中来，利用声波在水声信道中的多径/多途传播特性来实现高速、可靠、多用户通信[1]。有学者开展了基于轨道角动量（OAM，Orbit Angular Momentum）多路复用的陆上实验，验证声波螺旋信号高效传输理论上的可行性[2];其将OAM螺旋波束复用与MIMO技术相结合，构建基于螺旋声波换能器阵列的通信系统，为水声通信速率低的难题提供了新的解决途径。

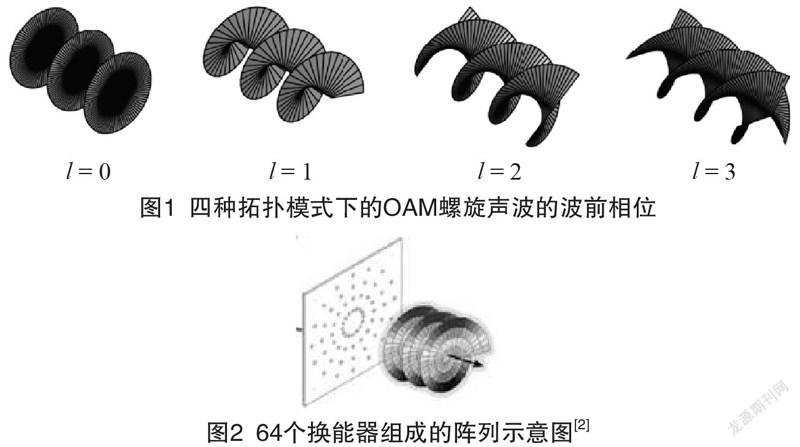
图1中，OAM的四种拓扑模式的声波，对应MIMO通信的四个正交信道，发射端按照一定构型组成发射换能器阵列，同时产生多个拓扑模式的螺旋声波，如图2所示，接收端采用相类似的阵列结构。理论上四种拓扑模式（l = 0，1，2，3）之间的正交性决定了可以将信息速率提升四倍。

因此揭示基于OAM的水声通信高速传输机理，研究OAM-MIMO声波复用信号的水下传播特性与抗串扰方法，特别是开展针对浅海海域“波—流—湍流”耦合作用、考虑多路径传播、多普勒频移的水声OAM阵列信号产生、分离和处理方法的研究，在民用和军事领域都具有重要意义和广阔的应用前景[3-6]。

二、OAM技术在水声通信中应用

（一）OAM声波螺旋的产生

无论是在光学领域还是无线电领域，OAM都表征了螺旋相位结构波形的自然属性;通过引入OAM，通信系统的传输能力将得到扩展[7]。携带OAM的声波波束，其螺旋相位取决于OAM拓扑模式，理论上不同的拓扑模式的波在空间上正交，在提供了一种与能量、波长和极化方式为一样的新的自由度[8]，构成一种新的复用机制。

对于空气中的光波和微波，不同拓扑模式螺旋波束的产生方式很多，包括空间光调制器、透射螺旋结构、透射光栅结构、超表面、螺旋反射面、天线阵列、分时对称环形谐振腔等[7，8]，并通过波束分离器或自旋轨道耦合完成波束复用，以达到增加数据传输速率的目的，这些方法为螺旋声波的产生提供了借鉴。螺旋透射结构一般应用于光学领域，并且工作在较高频段的毫米波。螺旋相位板通常使用单阶，多阶以及多孔状螺旋相位结构，在实际操作中较多使用多阶梯螺旋相位板。

透射光栅结构的具体产生方法包括基于叉形光栅，基于达曼涡旋光栅叠加涡旋光束，基于Lin算法的多模式，透射光栅结构一般多使用计算全息方法。螺旋反射面产生轨道角動量的方法包括阶梯型反射面和扭曲抛物反射面。螺旋反射面一般应用于低频段，当波束入射螺旋反射面时，不同区域的波束出现不同的相位延迟，经过巧妙地设计即可让反射波束的波前发生扭曲形成涡旋波束。

环形行波分为环形金属腔和环形槽线。行波天线模型一般采用偶极子天线，偶极子尺寸较小，通过将天线弯曲成圆环，然后对天线进行馈电。馈电电流强度沿环保持恒定，而相位沿环连续变换。电磁超表面材料通过计算每个单元需要改变的相移，设计反射单元尺寸，通过尺寸分布可以的得到反射超表面的拓扑结构。透射型电磁超表面可以同时独立调控电磁波的幅度与相位的特性，可以将球面波变换为涡旋波束。反射阵列天线通过调节阵列单元结构可以调节反射波的相位变化，使得反射波束具有任意的相位波前，根据反射阵单元的相移特性可以很方便地构造螺旋的相位波前结构，形成OAM波束。

天线阵列产生轨道角动量的方法包括，圆形相控阵，巴特勒矩阵馈电网络天线阵和光延时单元天线阵。对于按照一定顺序排列的天线阵列，依次对其馈送相同但相位依次延迟的信号，能够使得发射的电磁波带有轨道角动量。对空间上呈一定分布的天线使用相同馈电，利用空间分布的不同来产生相位延迟，也能够产生轨道角动量波束。

阵列天线产生OAM波束实际就是利用连续相位延迟激励阵列上的不同阵元，产生涡旋电磁波。一般应用在低频段，并且能做到轻量化和小型化，因此，阵列天线特别是圆形相控阵列天线的是目前最常用且常用的OAM波束产生方式，也会有很大的应用场景。

OAM波束的检测方式一般有单点法和相位梯度法。单点法是使用OAM远场近似从电场估计磁场，可以通过计算空间中每个点上波束的特定OAM模式数。相位梯度法是显式地利用螺旋相位结构，通过测量相位梯度来计算OAM模式，通过在XY平面上用两点相位测量来近似相位梯度。

产生声涡旋OAM的方式一般分为两大类，有源和无源。有源技术属于声学相控技术，原理是通过对声学换能器的独立调控来形成相控阵列，产生能够形成螺旋状的相位分布。声学OAM的有源产生方法需要昂贵的成本和复杂的电路，在高频段应用有一定的困难。

无源材料产生声学OAM相对有源材料来讲，方法更加简单。Gspan等人通过在水槽中用脉冲激光来照射具有特殊结构的吸声材料表面，利用材料受热后产生的热弹效应激发向另一侧传播的压力波[9]。Ealo等人提出了利用多孔铁电驻极体材料在空气中产生涡旋声场的理论方法，并在实验上加以实现[10]。基于超表面材料也可以产生声学涡旋，刘正猷课题组提出了利用尺度小于波长的超表面将平面波转化为带有OAM的涡旋声束。梁彬等人提出了利用超构表面在声学体系中引入OAM[11]。

（二）水声通信中应用OAM技术

学者将OAM应用于水下光学通信中[12-14]，也有学者研究如何将OAM多路复用声波应用于水下声学通信中[2]。Shi等为实现数据高速传输利用新的自由度——载波的OAM，以增加水声通信的容量——并行传输速率随着拓扑模式成倍增加，增加的容量来源于同一频段内可用带宽和模式数量之积。一般而言，模式复用和现有的调制技术结合——如PSK（Phase Shift Keying）、QAM（Quadrature Amplitude Modulation），将会提升水下通信速率为原来的L倍，其中L为OAM拓扑模式数量。对于水声通信而言，水下OAM声波的产生、传播和接收是OAM技术应用过程中的关键问题。

实际水声通信场景中，OAM模式复用会遇到巨大的挑战，OAM声波的产生方式不同造成声波能量效率的巨大差别（例如，反射式OAM的螺旋相位板与馈源同轴，造成轴向附近波的遮挡），接收端和发射端的轴向非对齐造成的声波接收困难、能量发散，并破坏不同拓扑模式之间的正交性;浅海普遍存在的中尺度湍流、盐度、温度、浊度（地表径流注入）的跃变造成OAM声波的折射和反射效应凸显;以及多普勒的频移、不同OAM模态下MIMO信道状态估计、信道均衡、相位失真和多种海洋噪声影响。

OAM声波具有四个主要特性：沿传播轴方向场强为零、相位在[0，±2lπ]内分布、传输过程中的波形自我修正能力、以及将力矩传递给物质使其旋转。本项目中利用了OAM声波的前三个特性，OAM螺旋声波复用的关键，首先是产生螺旋波束，拓扑模式数l = {0，1，2，3}。在柱坐标系（ρ，φ，z）下拉盖尔—高斯（L-G，Laguerre-Gauss）型螺旋波束的场分布一般表示为：

式中ρ、φ、z、k、l和p分别为到辐射轴的辐射距离、方位角、传播距离、波矢量k = 2π/λ、拓扑模式数和径向节点数，代表z处的波束宽度（如ω0代表z = 0处的波束半径）、ω0为束腰半径、表示Rayleigh距离、λ为波长，代表一般Laguerre多项式;此外，如果分配给每一种拓扑模式相同的能量，则系数，A为总辐射能量。

OAM螺旋波束具有内在的正交特性，即两个OAM电场幅度的标量积为：

上式说明对于任意两个不同模式（l1 ≠ l2）的OAM波束和，当p为固定值时、理论上两者的相关度为0，即满足相互正交特性;文献2的实验中8种拓扑模式间的串扰小于-8.54 dB;在理论上OAM复用随着模式数的增加具有无限的传输能力。但是Shi等仅在陆地声波传输环境中进行了理想仿真和实验[2]，而实际当中的水下测试需要考虑更为复杂的因素。

在以往的研究中，通常采用大数模阵换能器阵列来产生具有不同函数的特定声场，如L-G型和贝塞尔函数型。对贝塞尔型OAM波束具有的依赖性方位角，在柱坐标下场分布的表达式如（1）中所示。同时，天线阵列产生的波束一般为贝塞尔函数型波束，也具有依赖性，阵列因子表示为，电场表示

随着OAM拓扑模式数l增大，主瓣夹角变宽，即最大增益的方向角变宽。有学者已经仿真验证过，当阵列单元数N = 12时产生的四种OAM模式下辐射模型，OAM模式数l = 1时，主瓣夹角较小，约为60°，随着模式数l的增大，主瓣夹角逐渐增大。当l = 4时，主瓣夹角约为120°。

通过对阵列半径和激勵信号幅度的设计，可以有效控制不同OAM模式的强度分布，同时无需改变相位角分布。从的公式中可以得出，通过对阵列半径的设计，可以将不同模数的涡旋波束的主瓣准直到相同的仰角方向。通过增大阵列的直径或者增大各单元的方向性，可以减小沿轴方向的空隙宽度，即减小增益角度。通过增加阵列直径，虽然在减小增益角度的同时，旁瓣的数目有所增加，同时能量有一部分的损失，但增加的旁瓣角度比主瓣宽很多，并且旁瓣增益也比主瓣弱很多，所以产生的影响在实际检测过程中并不重要[15]。

Hefner等利用L-G波的零点指明波束主轴方向的特性，利用L-G波研发了一个水下换能器，用于校准水下超声波方向或其他水下应用（例如将多个物体沿着同一个轴布设）[16]。虽然这仍是利用了OAM对颗粒的捕获和操纵的能力，但首次证明了产生水下螺旋声波的可能性，为水声学OAM的研究打开了窗口。

Brunet等在水箱中针对模式l = +1和l = +3的两种OAM超声波进行了检测。利用127个压电换能器构成球型聚焦阵列，换能器阵列的平面投影为正六角形，每一个换能器输出波的幅度和相位独立驱动，超声波的频率800 kHz。在距离发射阵列Z轴500 mm处，利用水听器对超声波场强进行采样，采样范围40×40 mm，每隔0.5 mm进行采样，共计81×81 = 6561个样本，采样频率625 MHz，在每一点采样32次并做均值处理[17]。实验验证了水下多模式OAM波的产生和远场传播的可行性，为后续OAM阵列声波产生和接收指明了方向。

同时，学者们提出了多种产生螺旋声波的方法，如Jiang等利用谐振腔将普通声波转换为OAM声波[18]，Ye等利用一种超平面结构（四个共振腔环形分布在亚克力板上）产生声学螺旋波[19]，Naify等利用超材料缝隙天线产生声学螺旋波[20]，Jiang等利用多臂螺旋裂隙板产生声学螺旋波[21]，以及利用尺度小于波长的超表面将平面波转化为带有OAM的涡旋声束，或者利用超构表面对声学体系引入OAM。这些方法为水下声学螺旋波的低成本产生方法提供了借鉴。

2017年6月，劳伦斯·伯克利国家实验室首次完成了螺旋声波多路复用的陆上试验，载波频率16 kHz;采用4×16个换能器构成换能器阵列，利用数控电路控制OAM波前、形成8个正交信道，实现通信速率8倍的提升[2];34或者68个换能器组成接收阵列、接收和测量声波，得到的BER分别为2.0×10-3和1.0×10-5.3。但其陆上试验的收发距离仅为100个波长、即2.125 m的距离，还不足以完全验证其水下传输的有效性，其方案适用性和系统可靠性也有待验证。

（三）OAM拓扑模式复用

基于OAM的拓扑模式（TCM，Topological Charges Multiplexing）复用技术可以看成是一种特殊的基于拓扑模式空间的MIMO复用技术[22]，其实现方式与传统的MIMO技术有很大的不同，体现了OAM复用的技术优势[8，22]。针对OAM复用理论，Wang等设计并演示了基于OAM拓扑模式的新型光复用通信系统，通过多个分束器实现不同OAM拓扑模式的复用[23]。Thide首次提出将光子OAM应用于低频，验证了相控阵天线产生L-G螺旋电磁波，开创了OAM无线电应用的先河，提出了利用螺旋电磁波增大无线通信系统容量的设想[24]。Tamburini等利用修正的抛物面天线产生螺旋波束，首次在微波频段实现了OAM复用[25]。

理论上OAM-TCM系统的通信容量随着复用OAM拓扑模式数线性增加，且不增加接收复杂度。此外，OAM复用技术不依赖于传统的复用方式，所以能有效地与其他复用方法相结合，包括时分复用、极化复用和频分复用，以便进一步提高系统的信息传输速率。

传统MIMO系统通常存在子信道间干扰，接收端采用信道均衡算法来消除这种串扰，往往能有效地恢复发射的信号;而在OAM-TCM系统中，信息的复用和解复用都是通过OAM波的发射—接收系统自身实现的，在理论上不存在子信道间串扰[26]。所以，OAM这一螺旋调制维度不仅能给无线通信系统带来复用增益、也大大降低了信息解复用的接收复杂度，从而简化基带电路的设计、降低系统能耗。

国内已经出现在水声通信领域、将OAM声波复用与MIMO结合起来的研究成果，产生单模式螺旋声波[27];但更多的还是将OAM应用在水下光学链路中[12-14]。本项目可以借鉴自由空间、大气和海洋背景下OAM光学和电磁学复用的多项研究成果，并加以改进和完善，以完成水声学领域的基于OAM拓扑模式的复用技术研究。

OAM拓扑模式描述了一种空间相位分布，因此基于OAM拓扑模式复用的水声通信系统将不可避免地受到海水信道快速变化的影响，其中湍流是造成水声信道快速变化的主要因素[28]。湍流不但影响了单路OAM声波相位，还导致多路OAM-TCM信道间的串扰，对MIMO信道正交性、以及接收信号的分离造成极大困难。

（四）相位校正

OAM声波的传输要考虑声波从发送端到接收端吸收衰减、多途传播、多普勒效应、以及聲波的时变性、环境噪声等影响[29-30]，而这些干扰通常主要是由海洋湍流所引起的。目前主要研究干扰抑制方法是针对大气湍流和OAM自由空间光通信系统而言[31-34]。波前校正抑制方法可以有效降低大气湍流引起的串扰效应，对OAM光波前相位失真具有很好的抑制效果。

针对光学OAM系统的相位校正技术主要针对大气湍流干扰，例如有学者利用LDPC（Low Density Parity Check）纠错码抑制大气湍流对OAM模式复用的影响[35，36]，有学者利用双路自适应Shack-Hartmann波前校正技术对大气湍流引起的OAM模式复用干扰进行校正，也有学者利用MIMO自适应均衡方法降低大气湍流导致的OAM模式复用信号串扰，采用基于光强Zernike多项式的随机并行梯度下降算法[37]，来校正大气湍流的影响。

常规的Shack-Hartmann（SH）波前传感技术依靠接收光束各部分之间的强度差来计算畸变，不能很容易地用于重建OAM光束的螺旋相位。自适应光学SH波前校正方法是基于SH波前抑制方法的改进，单路自适应SH波前校正技术是一种前向校正方法，OAM复用光到达接受端前经过一个自适应SH波前校正器进行OAM复用光波波前相位误差校正[38]。双路自适应SH波前校正对接受端OAM复合光信号进行补偿的同时也可以对发送端的信号进行预补偿，相比于单路自适应光学SH波前校正技术，效率明显提高，校正效果更为明显[39]。另外还有一种将带有数据的高斯光与OAM复用信号合束后同轴传输，经过大气湍流后再在接收端分离光束，利用SH波前探测器探测高斯光束的畸变，从而得到相应的涡旋光束波前畸变相位。这种方法利用偏振高斯光束探测湍流，结果可以同时校正高斯光束和OAM光束[40]。

除此之外，一种基于 Zernike 多项式的随机并行梯度下降算法，也能有效的校正OAM复用系统畸变相位。该校正算法不需要波前探测器，与上述校正算法相比，系统结构更加简单，收敛速度和校正效果更好，而且应用环境更广泛[41]。Gerchberg-Saxton算法（GS算法）也不需要波前探测器，该算法利用物空间和像空间的傅里叶变换和逆变换交替，将光强信息转变为相位信息，用失真的OAM态复用光幅度谱作为相位校正因子，通过迭代算法得到变形相位，继而校正相位[42]。最近有学者将GS算法与CNN（Convolutional Neural Network）模型结合来校正湍流环境下的复用OAM波束。该技术用GS算法对OAM波束进行一个初始的相位校正后，再用CNN算法对不同拓扑模式和径向指数的复用OAM光束进行分类，可以获得更好的校正效果[43]。

20世纪80年代开始有学者将部分湍流模型应用于海洋，这些湍流模型大多是由空气动力学和流体力学领域继承而来，并针对海洋环境的问题作出调整。大多数海洋模型使用单方程或双方程模型，其中Mellor-Yamada Level 2.5封闭模型和k-ε模型应用较为广泛[44]。Smith等人用k-方程模型和k-ε模型模拟了河口潮流的垂直结构[45]。Svensson在湖泊里使用了浮力扩展的k-ε模型来对垂直结构进行了建模[46]。Burchard和Baumert开发了一个k-ε模型，并对其局部稳定性进行了代数校正[47]。Bloom R等人将k-ε模型和两方程形式的Mellor-Yamada（M-Y）模型分别应用在对北海上层和下层混合层，结果表明了这两个模式的相似性，并且证明了k-ε模型可以比M-Y模型更好地再现湍流剖面的测量结果[48]。Katie L等从波浪-湍流的角度研究了双层海洋模型[49]。赵生妹等用基于功率谱反演法的随机相位屏模型来模拟海洋湍流对OAM光束的影响[50]。

但是相对于大气湍流来说，对水下湍流模型的应用和相关研究仍然较少，而相应的对大气湍流的研究和相关技术都较为成熟。对于水下湍流模型的研究仍然可以参考大气湍流模型的相关理论，并根据水下湍流的适用性给出一定的修正。

针对海洋湍流，人们往往更关注OAM光束在海洋中传输时湍流对其传输特性的影响，如有学者推导OAM光束在海洋湍流中传输的交叉谱密度矩阵的表达式，数值模拟了OAM光束的光谱密度、光谱相干度、光谱偏振度等传输特性;有学者运用Rytov近似理论计算了海洋湍流对L-G光束携带OAM模式传输的影响，得到单模式OAM光束在海洋湍流情况下传输时的探测概率分布，并计算了海洋湍流下贝塞尔-高斯（B-G，Bessel-Gauss）光束的OAM通信系统的信道容量。

目前，针对水声OAM声波的相位校正工作，可以查找的文献极少，将大气/海洋湍流对光学OAM影响的研究成果平移到水声OAM中是否可行，还有待分析。但从中可以发现，有效的海洋湍流模式是分析OAM声波波束在海水中传输性能的关键;海水湍流对OAM声波传输中相位失真和符号间串扰有巨大影响;针对海水湍流的OAM螺旋声波校正方法还有待探索。

海水的切变和相变、以及两种不同粘滞性水体的混合、海水中溶解的镁盐、硼盐的分子弛豫现象、水下生物、气泡群，都会吸收声波的部分能量（吸收系数在一定频率范围内与频率的平方成正比），造成OAM声波能量损耗，严重时造成接收端判决错误。由于湍流的随机性、易变性等特点，一方面一直难以找到合适的方法抑制它的影响，另一方面浅海湍流存在的普遍性、使得必须对OAM声波波前进行校正，以恢复扭曲相位信息。

三、结束语

现有理论研究和初步试验结果表明，OAM拓扑模式复用可应用于水声通信，可极大地提升水声通信系统的容量和频带利用率，理论上可行。但是，其实用化存在一些问题，如OAM产生成本、收发两端不对称接收问题、波—流—湍流耦合作用下的相位校正问题，以及OAM声场不同尺度下的水声信道匹配问题，这些都给OAM-TCM在水声通信中的应用带来极大的挑战。

建议综合考虑不同拓扑模式OAM螺旋声波的高效、可控和低成本产生方法，利用OAM拓扑模式的正交性承载不同信道的信息、以及OAM声波的空间圆对称性，构建发射/接收声波阵列和系统实现，同时对于调制在OAM螺旋声波上的信息，进行有效的检测和分离。由于OAM声波的特殊螺旋相位波前结构，在声波传播过程中，容易受到信道环境的影响如海水温度、深度、洋流、季節、温层等，破坏了波前相位的时空结构，使得不同拓扑模式之间的信息产生串扰。作为信息载体，需要开展针对螺旋声波的激励信号形式、调制/解调方式、信道复用/解复用、串/并转换、编码/解码，以及开展接收端信道均衡和波前校正等方面的研究。

揭示基于OAM的水声通信高速传输机理，研究OAM-MIMO声波复用信号的水下传播特性与抗串扰方法，特别是开展针对海洋“波—流—湍流”耦合作用下、多路径传播、多普勒频移的水声OAM信号产生、分离和处理方法的研究，提高水声通信的传输速率和频谱利用率，它在民用和军事宽带水声通信领域具有重要意义和广阔的应用前景。

参考文献：

[1]K. Pelekanakis， A. B. Baggeroer. Exploiting space-time-frequency diversity with MIMO- OFDM for underwater acoustic communications[J]. IEEE Journal of Oceanic Engineering， 2011，36 （4）：502-513.

[2]C. Z. Shi， M. Dubois， Y. Wang， X. Zhang. High-speed acoustic communication by multiplexing orbit angular momentum[J]. Proceedings of the National Academy of Sciences， 2017，144（28）：7250-7253.

[3]朱敏，武岩波.水声通信技术进展[J].中国科学院院刊， 2019，34（3）：288-296.

[4]李宏升，岳军，金久才，陈冰泉，邓剑平，高洪秀，刘尊年，孙志坚.蓝绿激光水下通信技术综述[J].遥测遥控， 2015，36（5）：16-22.

[5]H. H. Zhu， S. C. Piao， H. G. Zhang， W. Liu. Waveguide invariant estimation in elastic Pekeris waveguide[J]. Chinese Journal of Acoustic， 2017， 36（1）：113-129.

[6]杨坤德，李辉，段睿.深海声传播信道和目标被动定位研究现状[J].中国科学院院刊， 2019，34 （3）：314-320.

[7]孙学宏，李强，庞丹旭，曾志民.轨道角动量在无线通信中的研究新进展综述[J].电子学报.2015，43（11）：2305-2314.

[8]赵生妹，蒋欣成，巩龙延，程维文，郑宝玉.轨道角动量态复用通信研究[J].南京邮电大学学报， 2015，35（6）：1-13.

[9]S. Gspan， A. Meyer， S. Bernet， M. R. Marte. Optoacoustic generation of a helicoidal ultrasonic beam[J]. Journal of the Acoustical Society of America， 2004，115（3）：1142-1146.

[10]J. L. Ealo， J. C. Prieto， F. Seco. Airborne ultrasonic vortex generation using flexible ferroelectrets[J]. IEEE Transactions on Ultrasonics Ferroelectrics & Frequency Control， 2011， 58（8）：1651.

[11]梁彬，程建春.声波的“漩涡”——声学轨道角动量的产生、操控与应用[J].物理， 2017，46（10）： 658-668.

[12]A. D. Wang， L. Zhu， Y. F. Zhao， S. H. Li， W. C. Lv， J. Xu， J. Wang. Experimental demonstration of a feedback-assisted orbited angular momentum-based underwater wireless optical link across the underwater-to-air interface[C]. 16th International Conference on Optical Communications and Networks. Wuzhen， China， Aug， 7-10， 2017：1-3.

[13]K. S. Morgan， E. G. Johnson. B. M. Cochenour. Attenuation of beams with orbit angular momentum for underwater communication system[C]. IEEE OCEANS-MTS. Washington， USA， Oct. 19-22， 2015： 1-3.

[14]L. Li， Y. X. Ren， Y. W. Cao， et al. CMA equalization for a 2 Gb/s orbit angular momentum multiplexed optical underwater link through thermally induced refractive index inhomogeneity[C]. 2016 Conference on Lasers and Electro-Optics. San Jose， USA， June 5-10， 2016：1-2.

[15]S. M. Mohammadi， L. K. S. Daldorff， K. Forozesh， B. Thidé， J. E. S. Bergman， B. Isham， R. Karlsson， T. D. Carozzi. Orbital angular momentum in radio： Measurement methods[J]. Radio Science， 2010，45（4）：1-14.

[16]B. T. Hefner， P. L. Marston. An acoustical helicoidal wave transducer with applications for the alignment of ultrasonic and underwater system[J]. Journal of the Acoustical Society of America， 1999，106（6）：3313-3316.

[17]T. Brunet， J. L. Thomas， R. Marchiano， F. Coulouvrat. Experimental of observation of azimuthal shock waves on nonlinear acoustical vortices[J]. New Journal of Physics， 2009，11： 013002.

[18]X. Jiang， Y. Li， B. Liang， J. C. Cheng， L. K. Zhang. Convert acoustic resonances to orbit angular momentum[J]. Physical Review Letters， 2016， 117（3）：034301.

[19]L. P. Ye， C. Y. Qiu， J. Y. Lu， K. Tang， H. Jia， M. Z. Ke， S. S. Peng， Z. Y. Liu. Making sound vortices by metasurfaces[J]. AIP Advances， 2016，6：085007.

[20]C. J. Naify， C. A. Rohde， T. P. Martin， M. Nicholas， M. D. Guild， G. J. Orris. Generation of topological diverse acoustic vortex beams using a compact metamaterial aperture[J]. Applied Physics Letters， 2016，108：223503.

[21]X. Jiang， J. J. Zhao， S. L. Liu， B. Liang， X. Y. Zou， J. Yang. Broadband and stable acoustic vortex emitter with multi-arm coiling slits[J]. Applied Physics Letters， 2016，108：203501

[22]鄒丽，王乐，张士兵，赵生妹.基于波前校正的轨道角动量复用通信系统抗干扰研究[J].通信学报， 2015，36（10）：76-84.

[23]J. Wang， J. Y. Yang， I. M. Fazal， et al. Terabit free-space data transmission employing orbital angular momentum multiplexing[J]. Nature Photonics， 2012，6（7）： 488-496.

[24]B. Thide， H. Then， J. Sjoholm， et al. Utilization of photon orbital angular momentum in the low-frequency radio domain[J]. Physical Review Letters， 2007，99 （8）：87-91.

[25]F. Tamburini， E. Mari， A. Sponselli， B. Thide， A. Bianchini， F. Romanato. Encoding many channels on the same frequency through radio vorticity： First experimental test[J]. New Journal of Physics， 2012，14：033001.

[26]張维特.基于射频电磁涡旋的新型复用通信技术研究[D].浙江大学， 2017.

[27]张晗，杨军，毕宏振，王目光.一种基于轨道角动量复用技术的水声通信方法及系统[P].国家发明专利.CN， 201810424724.7.

[28]温生辉，蔡启富，汤军健，蔡嵩.厦门海域浅水三维潮流场动力学模型[J].海洋学报， 2003，23（2）： 1-17.

[29]杨定康，王彪.水声FBMC通信的双向判决反馈均衡研究[J].舰船科学技术， 2019，41（21）： 152-154.

[30]Q. Y. Li， C. B. He， Q. F. Zhang， K. J. Cheng. Passive time reversal based hybrid time-frequency domain equalizer for underwater acoustic communication[C]. IEEE International Conference on Signal Processing， Communications and Computing， 2016：1-6.

[31]刘梦，刘威，周志刚.基于线性因子更新的频域迭代判决反馈均衡[J].信号处理， 2019，35（10）：1739-1746.

[32]J. Huang， S. Zhou， Z. Wang. Performance results of two iterative receivers for distributed MIMO OFDM with large Doppler deviations[J]. IEEE Journal Oceanic Engineering， 2013，38（2）： 347-357.

[33]M. Beheshti， M. J. Omidi， A. M. Doost-Hoseini. Frequency-domain equalization for MIMO- OFDM over doubly selective channels[C]. 5th International Symposium on Telecommunications， 2010：1-6.

[34]X. Ma， C. Zhao， G. Qiao. The underwater acoustic MIMO OFDM system channel equalizer basing on independent component analysis[C]. WRI International Conference on Communications and Mobile Computing， 2009：568-572.

[35]M. Beheshti， M. J. Omidi， A. M. Doost-Hoseini. Time-domain block and per-tone equalization for MIMO-OFDM in shallow underwater acoustic communication[J]. Wireless Personal Communications， 2012，71（2）：1193-1215.

[36]J. X. Hao， Y. R. Zheng， J. T. Wang， J. Song. Dual PN padding TDS-OFDM for underwater acoustic communication[C]. 2012 Oceans， 2012：1-5.

[37]Y. Zhang， Y. V. Zakharov， J. Li. Soft-decision- driven sparse channel estimation and Turbo equalization for MIMO underwater acoustic communications[J]. IEEE Access， 2018，6：4955- 4973.

[38]Y. X. Ren， G. D. Xie， H. Huang， et al. Adaptive optics compensation of multiple orbital angular momentum beams propagating through emulated atmospheric turbulence[J]. Optics Letters， 2014，39 （10）：2845-2852.

[39]Y. X. Ren， G. D. Xie， H. Huang， et al. Adaptive-optics-based simultaneous pre- and post-turbulence compensation of multiple orbital-angular-momentum beams in a bidirectional free-space optical link[J]. Optica， 2014， 1（6）：376-384.

[40]Y. X. Ren， G. D. Xie， H. Huang， et al. Turbulence compensation of an orbital angular momentum and polarization-multiplexed link using a data-carrying beacon on a separate wavelength[J]. Optics Letters， 2015，40（10）：2249-2300.

[41]G. D. Xie，Y. X. Ren， H. Huang， et al. Phase correction for a distorted orbital angular momentum beam using a Zernike polynomials- based stochastic-parallel gradient descent algorithm. Optics letters[J]， 2015，40（7）： 1197-1200.

[42]R. W. Gerchberg. A practical algorithm for the determination of phase from image and diffraction plane pictures[J]. Optik， 1972，35： 237-250.

[43]M. I. Dedo， Z. Wang， K. Guo， Z. Y. Guo. OAM mode recognition based on joint scheme of combining the Gerchberg-Saxton （GS） algorithm and convolutional neural network[J]. Optics Communications， 2020，456：124696.

[44]J. Hill， M. D. Piggott， D. A. Ham， E. E. Popova， M. A. Srokosz. On the performance of a generic length scale turbulence model within an adaptive finite element ocean model[J]. Ocean Modelling. 2012，56：1-15.

[45]Y. J. Smith， H. S. Takhar. The calculations of oscillatory flow in open channels using mean turbulence energy models[D]. University of Manchester， 1977.

[46]U. Svensson. Mathematical model of the seasonal thermocline[D]. University of Lund， 1978.

[47]H. Burchard， H. Baumert. On the performance of a mixed-layer model based on the k-ε turbulence closure[M]. John Wiley & Sons.， Ltd， 1995.

[48]H. Burchard， O. Pertersen. Models of turbulence in the marine environment-A comparative study of two-equation turbulence models[J]. Journal of Marine Systems， 1999， 21（1）：29-53.

[49]K. L. Harper， S. V. Nazarenko， S. B. Medvedev， C. Connaughton. Wave turbulence in the two-layer ocean model[J]. Journal of Fluid Mechanics， 2014：309-327.

[50]楊天星，赵生妹.海洋湍流随机相位屏模型[J].光学学报， 2017，37（12）：1201001.

1. 南京信息工程大学滨江学院，江苏，214105

2. 海南大学信息与通信工程学院，海南 570228