汽车制动低频尖叫影响因素分析及NVH优化

张璐　王灿

摘要：针对车用盘式制动器常见制动噪音产生机理、影响因素及其常规解决措施进行介绍，并以低频制动尖叫特征为例，结合CAE及台架复现等噪音测量技术探究了噪音故障特征，通过建立复模态有限元模型并基于噪音机理对各零部件进行了噪音敏感度分析并提出相应NVH优化方案，最后针对噪音验证程序对优化方案进行了试验验证，这种台架软夹与硬夹相结合试验方式证明了CAE分析改进方法的有效性。

关键词：盘制动器;制动噪声;有限元;NVH优化;台架试验

0  引言

作為汽车客户高感知系统，制动噪音是汽车行业比较关注的行驶品质问题，同时制动NVH开发也是行业内的重难点课题[1]。由于制动系统本身是一个时变、非线性的系统，又具有单一性激励和系统性的激励的特征，同时又受大量外部不确定因素的影响，前期研究结果表明，制动摩擦材料、制动器结构、相关周边件的设计及不确定的外部环境都是影响制动噪音的关键因素[2]，正因为制动噪音的产生十分复杂，从制动系统稳健性设计优化的角度出发，寻找一套切实有效的制动噪音控制措施具有一定必要性。

以某车型低频制动尖叫（LF Squeal）特征为研究对象，基于CAE及噪音台架试验进行故障再现并完成该特征噪音机理分析，研究制动及周边零部件特征对该噪音敏感性并梳理出设计优化方案，对抑制制动低频尖叫的盘式制动器NVH开发具有一定的指导意义。

1  噪声机理

1.1 典型噪声特征

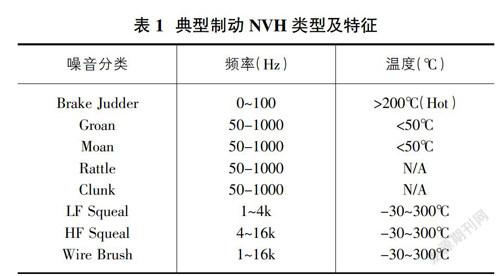
一般来说，常规制动噪音的主频比较单一，目前根据噪音频率分为低频噪音（<1000Hz）和高频噪音（>1000Hz），低频噪音主要涉及制动抖动、Groan及Moan，而高频噪音又分为低频尖叫（LF Squeal）和高频尖叫（HF Squeal），如表1，将这些典型制动NVH进行分类。

1.2 影响因素分析

制动噪音是通过摩擦副激励作用，两个或两个以上零部件共振，并通过制动角，悬架及车身传递到驾驶员耳部，因此从噪音激励源与传递路径角度，理论存在降低或者预防噪音的发生的可能。较为常见的是由制动系统自激励导致的制动尖叫，低频制动尖叫通常由卡钳支架与转向节的振动引起，同时制动盘与摩擦片，摩擦片与卡钳支架之间的压力分布也会影响到低频制动尖叫。因此从制动NVH开发层面可将制动噪音影响因素分为可控与不可控因素。

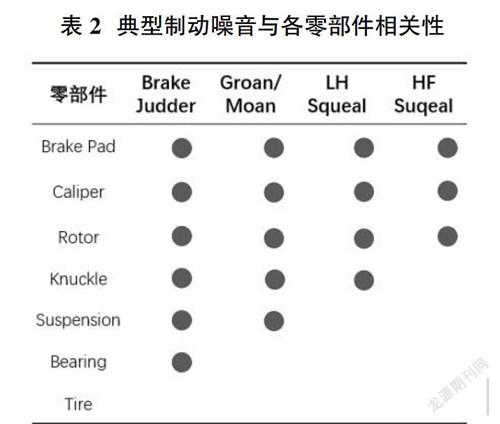
通过调整制动各零部件材质、结构刚度及相互配合方式等，进行抱怨噪音的抑制和预防，将此类因素作为噪音可控因素，如表2所示。可通过对特征噪音的分析确定摩擦材质、摩擦片设计、卡钳、制动盘及转向节结构变化对噪音敏感性，同时结合方案实施其他影响因素（如零部件配合与其他性能等）确定NVH优化方案。而不可控因素则主要涉及到以下几个方面：① 制动零部件磨损与老化，摩擦片与制动盘磨损所引起的压力分布与模态特征的变化，或消音片老化益胶失效等;②外部自然气候与气候的影响，涉及到环境温度、湿度、大气盐度等腐蚀相关的因素等，环境变化的交互可能会导致总成性能特征的变化，如高湿状态的摩擦系数会提升;③不良使用导致制动零部件物理特征的变化，如长期高温高压超过零部件设计范围会导致摩擦片表面形成釉面层，摩擦系数不稳定，同时其中起着隔振作用的树脂逐渐消耗，也不利于制动噪音的抑制。

2  特征低频尖叫问题

2.1 噪音描述

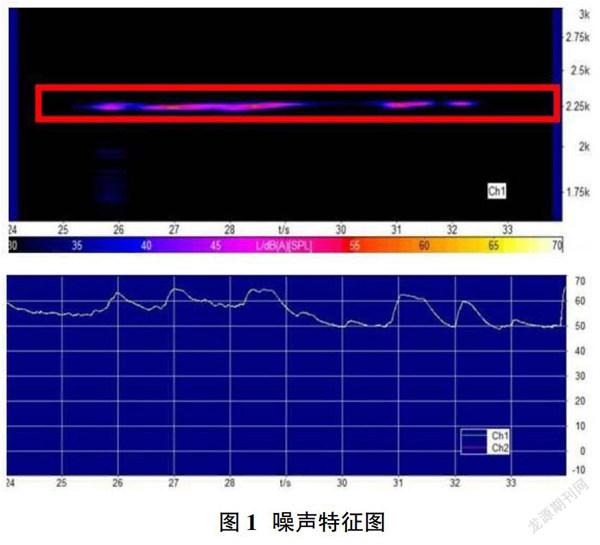
以某车型低频尖叫为例，当车速处于50km/h，初始制动盘温度处于150℃以上时，轻中制动时前制动角会产生制动尖叫，针对该现象进行故障再现，通过噪音工具进行特征分析，如图1所示，该制动噪音频率较为单一集中，为2.3kHz，处于低频制动尖叫，且最大声压达到了65dB。因此将进一步进行噪音台架复现，并针对卡钳、制动盘以及转向节等零部件进行模态分析，进一步锁定噪音耦合的主要贡献点。

2.2 模态分析

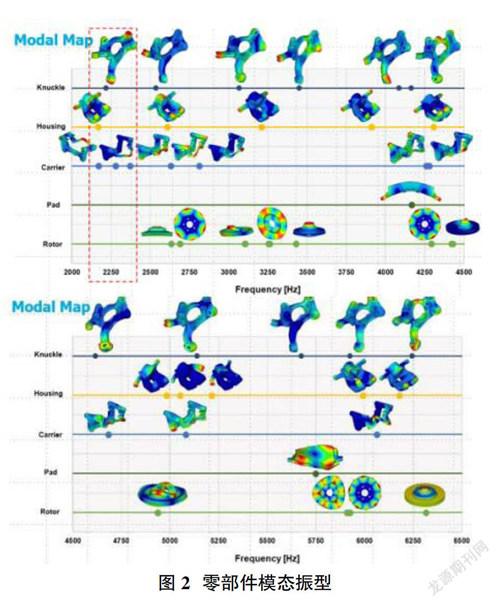
通过实模态分析对当前制动系统的动态特征进行研究，锁定噪音影响因子，为NVH优化方向提供依据。根据各部件频率分布范围进行1～8阶次模态分析，如图2所示为制动及相关零部件的结构模态振型，根据此动力学特征显示，与抱怨特征频率2.3kHz相关的零部件有转向节与卡钳支架，在转向节一阶模态及卡钳支架二阶固有频率与抱怨噪音存在耦合，而固有频率往往由其刚度、质量与阻尼决定，因此从结构设计方面可根据此特征确定后续对抑制2.3kHz低频尖叫的方向，同时根据对噪音机理分析结果，也可通过调整盘片间压力分布来改善该噪音，也作为后续对该噪音NVH优化方向。

2.3 噪音台架试验

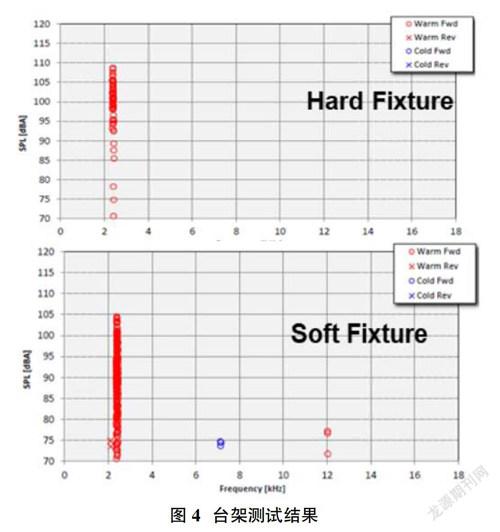
制动噪音台架测量技术能够排除天气、路面及人为因素影响，同时进行相应制动工况与测试条件的设置，一般来说惯量试验台在台架布置与工况设置方面较为灵活，且试验结果具有较好的一致性，因此其应用较为广泛。其中制动器夹具和周边件的设置则试验结果影响较大，如图3所示分别搭建硬夹与软夹周边环境，具有以下特点，硬夹具除连接制动器外，对轴承与转向节进行了刚性链接，更倾向于高频噪音捕捉;软件具模拟整车前悬，通过转向节连接了制动角、前悬架与转向拉杆，相对硬夹更易于探测频率较低的制动尖叫。

在台架上进行测试结果表面，两种夹具周边件类型均能稳定抓取到热态2.3kHz低频Squeal噪音，制动器温度均高于100℃，从复现频度上来看该噪音的可重复性较高，同时软夹试验对2.3kHz的复现稳定性更强，从这也验证也上一节所所阐述的该类型噪音产生机理。

3  NVH优化敏感性分析

3.1 有限元复特征计算

汽车制动系统运动方程可表示为[3][4]：

式中，m为系统平衡方程中的质量矩阵，c与k分别为阻尼矩阵和刚度矩阵，且、及分别表示系统在平衡位置附近的扰动加速度、速度及位移，？驻F为扰动外力。

式（1）系统平衡方程对应特征方程的通解则为：

式中，t为时间，而？滓i为第i阶模态的阻尼系数，？棕i为第i阶模态的模态频率，即分别表示阻尼系数及固有频率。同时阻尼比的定义为如下：

若阻尼比结果为正数，即该系统为典型的衰减振动系统，则为一个稳定的振动系统;反之，若该阻尼比结果为负数，系统则为一个发散的振动系统，系统表现为不稳定，因此根据系统阻尼比来预测该制动低频尖叫的发生趋势。根据上一节所研究的结果，建立制动卡钳、摩擦片、制动盘、转向节、减震器及转向横拉杆的三维模型并进行网格划分，如图5所示，建立包含制动角与前悬系统的有限元模型。

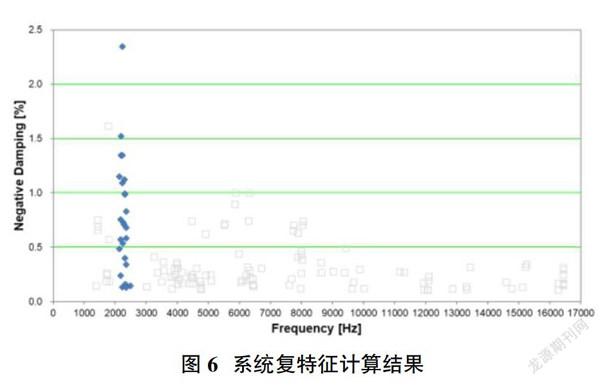
利用有限元复特征值分析方法计算原始制动角及周边配置下动态约束参数，如图6所示为系统不稳定频率与负阻尼比的关系，据经验当阻尼比小于0.01时的不稳定模态不易触发，可以看作是一个稳定的模态[5]，系统在频率为2.3kHz附近时的负阻尼比较大，最高达到了2.37，此时为一个不稳定模态，系统在工况下零部件出现了模态耦合，产生噪声的概率增加。

3.2 NVH优化方案

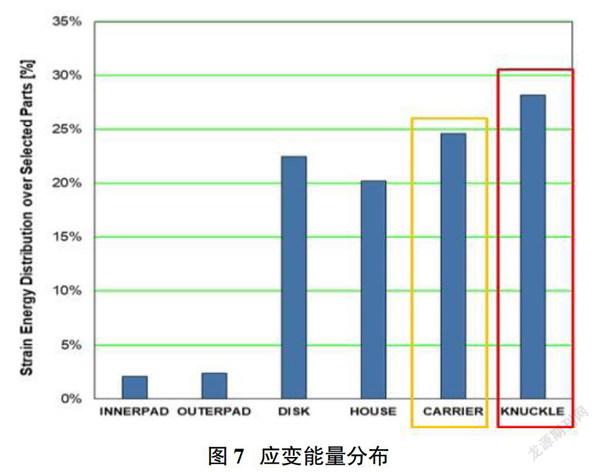
根据2.2节分析结果，该低频尖叫优化方向为转向节与卡钳结构的调整，以及摩擦片包角调整以改善制动盘与摩擦片的压力分布。如图7所示为系统主要零部件的应变能量分布，可以得出转向节为该热态2.3kHz噪音的最主要贡献零部件，达到27.6%，其次为卡钳支架占比24.7%。结合以上研究结果，将优化方向确定为：①转向节结构优化;②卡钳结构优化;③摩擦片包角设计调整。

3.2.1 转向节结构设计

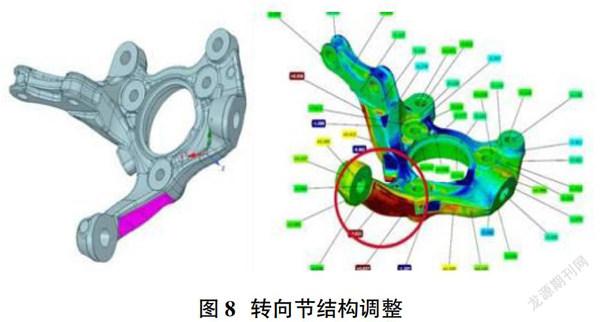
如上文模态分析结果显示，转向节在转向拉臂处刚度存在提升空间，因此如图8所示，将转向节转向拉臂处分别增加1mm与3mm，标记为方案1与方案2，调整后的转向节质量分别增加12g与30g。

3.2.2 卡钳支架结构设计

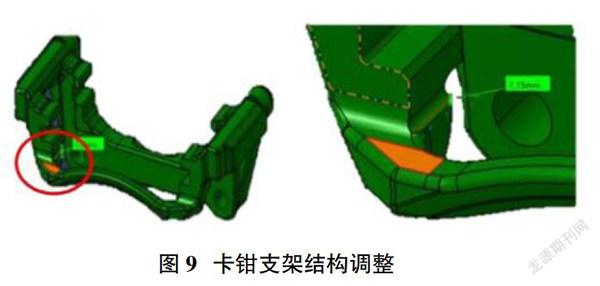
在2.3kHz不稳定频率附近，通过模态分析卡钳支架横梁的振幅较大，因此将支架横梁进行加固以提升刚度，如图9所示，横梁横截面处增加0.5mm，此时卡钳质量相应增加3.5g，将此方案标记为方案3。

3.2.3 摩擦片包角设计

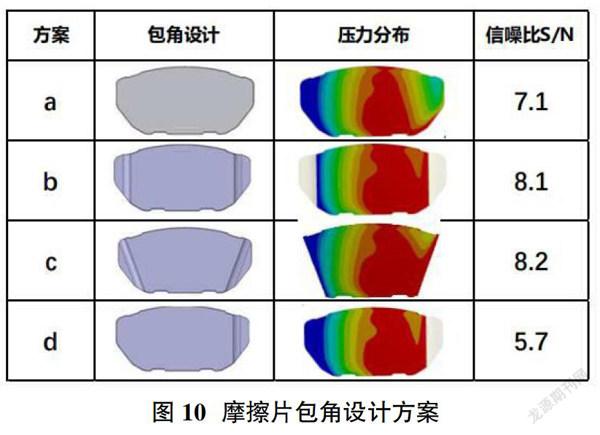
如图10所示，摩擦片包角设计方案包括a-d四种，a为baseline基础状态，b与c分别为平行倒角与扇形倒角方案，d为单侧平行倒角方案，信噪比是衡量信号质量优劣的指标，即为S/N在特定频段内信号功率与噪声功率的比值，因此S/N值越大表示噪音抑制倾向性越好，因此方案c作为摩擦片包角设计的主推方案，作为后续仿真及试验验证输入。

3.3 方案敏感性分析

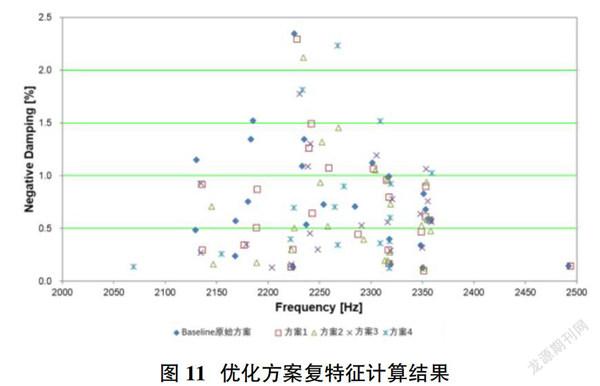
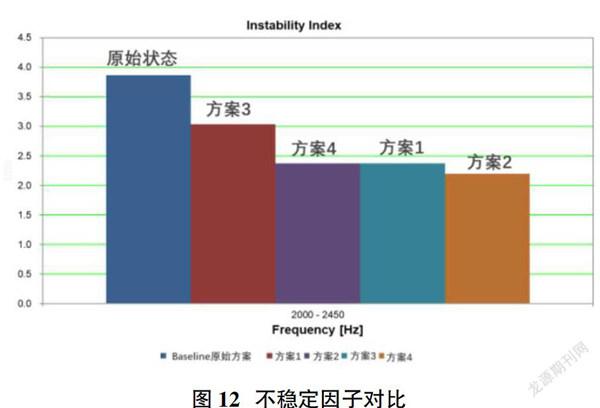
将方案1-方案4分别进行模型建立与设置，进行复特征值计算，并于原始状态进行对比，如图11所示为各方案的復特征值计算结果与原始状态的对比，可以得出，方案1-方案4的平均阻尼比均较原始状态相比，均有一定程度降低，具体来说将不同方案系统的阻尼比值进行加权，通过不稳定系数进行各方案的NVH评价，如图12所示，相比于原始状态，方案2的不稳定因子下降了近41%，方案1与方案4表现相当，不稳定因子下降了37%，而方案3相对原始状态的不稳定性也均有一定的效果，其不稳定因子下降了近19%。

当然，这四种方案也需要考虑系统其他性能，如摩擦片包角设计变更也会影响卡钳拖滞、偏磨等其他性能，这里不做详细探究。

4  基于优化方案的台架试验

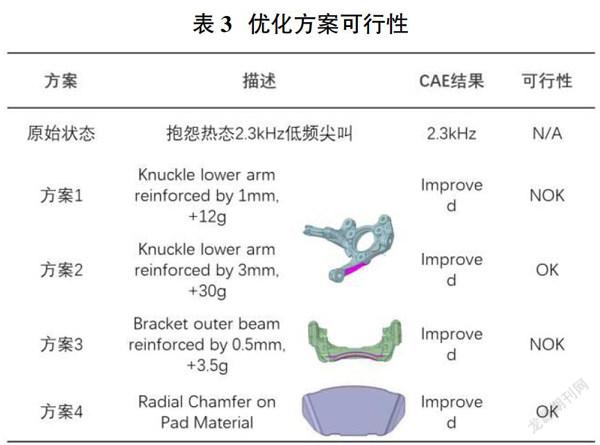
对方案1-方案4进行进一步台架试验验证，考虑到方案1与方案2均为转向节转向拉臂加固，且通过CAE计算结果方案1对2.3kHz噪音抑制性更强，因此将方案1作为第一个台架验证方案，另外，方案3对卡钳支架结构影响较大，且噪音稳定性表现相对一般，因此舍弃方案3，最后将方案4可操作性较强且噪音稳定性高，作为第二个台架验证方案。如表3所示为四种优化方案可行性研究结果，将选取方案2与方案4进行噪音软夹台架验证。

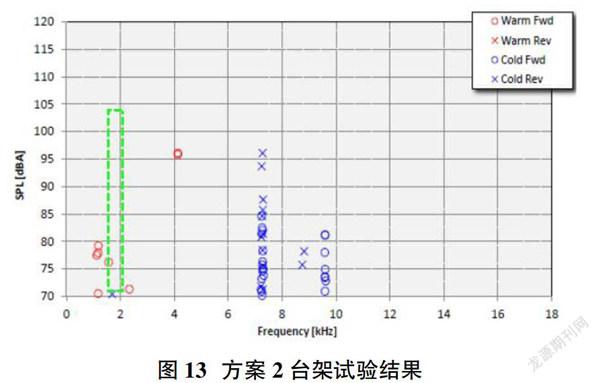
通过台架试验进行确认，并与原始状态进行确认，如图13所示为方案2转向节结构调整后的系统噪音试验结果，结果表面，2.3kHz热态低频尖叫仅出现1次，相对原始状态噪音出现概率降低了99%，但与此同时，其他制动工况与范围频率新增了一部分高频噪音，这是因为系统稳定性发生变化，从噪音发生的频次来说，相对原始工况方案2的整体噪音表现提升了66%，同时声压级也进一步降低。但对于最终NVH方案需要通过客户倾向度及抱怨工况复现难易程度进行平衡。

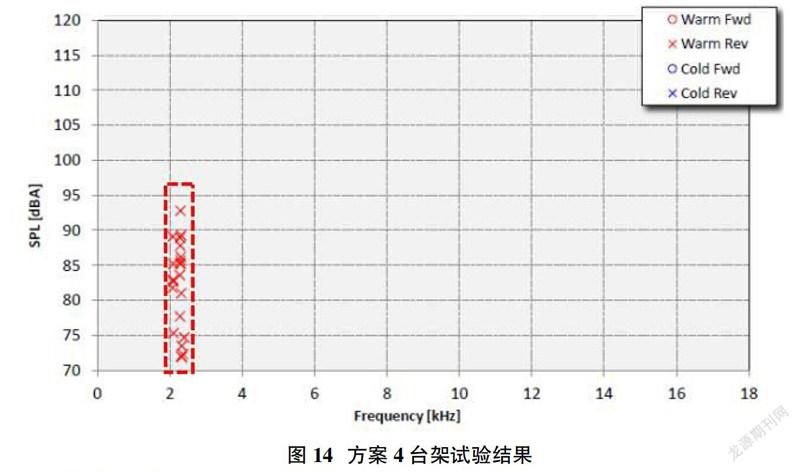
如图14所示为方案4摩擦片包角设计调整的系统噪音试验结果，结果显示，抱怨噪音2.3kHz得到了复现，但出现频次则大幅降低，相对于原始状态的噪音出现概率降低了80%，该工况的频段噪音得到有效抑制，但是相对方案2，其他频段系统更为稳定，但对于抱怨噪音2.3kHz的抑制程度则相对较弱。同时在平衡方案2与方案4的同时，也需引入制动系统其他性能评估因子，综合评估后选择更有利的方案。

5  结语

本文通过从噪音产生机理分析探究了制动系统噪音影响因素，并结针对典型噪音抱怨介绍了常规解决措施，以某车型低频制动尖叫为例，基于现有噪音测量技术CAE及台架试验进行故障复现及特征分析，并通过建立系统有限元模型进行了复特征仿真计算，得到系统各零部件的系统不稳定性因子，确定了抱怨噪音优化方向，该方法引入的系统不稳定性因子进行后续优化方向的把控，为制动系统特征噪音优化提供了思路。

基于噪音优化方案的倾向性研究及四种优化方案的复模态计算，最终锁定两种NVH方案并进行了台架试验验证，结果表面抱怨低频尖叫发生频次降低了80%以上，证明了该CAE优化方案的有效性。在提升整车舒适性的同时也提高了盘式制动器NVH开发效率。

参考文献：

[1]张立军，刁坤，孟德建，等.摩擦引起的振动和噪声的研究现状与展望[J].同济大学学报（自然科学版），2013（5）：765-772.

[2]CHEN F，TONG H，CHEN S E，et a1.On Automotive Disc Brake Squeal Part IV：Reduction and Prevention[C].SAE Paper 2003—0l-3345.

[3]陈家瑞.汽车构造[M].人民交通出版社，2006：305-307.

[4]LOUA G，WUA T W：BAI Z.Disk brake squeal prediction using the ABLE algorithm[J].Journal of Sound and Vibration，2004，272（3·5）：731-748.

[5]踏面制动尖叫噪声的有限元分析[J].机械工程学报.

[6]摩擦片偏磨引起的汽车制动低鸣噪声[J].机械工程学报.

[7]摩擦衬片包角对盘式制动器尖叫影响的仿真分析.

[8]廖鸿.盘式制动器制动噪音研究[D].

————————————

作者简介：张璐（1983-），男，上海人，中级工程师，硕士，主要研究方向为底盘制动系统设计与开发、汽车动力学。