数学非连续性文本的阅读策略教学研究
2020-09-10沈佳能
沈佳能
摘要:非连续性文本阅读能力的培养对学生数学的学习起到了重要作用。最近几年来,学生数学非连续性文本阅读能力的培养越来越受到教育者的关注,这也必将成为阅读问题的焦点。本文将以阅读表格形态文本和列表法为切入点,提出阅读表格形态文本的三步走策略和将复杂的信息通过列表法整理出来的两步走策略。
关键词:非连续性文本;表格形态;列表法;阅读策略
中图分类号:A 文献标识码:A 文章编号:(2020)-51-245
一、学生非连续性文本的阅读能力的现状研究
“非连续性文本”一词正逐渐进入教育者的视野,这一词源自国际“PISA”阅读素养测试项目,不同于“连续性文本”,“非连续性文本”是一种新型的阅读材料。但就现状而言,数学非连续性文本在理论层面上还存在以下问题。1、研究内容较为单薄、不够完整,比较碎片化和零散化。2、研究方法单一,没有深入的教学实践作为参考,没有提出完整的行之有效的教学方案。3、教师对学生缺乏有效的指导,导致了学生在阅读该非连续性类型文本时,在文本信息的理解、评价和运用等方面的能力有所欠缺。因此,对于基础的数学非连续性文本阅读,理应成为数学学科重点内容,关于此问题的思考和研究应当不断深入和继续。
二、小学数学教材中非连续性文本的特点研究
数学非连续性阅读与通常提到的阅读不同之处在于,数学教材中大量存在的是非连续性文本,而平时我们在生活中接触到的更多的是连续性文本的阅读。非连续性文本所表达的信息不是直接的,而是融合在数学条件和问题之中,以一些情境形态、导图形态、表格形态等非连续性文本存在,这就需要阅读者进行分析和整理。但“非连续性文本”有助于发展学生搜集信息、分析信息、处理信息的能力。所以,专家指出:学生阅读非连续性文本的能力更多源自学生的数学素养。数学非连续性阅读在思维的抽象性、严谨性和深刻性上更加凸显出数学学科的特点,因此数学学科也成为了培养学生非连续性文本阅读能力的一门重要学科。
三、数学非连续性文本阅读的教学策略研究
1、研究“非连续性文本”——以表格形态文本为切入点。
“表格形态”在数学教材中较为常见,作为非连续性文本的常见形态,表格的优点是让学生能直观地把握数学信息,其特点是比较性、条理性强。让学生学会阅读“表格形态”的文本是学生学好数学的一种有效途径。
1.1阅读表格形态文本的三步走策略
“表格形态”是数学教材中非连续性文本的常见形态,解答表格题的一般步骤大致可以分為三步。第一步识表,是考查学生获取信息的能力。识表是基础,是做好表格题的前提。第二步析表,即处理信息的能力。析表是关键,在识表的基础上,对表中的数据进行整理,理顺行、列的相关性,要进行纵向、横向比较,找出数据的变化规律。第三步说表,即表达信息的能力。将表格信息转变成文字信息,说表可谓是一个难点,是建立在识表、析表的基础上进行更深层次的理解性表达。
1.2阅读表格形态文本三步走策略示例
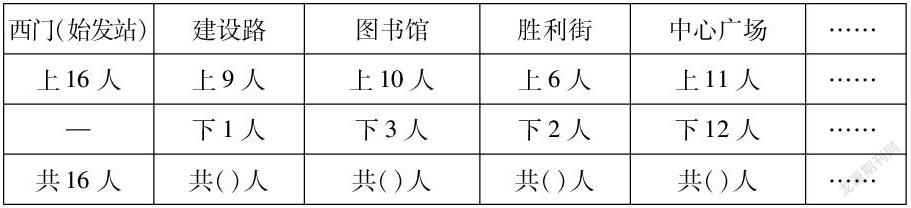
例1:下图是一辆公共汽车运行过程中上、下车人数的记录。从建设路开出时,车上的乘客有多少人?从图书馆、胜利街和中心广场开出时呢?算一算,填一填。
西门(始发站)建设路图书馆胜利街中心广场……上16人上9人上10人上6人上11人……—下1人下3人下2人下12人……共16人共()人共()人共()人共()人…… 步骤一:识表。阅读文字信息,结合表格发现这是一辆公共汽车运行途中的上下车人数的记录表。对表格的内容进行阅读,结合生活实际,了解表格信息,一辆公交车从西门出发(始发站),途经建设路、图书馆、胜利街、中心广场等。
步骤二:析表。分析文字信息,对表中的数据进行纵向、横向比较,找出数据的变化规律。从西门上车16人,到建设路上9人,下1人,到图书馆上10人,下3人,到胜利街上6人,下2人,到中心广场上11人,下12人等等。
步骤三:说表。将表格信息转变成文字信息。难点在于说一说汽车从西门站出发,这里为什么没有下车人数的记录?汽车行驶到建设路站时,上来了9人,下去了1人,括号里要填几人?行驶到图书馆时,上来了10人,下去了3人,括号里又要填几人?你是如何计算的?16+9-3=24(人),24+10-3=31(人)。还能有其他的方法吗?9-1=8(人),16+8=24人,10-3=7(人),24+7=31(人)。对于第二种解法的表达,需要学生能够纵向观察,说出建设路上来9人,下去1人,就是在建设路上来了8人,然后再联系西门上来的16人,进行加法计算。这种解法的表达对学生而言是学生的难点。只有理解到这一层次,才能对整张表格有一个全面的分析和认识。
2.研究“非连续性文本”——将复杂的信息通过列表法整理出来
学习将复杂的信息通过列表法整理出来的方式,能提高学生用列表法解决问题的能力。从而进一步深化学生对“表格形态”的非连续性文本的体验。在日常的数学学习中,数学信息都是融合在数学条件和问题之中,甚至有一些多余的信息,所以让学生学会对数学信息进行有意义的整理,可以有效的帮助和培养学生数学解决问题的能力,从而增强学习数学的兴趣和建立学好数学的信心。
2.1将复杂的信息通过列表法整理出来两步走策略
面对复杂的数学信息,学生首先想到的是把题目中的条件和问题摘抄下来,“列表法”对学生而言,有一定的挑战性。一是学生可能没有列表格的经验,数学教材的很多内容都是提供现成表格的。二是表格如何画、画几行、几列,如何填写,对于学生而言更加具有挑战。同时,要从复杂的数学信息中整理出有用的信息和数据,这也涉及到语文里的缩句知识,怎样把相关联的条件用简洁的文字表达出来对于学生而言,也同样具有很强的挑战性。
2.2将复杂的信息通过列表法整理出来两步走策略示例
例2:小芳家摘了3行桃树,8行杏树和4行梨树。桃树每行7棵,杏树每行6棵,梨树每行5棵,桃树和梨树一共有多少棵?
步骤一:认真审题,确定行与列。学生对条件进行筛选,有选择地整理出来,以下就是不同学生对题目信息整理的作品。
作品1:小芳家摘了3行桃树,每行7棵;摘了4行梨树,每行5棵。桃树和梨树一共有多少棵?
作品2:桃树3行,每行7棵;
梨树4行,每行5棵;
杏树8行,每行6棵。
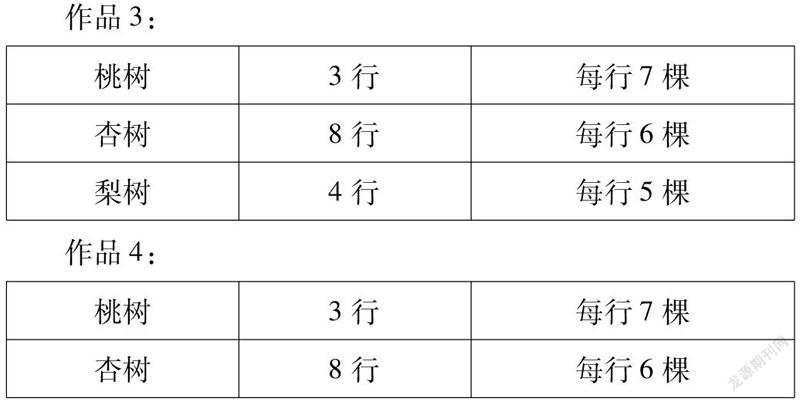
作品3:桃树3行每行7棵杏树8行每行6棵梨树4行每行5棵 作品4:
桃树3行每行7棵杏树8行每行6棵 步骤二:提炼关键信息和数据,力求表格简洁明了。从以上4项作品看来,这4位同学在摘取和整理条件时,有不同之处。有的用文字表示,有的用表格展示。有的从问题出发整理了两个条件,有的把所有的相关条件都整理了。面对学生不同的作品,首先,我们从作品1出发,对学生提出要求:能不能把文字改得更简洁些呢?从而建议学生把“小芳家栽了”、“桃树和梨树一共有多少棵”的字眼去掉。因为问题是不变的,我们要力求阐述的简单明了。这就实现了作品1到作品2的过渡。接着我们要探求文字与表格的相通之处,在文字上打上一些线,就可以实现文字和表格的转换。同时,说一说画表格整理条件有哪些好处?显然,画表格可以使题目的条件看起来更加清楚。这就实现了作品2到作品3的过渡。最后,比较作品3和作品4,作品3是从条件想起的,根据题中的条件,對3种树进行了整理。作品4是从问题想起的,根据题中的问题,只对2种树进行了整理。最终,我们确定作品4是最简洁明了的,也最符合列表法的二步走策略。
四、结语
综上所述,本文希望通过阅读“表格形态”的文本,让学生感受和体验这一非连续性文本类型,从而习得阅读表格形态文本的三步走策略。提高学生解读数学文本、分析数学文本的能力。接着,通过学习将复杂的信息以列表法整理出来的方式,提高学生用列表法解决问题的能力。从而进一步深化学生对以“表格形态”的非连续性文本的体验。
参考文献
[1]徐静.“综合同构”:非连续文本阅读教学策略[J].江苏教育,2017(43).
[2]孙文英.数学非连续性文本阅读心理过程初探[J].林区教育,2012(4).
[3]吴秀丽.重视数学非连续性文本阅读提升学生审题能力[J].福建教育学学报,2018(06):68-70.
