多级离心泵固液两相流动特性及压力波动分析
2020-09-10吴杰王延峰王玉川
吴杰 王延峰 王玉川








通讯作者:王玉川,1983年10月,男,汉族,河南林州人,现任职于西北农林科技大学水利与建筑工程学院,副教授,博士研究生。研究方向:水力机械内部流动及运行稳定性计算分析;射流冲蚀沙床塑造异重流的水动力学过程和机理研究。
基金项目:陕西省水利科技项目(基金编号:2018slkj-8);国家自然科学基金项目(基金编号:51809218)。
摘要:以煤矿用某型号多级耐磨离心泵为研究对象,利用SST湍流模型和Euler-Euler非均匀多相流模型对其内部不同流量工况的固液两相非定常流动进行了数值模拟和计算结果的时频分析。结果表明,随着流量的增加,叶轮内发生流动分离的位置和低固体颗粒体积分数区域由吸力面向压力面转移,正导叶流道内出现较大范围的漩涡结构,反导叶内的旋涡范围和湍流动能均逐渐增大;漩涡区域的固体颗粒受离心力作用出现滑移,中心区域固体体积分数较周围区域低。叶轮和正导叶的动静干涉作用下,各级叶轮流道内、叶轮出口压力面附近的压力波动主频主要为导叶叶频,正、反导叶流道内的压力波动主频为叶轮叶频。叶轮内流动的不稳定性导致叶轮流道出口中间位置和吸力面侧易出现叶轮叶频。
关键词:多级离心泵;固液两相流;非定常流动;压力波动
一、前言
多级离心泵的突出优点是高扬程,同时也存在流动更加复杂多变、不易于预测等弊端[1-3]。固相的掺入时常发生在泵的实际输送介质过程中,其改变了泵内原有的内部流动,容易引发振动、噪声、磨损等问题[4-8]。
常见的固液多相流数值计算模型主要包括Mixture和Particle两种,近几年Particle非均相流模型被越来越多的应用到流体机械的模拟中[9-13]。韩伟等[14]基于大涡模拟和Mixture多相流模型探究了颗粒的存在对离心泵内部压力脉动的影响,发现小流量工况时,颗粒增強了动静叶栅交界处的高频压力脉动,减弱了导叶内的高频压力脉动;大流量工况时,颗粒削弱了动静叶栅交界处的高频压力脉动,增强了导叶内的高频压力脉动;蜗壳内的压力脉动不受颗粒的影响。刘建瑞等[15]运用Simple算法和Mixture模型研究了流量对颗粒分布的影响,结果表明,流量的变化改变了颗粒进入叶轮流道的角度,较大流量工况时,颗粒的运动轨迹更加明显。廖娇等[16]采用Particle模型对离心泵全流道进行了数值模拟,发现流量较小时,固液两相流时的泵扬程大于清水工况,当流量超过40 m3/s时,清水下的扬程高于固液两相流工况,固体颗粒的掺入降低了离心泵的效率。曹卫东等[17]以某型两级离心泵为模型分析了其内部非定常压力分布特性,表明叶轮出口处的压力脉动主频率与叶轮叶片数、正导叶数均有关,叶片与导叶的动静干涉作用是影响压力和扭矩波动的主要因素。马新华等[18]在设计工况下对多级离心泵两级流场进行了非定常数值模拟,发现叶轮与导叶间的动静干涉是产生压力波动的原因,且正导叶内的压力脉动受到整体式冲压叶轮形状的影响,导叶内脉动主频表现为叶轮叶频压力脉动。
本文基于Particle非均匀多相流模型和SST湍流模型,数值模拟了煤矿用某型多级离心泵内的非定常固液两相流动,分析了不同流量工况下的内流特性和压力波动规律。
二、计算方法
(一)计算模型
研究采用的多级(3级)离心泵基本参数如下:设计流量Qopt=280 m3/h,单级扬程H=42.5 m,转速n=1480 r/min,比转速为89,叶轮叶片数Z1=7,正导叶叶片数Z2=8,反导叶叶片数Z3=8。首级叶轮进口直径为180 mm,次级和末级叶轮进口直径为156 mm,叶轮外径均为360 mm。
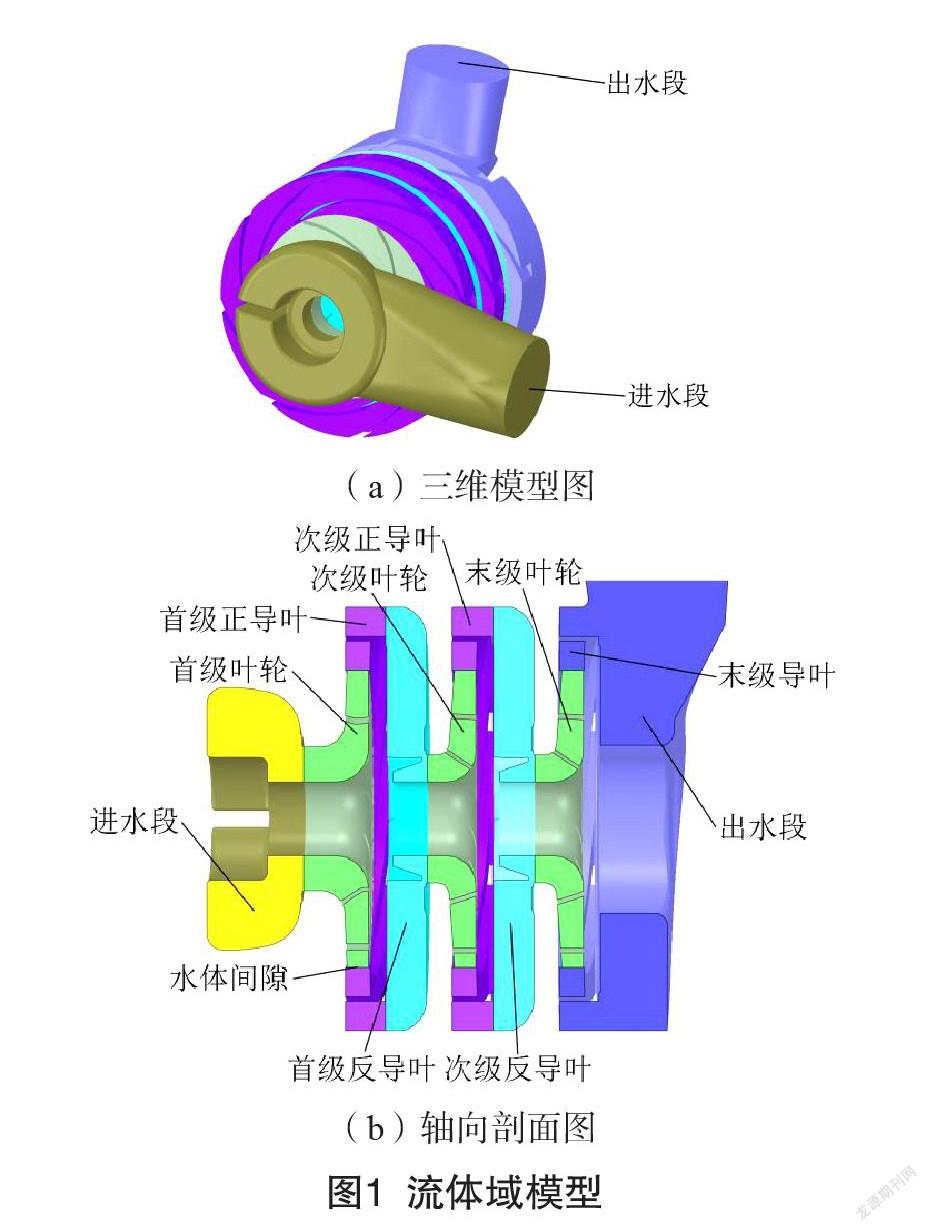
流体计算域主要包括进水段及其延长段、首级叶轮、首级导叶、次级叶轮、次级导叶、末级叶轮、末级导叶、出水段及其延长段,如图1所示(省略进出口延长段)。考虑到进口和出口可能产生回流,适当延长进水段和出水段(4倍管径)。
(二)网格划分
多级离心泵结构复杂,尺寸跨度较大,因此流体域采用适应性较好的四面体非结构化网格。划分5套不同疏密程度的网格,分析其网格无关性,如表1所示,可见随着网格数的逐渐增加,数值计算扬程H的最大变化范围为1%,基本保持稳定。综合考虑计算精度和时间,选取第一套网格作为计算网格。
(三)数值计算方法和边界条件
湍流模拟采用SST模型,此模型考虑了湍流剪切应力的传输,预测流动的开始和负压力梯度条件下流体的分离量具有较高的精度。固液两相流动选取欧拉-欧拉非均匀多相流模型,考虑了每一相独立的速度场和其他相关场的情况,压力场由两相共享,两相间通过相间转移项相互作用。相间传递设置为Particle Model子模型。
结构尺寸跨度较大,故数值计算选用双精度模式。液体设置为连续相,固体颗粒设置为离散相,为粒径0.1 mm的单一材质(沙子)均匀球体。假定进口处液体与固体颗粒均匀分布,液相体积分数为90%,固相体积分数为10%。边界条件设置为速度进口、静压出口,壁面是无滑移边界条件。首先对泵内流场开展单相和多相的定常计算。将定常计算的结果作为初始值,分别进行0.8Qopt、1.0Qopt、1.6Qopt流量工况的非定常固液两相流动计算。计算总时长设置为0.81081s,即叶轮转动20周,时间步长设置为0.00045 s,即每一个时间步长叶轮转动4°。
监测点的位置如图2所示。首级叶轮沿进口到出口方向设置监测点D1、D2,叶轮出口圆周方向沿压力面到吸力面设置监测点D3、D4、D5,首级正导叶内沿流动方向设置监测点D6、D7、D8,反导叶内设置监测点D9、D10。次级、末级流道监测点设置与首级类似。出水段设置监测点D29。
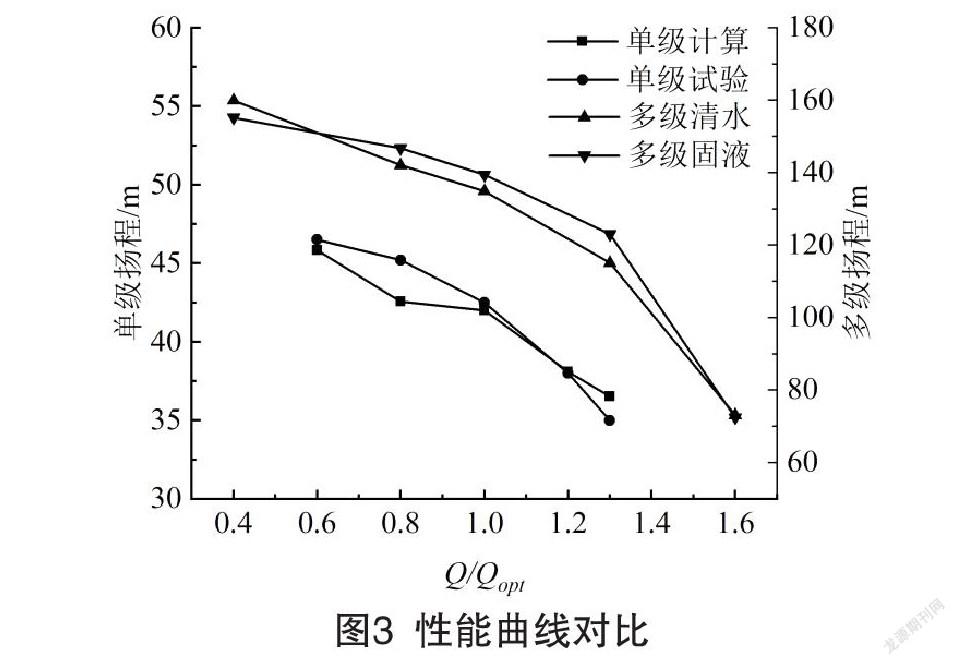
依据单级离心泵定常计算结果和多级离心泵非定常计算结果绘制扬程性能曲线,如图3所示。发现单级离心泵清水介质的数值计算性能曲线和实验变化趋势一致,两者的最大误差在5%左右,说明了数值计算模拟泵内主要流动特征的可靠性。多级离心泵输送清水和固液两相介质时的性能曲线在大流量工况和小流量工况相交,而在最优工况附近时,多级离心泵输送固液两相流体的扬程大于清水介质。
三、结果与分析
(一)流线分布规律
选取固液两相流非定常计算0.81 s的瞬态流场,分析泵内流线的分布情况。图4为次级叶轮和正导叶径向截面的流线分布。可以看到,随着流量的增加,流线变得平滑均匀,叶轮叶片发生流动分离的位置由吸力面逐渐转向压力面侧。叶轮内的流线受到叶轮和导叶叶片时序效应的影响,分布不均匀,从而导致径向力周向分布不均匀,这是离心泵的振动源之一。同时,流线在叶轮进入正导叶流道时发生了急剧转折,加剧了局部的能量损失。
随着流量的增加,流体更易从叶轮平稳流入正导叶流道。各正导叶流道凸壁面处容易产生旋涡、堵塞流道,湍流旋渦的强度随流量的增加而增大。不同流量工况正导叶流道内流动存在显著差异。
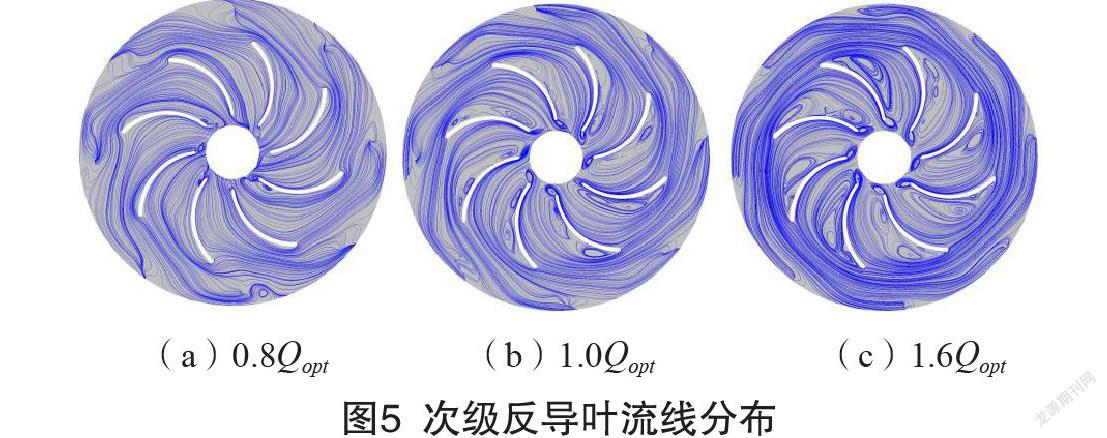
次级反导叶内流线分布如图5所示,水体从反导叶无叶区流入反导叶流道的冲击角度随流量的增加单调增大,导致流量越大,反导叶流道内的流动越紊乱。1.6Qopt工况时流线几乎平行于圆周方向,且更易导致相邻相位无叶区域的水体跨流道流入。反导叶叶片内的流动分离发生在叶片凸面侧,且旋涡范围随着流量的增加而增大。正、反导叶流道内的旋涡,会引起较大的能量损失。
(二)固相体积分数分布规律
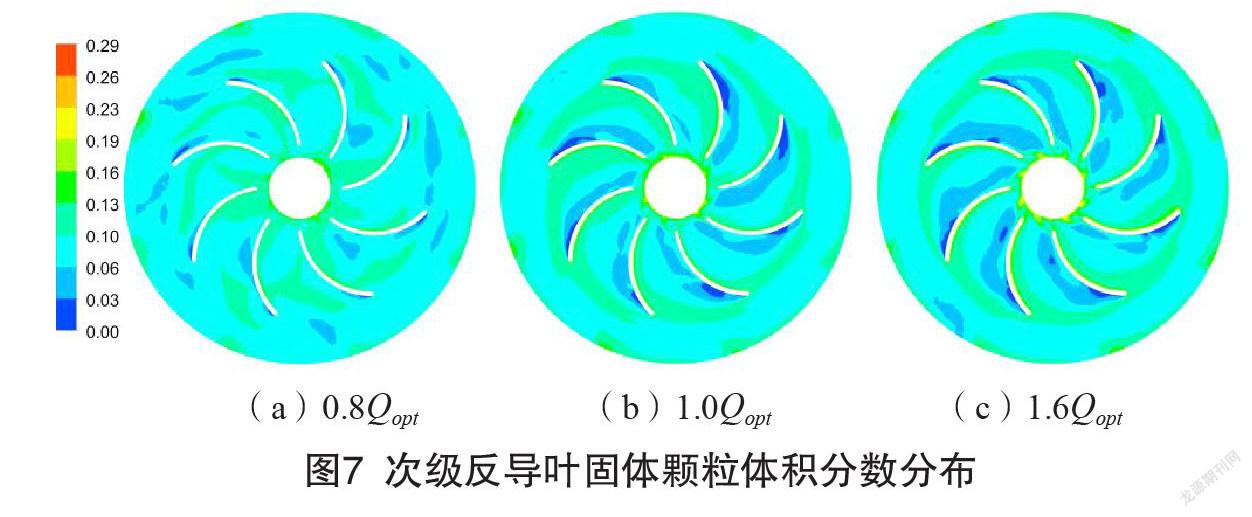
图6-7分别为次级叶轮和正反导叶内非定常计算0.81 s的固相颗粒体积分数分布情况。随着流量的增加,次级叶轮叶片吸力面侧的固体颗粒体积分数增大,低固体颗粒体积分数区域向压力面侧转移,这是冲击角发生变化后流动分离位置发生改变导致的。动静干涉作用下,正导叶流道内固体颗粒分布不均匀性增强。结合流线分布规律,发现旋涡处固体颗粒体积分数较小,原因是固体颗粒在离心力作用下向漩涡外侧滑移。
次级反导叶流道内低固体颗粒体积分数区域主要集中在反导叶凸面侧,这是流动分离形成旋涡的结果。
(三)湍流动能分布规律
图8为非定常计算0.81 s时刻多级叶轮叶片表面的湍流动能分布。总体看来,各级叶片表面吸力面的湍流动能大于压力面,且数值随着流量的增加而增大,叶片表面边界层流动的紊动增强,因此,产生更多的能量耗散。小流量工况时,叶轮出口压力面侧在动静干涉作用下容易产生局部较高湍流动能。
次级叶轮和正导叶内的湍流动能分布如图9所示。次级叶轮和正导叶内的湍流动能在设计流量工况时最小,大流量工况时,液体以更大的进口相对速度角和速度进入叶轮流道,使整个叶轮流道前端产生较高的湍流动能损失。正导叶流道相比叶轮产生了更大范围的旋涡,导致其内部湍流动能较大,偏离设计流量工况时,高湍流动能区域几乎充满整个正导叶流道,极大地消耗了能量水头。
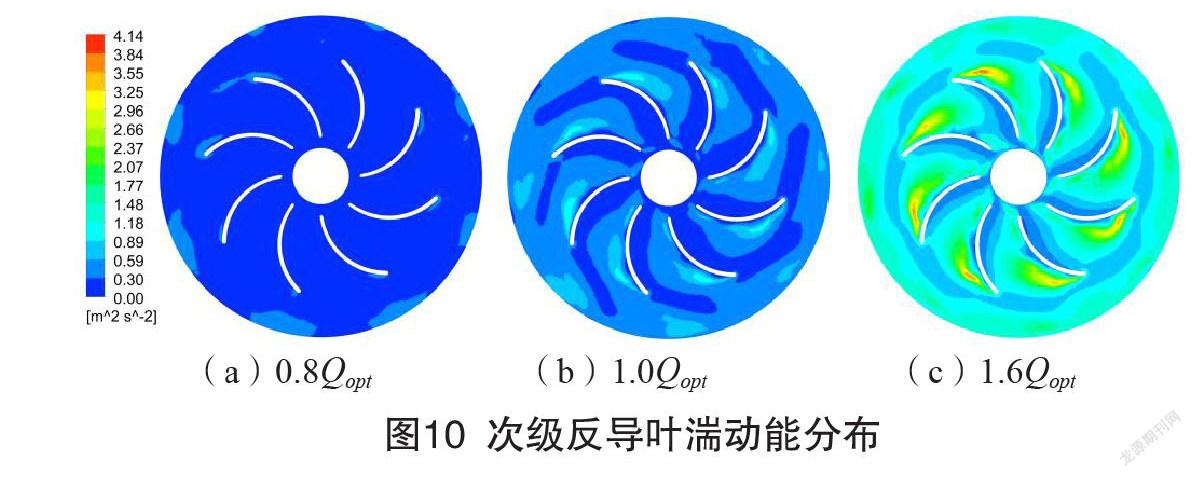
图10为次级反导叶流道内的湍流动能分布。可以看到随着流量的增加,湍流动能逐渐增大,这是因为相同的过流断面,流量的增大导致流速增大,从而雷诺数增大,紊动增强。各流量工况时,反导叶进口处凸面侧容易发生流动分离,是高湍流动能区域,且反导叶凸面侧的湍流动能总体大于凹面侧。
(四)压力波动规律分析
1. 压力波动的时域特征
分析稳定后最后一个旋转周期的压力波动情况。压力波动的分析采用无量纲压力系数Cp表示,计算公式如下:
式中Pi为监测点实时压强,Pa;ρ为水的密度,kg/m3;g为重力加速度,m/s2;Hi为多级离心泵输送固液两相流介质时各流量工况所对应的扬程值,m;u为叶轮出口圆周速度,m/s。
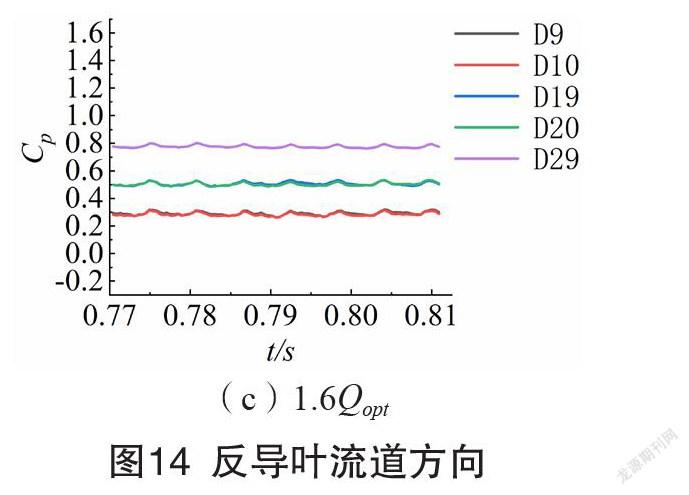
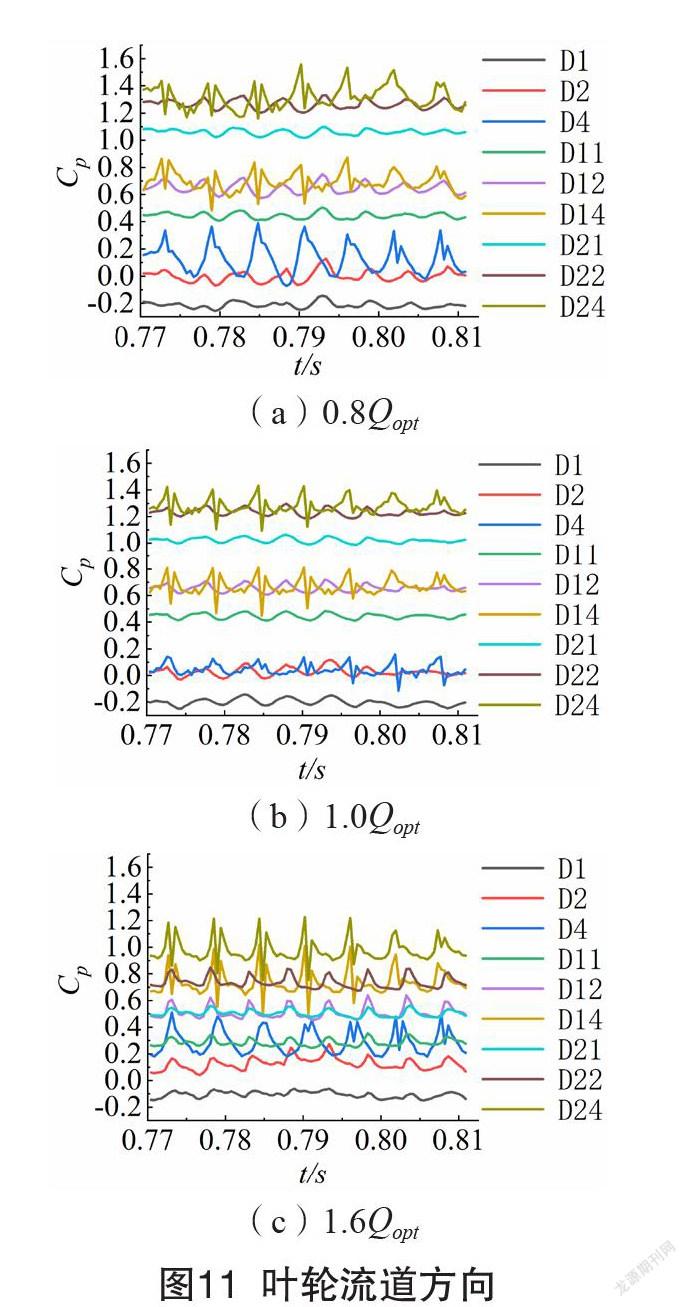
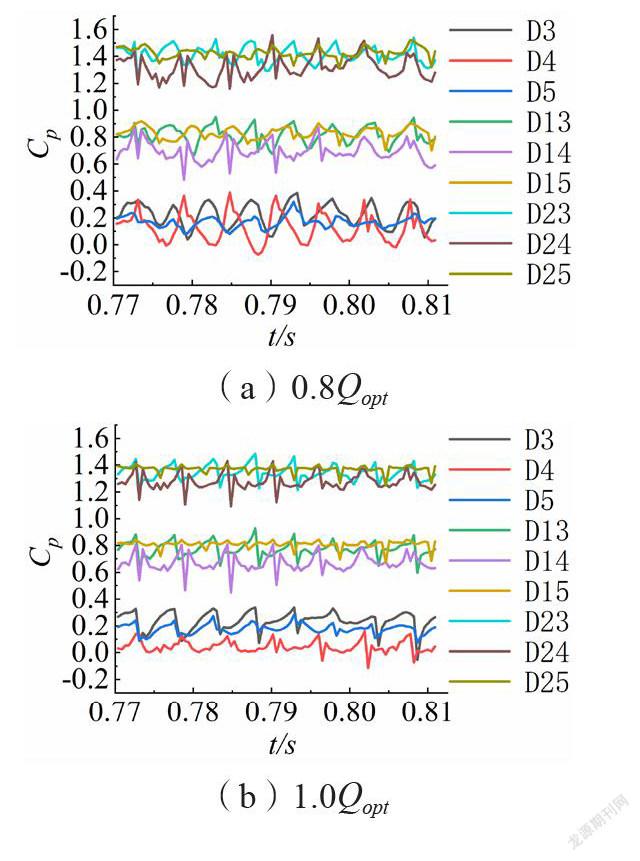
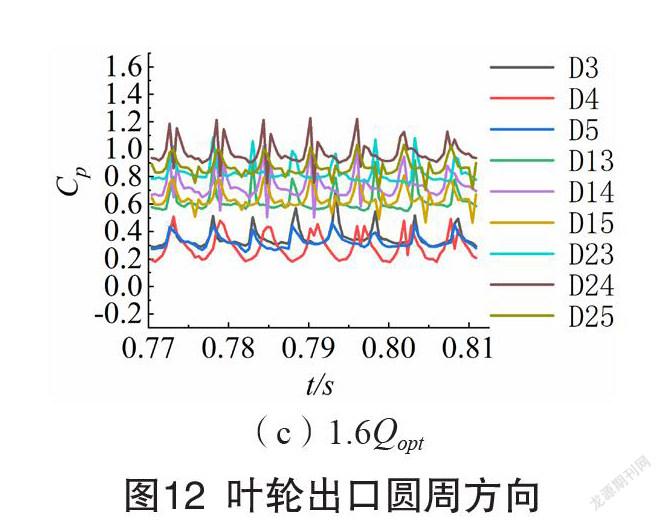
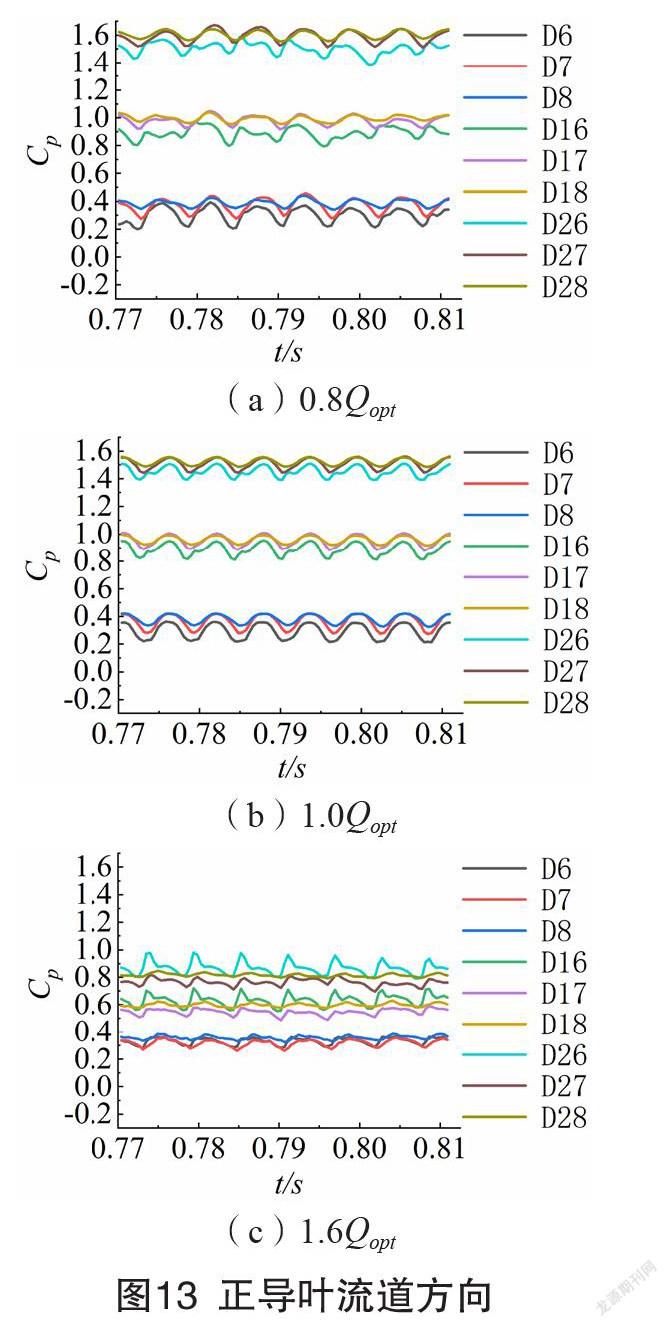
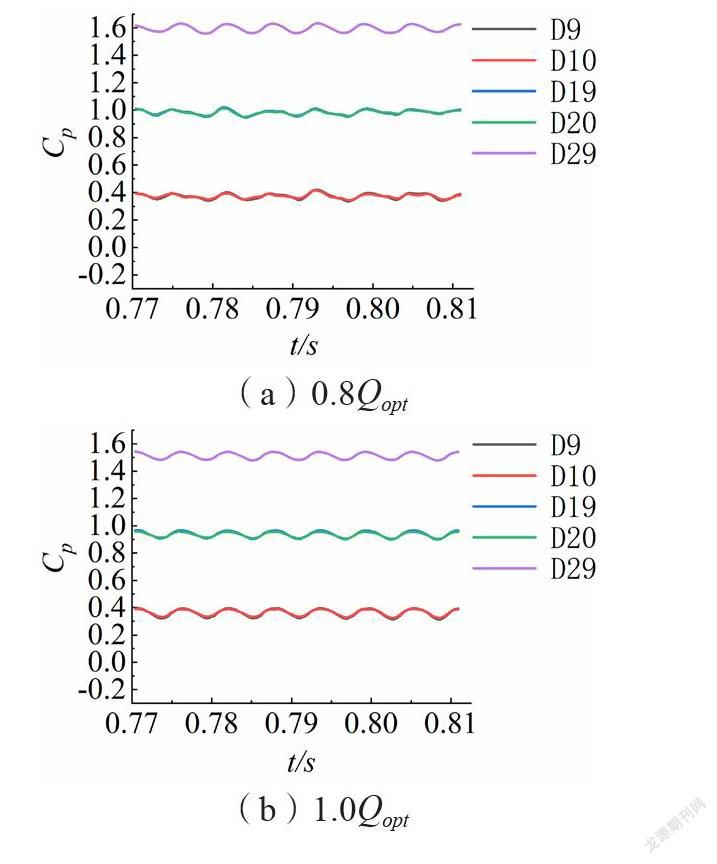
监测点压力波动时域图如图11-14所示。压力系数随着级数的增加而增大,并且沿叶轮进口到出口方向逐渐增大,符合泵的能量转化基本规律。因为叶轮出口液体具有较高的速度环量,且与正导叶发生动静干涉作用,导致其流动复杂、压力波动比多级离心泵内其他部位更加剧烈。各级反导叶内监测点压力波动最弱且各点的压力波动曲线近似重合。
叶轮旋转一圈时间,多级离心泵内各监测点压力波动周期性主要与叶轮或者导叶的叶片数相关。各级叶轮进口附近(D1、D11、D21),设计流量工况时一个旋转周期内出现了7个类似的波峰波谷;偏离设计工况时呈现出8个相似的波峰波谷。叶轮流道内(D2、D12、D22),各流量工况下均呈现出8个周期性波动。叶轮出口圆周方向位置压力面附近(D3、D13、D23)的压力波动,均表现为8个相似的波峰波谷;圆周方向中间位置(D4、D14、D24)和吸力面侧(D15、D25)呈现7个波峰波谷。正、反导叶流道中,压力波动时域曲线在一个叶轮旋转周期内均出现7个类似的波峰波谷。
0.8Qopt和1.0Qopt工况时,扬程相对较高,不同级数之间的压力系数差值较大,而1.6Qopt工况时,各级监测点的压力系数差值减小。
2. 压力波动的频域特征
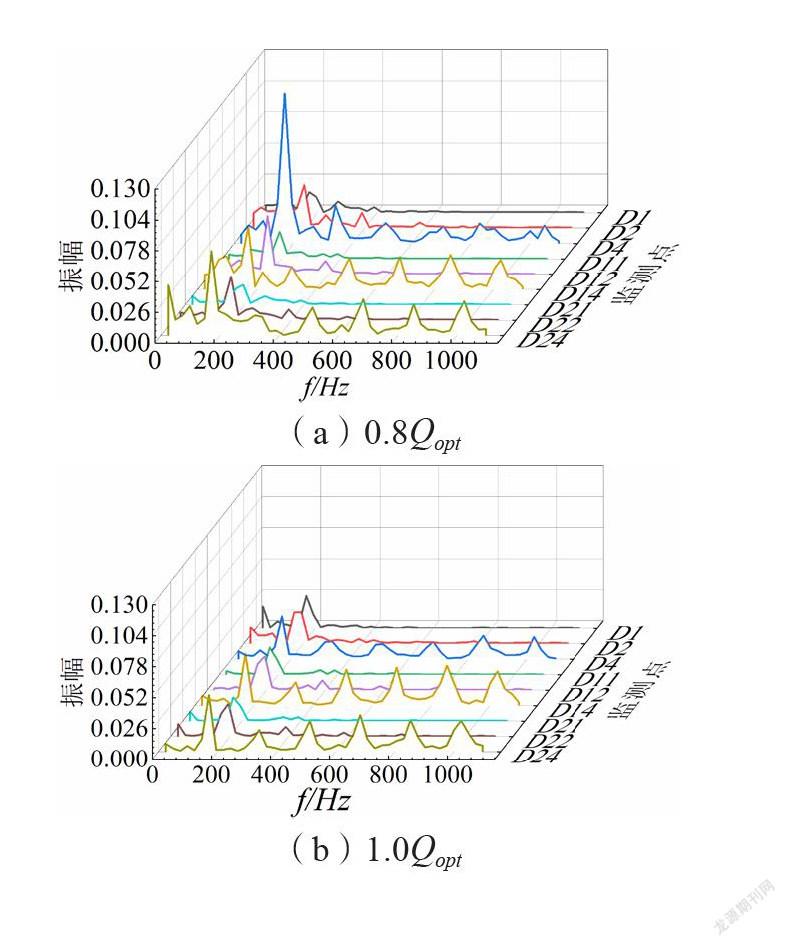
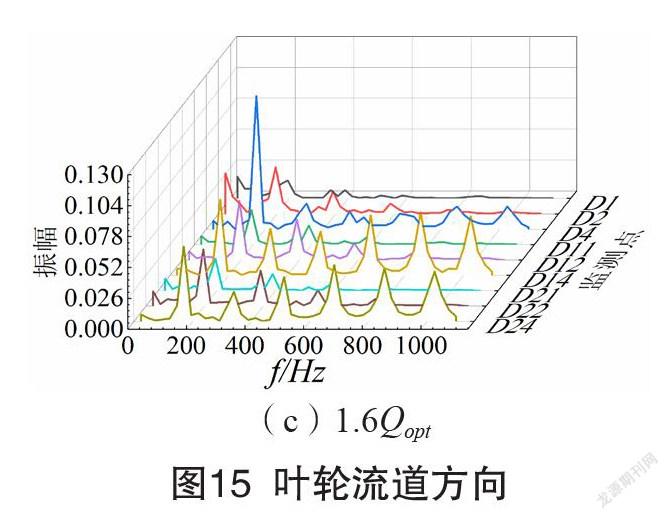
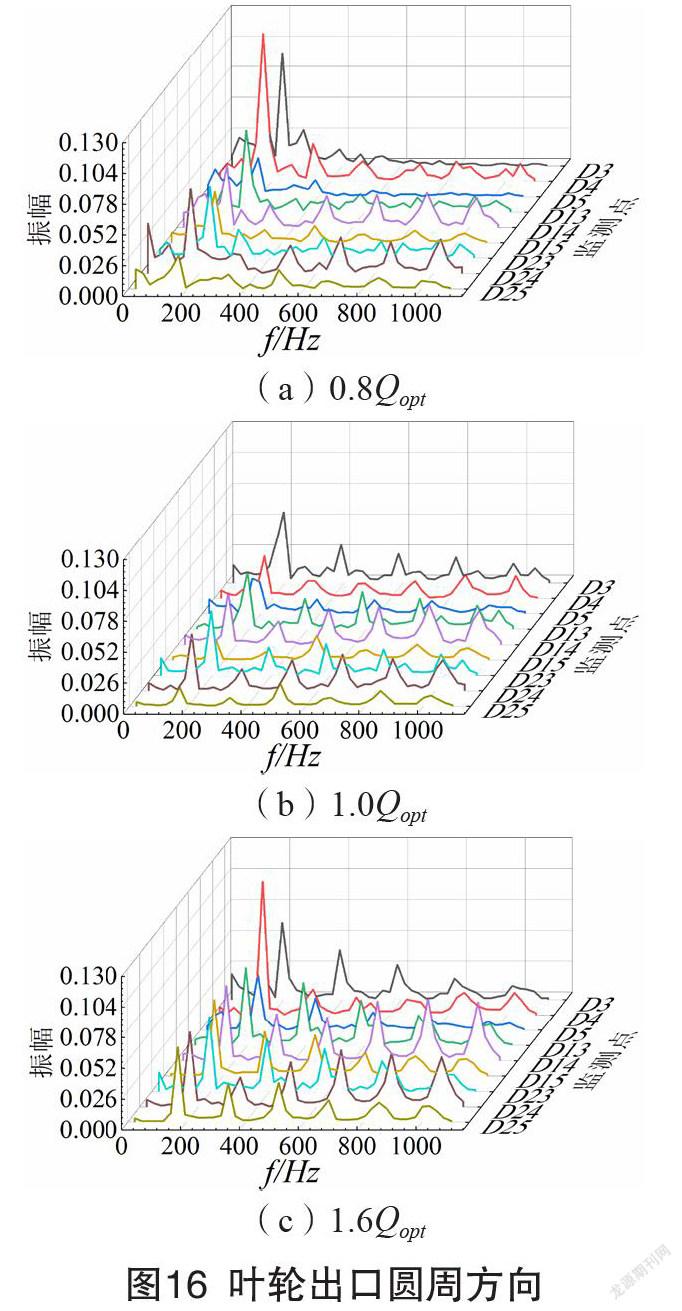
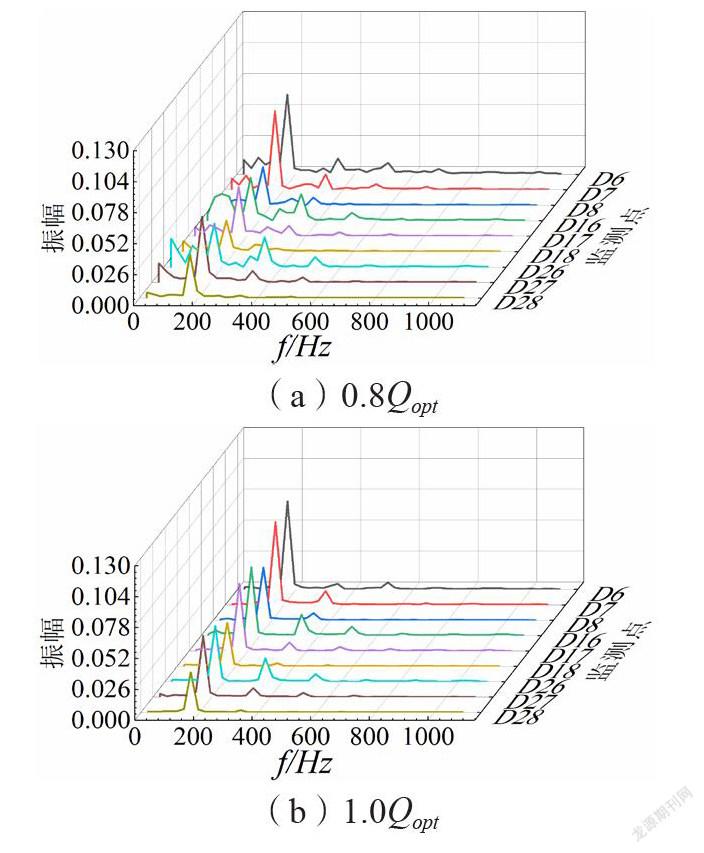
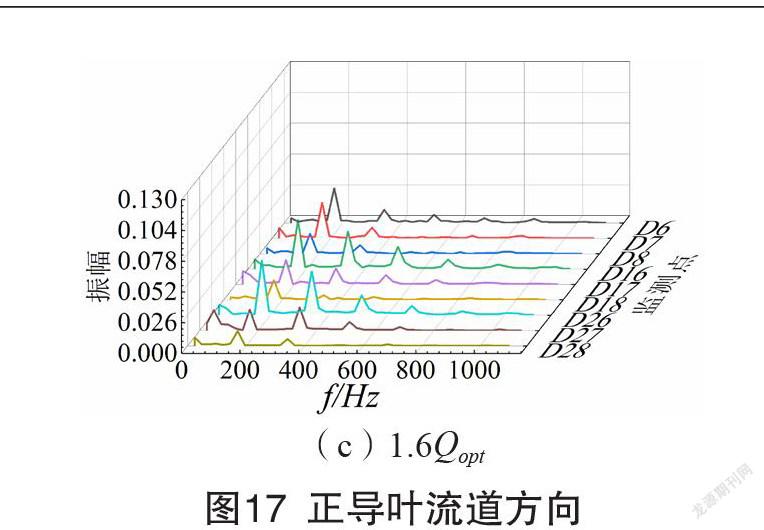
经过快速傅里叶变换,监测点各流量工况时的压力波动频域图如图15-18所示。此多级离心泵叶轮转速为1480 r/min,则转频为24.67 Hz,叶轮叶片数为7,求得叶轮叶频(单个正导叶叶片相对叶轮叶片运动的转动频率)为172.67 Hz,导叶叶片数为8,则导叶叶频(单个叶轮叶片通过正导叶叶片的频率)为197.33 Hz。总体上,时域图中波动周期性与叶轮叶片数相关的监测点主频为一倍叶轮叶频,波动周期性与导叶叶片数相关的监测点主频为一倍导叶叶频,且分频频率表现为相应叶轮或者导叶叶频的整数倍。
各级叶轮进口附近(D1、D11、D21),设计流量工况时为叶轮叶频,其中首级的压力波动由叶轮和进口段的动静干涉作用引起,次级和末级由反导叶流道的压力波动传播而来;偏离设计工况时为导叶叶频,受到叶轮和正导叶的动静干涉作用向上游传播的影响。叶轮流道内(D2、D12、D22)均为导叶叶频,表明其压力波动主要受到叶轮和正导叶的动静干涉作用向上游传播的影响。各级叶轮出口压力面附近(D3、D13、D23)的压力波动,主频均为导叶叶频,是叶轮和正导叶动静干涉作用的结果;叶轮出口中间位置(D4、D14、D24)和吸力面附近(D15、D25)受到叶轮内不稳定流动支配,主频为叶轮叶频;正、反导叶流道中,压力波动主频为叶轮叶频,是叶轮和正导叶的动静干涉波动向下游传播的结果。
大部分监测点主频和分频随流量工况的变化未发生改变,但是对应的振幅有所变化。设计流量工况,叶轮内监测点的压力波动幅值较非设计工况弱;正、反导叶内的压力波动幅值在大流量工况较设计工况弱;大流量工况下正、反导叶流道内虽然出现了较大范围的漩涡结构和较强的紊动,但是由于流体微团之间的约束作用较强,流动结构(漩涡结构)随时间变化的幅度较小,所以压力波动幅值较小。相同流量工况时,叶轮出口处监测点的压力波动最剧烈,压力波动振幅总体较大,且此区域频域区间分布最广,存在大量高频率的分频。不同级的监测点频域图存在差异,首级叶轮中出口处的监测点在非设计工况出现了主频振幅显著增大的现象,说明首级叶轮流道内的流动不稳定性最强。
叶轮内沿流动方向,由于受到的叶轮和正导叶动静干涉作用越来越大,导致压力波动愈发强烈。叶轮出口圆周方向中间位置的压力波动强度较压力面和吸力面更加剧烈。正导叶内沿流动方向,动静干涉作用引起的压力波动逐渐衰减,导致压力波动强度逐渐减弱。
四、结论
第一,叶轮与正导叶的时序效应引起周向流场的不对称分布。设计工况时,叶轮流道内流动稳定,压力波动较弱;小流量工况时,叶轮流道内发生吸力面脱流,低固体颗粒区域集中在吸力面,动静干涉作用强烈;大流量工况,发生压力面脱流,低固体颗粒区域集中在压力面,正导叶流道内逐渐形成较为稳定的大尺度涡结构,在漩涡区域,固体颗粒受离心力作用发生滑移,漩涡中心处的固相浓度低于周边区域。
第二,反导叶流道内,随着流量增大,导叶头部的流动分离现象趋于严重,漩渦范围增大,流动的紊动程度和湍流动能增强,但流动结构稳定,压力波动的幅值较小。
第三,各级叶轮流道内和出口压力面附近的压力波动主要由叶轮和正导叶的动静干涉作用引起,为导叶叶频。叶轮出口中间位置和吸力面附近的压力波动易受到叶轮内不稳定流动的影响,波动主频为叶轮叶频。正、反导叶内为叶轮叶频,是叶轮和正导叶的动静干涉波动向下游传播的结果。
参考文献:
[1]祝卓华.多级离心泵常见故障问题与处理技术研究[J].内燃机与配件, 2019,(18):180-181.
[2]曹卫东,刘光辉,施卫东,等.多级离心泵内部非定常压力分布特性[J].农业工程学报, 2014,30(14):64-69.
[3]马新华,冯琦,蒋小平,等.多级离心泵内部非定常压力脉动的数值模拟[J].排灌机械工程学报, 2016,34(1):26-31.
[4]张玉良,李昳,崔宝玲,等.两相流离心泵水力输送性能计算分析[J].机械工程学报, 2012,48(14):169-176.
[5]Gandhi B K, Singh S N, Seshadri V. Performance characteristics of centrifugal slurry pumps[J]. Journal of Fluids Engineering, 2001,123:271-280.
[6]Satish Kumar, Gandhi B K, Mohapatra S K. Performance characteristics of centrifugal slurry pump with multi-sized particulate bottom and fly ash mixtures[J]. Particulate Science and Technology, 2014,32:466-476.
[7]史宝成,魏进家,邱伊婕,等.液固两相离心泵内固体颗粒对液相湍流调制的测试方法及机理[J].科学通报, 2018,63(11):1050-1061.
[8]黄先北,杨硕,刘竹青,等.基于颗粒轨道模型的离心泵叶轮泥沙磨损数值预测[J].农业机械学报, 2016,47(8):35-40.
[9]刘娟,许洪元,唐澍,等.离心泵内固体颗粒运动规律的实验研究[J].水力发电学报, 2008,27(6):168-172.
[10]汪家琼,蒋万明,孔繁余,等.固液两相流离心泵内部流场数值模拟与磨损特性[J].农业机械学报, 2013,44(11):53-60.
[11]夏密,李昳,李凤琴,等.固液两相流离心泵内颗粒运动规律的数值研究[J].机电工程, 2015,32(12):1555-1563.
[12]章城,徐圣永,吕兆聪,等.离心泵内部两相流模拟及其叶轮的流固耦合分析[J].南水北调与水利科技, 2015,13(3):506-509.
[13]黄思杰,邵春雷.输送多组分介质的离心泵内部固液两相流特性[J].农业工程学报, 2016,32(20):77-84.
[14]韩伟,金毅,李仁年,等.颗粒对离心泵内部压力脉动特性的影响[J].排灌机械工程学报, 2015,33(6):467-474.
[15]刘建瑞,徐永刚,王董梅,等.离心泵叶轮固液两相流动及泵外特性数值分析[J].农业机械学报, 2010,41(3):86-90.
[16]廖娇,赖喜德,廖功磊,等.基于固液两相流的离心泵内部流场数值分析[J].热能动力工程, 2017,32(5):95-99.
[17]曹卫东,刘光辉,施卫东,等.多级离心泵内部非定常压力分布特性[J].农业工程学报, 2014,30(14):64-70.
[18]马新华,冯琦,蒋小平,等.多级离心泵内部非定常压力脉动的数值模拟[J].排灌机械工程学报, 2016,34(1):26-31.
