帮你闯关辅助线（十）

张鑫

割补是指对原几何图形或几何元素进行切分、补足等操作，其作用是将原图形分割或补成相对独立或更为完整的图形，常要借助连接、截取、作平行、作垂直等手段实施. 下面举例介绍.

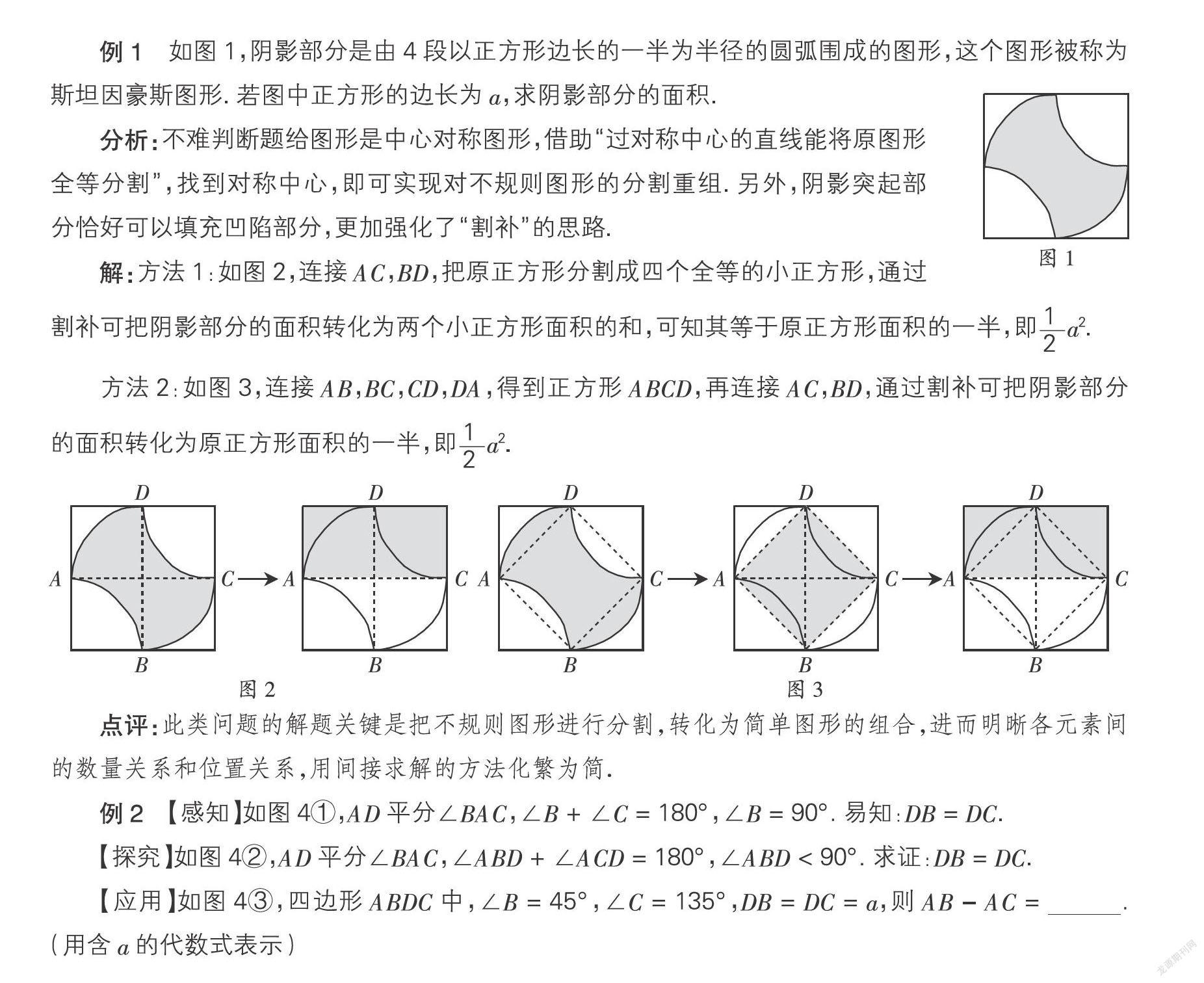
例1 如图1，阴影部分是由4段以正方形边长的一半为半径的圆弧围成的图形，这个图形被称为斯坦因豪斯图形. 若图中正方形的邊长为a，求阴影部分的面积.

分析：不难判断题给图形是中心对称图形，借助“过对称中心的直线能将原图形全等分割”，找到对称中心，即可实现对不规则图形的分割重组. 另外，阴影突起部分恰好可以填充凹陷部分，更加强化了“割补”的思路.

解：方法1：如图2，连接AC，BD，把原正方形分割成四个全等的小正方形，通过割补可把阴影部分的面积转化为两个小正方形面积的和，可知其等于原正方形面积的一半，即a2.

方法2：如图3，连接AB，BC，CD，DA，得到正方形ABCD，再连接AC，BD，通过割补可把阴影部分的面积转化为原正方形面积的一半，即a2.

点评：此类问题的解题关键是把不规则图形进行分割，转化为简单图形的组合，进而明晰各元素间的数量关系和位置关系，用间接求解的方法化繁为简.

例2 【感知】如图4①，AD平分∠BAC，∠B + ∠C = 180°，∠B = 90°. 易知：DB = DC.

【探究】如图4②，AD平分∠BAC，∠ABD + ∠ACD = 180°，∠ABD < 90°. 求证：DB = DC.

【应用】如图4③，四边形ABDC中，∠B = 45°，∠C = 135°，DB = DC = a，则AB - AC = . （用含a的代数式表示）

分析：角是轴对称图形，角平分线所在直线是其对称轴. 借助轴对称的观点处理角平分线问题，可以构造基于角平分线的全等三角形，实现边、角的等量位移.

解：【探究】（截长法）如图4②，在AB边上截取AE = AC，连接DE. ∵AD平分∠BAC，∴∠CAD=∠EAD，∵AD=AD，∴△ACD≌△AED，∴DC=DE，∠AED=∠C. ∵∠C+∠B=180°，∠AED+∠DEB=180°，∴∠DEB=∠B，∴DE=DB，∴DB=DC.

（补短法）如图4④，延长AC至点E，使AE = AB，连接DE. ∵AD平分∠BAC，∴∠EAD=∠BAD，∵AD=AD，∴△AED≌△ABD，∴DE=DB，∠AED=∠B. ∵∠ACD+∠B=180°，∠ACD+∠DCE=180°，∴∠DCE=∠E，∴DE=DC，∴DB=DC.

【应用】a.

点评：“截长补短”常被用来解决有关几何元素和、差、倍分的问题. 通过割补构造全等三角形是解决本题的关键.

例3 如图5，在直线m上摆着三个正三角形：△ABC，△HFG，△DCE. 已知BC = CE，F，G分别是BC，CE的中点，FM∥AC，GN∥DC. 设图中三个平行四边形的面积依次是S1，S2，S3，若S1 + S3 = 10，求S2.

分析：根据图形特点，可将图中的平行四边形分割成小等边三角形，或将小的平行四边形补成大的平行四边形.

解：方法1（分割法）：如图6①，将S1，S2，S3依次分成2个、4个、8个等边三角形，因为S1 + S3=10，所以S1=2，S3=8，即每个小等边三角形的面积为1，则S2=4.

方法2（补形法）：如图6②，延长BA，GH交于点P，显然菱形PACQ的面积等于S3， 而S2等于菱形PACQ的面积的一半，S1与阴影平行四边形同高，底是阴影平行四边形的一半，则S1=，所以S1∶S2∶S3=1∶2∶4，则易得S2=4.

点评：通过对图形的“割”或“补”充分体现几何图形的特征，发挥图形的优势来辅助计算是解决本题的关键.