基于Moran 过程的PPP 项目承包商机会主义行为演化动态

（太原理工大学 经济管理学院，太原 030024）

随着我国“一带一路”倡议的实行以及城镇化基础设施建设的推进，PPP 模式以其能够降低政府部门的债务、加强民营资本在建筑经济活动中的活力、提高项目的完成质量和效率而被广泛应用于我国建筑领域中。然而，在实际的运行与实施中，PPP 项目中也存在各种各样的问题。在PPP 项目中，政府部门与承包商目标不一致、信息不对称等问题十分普遍，使得在PPP 项目的全寿命周期过程中承包商采取机会主义行为这种现象的发生。针对PPP 项目中存在的承包商机会主义行为，提出有效的监管与治理对策，是政府亟待解决的问题。

一、文献综述

PPP 项目中的承包商机会主义行为受到社会广泛关注，学者纷纷对其展开研究。例如，Lohman 和Rötzel［1］研究了在PPP 项目中政府部门的行为会如何影响私人部门的行为，研究表明，政府部门的监管行为对私人部门的机会主义行为有抑制作用。尹贻林等［2］通过利用进化博弈理论，对业主行为的演化进行分析，对基于长短期合作下的进化均衡进行研究。为公共项目中怎样应对承包商机会主义行为寻求对策。通过研究发现，监管力度的增强带来的效果只能暂时性地降低损失，若要从根源杜绝这种现象的发生，需要考虑长期合作收益。张艳茹等［3］基于惩罚和补偿两种不同的机制，建构了进化博弈模型。通过对两种机制下进化稳定策略的分析，得到结论：对于抑制承包商的机会主义行为，相较惩罚机制，补偿机制更为有效。对于整治承包商机会主义行为在PPP 项目中较为普遍的现象，毕蕾［4］从契约的角度进行了研究，指出：治理双方契约的有效途径是互惠政策、信任机制与声誉机制。目前关于PPP 项目中承包商采取机会主义行为的研究大多都是运用演化博弈的方法，在这种模型下参与方通常是无限的或者足够多的。然而在实际生活中，大多数演化行为都是在有限群体中进行的。本文拟在PPP 项目中承包商数量有限的条件下，研究承包商策略选择及影响因素。

博弈论是对策略选择进行研究不可或缺的方法。演化博弈论是基于参与方有限理性与信息不完全的角度分析参与方策略的选择机制，“复制动态方程”和“ESS”是该模型的两个关键点。经典的演化博弈模型总是运用与个体无限的情形中。有限个体的演化一般都是随机过程。Taylor 等［5］讨论了有限个体的演化动态与经典的演化博弈模型中的无限总体复制动态之间的关系。柴彩春等［6］分析了制造商生产策略的演化动态，借助Moran 过程，得出了策略占优条件以及影响策略占优的因素。杨丰梅等［7］为了研究电商平台共享机制演化动态，借助了Moran 过程，分析得出电商共享策略占优的条件。王先甲等［8］借助Moran 过程研究了消费者众筹策略的演化动态，得出了在不同选择条件下推动消费者参与众筹的有利条件。

综上，本文是在PPP 项目中承包商个体数量有限的条件下，在考虑政府的惩罚、承包商的寻租行为、承包商举报成本等因素的条件下，借助Moran 过程探究不采取机会主义行为策略的占优条件。

二、模型假设

考虑单种群问题，假设在一个PPP 项目中有N个承包商，并且他们之间是无差异的，策略Y：承包商采取机会主义行为，策略S：承包商不采取机会主义行为，这是承包商的两种策略选择。假设在每一次博弈中，根据合同约定，承包商可获得固定收益R，采取机会主义行为策略的承包商所需的建设成本为C1，不采取机会主义行为策略的承包商所需的成本为C2，其中C1＜C2。当承包商一方采取策略S，另一方采取策略Y时，采取机会主义行为策略的一方以概率β对不采取机会主义行为策略的一方进行贿赂，并支付寻租成本B；而不采取机会主义行为策略的一方以概率α 举报采取机会主义行为策略的一方，并需承受相应的举报成本D。假设若双方都存在机会主义行为，则会被政府发现并进行相应的罚款P。假设任何一方都无法逃脱相应的处罚。其中，α、β取值为0～1。

根据以上假设与阐述，策略S与策略Y的支付矩阵见表1。

表1 PPP 项目中承包商1 和承包商2 的支付矩阵

其中，R＞0：承包商按合同约定所取得的固定收益；C1＞0：承包商存在机会主义行为所需的建设成本；C2＞0：承包商不采取机会主义行为时的建设成本；P＞0：机会主义行为，被政府发现后，政府对其的罚款；B＞0：承包商之间互相贿赂（寻租）的成本；D＞0：承包商若发现另一个承包商采取机会主义行为时进行举报的成本；α∈［0，1］：承包商举报他人的概率；β∈［0，1］：承包商进行贿赂（或寻租）的概率。

下面，基于Moran 过程研究无差异的N个承包商在两种策略下的演化动态。

三、Moran 过程模型

在有限总体中，研究个体选择问题常常借助经典的遗传学模型——Moran 过程。在相同步长的时间段内，复制产生一个相同的个体，个体被选择的依据是策略的适应度，同时随机替换剩余的N-1 个个体中的一个，从而保持总体数目N不变。假设群体中承包商的数量是N，i是不采取机会主义行为策略S的人数，则采取机会主义行为策略Y的人数为N-i，承包商采取策略S和策略Y的期望收益［9］分别为：

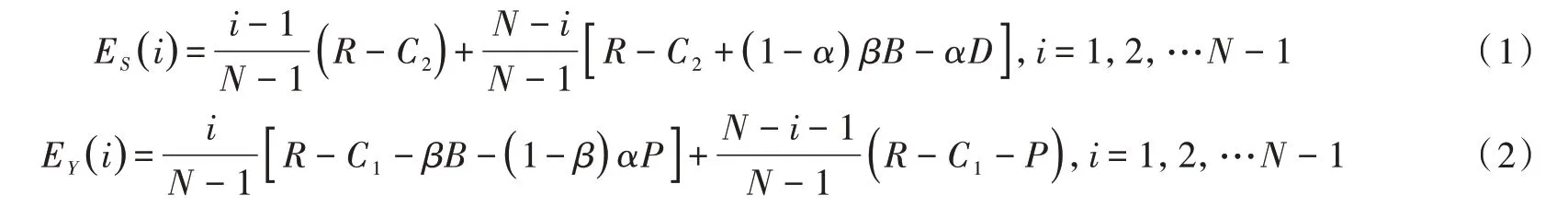
假设适应度为期望收益的线性函数，则式（3）、式（4）分别为策略S和策略Y的适应度：

其中：ω为选择强度，其取值范围为［0，1］。

基于Moran 过程［10］展开分析，可以得出为采用策略S的个体增加1 个的概率，策略S的个体数量随着时间步的演化，可能会增加、减少或者不变。因此，Moran 过程的概率转移矩阵是一个除了对角线元素以外，其余元素均为零的三对角矩阵。对角线元素为

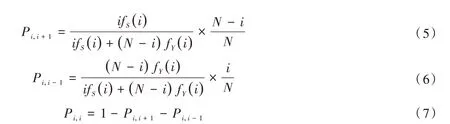
所有承包商都采取机会主义行为策略，即i=0，或都不采取机会主义行为策略即i=N，这是Moran 过程的两个稳定状态。若总体呈现出这两种状态之一，将保持这种状态稳定不变。下面计算总体分别达到这两种状态时的扎根概率。

令xi表示初始状态为有i个个体采取S策略，然后演化到S策略被全部N个个体采取的概率。由全概率公式可得：

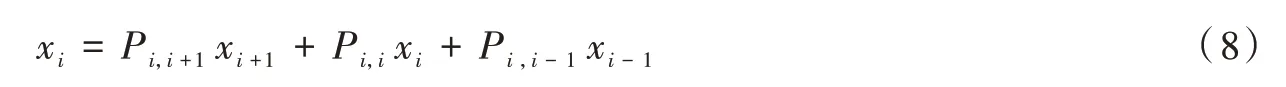
边界值x0=0，xN=1，将Pi，i+1，Pi，i，Pi，i-1的表达式带入式（8）中，可解得

当考虑只有一个承包商采取S策略时，其余N-1 个承包商均选择采取Y策略，最终S策略稳定的概率为

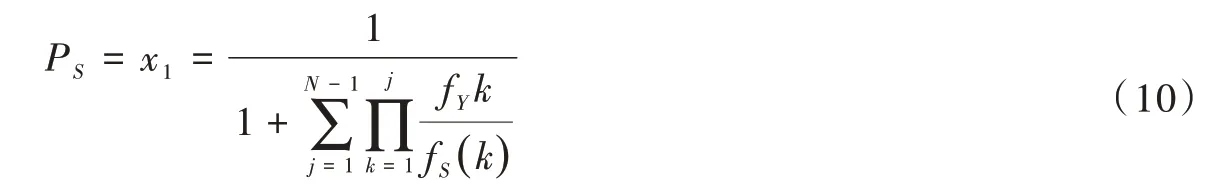
当只有一个承包商采取Y策略，其余N-1 个承包商均采取S策略时，最终Y策略稳定的概率为

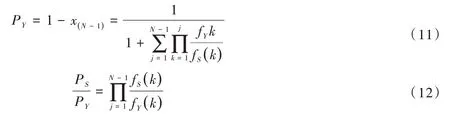
两种策略扎根概率的比例如式（12）所示，当无变异时，经过足够长时间的演化，最终的稳定策略更可能是扎根概率较大的一方。

当式（12）大于1，即PS＞PY时，当策略无变异时，采取策略S的扎根概率较大，经过长时间的演化，逐渐增加的策略S的个体数量，会使得演化稳定策略为承包商不采取机会主义行为。

四、结果分析

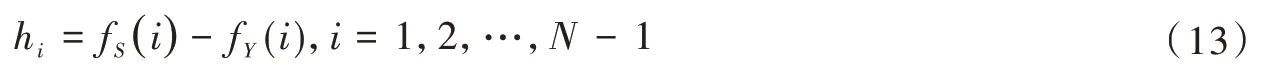
若h1＞0，表示支持策略S入侵策略Y；若hN-1＜0，表示策略Y侵入策略S更易。

1.强选择性下的演化动态

强选择条件下，ω=1，此时承包商的策略只与其期望收益有关，与其他外界因素无关。

故此时，fS(i)=ES(i)，fY(i)=EY(i)

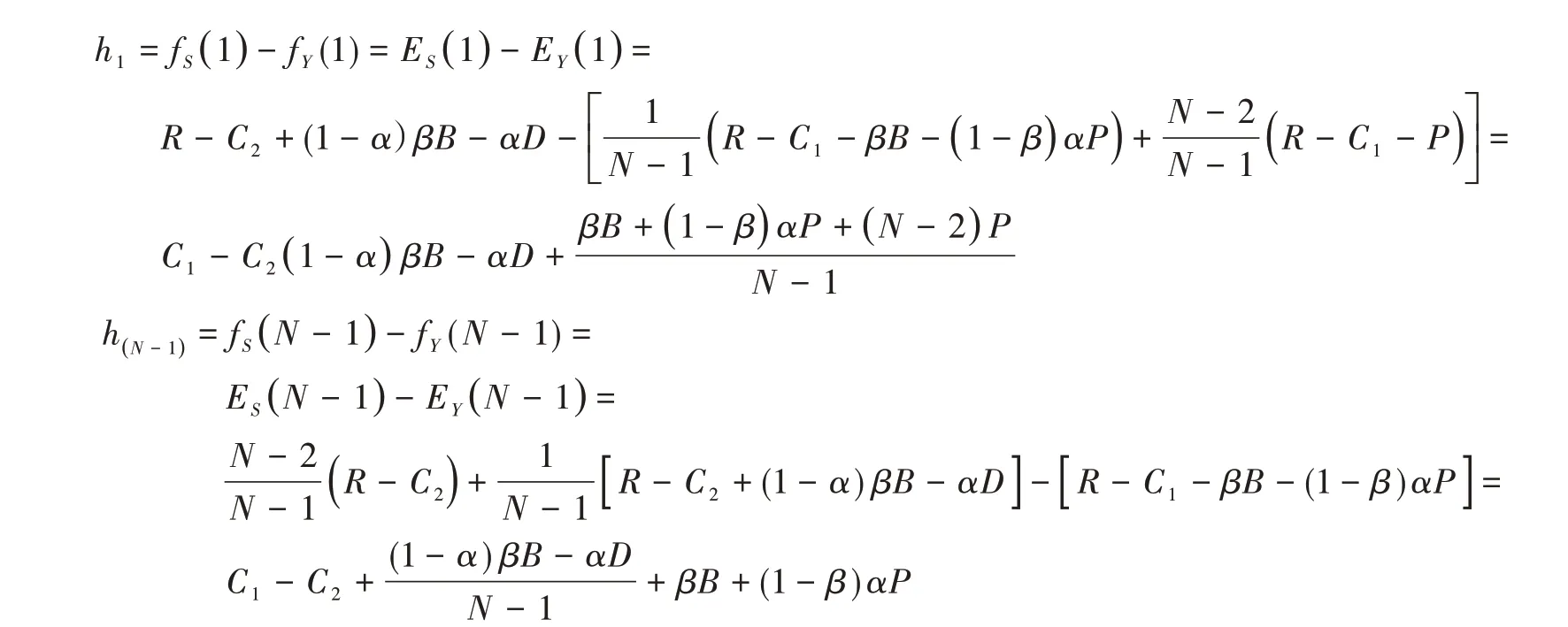
命题1：当时，h1＞0，h（N-1）＞0。此时，演化的结果为有利于S策略入侵Y策略，即趋向于不采取机会主义行为。

2.弱选择性下的演化动态

对于承包商在弱选择性条件下采取策略的适应性，未来期望收益不是唯一的影响因素，可能还会考虑自身的声誉问题以及长期合作机会等因素的影响。在弱选择性条件下，ω→0。将PS在ω→0 时根据泰勒展开式［11］展开，可得到：

综上分析，根据Moran 过程的扎根概率，分析得到策略S的占优条件，在承包商数量较多时，一方面可以通过降低不采取机会主义行为的承包商对采取机会主义行为承包商的举报成本，推动来自承包商内部的互相监督；另一方面可以通过增强对采取机会主义行为的承包商的惩处力度，来减少机会主义行为的发生。

五、数值分析

借助数值实验对随机演化模型进行以下分析，从而对不采取机会主义行为策略演化的影响因素进行分析。包括不采取机会主义行为策略的承包商对采取机会主义行为策略的承包商的举报成本D和总包对采取机会主义行为策略的承包商的惩罚P。

不失一般性，考虑不同的选择强度ω下不采取机会主义行为策略演化率r=NPS与承包商总数N的关系。为简化符号，以下记为

ɑ=R-C2，b=R-C2+(1-ɑ)bB-ɑD，c=R-C1-bB-(1-b)ɑP，d=R-C1-P。如图1 所示（取ɑ=4，b=4.08，c=5.42，d=3），可知演化率r是承包商总数N的单峰函数，当n值很小时，有NPS＜1，即稳定策略为承包商采取机会主义行为；当n增大到一定范围内，无论选择强度ω多大，均有NPS＞1，即承包商不采取机会主义行为策略S会成为稳定状态；对于N→∞，若要保持NPS＞1，选择强度ω有一定的阈值，较小的ω取值使得稳定策略为承包商不采取机会主义行为。

第4 部分对ω→0 的情形，进行了理论论证及结果分析。现算例部分考虑ω=1 的情形下，最终稳定状态受到各种因素影响的情况。

（1）在其他参数保持不变的条件下，考虑参数D即举报成本对最终稳定状态的影响。如图2 所示，逐渐降低举报成本分别得到曲线r1（取ɑ=8，b=1，c=2，d=4）；r2（取ɑ=8，b=1.8，c=2，d=4）；r3（取ɑ=8，b=2.6，c=2，d=4）；r4（取ɑ=8，b=3.4，c=2，d=4）；r5（取ɑ=8，b=4.2，c=2，d=4）。从图2 中的变化趋势可以看出，降低承包商的举报成本，会使最终的稳定策略逐渐演化为承包商不采取机会主义行为。

（2）在其他参数恒定的情形下，考虑参数P即总承包商对采取机会主义行为策略的承包商的惩罚力度对最终稳定状态的影响。如图3 所示，逐渐增加惩罚力度，分别得到曲线r1（取ɑ=10，b=4，c=10，d=8）；r2（取ɑ=10，b=4，c=7，d=6.5）；r3（取ɑ=10，b=4，c=5.5，d=4.5）；r4（取ɑ=10，b=4，c=4.5，d=4）；r5（取ɑ=10，b=4，c=4，d=3.5）。从变化趋势上可以看出，较弱的惩罚程度会使得占优策略为承包商采取机会主义行为，随着惩罚程度的增大，承包商不采取机会主义行为成为进化稳定状态。

根据图1～图3 可以看出，ω=1 即只有博弈收益决定适应度时，降低不采取机会主义行为策略的承包商对采取机会主义行为策略的承包商的举报成本和加大总包对采取机会主义行为策略的承包商的惩罚力度，将会使最终稳定状态是承包商不采取机会主义行为。

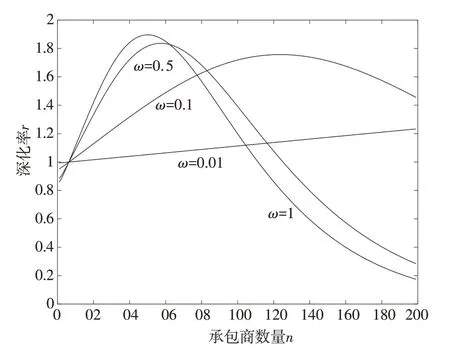
图1 不同选择强度下承包商总数与不采取机会主义行为演化率关系图

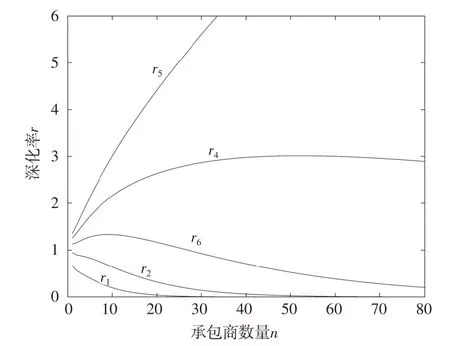
图2 不同举报成本下承包商总数与不采取机会主义行为演化率关系图

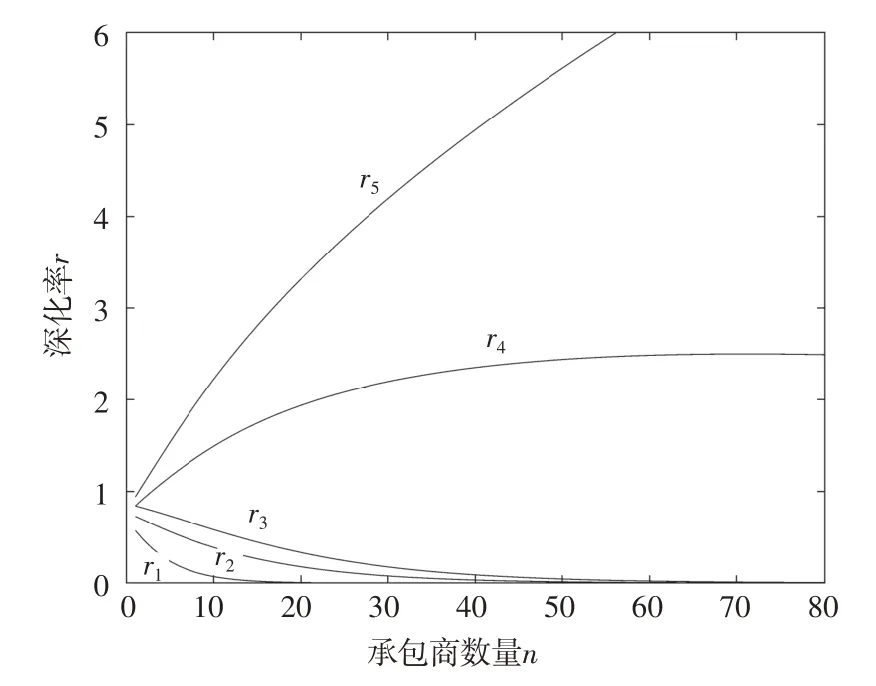
图3 不同惩罚程度下承包商总数与不采取机会主义行为演化率关系图

六、结论

本文研究了在承包商数量有限的条件下，PPP 项目中研究承包商不采取机会主义行为策略的演化趋势。基于演化博弈理论，引入Moran 过程，并借助随机过程中的马尔科夫转移矩阵法，运用概率转移矩阵，计算了承包商是否采取机会主义行为策略的扎根概率。以中性入侵概率作为比较标准，若PY大于中性入侵概率，则受自然选择的影响，机会主义行为策略的承包商会逐渐侵占整个群体；若PS大于中性漂变概率，则承包商采取机会主义行为策略会被抵抗，而不采取机会主义行为策略的承包商会逐渐取代采取机会主义行为策略的承包商。最后，分析了两策略在强弱选择性强度下占优的条件，并通过数值算例进行验证，进而得到相应的管理建议：PPP 总承包商可以通过增加承包商的数量，应用互联网技术建立新型的监管平台，降低承包商间的举报成本，同时加大惩罚力度，从而减少PPP 项目中承包商的机会主义行为。