基于相似日的PSO-ELM算法的短期负荷预测研究
2020-09-10李娜
李 娜
(太原工业学院 自动化系,山西 太原 030008)
0 引言
精确的短期负荷预测对于优化居民、节能减排具有重要的参考价值[1]。短期的负荷预测用于预测下一天的负荷值。每天的负荷具有周期性,主要体现在不同日的日负荷曲线其整体规律和同一星期类型日负荷规律相似[2]。基于负荷的这个特点,本文提出的负荷预测方法是通过选取相似日作为样本,用粒子群-极限学习机(PSO-ELM)方法进行预测下一天负荷值。首先利用聚类分析方法选取相似日,将相似日进行小波分析,对其中的周期性数据,利用PSO-ELM进行负荷,然后将预测结果与分周期性结果加权求和,并利用欧洲智能技术网络竞赛1997负荷数据进行验证。结果表明,该方法预测精度高,而且稳定。
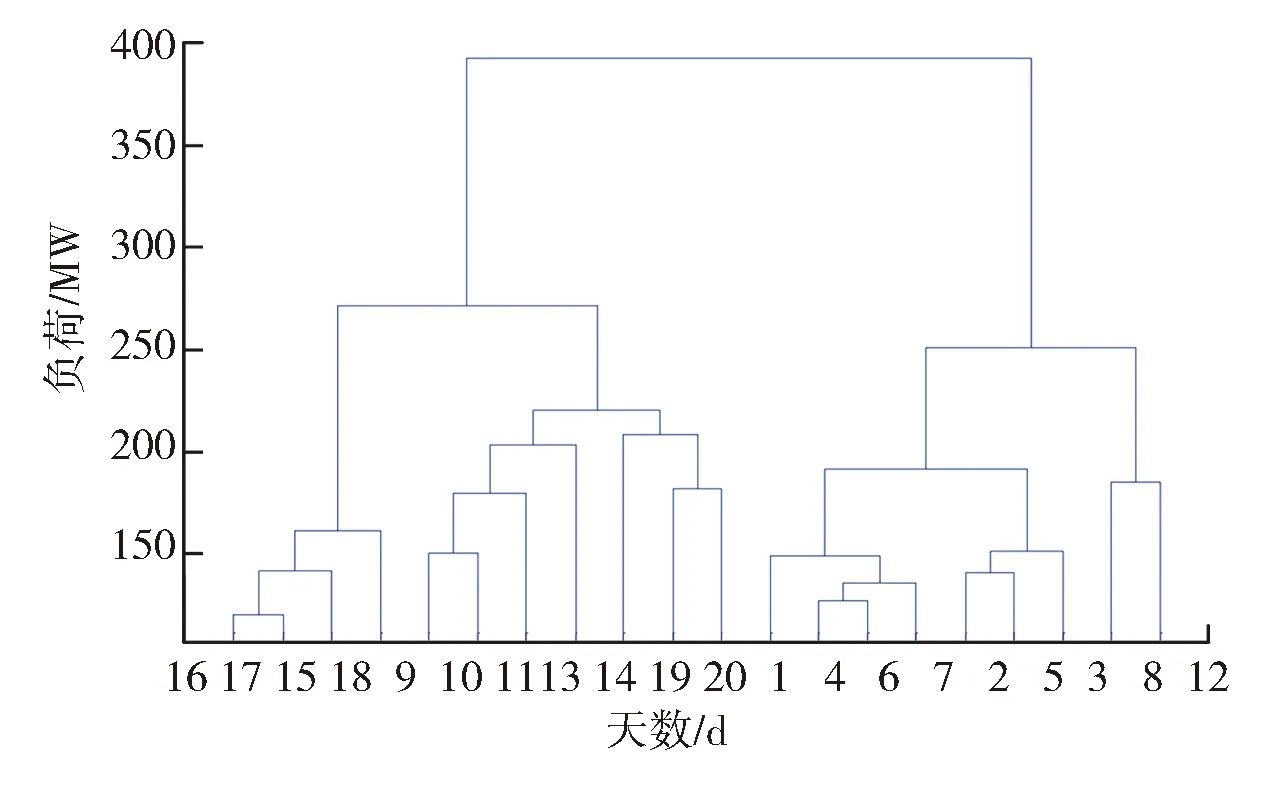
图1 聚类分析结果图Fig.1 Cluster analysis results
1 相似日的选取
经济、天气、日期的类型等影响负荷的大小,并且相似的日期类型负荷大小比较相近,因此本文利用负荷曲线的相似度来选取相似日,以待预测日一周数据,前7 d数据、前14 d数据、前21 d数据,以此类推得到相似日的候选日,利用负荷曲线的距离来进行聚类分析,从聚类结果中找到与预测日最近的历史日[3]。
本文算例中聚类分析结果如图1所示。相似日为3月2日、3月9日、3月16日、3月30日、3月31日、4月5日。
2 极限学习机预测模型
ELM是由Huang等人于2006年提出来的,与神经网络相比,它是单隐层的前馈神经网络,该方法的目的是训练误差值最小,隐含层不需要迭代,并且输入的权值和偏置值可随意选取, 待输出的权值计算出来,算法的参数即可确定。 ELM的算法模型如图2所示[4]。
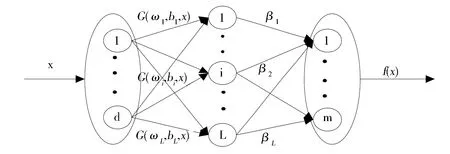
图2 ELM模型图Fig.2 ELM model diagram
ELM算法可以总结为[5-7]:
2)确定输入的权重ωi和隐含层的偏差bi的数值。
3)计算隐含层的输出矩阵H。
(1)
4)根据输出矩阵得到输出权值矩阵β:β=H+T,其中H+是Moore-Penrose广义逆矩阵。

(2)
3 PSO-ELM负荷预测模型
3.1 改进粒子群算法
由于输入的权值ωi和隐含层的偏差bi的数值是随机的,所以ELM算法的稳定性和快速性受到影响。因此本文采用PSO算法确定ELM算法中输入的权值和隐层的偏置值,PSO算法通过对鸟群觅食行为的研究提出的一种群体智能优化算法,是一类随机全局优化技术,所需参数少。每个个体最优数值和全局的最优数值随着粒子的位置更新产生,迭代的公式为[8-11]:
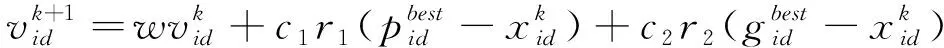
(3)
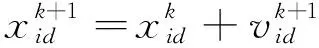
(4)
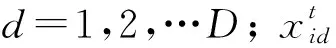
为了防止PSO算法进入局部的收敛和解决收敛速度过快等问题,本文对惯性的权重系数值进行了改进:
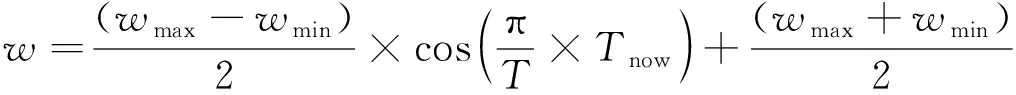
(5)
其中:wmax、wmin分别是最大惯性权重系数和最小惯性权重系数;T是给定的更新迭代次数值;Tnow是现在的更新迭代次数值;cos函数的取值范围为[0,π]。在PSO算法的前期,寻优速度减小的比较慢,粒子群以比较大的速度值寻取最优解,使粒子不易很快地进入局部的最优值中。在PSO算法的后期,粒子用较慢的速度值在解的空间域中搜索,能够较快速找到全局的最优值。
3.2 PSO-ELM参数优化
综上可得,PSO-ELM的参数确定如下:

图3 基于相似日的PSO-ELM负荷预测流程图Fig.3 Flow chart of PSO-ELM load forecasting based on similar days
1)用ELM算法中随机选定的输入的权值和隐层的阈值作为粒子群的数值,然后确定种群的大小,迭代的次数,初始的权重值和加速系数值。
2)确定每个粒子适应度大小,即ELM算法的预测值与样本数据的均方根。

(6)
3)采用式(4)更新粒子的位置,得到新的粒子适应度数值,并保存种群中最优个体位置和全局的最优位置值。
4)判断是否满足了终止条件或者达到更新迭代次数的数值,是则退出循环,并返回保存最优个体解,即确定了最优的权值和阈值,否则继续循环步骤3。
5)采用PSO的粒子数值,作为ELM算法的初始的输入权重值和隐含层的阈值。
3.3 负荷预测模型流程
基于相似日的PSO-ELM负荷预测流程如图3所示。
4 算例分析
本文利用1997年欧洲智能技术网络竞赛中前95 d的负荷作为原始数据,预测第96 d的48个节点的负荷值,来验证本文所提方法的可行性。
原始负荷曲线图和小波分解序列如图4和图5所示。

图4 原始数据序列图Fig.4 Original data sequence diagram

图5 小波分解序列图 Fig.5 Wavelet decomposition sequence diagram
由图5可以看出,原始数据包含有周期分量和细节分量,其中a3为周期分量,对其利用PSO-LEM进行负荷预测,得到结果如图6所示。
由图6可以看出,预测结果与周期性负荷走向趋势一致,表明了预测结果具有可信性。将预测结果与细节分量加权求和,得到最终的负荷预测结果如图7所示。
为了同ELM算法的预测结果进行比较,本文选用均方根误差,平均相对误差和最大误差三种指标,实验结果如表1所示。

表1 两种算法的误差对比Table 1 Comparison of errors between the two algorithms
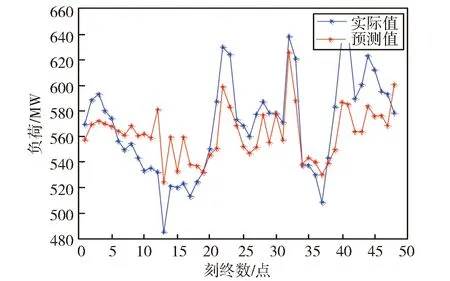
图6 周期性分量负荷预测结果Fig.6 Periodic component load forecasting results

图7 最终负荷预测值Fig.7 Final load forecast
5 结论
由实验结果可知,本文所采用的基于相似日的PSO-ELM算法的负荷预测方法,在均方根误差、平均相对误差和最大误差三种评价指标方面均优于ELM负荷预测方法,提高了短期负荷预测的预测精度。因此,本文提出的方法具有较好的适用性,适用于电力系统的短期负荷预测。但是程序运行时间较长,因此在最优参数搜索方面还需进一步研究。
