计及弯折波的舰载飞机偏心拦阻动力学分析

谢朋朋，彭一明，魏小辉，*，聂宏

（1.南京航空航天大学 机械结构力学及控制国家重点实验室，南京210016；2.南京航空航天大学 飞行器先进设计技术国防重点学科实验室，南京210016； 3.上海卫星装备研究所，上海200240）

舰载飞机的设计必须满足与航空母舰的适配性要求［1］。舰载飞机的设计首先必须考虑在有限空间的起降问题［2］，就“降”的问题，拦阻着舰一般分为5个阶段：进场、触舰、机轮压索、拦阻钩挂索和舰载飞机拦停。在舰载飞机拦阻着舰过程中，飞机沿一定的下滑轨迹角进场［3-5］，在极短的时间内短距离内被拦停。

国外在拦阻方面进行了大量的飞行试验并公布了相关的试验结果曲线，试验报告大多只提及了舰载飞机无偏心状态下的对中拦阻情况，在偏心拦阻方面仅仅公布了极少量的实测数据的拟合曲线，而对于偏心拦阻的机理以及理论分析鲜有公开。

近年来，国内对拦阻装置的理论研究较为全面，但是对拦阻动力学特性的理论研究和仿真分析还不够完善。拦阻动力学特性的相关研究多是用简化的弹簧线性力或是将美国军用标准ADA119551［6］和MILSTD-2066［7］中对应力值曲线作为输入，且对舰上拦阻部分（即拦阻索以及拦阻机）进行了简化。张澍森和金栋平［8］对拦阻系统中飞机动力学进行了优化分析，金长江和洪冠新［9］建立了飞机着舰动力学模型。在偏心拦阻方面，张鑫和李玉龙等［10］对偏心拦阻钩索动力学进行了分析，侧重于不同质量的飞机着舰的对比。张卓坤等［11］对偏心拦阻的结果趋势进行了分析，孟祥印［12］对偏心拦阻时钩索后减速过程进行了简要描述，段萍萍［13］对非对称拦阻进行了力学分析并对不同偏心率下的拦阻性能进行了分析。在这些研究中均忽略了弯折波对于拦阻动力学特性的影响，实际上，舰载飞机拦阻过程初期拦阻索中会出现波动现象，当横波在钩-索啮合点和甲板滑轮之间往复传播与反射时可导致拦阻索发生弯折，进而影响拦阻索拉力。

通常，对于舰载飞机拦阻的试验或理论研究主要集中于对中拦阻过程，计及弯折波的研究也以研究对中拦阻过程为主［10，14-16］，计及弯折波的偏心拦阻动力学研究少有学者涉及。本文基于离散方法的弯折波模型，建立了拦阻动力学模型并验证了模型的准确性，在此基础上对偏心拦阻过程进行了仿真计算，分析了不同偏心度对弯折波、拦阻索拉力以及拦阻动力学特性的影响。

1 舰载飞机拦阻动力学模型

舰载飞机拦阻系统示意图如图1所示。舰载飞机按照既定方式进场后，拦阻钩作为连接飞机与道面的桥梁，将拦阻力传递到机身上，从而强制飞机迅速减速，一般3 s内被拦停在安全区域内。因此，舰载飞机挂索后的减速运动特性是决定甲板长度设计的最重要因素之一［12］，同时也是决定拦阻安全特性的重要因素。

挂索后飞机的受力状态比较复杂，在拦阻过程中拦阻钩与跑道上制动拦阻索相啮合，拦阻索通过拦阻带与跑道两侧的拦阻机联结，拦阻索在拦阻机提供的张紧力作用下迅速回弹，从而将拦阻力传递到飞机上，因此对舰载飞机着舰挂索之后短时间内拦阻机提供的拦阻力进行计算分析极其重要。

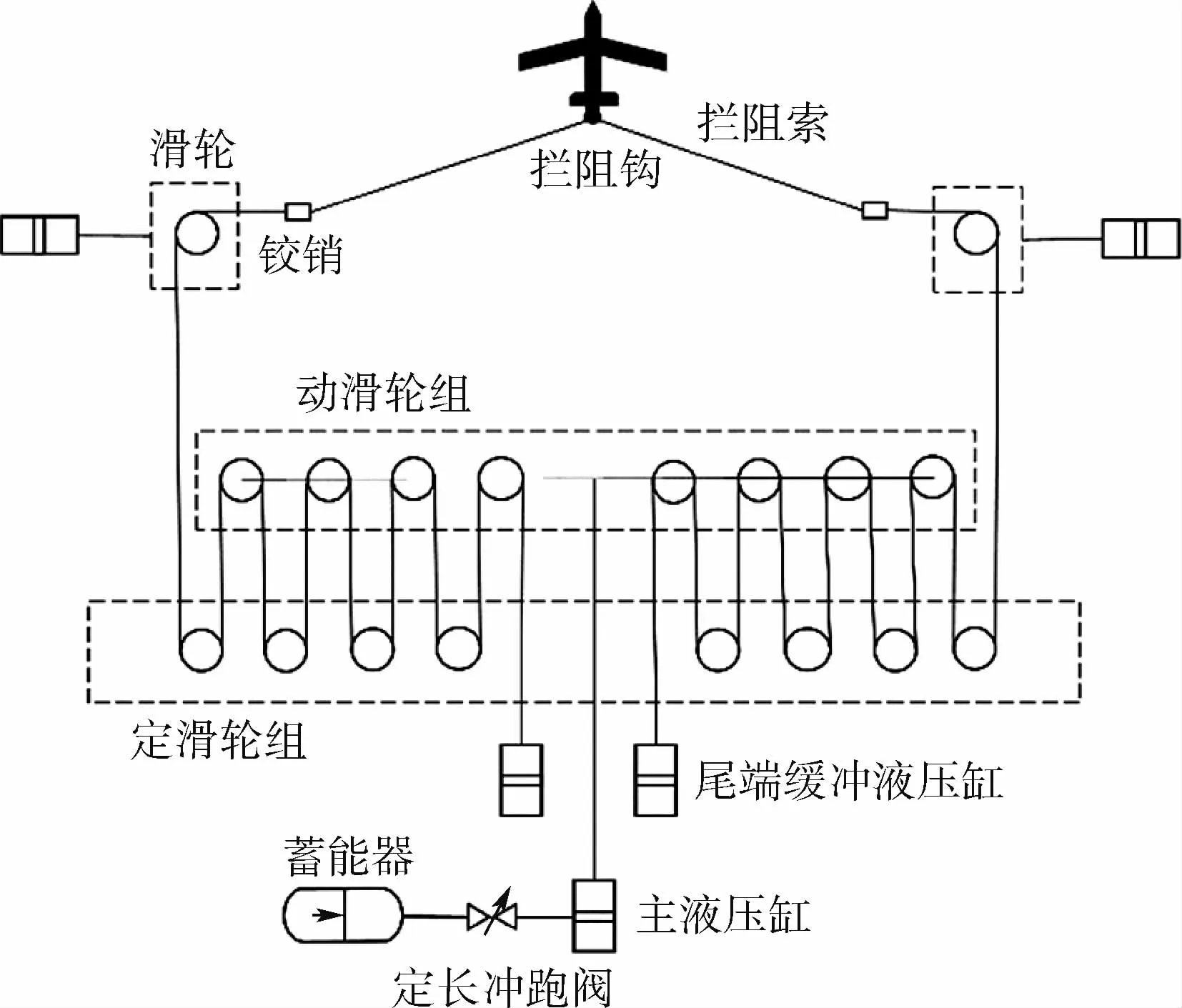
图1 舰载飞机着舰挂索示意图Fig.1 Schematic diagram of landing and cable hanging of carrier-based aircraft

1.1 舰载飞机拦阻力模型

由于舰载飞机在着舰拦阻过程中受力极其复杂，为便于分析，对着舰过程中飞机的受力情况作如下简化［17］：

1）跑道为平面，飞机航向与道面平行。

2）拦阻过程中，暂不考虑钩索啮合后的振动，忽略拦阻钩与拦阻索之间的摩擦力。

3）不考虑舰载飞机着舰垂直高度对拦阻力的影响。

在对中拦阻（不考虑偏心偏航）时，舰载飞机所受拦阻力如图2所示，A点为左侧甲板滑轮与拦阻索啮合点，B为右侧甲板滑轮与拦阻索啮合点，O为两者中点。

图2 拦阻力示意图Fig.2 Schematic diagram of arresting force

由图2可得拦阻力计算公式为

式中：Fx为作用于舰载飞机上的拦阻力；TL为左侧拦阻索拉力，TR为右侧拦阻索拉力，对中拦阻时两者相等；β为钩索啮合点和滑轮连线与航向的夹角；S为舰载飞机位移；D为甲板两滑轮间距的一半。

当偏心拦阻时，以右偏心ΔD为例，舰载飞机偏心拦阻受力情况如图3所示。

由图3可得拦阻力计算公式为

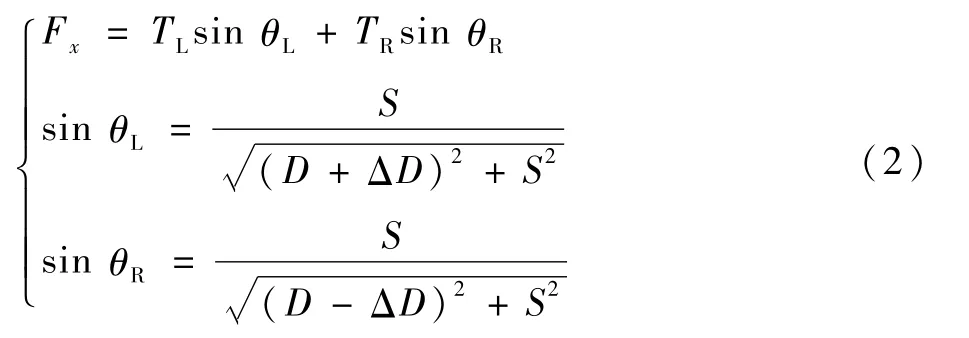
式中：θL为左侧拦阻索与两滑轮连接线夹角；θR为右侧拦阻索与两滑轮连接线夹角。

图3 偏心拦阻示意图Fig.3 Schematic diagram of off-center arrest

1.2 拦阻装置计算模型

要计算拦阻力，需要得到拦阻装置吸能器输出的阻尼力的变化规律，其与斜向流量控制阀的运动位移、阀上油槽截面积变化规律和蓄能器内压强有关［18］，吸能器的工作原理如图4所示。

图4 拦阻装置吸能器工作原理Fig.4 Working principle of arresting gear energy absorber

偏心拦阻与对中拦阻主要区别在于：拦阻钩左右的拦阻索初始长度存在差异导致左右滑轮带出的阻拦索长度不一样，最终导致两边活塞位移和速度不一样。对于某一确定的拦阻系统，其输出的拦阻索拉力与控制阀柱塞行程有关，当被拦阻飞机质量不变时，相同的索伸长量即对应相同的拦阻索拉力［19］。

对中拦阻时，活塞的位移量和运动速度分别为

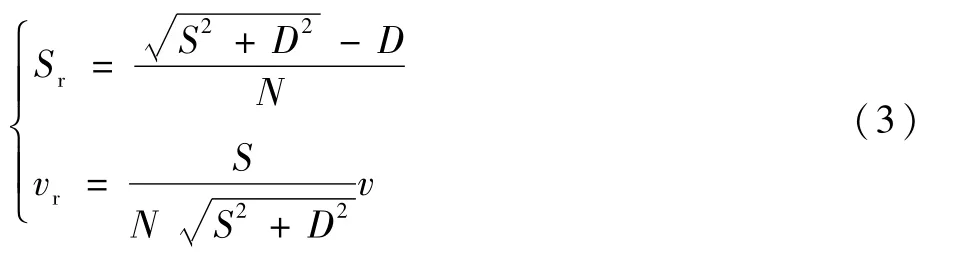
式中：N为动滑轮组中的动滑轮的个数；v为飞机的运动速度。

右偏心ΔD时：

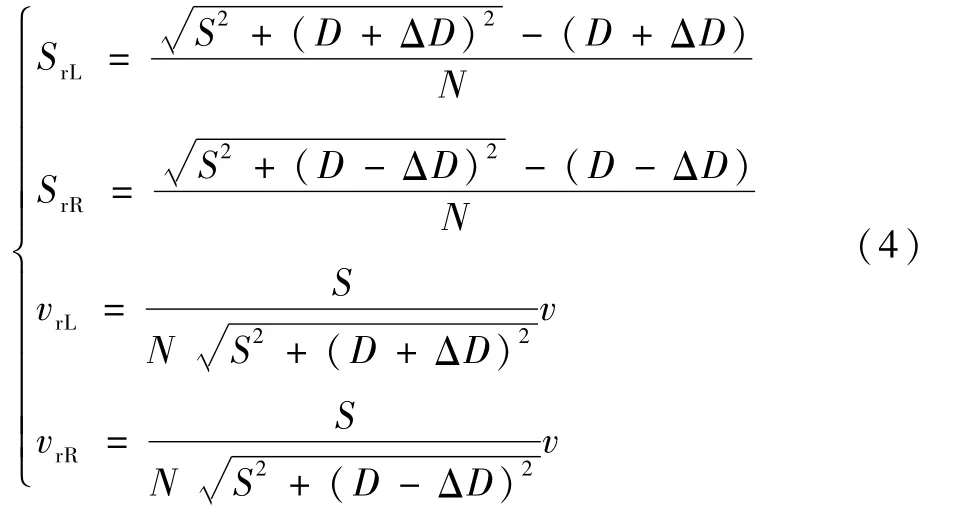
式中：SrL为左侧活塞的位移量；SrR为右侧活塞的位移量；vrL为左侧活塞的运动速度；vrR为右侧活塞的运动速度。

2 弯折波传播计算模型

拦阻索在受到拦阻钩冲击之后，会在其中产生弯折波，包括横波和纵波，绳索在2种波的作用下会发生弯折［20］。拦阻前期由弯折波起主要作用，本文使用离散的弯折波模型，该模型认为应力波引起的弯折第一次传播到滑轮后立即在钩索啮合处激发第二重弯折波，之后类似产生第三重弯折波［21］。在整个拦阻过程中，弯折波对拦阻载荷的影响逐渐减弱，随着拦阻机阻尼力逐渐增加，弯折波的影响迅速降低，因此整个拦阻系统模型只需考虑前三重弯折波［15］，之后飞机拦阻过程进入全液压阻尼力作用阶段。

弯折波本质上是一种冲击应力波［20］，当其在索中传播在弯折点到达左右滑轮前，拦阻机不起作用，因此研究弯折点的运动极其重要。

垂直撞击时，绳索中的应力可以近似看成只与冲击速度有关，在这种情况下的弯折波速度［14］为

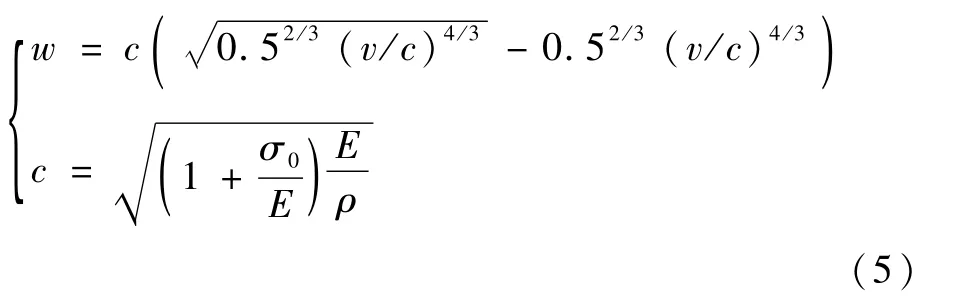
式中：w为弯折波速度；c为纵波波速；v为钩索初始接触速度；σ0为冲击前索中初始应力；E和ρ分别为拦阻索的弹性模量和密度。

在建立弯折波模型以及拦阻系统模型的过程中，采用了如下简化：

1）拦阻钩与拦阻索之间没有相对滑动。

2）不考虑拦阻钩在垂直方向上的分力。

3）在任意时刻，拦阻钩任一侧的拦阻索拉力处处相同。

4）假设拦阻索是材料一致的同一种钢索。

5）在拦阻过程中拦阻索处于线弹性范围。

对中拦阻时的拦阻索形式如图5所示。

图5 对中拦阻时拦阻索形式Fig.5 Form of arresting cable in centering arrest

设t时刻拦阻索一侧构型如图5所示，以O为原点建立坐标系。图中（xw，yw）为弯折点Q的坐标、（x，y）为飞机的实时坐标，（¯x，¯y）为上重弯折波结束时的飞机坐标，l1和l2分别为拦阻钩到弯折点和弯折点到滑轮的拉索长度，lw为该重弯折波经过的路程。

由图5可得

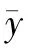
偏心拦阻时（右偏心ΔD）的拦阻索形式如图6所示。

实际在偏心拦阻前期，因拦阻力的作用舰载飞机可能会出现偏航角，但前三重弯折波作用期间时间极短，大约零点几秒，为便于计算认为飞机在前三重弯折波作用期间偏航角始终为0°。

在计算弯折波时，采用Euler法中的梯形公式，在仿真步长取得足够小时可以保证收敛。假设上一时刻飞机加速度、速度和位移为a0、v0、S0，当前时刻的飞机加速度、速度和位移为a1、v1、S1，取时间步长Δt=0.000 1 s，则有

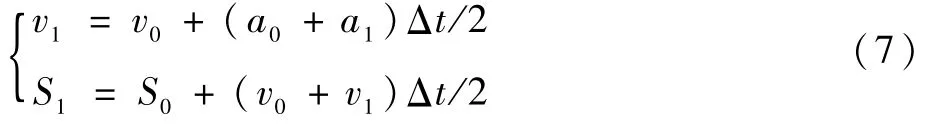
具体求解过程为：先由式（5）得到弯折波速度，代入式（6）即可得到左侧弯折点坐标（xwL，ywL）、右侧弯折点坐标（xwR，ywR）和两侧各段索长度。

由胡克定律可得任一侧拦阻索的张力为

图6 偏心拦阻时拦阻索形式Fig.6 Form of arresting cable in off-center arrest

式中：q为拦阻索的横截面积；l为单侧拦阻索总长；δ为单侧拦阻索伸长量；z为单侧动滑轮组移动量。

进而可求得拦阻钩作用于飞机上的拦阻力，即钩载：

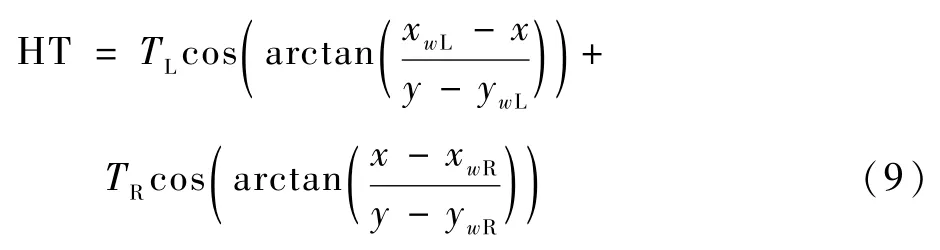
式中：TL、TR分别为左右两侧拦阻带拉力；HT为钩载。

在不同重的弯折波中，两侧初始时刻、初始弯折角不同，使得一些长度的计算公式不同，因此建立一个弯折波的连续模型来描述整个拦阻过程具有很大难度［14］。本文用离散的方法建立模型，采用时域逐步积分算法进行迭代计算，这样初始状态是已知的，整个求解模型随之确定。

3 模型校验

3.1 模型求解流程

前三重弯折波计算结束之后，拦阻进入全液压阻尼作用期间，在此期间使用Simulink搭建拦阻力计算模型，模型采用ode113求解器。该求解器为变步长求解器，在误差容限比较严时精度较高。设置相对误差容限为1×10-4，最大步长为0.001 s。输出此时的状态变量（飞机的位移和速度、左右两侧拦阻索与初始位置的夹角、两侧活塞的位移和速度等），继续进行拦阻过程的动力学计算，直至飞机停下，仿真结束。模型求解的具体流程如图7所示。

3.2 模型验证

为进行比较验证，以国外普遍使用的MK7-3型舰载飞机拦阻装置为例进行计算，模型计算参数［22］如表1所示。

对中拦阻时，拦阻力随位移变化曲线如图8所示。由图8可知，计及弯折波时拦阻力在初始阶段出现了明显的波动现象，说明拦阻索中弯折波的效应是不可忽略的。

图9为仿真与试验拦阻力随位移曲线的对比，美国军用标准MIL-STD-2066［7］提供的拦阻力随位移的变化规律进行了归一化处理，为方便对比验证，使用同样的方法对对中拦阻的计算结果进行归一化处理。从2组数据的对比结果可以看出，拦阻力在初期阶段受弯折波影响出现波动现象与试验数据基本一致，载荷波动是应力波在甲板滑轮与钩-索啮合点之间反复传播导致的结果。中期阶段拦阻力的仿真结果与试验数据存在一定的差别，但拦阻过程中拦阻力变化的形式一致，中后期拦阻力趋于平稳的趋势一致，总体而言仿真结果具有良好的一致性与可信度。

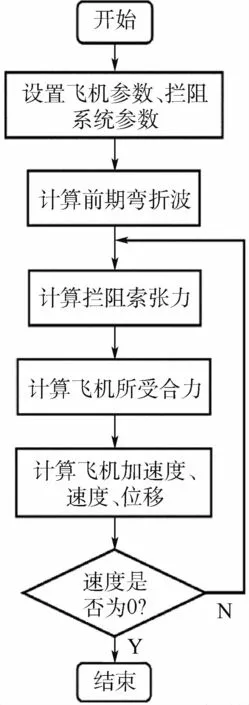
图7 模型求解流程图Fig.7 Flowchart of model calculation

表1 舰载飞机及拦阻装置参数［22］Table 1 Parameters of carrier-based aircraft and arresting gear［22］

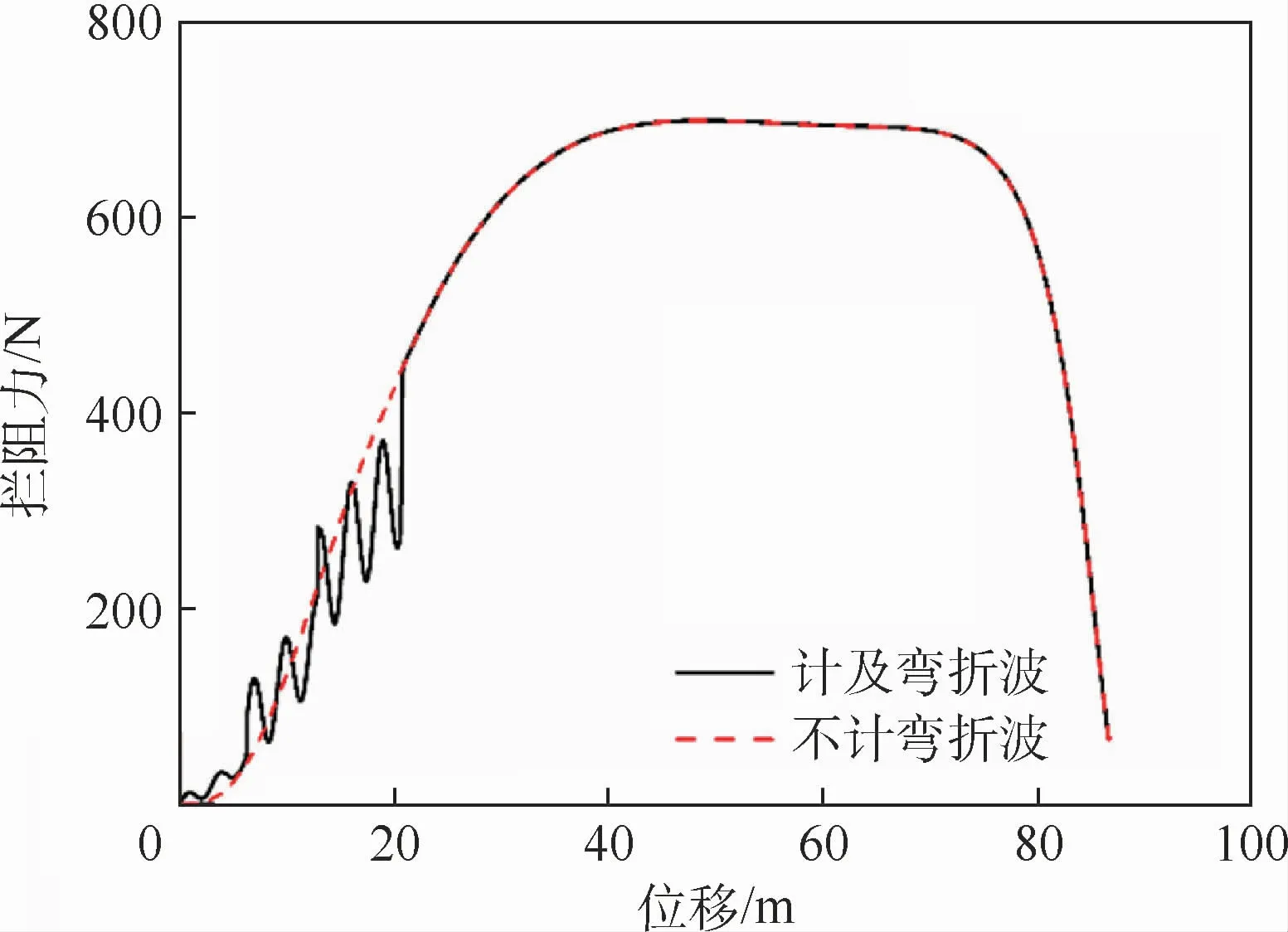
图8 对中拦阻时拦阻力-位移曲线Fig.8 Arresting force-displacement curve in centering arrest

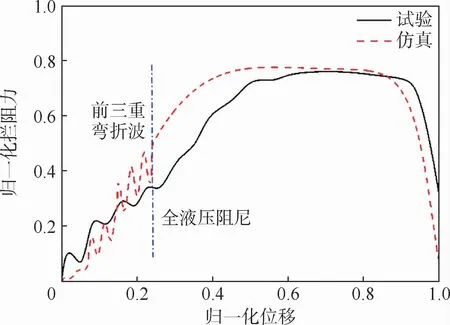
图9 仿真与试验拦阻力-位移曲线对比Fig.9 Comparison of arresting force-displacement curve between simulation and test

4 计算与分析

在模型中设置偏心度，进行偏心拦阻动力学仿真，所有算例偏心时均为右偏，其他参数与对中拦阻仿真时一致。

4.1 偏心度对弯折波的影响

在右偏心拦阻时，右侧前三重弯折波先结束，之后左侧三重弯折波才结束。分析偏心度对前三重弯折波期间两侧带拉力影响，结果如图10所示。

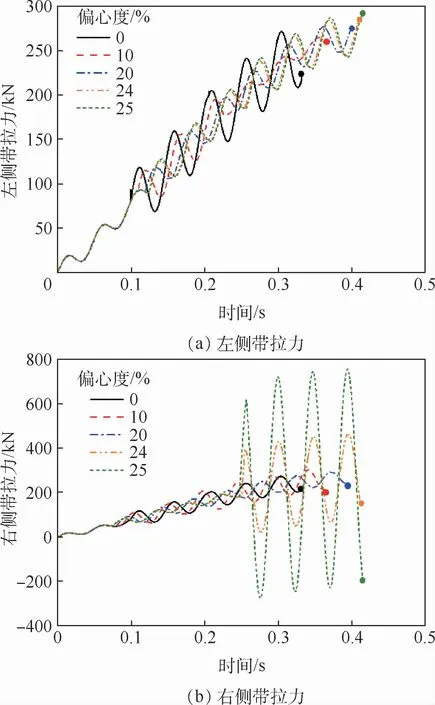
图10 弯折波期间左右侧带拉力Fig.10 Port tape and starboard tape tension during kink-wave period

将不同偏心度时两侧前三重弯折波的时长结果列入表2进行比较分析。

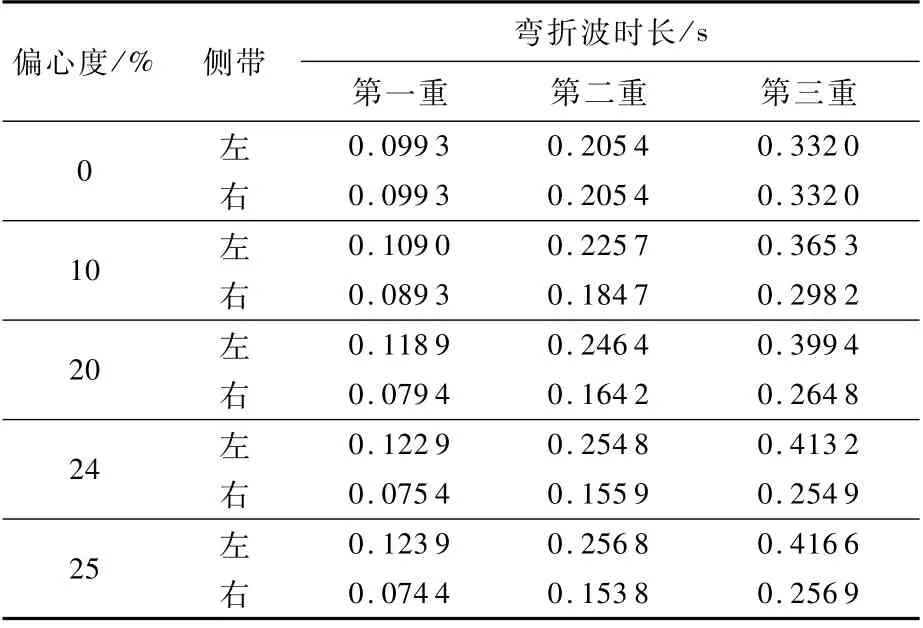
表2 弯折波时长对比Table 2 Comparison of duration of kink-wave

从结果明显看出，在右偏心拦阻时，左侧弯折波随着偏心度的增加时长增加，右侧弯折波随着偏心度的增加时长减小。原因是右偏心拦阻时右侧拦阻索初始长度短，弯折波传播的时间短，拦阻索拉出速度变快，导致载荷波动幅度以及波动频率变大。

由图10（b）可知，当偏心度大于20%时，偏心侧前三重弯折波波动变得十分剧烈，载荷不再呈现整体波动上升的趋势，根据文献［7］中内容，实际拦阻接受的偏心距不超过舰上拦阻索长度一半的20%，本文结果与该结论一致。

当偏心度为24%时，弯折波造成的拦阻带拉力波动已十分剧烈，但仍处于正拉力状态。在本文建立的模型基础上，一旦偏心度达到25%，偏心一侧拦阻带拉力会出现负值，此时偏心侧拦阻索处于松弛状态，极有可能造成拦阻索脱钩，最大带拉力接近拦阻索破断拉力784 kN，这都会导致拦阻失败。

4.2 偏心度对单侧带拉力的影响

分析偏心度为0%、10%、20%、24%时单侧带拉力的变化趋势，结果如图11所示。

将不同偏心度下左侧最大带拉力和右侧最大带拉力的结果列入表3进行比较分析。

由表3结果可以看出，在右偏心拦阻时，随着偏心度的增加，右侧拦阻系统的带拉力相比对中拦阻时逐渐增大，偏心度为24%时右侧最大带拉力为481.79 kN；左侧拦阻系统的带拉力相比对中拦阻时逐渐减小，偏心度为24%时左侧最大带拉力为328.53 kN。

4.3 偏心度对两侧带拉力的影响

分析偏心度为0%、10%、20%、24%时两侧拦阻带拉力的对比变化趋势，结果如图12所示。

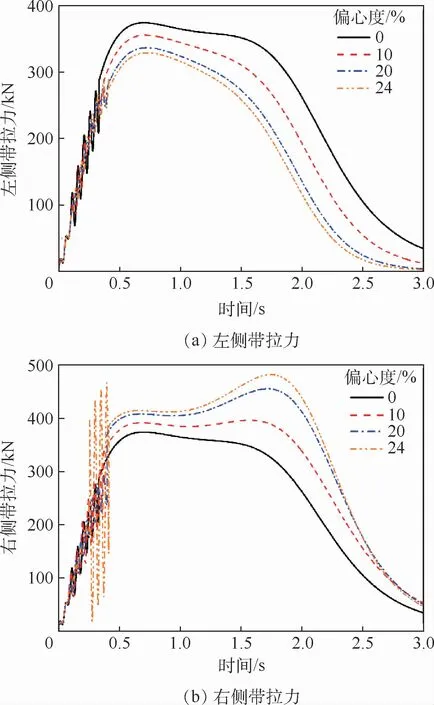
图11 偏心拦阻左右侧带拉力Fig.11 Port tape and starboard tape tension in off-center arrest

表3 不同偏心度左右侧最大带拉力对比Table 3 Comparison of maximum port and starboard tape tension under different eccentricity

由图12可以看出，随着偏心度的增加，两侧带拉力相差越大，偏心侧带拉力比背离侧带拉力大。偏心拦阻相比对中拦阻，因左右两侧拦阻索伸长量不同，使得两侧活塞的速度不同，使得两侧拦阻带拉力不同。

当偏心度变大时，两侧拦阻索上载荷相差越大，使得偏心侧的拦阻索承受更多的拦阻冲击载荷，可能会使偏心侧拦阻索承受应力过大导致断裂，甚至会导致拦阻钩发生塑性变形，导致最终拦阻失败。

4.4 偏心度对拦阻系统性能的影响

分析偏心度为0%、10%、20%、24%时飞机位移、速度、航向加速度以及所受拦阻力的响应，结果如图13所示。

图12 偏心拦阻左右侧带拉力对比Fig.12 Comparison of port and starboard tape tension in off-center arrest

将不同偏心度下拦阻系统和飞机响应的计算结果列入表4进行比较分析。

图13 不同偏心度飞机响应Fig.13 Aircraft response with different eccentricity

从表4的对比结果可以看出，偏心拦阻相比对中拦阻，随着偏心度的增加，拦阻力峰值略有减小，但偏心度过大时在拦阻后期拦阻力峰值变大。偏心度对拦阻位移、飞机航向加速度峰值影响较小。该结果与文献［23］中偏心拦阻对钩载的影响的试验结果所得到的分析结论是一致的。

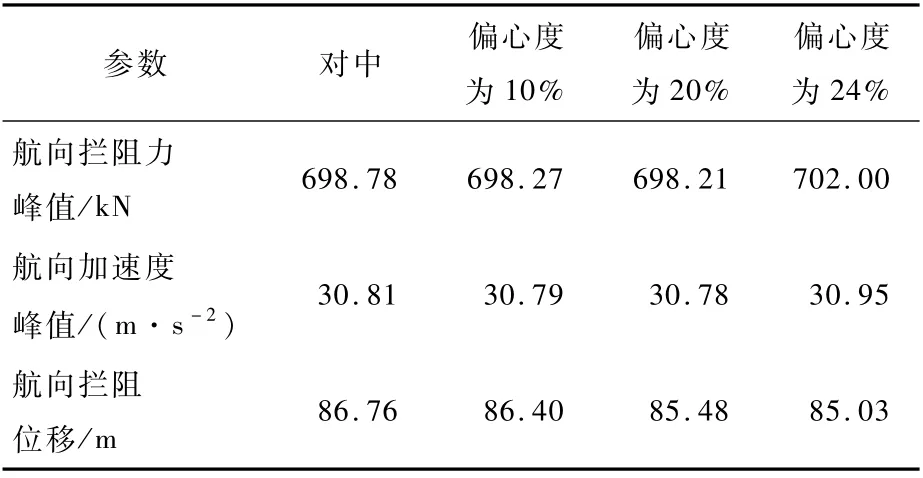
表4 不同偏心度仿真结果对比Table 4 Comparison of simulation results under different eccentricity

5 结 论

针对舰载飞机着舰时可能出现的非对称拦阻问题，建立了完整的拦阻系统动力学模型，用美军标的试验结果验证了模型的准确性，进行不同工况下的偏心拦阻动力学仿真，通过对仿真结果的综合分析表明：

1）偏心拦阻时，随着偏心程度的增加，偏心侧前三重弯折波时长变短，背离侧弯折波时长变长。且偏心程度较大时，偏心侧弯折波波动变得剧烈。一般要求偏心度小于 20%，不得超过24%。

2）偏心拦阻时，偏心侧拦阻带拉力比对中时的大，背离侧拦阻带拉力比对中时的小。且随着偏心程度的增加，偏心侧拦阻带拉力最大值变大。

3）偏心拦阻时，偏心侧拦阻带拉力的峰值比背离侧的大，且随着偏心度的增加，两侧拦阻带拉力峰值的差距越来越大。偏心侧拦阻索分担更多的拦阻冲击载荷，这对于纠偏存在不利影响。偏心度过大时，偏心侧拦阻带拉力峰值可能会超过拦阻索许用拉力，造成拦阻失败。

4）偏心拦阻对拦阻距离、飞机减速过程、拦阻力峰值、航向加速度峰值影响较小。随着偏心度增加，拦阻距离和拦阻力峰值稍有减小，但偏心度过大时，在拦阻后期拦阻力峰值又会变大。