解三角形中的取值范围问题探究

北京市第十二中学高中部(100071) 刘 刚

翻阅近些年的各类考题,发现解三角形中的取值范围问题比比皆是,解决这类问题通常要借助三角函数的有界性、均值不等式、导数等知识处理,有时也可以构造图形,从几何直观角度理解与认识.下面结合一道具体题目,谈一谈这些方法的应用.

题目已知锐角ΔABC中,a=1,A=求b2+c2的取值范围.

思路1借助正弦定理,把b2+c2转化为三角函数,然后分析角的取值范围,最后借助三角函数的有界性解决.

解法1由正弦定理,得所以于是

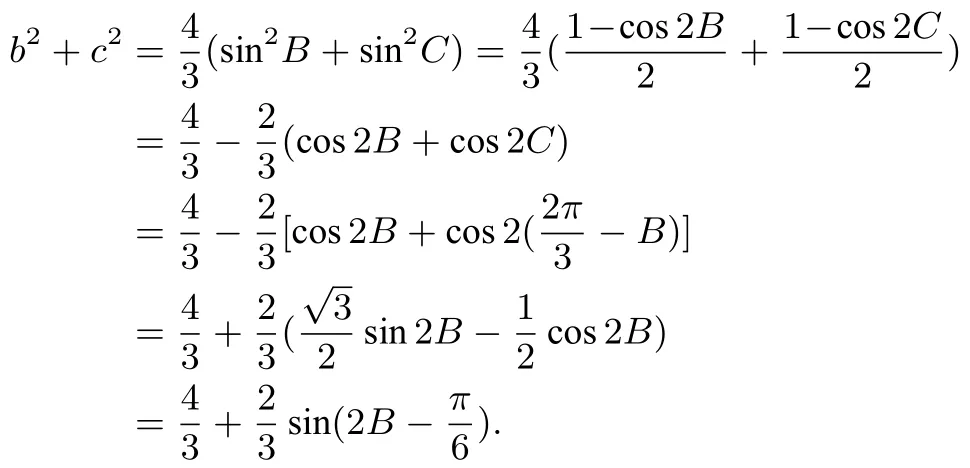
因为ΔABC为锐角三角形,所以即由此得＜sin(2B-)≤1,于是＜b2+c2≤2,故b2+c2的取值范围是(,2].

点评以上化简与变形要熟练掌握三角公式,同时转化的目标要明确:把所求代数式化为Asin(ωx+φ)+k,其中ω＞0(或Acos(ωx+φ)+k,其中ω＞0)的形式,这样便于借助三角函数的有界性解决范围问题.同时,本题要特别注意角度B的取值范围,有不少同学不加思考,认为由锐角三角形可得0＜B＜这是片面的,还应该考虑这样才能得到B的准确范围.

变式1已知a=(2 cosx,2 sinx),b=(sin(x-),cos(x-)),函数f(x)=cos〈a,b〉.

(1)求函数f(x)的零点;

(2)若锐角ΔABC的三个内角A,B,C的对边分别是a,b,c,且f(A)=1,求的取值范围.

解(1) 略.(2) 由已知可得f(x)=sin(2x-),所以f(A)=sin(2A-)=1,解得2A-=2kπ+,即A=kπ+k ∈Z.又0＜A＜π,所以A=由正弦定理,得

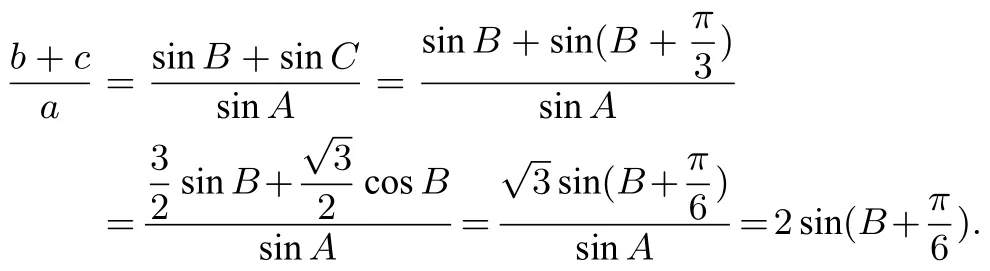
因为ΔABC为锐角三角形,所以即由此得＜sin(B+)≤1,即≤2,故的取值范围是

思路2设=t,先借助余弦定理把b2+c2转化为关于t的函数,然后找出t的取值范围,最后借助导数解决.

解法2因为a=1,A=所以由余弦定理,得

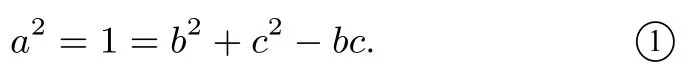
因为ΔABC是锐角三角形,所以即将①代入,解得设则t ∈由①,得c2=所以b2+c2=

设f(t)=则f′(t)=于是当t ∈时,f′(t)＞0,f(t)单调递增;当t ∈(1,2)时,f′(t)＜0,f(t)单调递减,所以当t=1 时,f(t)有最大值为2.又所以＜f(t)≤2,即＜b2+c2≤2,故b2+c2的取值范围是

点评由于所求代数式b2+c2有两个未知量,因此需借助余弦定理、换元等方式转化为一个未知量,接下来构造函数并借助导数研究,体现了函数与方程的思想.

变式2(2019年高考全国Ⅲ卷理科第18 题) ΔABC的内角A,B,C的对边分别为a,b,c,已知asin=bsinA.

(1)求B;

(2)若ΔABC为锐角三角形,且c=1,求ΔABC面积的取值范围.

解(1)略,B=;(2)因为c=1,B=,所以由余弦定理,得

因为ΔABC为锐角三角形,所以即将②代入,解得＜a＜2.因为ΔABC的面积SΔABC=所以＜SΔABC＜故ΔABC面积的取值范围是

思路3借助正(余)弦定理、均值不等式、三角函数的性质求解.

解法3因为a=1,A=所以由余弦定理,得a2=1=b2+c2-bc≥b2+c2-解得b2+c2≤2,当且仅当b=c时等号成立.因为B是锐角,所以b2=c2+1-2ccosB＜c2+1,即c2＞b2-1,于是b2+c2＞2b2-1 恒成立.由正弦定理,得所以b=于是b2+c2＞因为ΔABC为锐角三角形,所以由此得故b2+c2的取值范围是

点评解法3 首先借助余弦定理以及均值不等式b2+c2≥2bc得到了b2+c2≤2.怎样求b2+c2的下确界呢? 先通过放缩得到不等式b2+c2＞2b2-1 恒成立,接下来借助正弦定理得到b=sinB,最后根据三角函数的性质求解,体现了转化思想.

变式3在ΔABC中,B=,b=1,D为边AC的中点,求BD的取值范围.

解由已知得BD是ΔABC的中线,所以(2BD)2+AC2=2(BA2+BC2),把b=1 代入,得

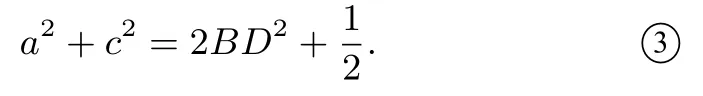
因为B=,b=1,所以由余弦定理,得a2+c2-ac=1,于是a2+c2=ac+1≤+1,解得a2+c2≤2,代入③,解得BD≤当且仅当a=c时等号成立.因为ac＞0,所以a2+c2=ac+1＞1,代入③,解得BD＞

思路4根据a=1,A=所以可得点A在一段圆弧上运动,由此借助图形求解.

解法4如图1,作ΔABC的外接圆O,因为a=1,A=且ΔABC是锐角三角形,所以点A在劣弧上运动(不包括端点).

由余弦定理,得b2+c2=bc+1,且bc=过点O作BC的垂线交劣弧于点A0,交BC于点D,则D为BC的中点,所以A0D就是点A到BC距离的最大值,此时ΔABC为等边三角形,求得ΔABC面积的最大值为又当点A在A1或A2处时,ΔABC的面积为于是即＜bc≤1,由此得＜b2+c2≤2,故b2+c2的取值范围是

点评由于b2+c2的几何意义不易直接体现,所以联想余弦定理、三角形面积公式进行转化,即b2+c2=bc+1,且接下来只需研究ΔABC面积的取值范围即可,解法体现了直观性与问题的本质.

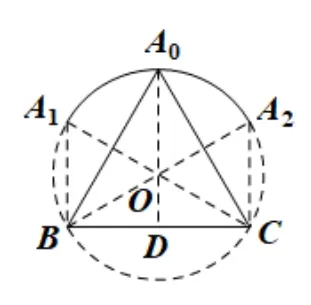
图1

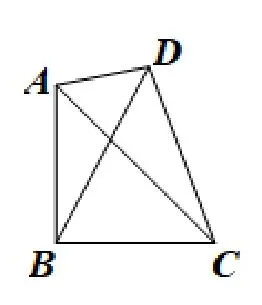
图2

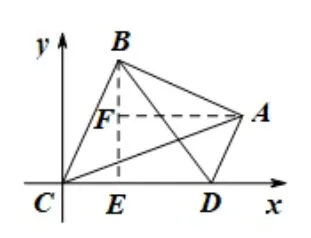
图3

变式4如图2,已知ΔABC是以AC为斜边的等腰直角三角形,D为ΔABC外的一点,且CD=2AD=2,则ΔBCD面积的最大值为____.

解如图3,以C为原点,CD所在直线为x轴建立平面直角坐标系,则D(2,0).过点B作x轴的垂线,垂足为E,过点A作BE的垂线,垂足为F,由已知可得ΔBCE∽=ΔABF,所以CE=BF,BE=AF.

设B(x,y),则点A的坐标为(x+y,y-x).因为AD=1,所以(x+y-2)2+(y-x)2=1,化简,得(x-1)2+(y-1)2=故点B的轨迹是以点(1,1) 为圆心,半径为的圆.因为SΔBCD=且|yB|≤+1,所以SΔBCD≤+1,当点B的坐标为(1,+1)时等号成立,所以ΔBCD面积的最大值为

以上借助三角函数的有界性、导数、均值不等式、几何图形等方法解决了一道三角形中的取值范围问题,这些方法均是常用方法.在解决三角形中的取值范围问题时,由于方法多,所以不能局限于某一种解法,应鼓励学生从不同角度探索,培养学生的发散性思维.只有这样,才会串联起所学知识,形成知识网络,进而落实“四基”与“四能”,数学核心素养的提升也就指日可待了.