基于异或的外形比例不失真(k,n)视觉密码方案
2020-09-09张皓宇季姝廷
董 晨 张皓宇 季姝廷 李 磊
1(天津理工大学计算机科学与工程学院天津市智能计算及软件新技术重点实验室 天津 300384)2(天津市大数据管理中心 天津 300221)
0 引 言
作为一种秘密共享技术,视觉密码[1](Visual Cryptography,VC)具有理论安全和恢复简单的特点。它将秘密分享为若干杂乱无章的共享份,恢复时将足够数量的共享份叠加,自提出以来,便引起众多学者的重视和研究兴趣[2-4]。
在视觉密码的早期研究中,方案主要采用透明胶片为介质,因而其恢复操作只能是叠加,亦即布尔二元运算中的“或”运算。无论是Naor等[1]最早给出视觉密码的(n,n)方案,还是Droste等[5]通过设计加密矩阵给出相对差为1/m(m为加密矩阵列数)的(k,n)方案,都存在像素扩展度较大、外形比例失真和相对差较小的问题,需要进一步对视觉密码方案参数进行优化。为此,Hou等[6]提出了一种多点加密技术,对秘密图像逐行进行扫描,每分享m个黑(白)像素就使用了加密矩阵的所有列,实现了秘密图像的不扩展分享与恢复,虽然恢复图像的外形比例不失真,但该方案的相对差没有得到实质性提高。
另一种实现像素不扩展的方法是随机栅格法,文献[7]设计了基于随机栅格(Random Grid,RG)的视觉密码(RG-based VC,RGVC),共享份是与原始图像尺寸相同的光栅,通过将共享份进行“或”叠加,通过黑白区域的光通量不同来显现秘密信息。由于RGVC只借助随机函数来实现秘密共享[8],因此共享过程不依赖加密矩阵是RGVC的优势,可以有效减小加密矩阵的存储开销。依据该思路,Shyu[9]基于二元运算的3种函数fequ、fran和fcom设计了一种(2,2)方案的秘密分享算法。此后,Chen等[10]、Guo等[11]和Hu等[12]相继设计了存取结构为(2,n)、(n,n)和(k,n)的RGVC改进方案。Shen等[13]分析了RGVC方案到加密矩阵方案的变换,指出随机栅格是加密矩阵的算法表示。事实上,RGVC方案是加密矩阵方案的一个特例,同样存在恢复效果不佳的问题,因此设计更优的加密矩阵方案成为当前主流的研究思路。
综上所述,尽管现有方案在像素扩展度方面得到了优化,但始终存在恢复图像相对差低的问题。本质上,该类方案用“或”运算执行像素叠加,从代数结构上讲,其操作都属于半群结构,使得像素无法实现完全恢复,特别地,对于表示白像素的0而言,其代数结构不存在逆元,是限制恢复效果进一步改善的根本原因。为了突破基于透明胶片叠加的运算介质对方案的影响,Biham等[14]提出了基于偏振光的视觉密码,恢复像素的颜色不再是共享份对应像素“或”运算的结果,而是由共享份偏振方向的平行“或”正交来决定,该操作可以表示为“异或”(XOR)运算,具有像素扩展度小和相对差大的特点,但方案依赖特定的光学设备,恢复过程较为复杂。随着现代科学技术的发展,具有计算能力的智能终端在现实应用中日益普及,为实现“异或”操作提供了简便途径,Tuyls等[15]首次给出基于XOR视觉密码的定义,并实现了(n,n)方案的完全恢复,但该方案的分享算法不适用于一般的(k,n)存取结构。郁滨等[16]结合(n,n)“异或”方案的加密矩阵,提出了共享份分块构造的设计思路,可以实现相对差的无失真恢复,但叠加图像的外形比例存在失真。
针对以上问题,本文设计基于奇偶列的加密矩阵构造方法,在图像分享时,通过改进多行扫描、多点加密技术,构造出一种基于“异或”的(k,n)秘密分享算法,在实现恢复图像外形比例不失真的前提下,提高了相对差,最后,通过理论和实验验证方案安全性和对比性。
1 基本概念
设共享集合为K={i1,i2,…,in},定义授权集合为Q(Q⊆K且|Q|≥k),禁止集合为P(P⊆K且|P| 定义1称两个n×m布尔矩阵为元素的集合C0和C1构成一个(k,n)“异或”视觉密码方案,其中C0表示分享白像素的映射空间,C1表示分享黑像素的映射空间,在分享白(黑)像素时从C0(C1)中随机选取一个矩阵S0(S1),对应n个共享份各自的m个子像素,则矩阵S0、S1满足下列两个条件: 1) 安全性条件:当X⊆P时,H(V(X,S0,⊕))=H(V(X,S1,⊕))。 2) 对比性条件:当X⊆Q时,H(V(X,S1,⊕))-H(V(X,S0,⊕))>0。 安全性条件表明当参与者人数小于k时,禁止集合P中的参与者无法获得秘密图像的任何信息。对比性条件表明当参与者人数等于k时,授权集合Q中的参与者通过共享份“异或”运算可以实现秘密恢复。评价视觉密码方案有两个重要参数:像素扩展度m和相对差α。 定义2设(k,n)-VCS加密矩阵为S0和S1,任取S0(或S1)中k行,当S0中此k行的任意列向量l中含有奇数个“1”(或S1中k行的任意列向量l′中含有偶数个“1”)时,则称向量l(l′)为矩阵S0(或S1)的多余列。将l(l′)的k行中所含有“1”的个数记为r。 关于上述定义的三点补充说明: 1)m表示原始图像中的一个像素在分享图像中扩大的子像素的个数,也就是原始图像经过扩展后在面积上失真的倍数。像素扩展度越大所需的存储空间就越大,即代表其在面积上的失真也会越大。 2)α是恢复图像中代表黑像素的向量汉明重量最小值l与代表白像素的向量汉明重量最大值h之差与像素扩展度m之比,即:α=(l-h)/m,其中α∈[0,1],当α=0时代表黑白像素的灰度值相等,完全不能辨别出原图像,即无法识别秘密信息;当α=1时代表恢复图像中黑白像素完美恢复,是最理想的情况。 3) 定义2给出多余列的概念,用于后续算法2中加密矩阵的构成。 本节构造一种外形比例不失真的(k,n)“异或”视觉密码方案的秘密分享和恢复流程,并对方案的有效性进行证明。 为进一步优化视觉密码相关参数,本文通过添加奇偶列的方法构造加密矩阵,通过融合多行扫描和多点加密技术,构造(k,n)方案的秘密图像分享流程如图1所示,通过该流程生成的共享份不存在像素扩展。 算法1秘密图像分享算法 输入:秘密图像S。 输出:共享份SI1,SI2,…,SIn。 Step1读取原始秘密图像S中的各像素信息。 Step3计算这m个像素中黑像素的个数,记为b,用eb代表已经完成扫描的像素中含有b个黑像素的扫描序列的个数,其中b=(0,1,…,m),初始时定义eb=0。 Step5将这m个像素按扫描顺序依次标记为向量Plj=(Vl1,Vl2,…,Vlm),(l=1,2,…,m),用l标记完成扫描序列的个数,j表示当前扫描到的像素在Plj标记向量中的位置,初始化l=1,j=1。 Step7判断是否j=m。若是,则返回Step 2,重新扫描;若不是,则令j=j+1,进行下一个像素的处理。 Step9输出生成的共享份SI1,SI2,…,SIn,算法结束。 关于算法1的三点补充说明: 1) Step 2-Step 4实现秘密图像的多行扫描,按行列顺序依次将秘密图像以m个像素为单位进行划分,并计算各m个像素中黑像素个数; 3) Step 4中加密矩阵设计是算法的核心环节,本文提出一种基于奇偶列的加密矩阵构造方法,具体如算法2所示。 加密矩阵的构造流程如图2所示。 图2 加密矩阵构造流程 算法2加密矩阵构造算法 输入:门限结构(k,n),n≥k≥2。 输出:加密矩阵(C0,C1)。 Step1对于所有偶数p(0≤p≤k),若2p≤k,则令q=p;否则,令q=n+p-k,将所有含q个“1”的n维列向量的组合添加到矩阵C0中。 Step2对于所有奇数p(0≤p≤k),若2p≤k,则令q=p;否则,令q=n+p-k,将所有含q个“1”的n维列向量的组合添加到矩阵C1中。 Step3依据定义2,在C0和C1中添加多余列:1) 将C1中的多余列用Step 1和Step 2的方法添加到C0中,生成新的C0;2) 将C0中的多余列添加到C1中,生成新的C1。 Step4判断C0、C1中的多余列是否相等,若相等,则该步骤结束,否则转到Step 1。 Step5生成和输出加密矩阵C0、C1,算法结束。 秘密恢复如图3所示,依据(k,n)门限原理,从生成的n个共享份SIi(i=1,2,…,n)中任取k个,采用“异或”操作进行叠加,即可恢复出原秘密图像。 图3 秘密恢复流程 依据定义1,本节分别从安全性和对比性两个方面对方案的有效性进行形式化证明。 引理1[1]:在(k,k)-VCS中,加密矩阵C0(k×k)中任意一列1的个数为偶数,C1(k×k)中任意一列1的个数为奇数。 定理2(安全性) 当X⊆P时,H(V(X,C0,⊕))=H(V(X,C1,⊕))。 证明:根据(k,n)方案的加密矩阵构造方法,C0(C1)中任取k行产生的多余列将以同样数目添加到C1(C0)中去,将C0(C1)中任取k行产生的所有多余列和从C1(C0)添加过来的所有多余列合并在一起生成加密矩阵C0(C1)的相同列,通过添加多余列来保证加密矩阵C0(C1)的任意k行由引理1中的矩阵C0(k×k)(C1(k×k))相同列构成。故C0、C1任意k行中相同列所包含的列向量相同,由于相同列具有相同的汉明重量,在只考虑任意k行时可以忽略。对于C0(C1)取k行剩余的偶数(奇数)列,满足C0(k×k)(C1(k×k))矩阵的特性。任取p(p 则在指定扩展位置,对于奇数列p有SUM1或SUM2种将C0(p×p)(C1(p×p))扩展为基本C0(k×k)(C1(k×k))矩阵的组合方式,利用组合数学可以证明SUM1=SUM2[5],此处不再赘述。 同样反过来,可以推导出C0、C1中任意p(p 定理3(对比性) 当X⊆Q时,H(V(X,S1,⊕))-H(V(X,S0,⊕))>0。 证明:如果X⊆Q,则存在参与者个数大于等于门限值k。当参与者个数等于k时,(C0,C1)中任意k行包含(C0(k×k),C1(k×k))及相同列,由于相同列无论是“异或”还是“或”叠加所得到的汉明重量相等,不影响汉明重量差。则对于C0(k×k)(C1(k×k))中的偶数(奇数)列,H(V(X,C1(k×k),⊕))-H(V(X,C0(k×k),⊕))=2k-1>0,即参与者个数为k时秘密图像可恢复。当参与者个数大于k时,任取其中k个共享份“异或”叠加即可恢复图像,满足定义1中的对比性条件。 下面以图4黑白秘密图像S为例,采用(4,5)门限结构对方案有效性进行实验验证。首先利用2.1节算法2构造(4,5)方案的加密矩阵如下: (a) 秘密图像S(b) 共享份SI1 (e) 共享份SI4(f) 共享份SI5图4 秘密图像与共享份 利用2.1节算法1生成共享份SI1、SI2、SI3、SI4、SI5,如图4所示,基于2.2节恢复流程得到叠加图像如图5所示,依据第1节相对差计算公式得到方案参数如表1所示。可以看出,共享份图像完全杂乱无章,不会泄露原秘密图像S的任何信息,当少于4个共享份进行叠加时,也无法恢复秘密信息,验证方案的安全性。当不少于4个共享份进行“异或”运算时,可以显示秘密信息,验证方案的对比性,即必须满足(k,n)门限条件时才可完成秘密恢复。 (a) SI1⊕SI2(b) SI2⊕SI3⊕SI4 (c) SI1⊕SI2⊕SI3⊕SI4(d) SI1⊕SI2⊕SI3⊕SI4⊕SI5图5 不同数量共享份叠加效果 表1 方案参数比较 将本文与文献[12,16]进行对比,恢复效果比较如图6所示。可以看出,文献[12]的恢复图像虽然不存在像素扩展但恢复效果不佳,由于文献[12]设计受限于“或”运算,导致恢复图像的相对差为1/8,而本文中4个共享份进行恢复时的相对差为8/15,恢复效果明显优于文献[12];文献[16]基于“异或”运算设计,虽然能实现秘密区域的完美恢复,但恢复图像较原始图像S在外形尺寸上存在较大失真,像素扩展为2.5,特别地,当k、n值逐渐增大时,像素扩展度m迅速增加,不便于共享份图像的传输和存储。综上,本文方案在实现外形比例不失真的前提下,明显提高相对差,折中考虑像素扩展度和相对差,使方案关键参数得到优化。 (a) 本文恢复效果(b) 文献[12]恢复效果 本文提出的(k,n)“异或”视觉密码方案,通过添加奇偶列的方法构造加密矩阵,在秘密分享时利用多行扫描、多点加密逐像素点进行加密,恢复图像实现外形比例不失真,且增大相对差,优化共享份图像的存储和传输开销,并改善秘密图像的恢复效果。但本文方法无法实现秘密图像的完美恢复,与原始图像相比,恢复图像相对差仍存在一定的失真,如何进一步优化是后续研究重点。2 方案设计
2.1 秘密分享流程






2.2 秘密恢复流程

3 方案有效性证明
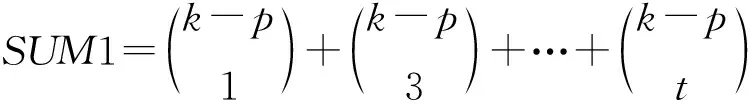

4 实验分析






5 结 语
