IABC-elite算法在电液比例溢流阀压力控制中的应用

方锡岗， 周孟然， 胡锋， 周悦尘， 余道洋

（1.安庆联动属具股份有限公司，安徽 安庆246001；2.安徽理工大学，安徽 淮南232000）

0 引 言

压力控制是液压技术中一个不可或缺的重要部分，溢流阀是一种常用的液压压力控制阀。但普通溢流阀大多通过调压螺钉手动整定，存在压力转换不平稳、压力控制精度不高、压力响应滞后等缺陷。电液比例溢流阀采用比例电磁铁作为控制阀芯，相比手动控制的弹簧组件，可以做到无级调压，通过控制器的压力闭环控制，可以使输入压力快速响应，平稳转换，大大提高工作效率。

在工业控制现场中，PID控制器的应用十分广泛，具有算法简单、可靠性高、鲁棒性好等特点，但是对于一些非线性、大惯性、大延迟系统，控制效果不尽人意，难以满足控制要求。所以出现了很多寻优算法被用来优化PID控制器的例子，如傅晓云等[1]利用粒子群优化PID参数；赵亚琪等[2]采用遗传算法优化PID参数。大部分智能优化算法都能轻松胜任PID参数寻优，但也存在收敛速度较慢、易陷入局部最小等缺陷。

标准人工蜂群算法(SABC)由土耳其学者Karaboga[3]于2005年提出，是一种新型的模拟蜂群社会行为的仿生算法，相比于其他群算法，SABC在收敛速度和全局性上表现更好，但也存在早熟收敛、局部搜索能力弱及在搜索后期收敛速度慢等缺陷。

ZHU等[4]在2010年提出了基于全局最优解gbest的GABC算法，首次将gbest引入ABC算法，加快了算法的收敛速度，但其基于当前最优的优化策略可能会使算法陷入“早熟”；卢滢宇[5]在2012年提出了基于局部最优解的ABC算法，可动态调整领域搜索频率，提高了算法局部搜索和全局搜索的平衡性，但是其邻域搜索公式较为复杂，尚有可以改进的空间；李彦苍等[6]在2015年提出基于信息熵的改进ABC，提高了搜索效率，并应用于TSP问题的求解，优化效果良好，但是终止算法的熵值始终没有统一标准，存在一定的随意性。2016年，文献[7]提出了基于精英解的人工蜂群算法(ABC-elite)，结合精英解和gbest在加速收敛和避免“早熟”之间取得了较好的平衡，本文改进了ABC-elite，动态调整了精英解和gbest的权重，对雇佣蜂的更新公式作出调整，得到IABC-elite算法并应用于电液比例溢流阀的PID参数寻优。

1 电液比例溢流阀压力控制系统

电液比例溢流阀压力控制的系统框图如图1所示。

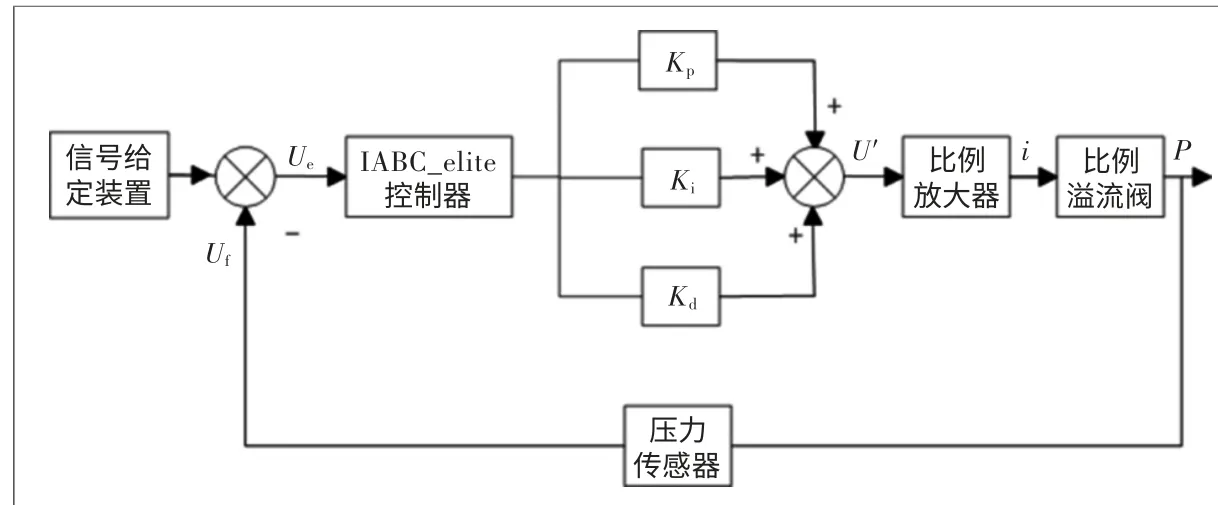
图1 电液比例溢流阀压力控制系统框图

其工作过程为：压力传感器检测出比例溢流阀出油口压力，反馈的压力值与设定值之差输入IABC-elite控制器。其中，由于PID控制器的比例、积分、微分环节受Kp、Ki、Kd这3个参数的影响很大，在这里将PID部分直接化简为3个参数，由IABC-elite控制器对这3个参数寻优，得到的PWM电压信号经过比例放大后输入比例溢流阀。

关于比例放大器的数学模型，由于比例放大器与整个系统的固有频率相比，响应特性较高，所以可化简为比例环节：

式中：Ka为比例放大器的增益；I(s)和U(s)分别为比例放大器的输出电流和输入电压。

许多学者对比例溢流阀模型都进行了深入的分析和描述[8-10]，但得到的数学模型十分复杂，不利于仿真和实验分析。本文将对电液比例溢流阀模型向二阶系统简化。由于系统为非最小相位系统，忽略对系统影响较小因素及干扰，比例溢流阀传递函数可以表示为

式中：ω0为阀的综合固有频率；ξ0为阀的综合阻尼比。

所以，确定电液比例溢流阀传递函数的实质就是确定ω0、ξ0这两个参数的值。根据文献[9]的bode图分析结果，可以初步判定0.7<ξ0<1.0，25 rad/s<ω0<40 rad/s。经过多次的实验试凑，ξ0和ω0分别取0.95和36 rad/s为最佳。将参数代入式(2)中得

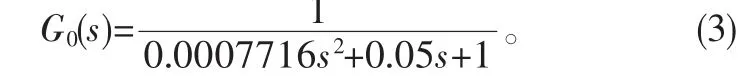
2 标准人工蜂群算法

在SABC中，蜂群包含3种不同分工的蜜蜂：雇佣蜂(employed bees)、跟随蜂(onlookers)和侦查蜂(scouts)。

雇佣蜂发现食物源并记录食物源信息；跟随蜂根据雇佣蜂携带的食物源信息选择是否跟随；当一个食物源被放弃时，雇佣蜂转变为侦查蜂，随机寻找下一个食物源。

在算法中，食物源被定义为一个拥有D维属性的可行解，解的个数等于雇佣蜂数，解的质量用适应度函数定义。初始解根据公式(4)产生：

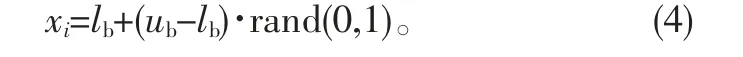
式中：ub和lb分别为解元素的上界和下界；rand(0,1)为(0,1)上的随机数。

随后，雇佣蜂开始对种群进行循环搜索，在每一个初始解的邻域内都将搜索出一个随机解，跟随蜂会根据食物源的信息按照一定的概率进行选择。跟随蜂重复上述操作。

跟随蜂和侦查蜂根据公式(5)进行搜索：

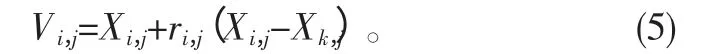
式中：Xi，j为第i个解的第j维；Xk，j为第k个解的第j维，且k≠i；ri，j为[-1,1]上的随机数。

解被跟随蜂选择的概率，根据公式(6)确定：

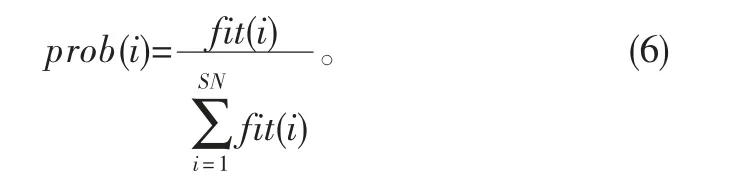
式中：prob(i)为第i个解被选择的概率; fit(i)为第i个解的适应度。

如果某个解经过limit次迭代后仍未被改善，则可以判定这个解已经陷入局部最小，被雇佣蜂舍弃，此时雇佣蜂转变成侦查蜂并根据式(7)寻找新解：

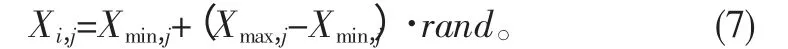
式中：Xmin，j为到当前代第j维最小值；同理，Xmax，j为最大值;rand为[-1,1]上的随机数。

3 本文提出的算法

3.1 优化思路

众所周知，对于基于群的启发式算法例如ABC、PSO、GA、DE(差分进化算法)等来说，探索和开发是两个非常重要的迭代过程。探索指的是算法在解空间中，调查未探索过的区域从而找出全局最优解的能力；开发指的是运用当前最优解，发现更优解的能力。但是两者互相矛盾，如果想拥有较强的探索能力（即在全局范围内搜索，不容易陷入局部最小），则必须舍弃部分收敛速度。反之，如果想拥有较快的收敛速度，则陷入局部最小的风险会增大。所以，如何较好地平衡两者，是优化算法的关键所在。

ZHU等[4]在PSO的启发下，于2010年提出了基于当前全局最优解gbest的ABC，雇佣蜂和跟随蜂的更新公式为

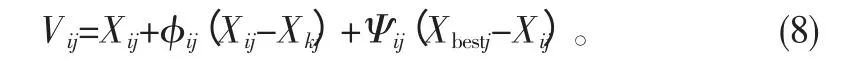
其中：等号右边前两项与SABC相同；第三项中Ψi，j为[0,c]之间的随机数，经过仿真试验后得到c取1.5为最优；Xbest，j为gbest。

我们暂且可以定义等式右边第一项为搜索基项，后两项分别为随机引导项和gbest引导项。但等式后两项如果互为相反数，则相互抵消并呈现收敛振荡，所以GAO等[11]对搜索公式做出改进，采用一个基项加一个引导项的模式，搜索公式如下：

ABC-elite相比于前两种算法的优势在于采用一个引导项与一个基项的和的形式，避免了收敛振荡，但这种公式形式很难兼顾探索和开发，所以在雇佣蜂和跟随蜂阶段采用不同的搜索公式加以专精。但是，对于式(10)中以精英解为引导项的方法并不能提高算法的全局性。更重要的是，式(11)中，以gbest和精英解的均值作为基项，相当于将两者对算法的影响等同看待，这样做既没有充分利用种群中最成功个体的经验，也不利于算法的快速收敛。

3.2 改进精英人工蜂群算法

寻优算法在整个迭代过程中对于探索和开发能力的着重是不同的，在迭代前期，希望算法能够迅速开发、尽快收敛，而到了迭代后期又希望尽量在整个解空间进行探索，避免陷入早熟。对于ABC-elite算法，本文引入了一个参数μ，可以随着迭代次数的增加动态改变精英解和gbest的影响，μ的数学形式可以有很多种，本文采用了较为简单的线性表达式，公式如下：

其中：t为当前迭代次数；Tmax为最大迭代次数。

新的跟随蜂更新公式为

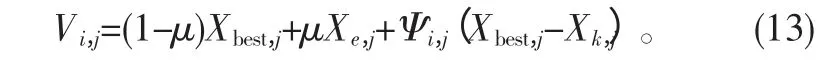
从上式可以看出，μ的取值在[0.1,0.5]之间，在算法迭代初期，精英解的影响力远小于gbest，算法向gbest快速收敛；到了算法迭代后期，随着μ值的增大，精英解逐渐平衡了gbest过大的引导作用。

在雇佣蜂阶段，为了保证普通个体有机会参与进化的过程，进一步增强算法的全局性能，以精英解为基项，随机解为引导方向得到更新公式：

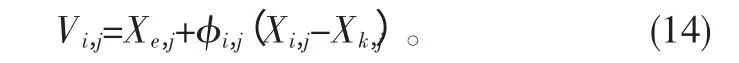
以上对ABC-elite更新公式的改进得到改进精英人工蜂群算法(IABC-elite)，相比于前者，IABC-elite在雇佣蜂阶段使用了更多个体的信息，在跟随蜂阶段突出了gbest的引导作用并快速收敛。IABC-elite算法的流程如下所示：

1）算法初始化，根据式（4）产生一个包含NP个蜜源的种群，求出精英解并将种群中每个解和精英解代入式(14)中得到新解，若适应度较高，则取代旧解。

2）跟随蜂根据式（6）所得的概率选择是否跟随，求出当前种群中的gbest、精英解和参数μ，代入式(13)中得到新解，若适应度较高，则取代旧解。

3）若种群中存在经过limit次迭代仍未改善的解，则舍弃并通过式（7）产生新解。判断是否达到最大迭代次数，是则返回历史最优解，否则返回步骤1）继续循环。

3.3 目标函数的改进

本文改进人工蜂群算法采用的适应度计算公式如下：

4 仿真和实验测试

4.1 算法有效性测试

为验证IABC-elite算法的有效性，本文采用3个标准测试函数对IABC-elite、ABC-elite、GABC及SABC算法进行仿真测试和性能对比，3个标准测试函数的定义如下所示：

测试函数和算法参数配置及不同算法的对比数据如表1～表4所示。

对于表1中迭代次数的不同，由于ABC -elite和IABC-elite对于Rastrigin函数的3000次迭代后结果相似（最优、平均精度都为0），且IABC-elite的优势之一是收敛 速 度快，故采用1000次迭代，比较效果明显。从表2 ～表4 可以看出，无论是收敛精度、收敛速度还是精度的离散程度，IABCelite 都有一定优势。

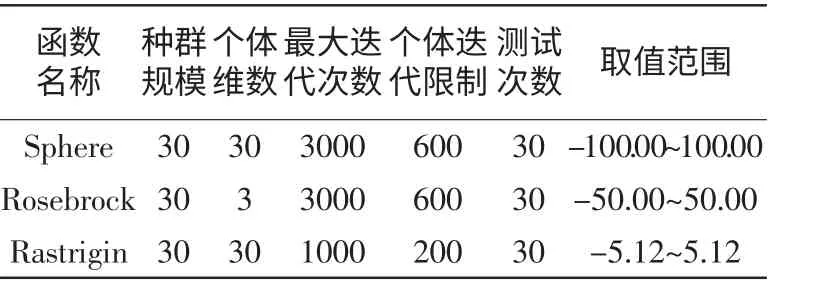
表1 测试函数及算法参数配置

表2 Sphere函数

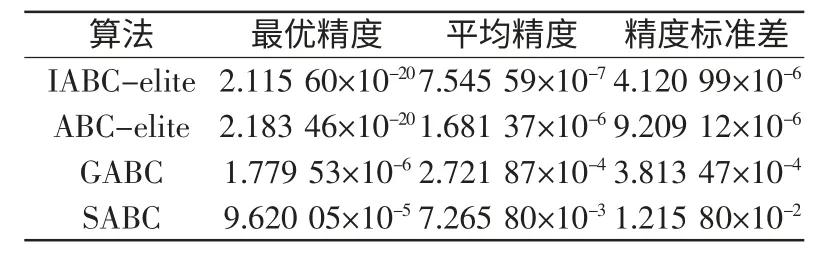
表3 Rosenbrock函数

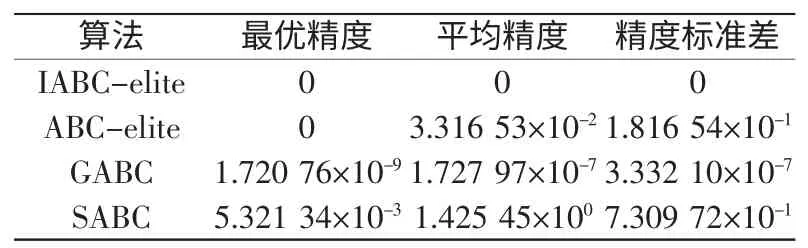
表4 Rastrigin函数

4.2 压力控制系统仿真

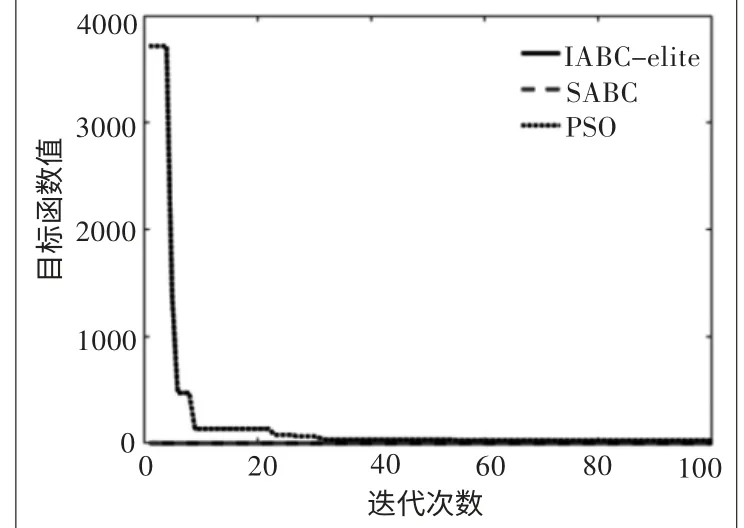
图2 几种算法的最优个体目标函数值

表5 仿真结果

本文将人工整定法、PSO、IABC-elite和SABC进行比较仿真，这里人工整定PID采用的是工程上常用的临界比例度法，仿真时间为1 s，仿真步长为0.001，简化传递函数如公式(3)所示，基本控制参数配置：种群规模SN=50，最大迭代次数MCN=100，控制参数limit=25,解的维数D=3；惩罚系数α=100，β=30，γ=10000。3种算法的目标函数的迭代过程如图2所示，仿真结果如表5所示。

从图2及表5 可以看出 ，IABC -elite 和SABC在算法迭代初期便收敛至0.1 级别，相比PSO 要迅速很多，精度也高了两个 量 级 。IABC -elite相 比 于SABC，精度提高了超过20%。IABC-elite在收敛精度上优势明显。

IABC-elite、SABC、PSO和临界比例度法在单位阶跃响应条件下的输出如图3所示。

由图3可以看出，在整个1 s的仿真时间内，采用临界比例度法和PSO得到的超调量超过20%，稳定振幅超过了10%，远大于5%的稳定标准，可以判定是振荡的。因此，从仿真结果来看，临界比例度法和PSO无法找到使传递函数达到稳定的PID参数，并不适用于电液比例溢流阀压力控制系统。

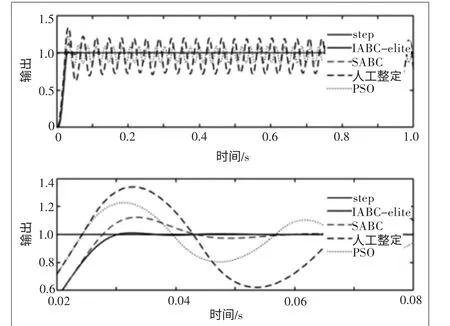
图3 几种算法的单位阶跃响应

IABC-elite和SABC都使系统达到了稳态。从整体上看，两者上升时间基本相当，但从截取的0.02～0.08 s时间段上看，相比于SABC算法，IABC-elite的超调量要小很多，也更平稳，SABC的曲线超调已经超过了10%，而IABC-elite的超调量小于1%，几乎没有振荡，动态性能相对较好。

4.3 实验测试

本文采用型号为EBG-03-C的电液比例溢流阀进行实验分析。具体参数如下：较小流量为3 L/min；较大流量为100 L/min；较高使用压力为24.5 MPa；压力调整范围为0.5～16.0 MPa；额定电流为700 mA。线圈电阻为10 Ω，滞环小于2%，重复精度为1%，质量为5.6 kg。由于实验所用液压系统的最大压力输出为16 MPa，所以压力上限为16 MPa。压力过小时，线性度和精度较差。所以，本文分别选择7 MPa、12 MPa和16 MPa压力值作为实验输入，实验结果如图4～图6所示，具体参数如表6所示。

本文在7～16 MPa的压力区间上测试了20次，测试的压力间隔为0.5 MPa，平均误差绝对值曲线如图7所示。

从图7中可以看出：当压力小于12 MPa时，误差较为稳定，基本保持在0.1 MPa以下；当压力接近压力上限16 MPa时，误差呈现逐渐增大的趋势。

5 结 论

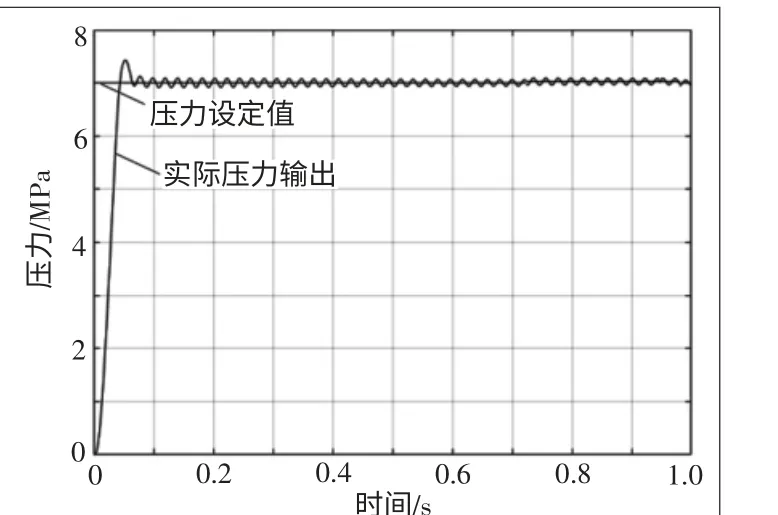
图4 设定值为7 MPa时输出

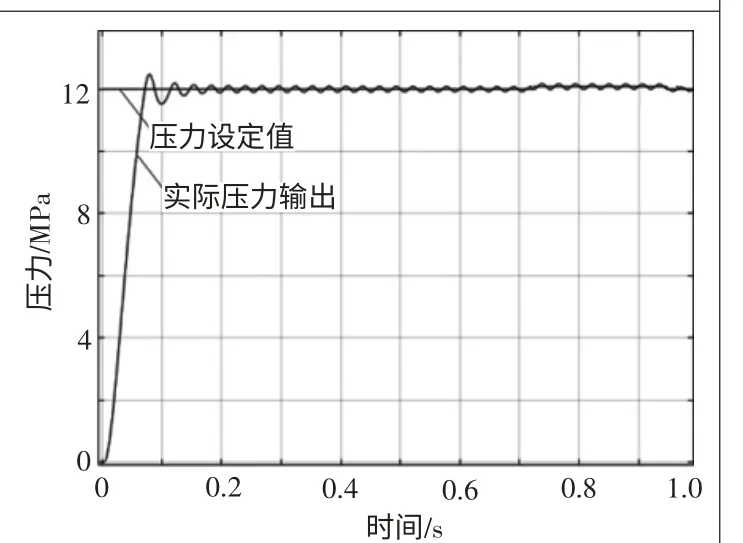
图5 设定值为12 MPa时输出

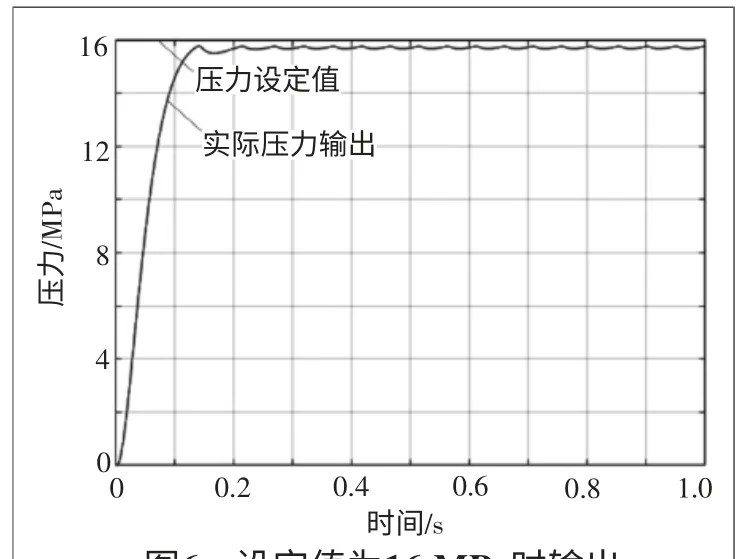
图6 设定值为16 MPa时输出

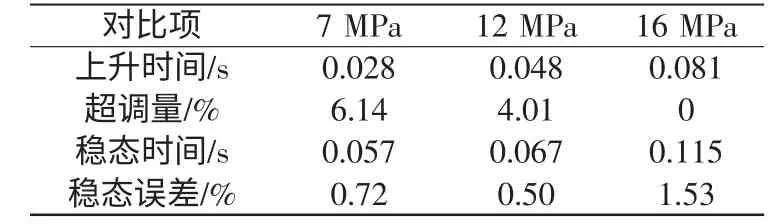
表6 不同压力等级的性能对比

本文以精英人工蜂群算法为基础，将待优化的PID 参数视为蜜源并在此之上引入系数μ，动态调整精英解和gbest的权重，加快了算法收敛速度；改进了跟随蜂更新公式，将精英个体向普通个体

图7 平均误差绝对值

引导，增强了算法的全局性能并将算法应用于电液比例溢流阀的PID控制。

仿真结果证明，IABC-elite算法相比SABC、PSO和人工PID参数整定法在系统超调、误差精度上显著减少，缩短了系统达到稳态的时间，具有一定的优越性。

实验测试表明，在可靠压力区间内，IABC-elite算法在系统的动、静态特性上表现良好，具有一定的使用价值。