液压支架立柱导向环计算方法的改进

徐文苏， 张海， 张继业， 云浩， 赵武， 范俊锴

（1.河南理工大学 机械与动力工程学院，河南 焦作454000；2.郑州煤矿机械集团股份有限公司，郑州450000）

0 引 言

随着液压支架技术的发展，液压支架最大支撑高度已达8.8 m，立柱缸径达到600 mm，这对立柱结构和可靠性的要求越来越高[1-3]。导向环作为立柱的重要支撑和导向元件，在立柱工作过程中承受着复杂的静载和动载，特别是当立柱承受较大的偏心载荷作用时，其受力状态更加恶劣。导向环在复杂应力状态下容易造成损伤，影响导向环寿命。因此，提高导向环工作可靠性对立柱性能影响很大[4-6]。目前，关于导向环设计和分析的文献还比较少。文献[7]提出了一种导向环的力学计算和分析方法，对影响导向环可靠性的因素及提高可靠性的措施进行了分析。文献[8]将导向环所受到的径向力简化为一个作用于导向环宽度中点处的集中力，对导向环的应力进行了求解。上述文献均未考虑导向环与配合面之间的间隙，且求解的是导向环沿宽度方向的平均应力。实际上，受到弯矩作用时，导向环受到的应力沿宽度方向是变化的，采用平均应力进行导向环设计时，求解出的应力值将小于实际最大应力，而且导向环工作表面与配合面之间的间隙对导向环应力也存在很大影响。故有必要对文献[8]中的导向环设计计算方法进行完善。

本文以双伸缩立柱为对象，将导向环工作表面与配合面之间间隙的影响引入到导向环设计计算中，对现有的立柱导向环设计计算方法进行完善。

1 立柱导向环应力计算方法

液压支架立柱上的导向环包括导向套导向环和活塞导向环。由于底缸、中缸、活柱及活塞、导向环等均为弹性体，故当立柱受到偏心载荷作用时，各部件的弹性变形使立柱产生一定的挠曲。如果导向环工作表面与配合面之间存在间隙（简称为导向环配合间隙），将使立柱挠曲进一步增大。

目前，在进行立柱设计计算时，往往将导向环作为弹性体，而将立柱的底缸、中缸、活柱、导向套、活塞等部件视为刚性体[8]。本文仍然沿用同样假设，但在求解导向环的变形和应力时，引入了一个新的变量——导向环的配合间隙，对文献[8]的方法进行了补充和完善。

图1为某双伸缩立柱示意图。其中，中缸活塞和活柱活塞上均有两个导向环，底缸导向套和中缸导向套上均有三个导向环。下面以中缸导向套和活柱活塞上的导向环为例，推导导向环的应力计算方法。为便于叙述，对5个导向环按照从右向左的顺序分别称为D1、D2、D3、D4、D5。其中，D1和D2为活塞导向环，D3、D4和D5为导向套导向环。每个导向环上左右两个端面中，靠近活塞腔（右侧）的端面称为前端面，另一个称为后端面。

图1 某双伸缩立柱示意图

文献[8]中，假设导向环轴断面上各点的压缩量相同，求解出了导向环沿宽度方向的平均压缩量。实际上，导向环宽度上各点的压缩量是变化的，且最大压缩量发生在前端面或后端面上。当活塞、活塞杆和缸筒均为刚体时，导向环压缩量沿宽度方向将按线性规律变化。

设导向环D1前、后两个端面的最大压缩量分别为a11和a12。同样，导向环D2～D5前、后两个端面的最大压缩量分别定义为a21和a22、a31和a32、a41和a42、a51和a52。

假设导向环D1和D2与配合表面的间隙相等，均为Δ1；导向环D3～D5与配合面之间的间隙也相等，均为Δ2。当活柱顶端受到偏心载荷作用时，该偏心载荷可看作作用于立柱中心线上的集中载荷F和作用于立柱顶端弯矩M的叠加。因为底缸、中缸、活柱、导向套等均为刚体，且导向环存在配合间隙，所以当立柱受到弯矩M作用时，活塞杆将产生刚体位移，形成初始倾角，如图2所示。而导向环为弹性体，当受到配合表面的挤压时将发生弹性变形，从而使活塞杆产生一个附加倾角。由图2可以看出，5个导向环中，D1的前端面和D5的后端面受力最大，压缩量也最大，且5个导向环前后端面上的最大压缩量按线性规律变化。因此，只要D1前端面和D5后端面的应力满足要求，导向环即是安全的。

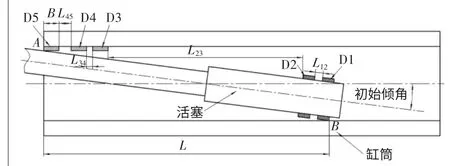
图2 导向环未压缩时的受力状态示意图

下面分别对活塞导向环D1前端面和导向套导向环D5后端面的压缩变形量及应力进行计算。

1.1 活塞导向环分析

假设在活柱顶端所受弯矩M作用下，导向环D1前端面压缩变形情况如图3所示。

1) 导向环D1前端面支反力计算。

活塞导向环的外表面为工作表面。导向环D1前端面受压后，最大压缩量为a11，如图3所示。图3中，-90°≤θ≤90°。任一位置θ处，导向环外表面到圆心的距离为ρ11θ。导向环初始外径为R1，由余弦定理得

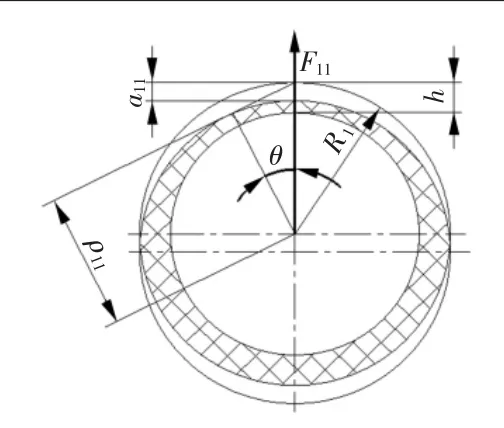
图3 导向环D1 前端面的变形示意图

式中：h为导向环初始厚度；μ为导向环泊松比。

D1前端面的支反力合力可以通过下式求出：

式中：L为导向环D1前端面到D5后端面之间的距离；文献[10] 中的Δ1和Δ2为活塞杆倾斜后活塞导向环和活塞杆导向环与配合面的最大间隙，而式(6)中的Δ1和Δ2为活塞杆倾斜前（浮动状态）的配合间隙，故式(6)中的Δ1和Δ2为文献[10]中对应值的一半。

导向环D1后端面的最大压缩量a12可用下式求出：

式中：B为导向环宽度；Δα为导向环压缩引起的活塞杆倾角增量。

则活塞杆的总倾角α=α0+Δα。由于α0+Δα是一个很小的角度，故有

同样，可求解出导向环D2的支反力及其作用点。

1.2 导向套导向环分析

导向套导向环的内表面为工作表面。活塞杆压缩导向环内表面，使其内表面呈一定的倾角。下面以D5为例，对导向套导向环的支反力进行计算。图4为D5后端面受压缩后的示意图。

1) 导向环D5后端面支反力计算。

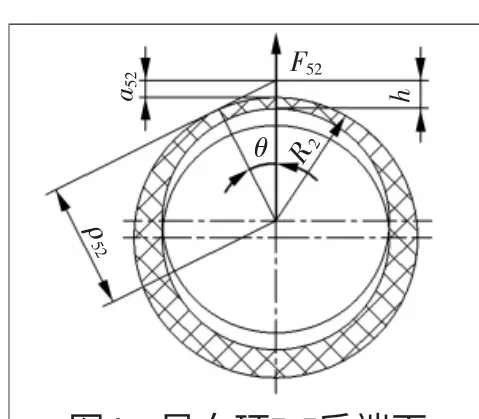
图4 导向环D5后端面变形示意图

如图4所示，导向环D5后端面的最大压缩量为a52。在任一位置θ处，导向环外表面到圆心的距离为ρ52θ，D5的初始内径为R2，由余弦定理得：

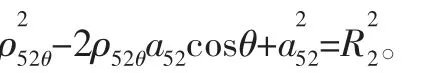
或

1.3 导向环的力平衡方程及几何方程

在应用前述方法求解5个导向环的支反力及其作用点时，首先需要求解出a11、a52和Δα。这3个变量可通过导向环力平衡方程、立柱弯矩平衡方程和立柱几何方程求解出来。

1) 导向环力平衡方程。

2 导向环应力分析

1)传统方法与本文方法的比较。

本文提出的导向环设计计算方法中，引入了导向环配合间隙和导向环宽度，可求解导向环任一端面上的应力。而传统方法求解出的是导向环宽度上的平均应力。下面以某双伸缩立柱为对象，对两种方法的计算结果进行比较。

某双伸缩立柱所受弯矩及立柱各导向环的主要参数如下：

立柱所受弯矩M=415.8 kN·m；导向环宽度H=30 mm；活塞导向环外径：中缸R1=190 mm，底缸R1=250 mm；导向套导向环内径：中缸R2=177.5 mm，底缸R2=235 mm；导向环D1与D2之间的距离：中缸L12=57 mm，底缸L12=56 mm；导向环D2到D3之间的距离：中缸L23=140 mm，底缸L23= 132 mm；导向环D3与D4之间的距离：中缸L34=12 mm，底缸L34=12 mm；导向环D4与D5之间的距离：中缸L45=44 mm，底缸L45=44 mm。导向环材料参数：弹性模量E=5800 MPa；泊松比μ=0.3。

由于传统方法不考虑导向环与配合面的间隙，故首先假设导向环配合间隙为0，求解出中缸和底缸导向环的最大应力，如表1所示。表1中，本文方法求解出的是每个导向环上的最大应力值，该应力位于导向环的前端面(活塞导向环)或后端面(导向套导向环)上。可以看出，本文方法的计算值略大于传统方法。其中，D1和D5的应力增大了11%左右，D3的应力增大了约25%。故本文方法较传统方法的计算结果更为安全。由于D1和D5应力水平较高，只要这两个导向环的应力满足要求，其它导向环也是安全的。

2)导向环与配合面之间间隙的影响。

为了分析导向环与配合面之间间隙对导向环应力的影响，以底缸和中缸为对象，以前述某双伸缩立柱的导向环宽度和间距作为基础值，并假设所有导向环的配合间隙均相等，对配合间隙为0、0.01 mm和0.015 mm三种情况下的导向环应力进行了计算，见表2。表2中列出了所有导向环的应力计算结果。表中的Di1和Di2分别表示第i个导向环的前端面和后端面。

表1 传统方法与本文方法求出的导向环最大应力值比较MPa

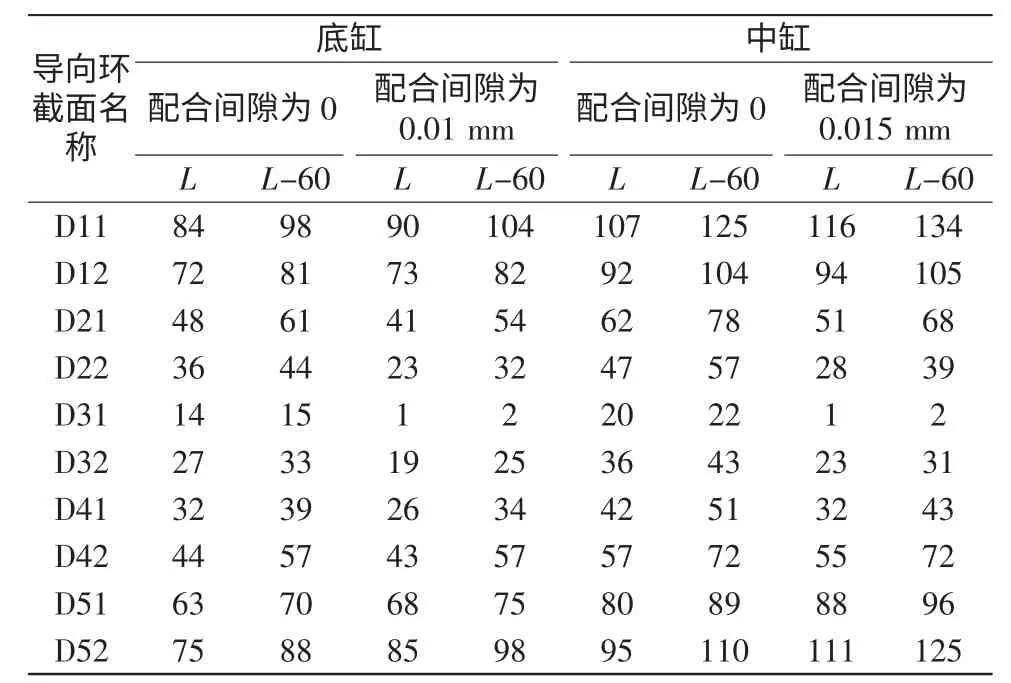
表2 导向环各个端面的最大应力计算结果 MPa

可以看出，对于底缸来说，当导向环配合间隙为0.01 mm时，D11和D52的应力较配合间隙为0时分别增大7%和13%，D21～D42的应力则小于无配合间隙时的数值。特别是D31的应力减小了93%，即该截面几乎不起支撑作用。对于中缸来说，当导向环配合间隙为0.015 mm时，D11和D52的应力较配合间隙为0时分别增大8%和17%，D21～D42的应力变化规律与底缸相同。当导向环的配合间隙进一步增大时，D11和D52截面上的应力也将进一步增大，而中间的导向环的支撑效果则逐步减弱。因此，在导向环设计时若忽略配合间隙，将使求解出的导向环应力过小。对于导向环来说，偏于危险。

3)导向环间距和宽度的影响。

导向环D1与D5之间的距离，决定了立柱固定段长度的大小，对立柱伸缩比影响很大。为了分析D1与D5的间距对导向环应力的影响，以前述某双伸缩立柱导向环D1与D5的间距L作为基础值，将L减小60 mm(其中L12、L23、L45分别减小20 mm)作为对照值，求解出各个导向环的应力，如表2所示。可以看出，如果导向环配合间隙为0，导向环间距减小60 mm后，底缸D1、D5的应力增大了17%，中缸D1、D5的应力增加了16%。对于底缸来说，当导向环配合间隙为0.01 mm时，导向环间距减小使D1、D5的应力增加约15%；与配合间隙为0时相比，D1和D5的应力分别增大了6%和11%。同样，当中缸导向环配合间隙为0.015 mm时，导向环间距减小使D1和D5的应力分别增加16%和13%；与配合间隙为0时相比，D1、D5的应力分别增加了7%和14%。

为了研究导向环宽度对导向环应力的影响，保持截面D11、D21、D32、D42、D52的位置不变，将各个导向环的另一个截面向外移动10 mm，使每个导向环的宽度由30 mm增加到40 mm。求解出的各个导向环应力，见表3。

表3 底缸导向环应力计算结果 MPa

可以看出，当导向环的宽度由30 mm增加到40 mm时，底缸和中缸导向环的应力均明显减小。其中，截面D11和D52的应力减小了19%，截面D31的应力则减小了40%以上；因此，增大导向环宽度可显著降低导向环最大应力，增强导向环的支撑和导向能力。

3 结 论

1）在求解立柱导向环的变形和应力时，引入了一个新的变量——导向环的配合间隙，推导出一个求解导向环最大应力的方法。

2）对本文计算方法与传统方法进行比较表明，本文方法求解出的导向环应力略大于传统方法。

3）当立柱所受弯矩一定时，导向环与配合表面之间的间隙越大，导向环的应力也越大。

4）固定段长度一定时，导向环宽度对导向环应力有显著影响。宽度越大，应力越小。

5）导向环宽度一定时，固定段长度越小，导向环应力越大。

综上所述，应用本文方法进行导向环设计时，求解出的导向环应力大于传统方法的计算值，有利于提高导向环的使用安全性。本文方法不仅可用于双伸缩立柱的设计，也可用于单伸缩或多伸缩立柱的设计。