量子计算在火电机组优化控制中的应用综述

2020-09-08高明明杨磊于浩洋张洪福刁友锋宋珺琤

综合智慧能源 2020年8期

高明明，杨磊*，于浩洋，张洪福，刁友锋，宋珺琤

GAO Mingming1，YANG Lei1*，YU Haoyang1，ZHANG Hongfu1，DIAO Youfeng2，SONG Juncheng3

（1.新能源电力系统国家重点实验室（华北电力大学），北京102206；2.中国华电集团天津公司，天津300203；3.华电国际电力股份有限公司天津开发区分公司，天津300270）

（1.State Key Laboratory of Alternate Electrical Power System with Renewable Energy Sources（North China Electric Power University），Beijing 102206，China；2.Tianjin Company，China Huadian Corporation Limited，Tianjin 300203，China；3.Tianjin Development Area Branch，Huadian Power International Corporation Limited，Tianjin 300270，China）

0 引言

目前，我国火电机组控制正向着智能化的方向发展，火电机组智能优化控制技术是其中的重要一环。随着智能算法的不断进步，火电机组优化控制技术与时俱进，不断提升机组的运行水平。量子计算于20世纪下半叶开始快速发展，其利用量子力学理论中的量子纠缠和量子叠加等特性，高效地对搜索问题进行求解，有助于实现机组的高性能优化控制。

量子计算最初可追溯至1982 年Feynman［1］首次提出的利用量子计算方式对量子系统演化行为进行模拟，从而实现经典计算无法处理的大规模计算量。后续的量子计算发展可划分为2 大分支:量子算法和量子衍生算法［2］。量子算法更贴近量子力学的本质，主要代表为20 世纪末提出的Shor 算法［3］和Grover 算法［4］。 Shor 算法利用量子傅里叶变换（QFT）将大数质因子分解问题转化为对函数周期的求取，借助在量子环境下高效率运行，可以实现在多项式时间内的大数分解；Grover 量子搜索算法的核心思想是利用量子叠加态原理将无序搜索问题的复杂度从N降至 N，从而极大地减少了计算量。

量子算法的大规模应用将实现计算领域的革命性突破，但量子算法必须运行在量子计算机上，不能通过传统计算机实现，目前关于量子算法的研究仍主要处于理论阶段，其广泛应用仍需等待。

量子衍生算法是量子计算的另一大实用发展方向，是量子力学与传统算法结合形成的新型算法。Kak［5］首先提出了量子神经计算，是量子衍生计算技术的发展开端，Kouda等［6］在此基础上进一步提出了量子神经网络的概念。随后，量子衍生算法不断发展并被引入智能算法领域，陆续出现了量子衍生模拟退火算法、量子衍生遗传算法等。量子衍生算法本质上仍属于传统算法，因此可以直接在传统计算机平台上执行，目前已在众多领域有所应用［7］，本文所论述的在火电机组优化控制中的应用和发展均为量子衍生算法。

本文首先对量子计算的基本特征进行介绍，文中综合讨论多种量子衍生算法在火电机组优化控制中的应用形式和改进方法，并介绍其各自前沿研究的应用领域，最终展望量子计算在该领域的可能发展方向，为后续量子计算在火电机组优化控制领域的发展应用提供参考。

1 量子计算基础

1.1 量子比特和量子叠加态

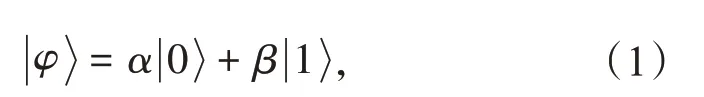
式中:α和β为复数，称为概率幅。

α和β需满足以下要求

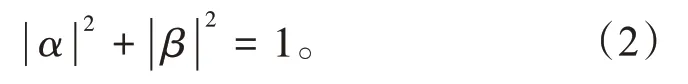
以遗传算法（GA）为例，典型GA 的染色体表示方式为

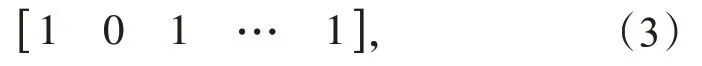
即通过二进制比特序列的方式表示优化问题的一个潜在可行解。但在量子遗传算法（QGA）中，量子染色体序列以量子比特序列的形式构成

根据式（1）、式（2）的规则，此时由式（4）所表示的染色体将同时处于2n种叠加态中，各状态间可实现并行进化，因而与传统GA 相比极大地增加了种群的多样性，在搜索过程中存在巨大优势。

1.2 量子门

量子门是用于实现量子比特相位改变的机构，量子门的种类多样，常用的有量子旋转门、泡利-X门（非门）、Hadamard 门等，以量子旋转门为例，其定义为

旋转门作用于单位量子，使其概率幅发生改变

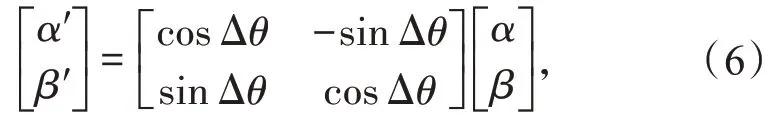
式中:θ 为旋转变异角；α'和β'为相角偏移后的概率幅，α'和β'依然需满足式（2）的要求。

在迭代过程中对θ 进行控制，可实现对量子染色体种群的定向进化控制。

量子叠加和量子门的概念是量子计算中的重要基础，相当一部分量子衍生算法采用其作为设计的核心。伴随着量子计算在优化控制领域的深入应用，更多基于深层次量子计算原理的算法也在不断发展中。

2 量子计算在火电机组优化控制中的应用

随着我国电力行业清洁化和智能化的发展，智能优化控制技术迅速兴起，在火电机组优化控制中，粒子群算法、蚁群算法、遗传算法等多种智能优化算法都实现了成熟的应用；同时，伴随着人工智能技术的爆发，机器学习算法也迅速融入该领域。但是，常用的智能优化算法和机器学习算法均存在不同程度的缺陷，如计算效率低、易陷入早熟或参数繁多不易确定等，对算法在训练和寻优过程中的效果影响极大，对这些因素的处理是否得当，将直接影响优化结果。

量子衍生算法为解决以上问题提供了一种思路，量子计算远胜于经典计算的并行搜索性适用于大规模数据运算，可极大地提升原算法的运算效率和寻优能力，实现优于传统算法的控制效果。

2.1 量子粒子群优化算法的应用

2.1.1 2种不同量子粒子群优化算法

粒子群优化（PSO）算法是典型的群智能优化算法，基于对鸟类群体捕食过程的模拟。PSO 算法应用简单、收敛速度快，但在优化过程中，由于粒子在n 维空间中以有限轨迹运动进行搜索，不能保证对整个解空间完全遍历，因此传统PSO 算法不是严格的全局收敛算法［8］。孙俊［8］和李士勇等［9］结合量子计算理论，于同一时期分别提出了2 种不同的量子粒子群优化（QPSO）算法，以解决传统PSO算法中存在的问题。

李士勇等提出的QPSO 算法（以下简称李QPSO算法）采用典型量子计算方式，将粒子速度更新转化为旋转门转角更新，位置矢量更新转化为概率幅更新，并利用量子非门进行变异，以进一步提高粒子群种群的多样性。

孙俊提出的QPSO 算法（以下简称孙QPSO 算法）基于δ 势阱模型，根据“量子空间内粒子的速度和位置不能同时确定”这一特性，以波函数的方式描述粒子状态，舍去了算法中粒子速度这一参数，简化了计算形式和算法参数并提高了算法的全局搜索能力。

有试验认为［10］，孙QPSO 算法在运算效率和搜索能力上具有优势，其模型参数更少，实现方式简单，因此孙QPSO 算法目前的应用和发展范围更广，也是目前火电机组优化控制中应用最广泛的量子衍生优化算法。

2.1.2 在PID整定中的应用

孙QPSO 算法首先应用于控制回路的比例-积分-微分（PID）参数优化中，典型的应用方式如图1所示。算法应用于超临界机组主汽温度串级控制系统仿真，对外回路PID 控制器参数进行整定，结果表明，系统经参数优化后控制品质有所提高［11］。

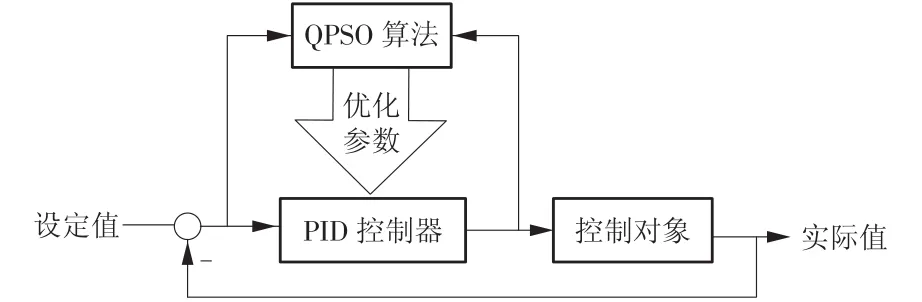
图1 QPSO算法在PID控制器整定中的典型应用方式Fig.1 Typical application of QPSO algorithm in PID controller tuning

后续有学者［12］分析认为，孙QPSO 算法在机制上仍具有陷入局部最优的可能性，为解决这一问题，向算法中引入扰动变异，克服粒子在进化中后期的早熟现象。改进后的QPSO 算法在主汽温PID控制器的整定试验中得到了验证，使系统调节时间缩短，超调量变小。这一改进算法进一步应用在再热汽温调节系统PID 参数优化中，优化结果良好，与传统QPSO算法相比，有效缩短了寻优时间［13］。

2.1.3 基于混沌理论的QPSO算法改进

孙QPSO 算法具有高效的寻优能力，但在搜索后期同样可能因粒子聚集导致搜索能力下降，这也是PSO 算法的常见问题。常见解决方式是向QPSO算法引入混沌搜索机制，构建混沌粒子群优化（CQPSO）算法，混沌系统的伪随机性和遍历性可以一定程度扩大粒子群在优化后期的搜索范围和搜索均匀性，遏制局部最优现象的出现。CQSPO 算法用于某600 MW 机组主汽温控制系统的辨识和参数优化中，具有和传统PSO 算法基本一致的结果，但在多模态、高参数量的情况下具有更快的搜索速度和成功率［14］。CQPSO 算法继续应用于循环流化床（CFB）机组大延迟对象的PID 控制器参数二次优化中，其效果明显优于使用经验公式和传统PSO 算法的效果［15］。

以上研究表明，引入混沌机制是QPSO 算法寻优能力下降时可首先采取的措施。

2.1.4 在系统辨识中的应用

部分学者对孙QPSO 算法中的粒子状态更新方式进行了改进，以提高粒子搜索的随机性，强化粒子群的遍历能力［16-18］。改进的QPSO 算法用于对超超临界机组主汽温控制系统进行辨识，可以获得比传统PSO 算法和原QPSO 算法更加精确的主汽温控制模型。近期有学者向QPSO 算法中加入引力作用机制，提高算法的进化速度和对最优值的逼近能力，实现对600 MW 机组喷氨脱硝系统的有效预测，可为后续优化控制提供基础［19］。QPSO 算法同样对热工系统辨识表现出广泛的适用性，采用QPSO 算法对1 000 MW超超临界机组多个子系统进行辨识，均获得了较为精确的结果［20］。

QPSO 算法在火电机组系统辨识应用中展现了良好的效果。高精度辨识模型的建立将助于系统优化控制的设计，从而提高系统的控制品质，是值得进一步推广的应用。

2.1.5 2种QPSO算法的联合使用

李QPSO 算法在火电优化控制中应用较少，其特点是可以提高粒子群搜索的精细度。黄宇等［21］采用李QPSO 算法并结合混沌序列对初始种群进行多样化优化，进行循环流化床机组煤量-床温模型和风量-床温模型的辨识，模型精度极高且迭代次数较少。

双量子粒子群优化（DQPSO）算法［22］结合了孙、李QPSO 算法的特点，对粒子个体和种群进化方式同时进行了量子化，在多个寻优测试中均获得了优于原始孙、李QPSO 算法的结果。这种新型综合算法未来可能成为火电机组优化控制领域的前沿算法。

2.1.6 QPSO算法小结

以上研究成果表明，QPSO 算法及多种改进型算法［23］可适用于火电机组系统优化，或进行系统辨识为后续控制系统的设计和优化提供基础。该算法成熟且应用广泛，目前仍具有很大的发展空间。

2.2 QGA的应用

2.2.1 QGA在应用中面临的困难

QGA 是火电机组优化控制领域中量子衍生算法的另一主要应用分支。QGA 形成时间相对较早［24-25］，利用量子染色体编码和量子旋转门实现种群的迭代进化，在缩小种群规模的同时提高了算法的搜索效率。目前，QGA 可能不适用于连续函数的优化问题，试验表明［26］，单纯的QGA 在一些优化问题中甚至可能逊于传统GA 和模拟退火遗传算法（SAGA）。实际应用中QGA 常需进行适当改良，使其适用于特定问题。

2.2.2 针对旋转变异角的改进

QGA 的常见改进方式之一是针对量子门旋转变异角的调整策略进行改进，根据模糊推理规则自适应地调整进化过程中的旋转变异角。这种改进方式可以提高收敛速度，对某循环流化床机组的一次风-床温模型进行了有效辨识［27］。采用相似思路改进旋转变异角调整策略，可以实现对分数阶PIλDμ控制器进行整定［28］，进一步证明改进后的QGA 可应用于复杂热工系统的参数优化。

目前，针对QGA 旋转变异角调整策略的改进方式并不唯一，实际应用中可进行灵活的设计，采用适用于具体问题的调整策略。

2.2.3 小生境技术与混沌变异机制的引入

为解决CFB 锅炉汽温时变、大滞后和大惯性的控制难点，有学者［29］采用了自抗扰控制方式（ADRC），其控制效果优于传统的PID 控制，但参数更多，整定也更加困难。采用QGA 对ADRC 参数进行整定，并引入小生境进化策略和混沌变异机制提高QGA 种群间的竞争行为和多样性。试验表明，这一改进取得了极佳的优化控制效果，证明了量子优化算法与其他控制策略结合共同用于优化控制的可行性。

2.2.4 QGA小结

以上实例表明，QGA 未来在火电机组优化控制领域仍具有广阔的发展前景，通过引入合理的改进机制，QGA 可广泛应用于各种热工系统辨识、参数优化问题中。

3 量子计算在其他算法中的应用

3.1 在其他智能优化中的应用

目前，其他量子智能优化算法在火电机组优化控制领域的应用较少，尚处于研究起步阶段，对这一方面的应用和研究可能具有很大前景，如量子退火算法（QA）、量子免疫算法（QIA）等。目前，不断有新型的量子群智能优化算法诞生并逐步应用于火电机组优化控制领域，尤其以量子群智能优化算法居多，如量子自适应鸟群算法（QBSA）［30］、量子灰狼优化（QGWO）算法［31］、量子同步鲸鱼优化（QSWO）算法［32］以及量子迭代混沌涡流搜索（QIVS）算法［33］等。这些算法的诞生和应用，预示着量子计算在火电机组优化控制领域蓬勃发展的前景。

3.2 采用量子计算优化的机器学习算法

得益于计算能力和互联网技术的高速发展，机器学习（包括深度学习）算法发展迅速并广泛应用于实际工程。在火力发电领域，聚类算法、支持向量机（SVM）和神经网络等机器算法的应用为机组优化控制提供了新的方法。同时，基于量子计算高性能寻优能力和机器学习算法优秀函数逼近能力的新型应用方式也陆续出现，并可能在未来出现突破式的发展。

目前，常见且有效的一种方式是联合使用量子优化算法和机器学习算法，用以解决机器学习算法在工程应用中的参数整定问题，从而大幅提高算法的建模精度，如图2所示。

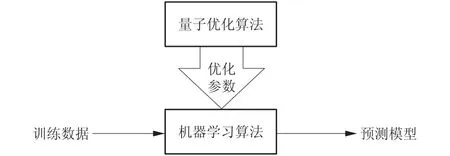
图2 量子优化算法与机器学习算法的联合使用方式Fig.2 Joint use of quantum optimization algorithm and machine learning algorithm

例如，径向基函数（RBF）神经网络可以有效辨识热工系统，但RBF 网络具有隐含层参数较多的问题，可以采用QGA 对RBF 网络的参数进行估计，优化后的RBF 网络可以实现对多种热工过程的有效辨识［34］。近期有学者［35］采用差分进化量子粒子群优化（DE-QPSO）算法对超限学习机（ELM）的网络参数进行优化，成功提高了ELM 的泛化能力，实现了对超超临界机组NOx排放量的较高精度预测。另有学者［36］应用QPSO 算法对最小二乘支持向量机（LSSVM）的核函数参数进行优化，对某机组主汽温控制系统的建模证明这一策略的预测精度可超过反向传播（BP）神经网络。

3.3 量子计算与机器学习算法的直接结合

除以上常用的优化方式外，量子计算与机器学习算法正逐渐实现融合式发展，形成新型的量子机器学习算法，如图3 所示。这类新型算法已在火电机组优化控制领域初步应用，并不断发展与完善。

采用结合量子计算与深度学习技术的样本增量量子神经网络（SIQNN）建立锅炉NOx排放质量浓度和煤耗模型，并在此基础上通过量子人工蜂群（QABC）算法对锅炉运行参量进行优化，降低不同负荷下的NOx排放质量浓度和煤耗，该系统已成功应用于某330 MW 煤粉炉机组［37］。另有结合量子力学与快速学习网络（FLN）提出的量子双并行前馈神经网络（QIDPFNN），可以建立精准度更高的CFB 机组热效率与NOx排放模型，被证明具有比FLN 和ELM等传统算法更强的泛化能力和稳定性［38］。

量子机器学习算法的研究和应用将逐渐成为未来算法研究领域的热门学科，量子机器学习算法的工程应用也标志着火电机组优化控制领域的一次革新，未来势必有更多高效能的量子机器学习技术逐步应用于这一领域，为提高火电机组控制水平做出贡献。量子机器学习算法的产生并不表示传统联合使用方式被取代，二者将形成并列式发展。