基于修正主应力旋转理论的抗滑桩桩间土绕流计算方法

向先超，陈 鑫，沈亚伦，瞿 茹，刘佳豪

（中国地质大学（武汉）工程学院，湖北 武汉 430074）

1 研究背景

随着大量水利工程的兴建，形成了许多大型边坡，国家和地方投入了大量的人力和物力来进行这方面的研究和治理。抗滑桩是边坡治理的一种重要方法，而桩间距的确定是抗滑桩治理工程中的一个重要问题，一般来说，桩间距太小会造成工程浪费，桩间距太大则可能造成三种抗滑桩失效问题，即单桩承担的滑坡推力过大时桩的折断、桩间无挤土效应时土的绕流和桩前土抗力不足时桩的倾倒。因此在抗滑桩设计时必须进行三种验算：桩的内力验算、滑坡整体滑动验算和桩间土的绕流验算。

桩的内力验算与滑坡整体滑动验算方法相对而言较为成熟，而桩间土的绕流验算方法研究则处于起步阶段。桩间土的绕流是一个三维问题，由于目前对作用在抗滑桩后滑坡推力分布模式仍采用矩形、三角形、梯形等假设[1]，从三维方面研究桩间土绕流难度较大，所以大多从二维平面土拱效应出发，以桩间土拱的稳定来判断桩间土是否发生绕流，即“考虑土拱效应的桩间距确定方法”，这类研究[2-3]大都将抗滑桩后土拱效应看成“拱结构物”，符合结构力学中的合理拱轴线方程，采用拱结构力学传递机制，以拱结构破坏条件建立静力平衡方程。笔者[4-5]采用离散元方法分析了土拱效应的形成及发展机制，实际上“拱结构物”假设与土拱效应相差较大，土拱效应起源于颗粒物质中的粮仓效应，主要描述散粒体物质中由于颗粒间的摩擦导致的应力转移现象，由“拱结构物”假设提出的计算模型依据不同的强度准则，与土拱特征提出的模型计算结果相差甚远。

为弥补“拱结构物”的不足，本文将Terzaghi 土拱理论[6]（又称松动土压力理论，本质是微分单元模型，又称水平层模型）应用于抗滑桩，提出修正主应力旋转理论，建立极限状态下桩的荷载分担比计算模型，提出相应的桩间土绕流计算方法。

2 Terzaghi 土拱理论在抗滑桩设计计算中的应用

Terzaghi土拱理论由Janssen 连续介质模型发展而来，Janssen模型中作用在粮仓底部的饱和压力为：

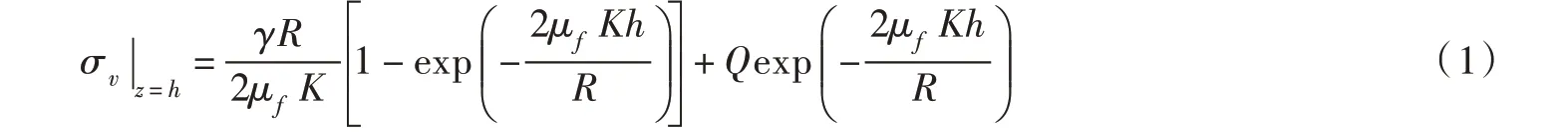
式中：σh为横向应力；σv为竖向应力；K为应力转向比，定义为K=σh/σv，在土中则为侧向土压力系数；γ为土的重度；μf为颗粒与壁的摩擦系数；R为圆柱形粮仓的半径；Q为作用在粮仓表面的均布荷载；h为粮食堆积高度。

式中：c、φ分别为土体内摩擦角与黏聚力；B为活动门宽度；H为土拱高度。

与粮仓效应不同的是，活动门试验中土能充分发挥自身抗剪强度的高度（即土拱高度H）要小于土的堆积高度h，Terzaghi建议H取1.5B，因此活动门试验中的超载Q为：

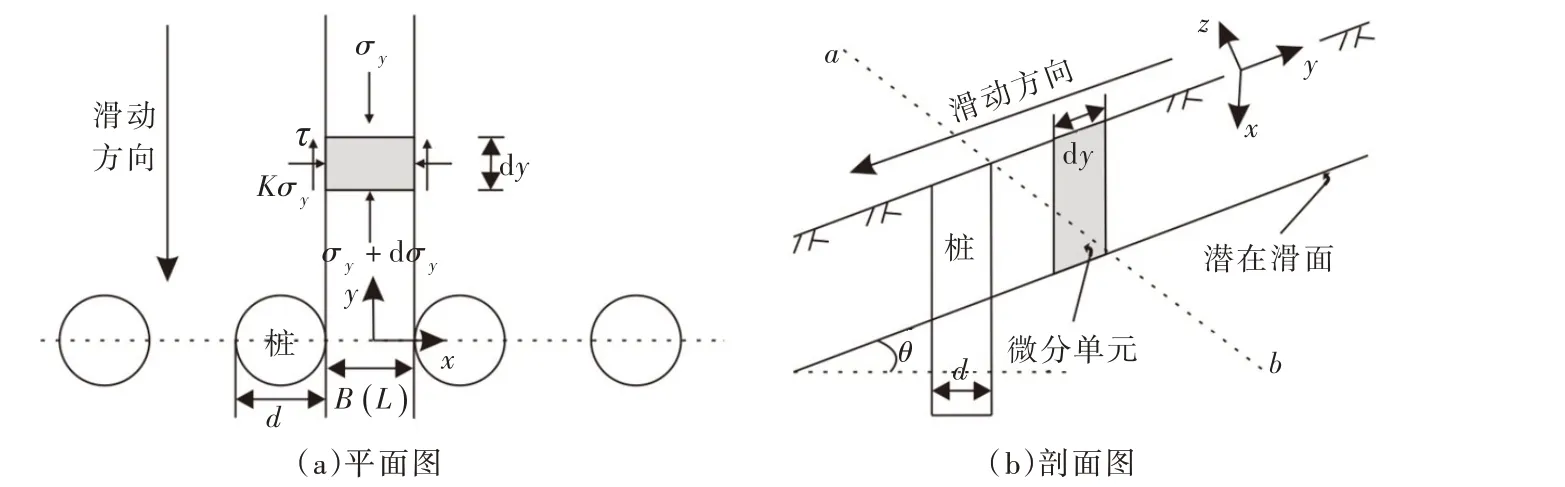
图1 边坡中的土拱效应

Bosscher[8]将活动门试验结论引入边坡-抗滑桩体系，提出如图1所示的桩后土拱模型，将桩间土视为活动门之上的屈服土体，则B=L，抗滑桩可视为活动门两旁的固定基础，即桩径d 视为固定基础。抗滑桩后土拱的超载Q为：

式中：q为滑坡剩余下滑力；N为土的重度滑沿滑动面倾角方向的分重度；L为桩间净距；NH为土拱自身剩余下滑力。

N表示如下：

式中：θ为滑动面倾角。

对于矩形截面抗滑桩，桩截面长度为b，桩间净距为L，水平微分层受力分析如图2所示，y方向受力平衡，则有：

式中τ为为剪应力。

τ表示如下：

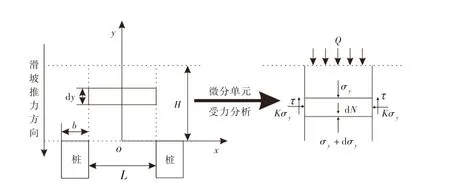
图2 微分单元受力平衡分析

式中：超载Q为拱后剩余下滑力，由式（4）与式（5）确定。土拱高度H采用活动门试验经验关系，即H=1.5L，且相对于整个坡体长度来讲，土拱高度H较小，土拱自身剩余下滑力NH可忽略不计，建议式（4）中NH 取0，Q 取滑坡剩余下滑力值q，由此桩的荷载分担比ξ可表示为：

式中：ξ为桩承担的荷载与桩土承担的总荷载之比，是表示土中应力转移至桩的大小的量，反映土拱效应强弱，意义与桩土荷载分担比一致。

3 基于修正主应力旋转理论的侧向土压力系数

Terzaghi 土拱模型分析方法中，侧向土压力系数是微分单元中各点K值的平均值，用表示。由于土拱效应的存在，主应力发生旋转，是微分单元各点K值求平均，只有当σh、σv均布、主应力不旋转时才有，因此主应力旋转理论的关键在于的求解。

3.1 修正的主应力旋转理论Handy 提出，考虑墙土摩擦时，主动状态下的墙土接触点的侧向土压力系数可表达为：

式中：θ为小主应力与水平方向的夹角，大小与墙土摩擦角δ 相关。

使用水平微分单元方法时，由于竖向应力不再均布，Handy 提出用平均竖向应力σav代替σv，表示为：

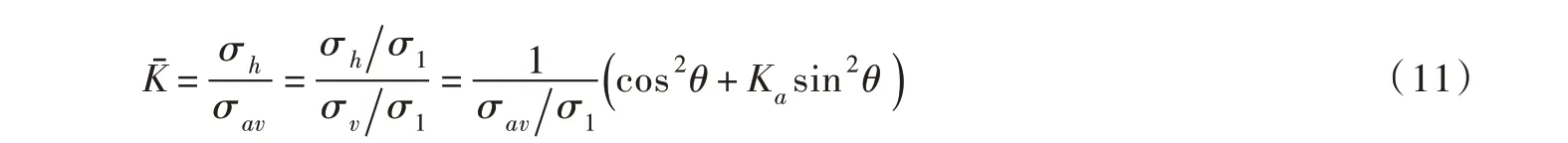
式中σav/σ1由迹线的形状确定，有：

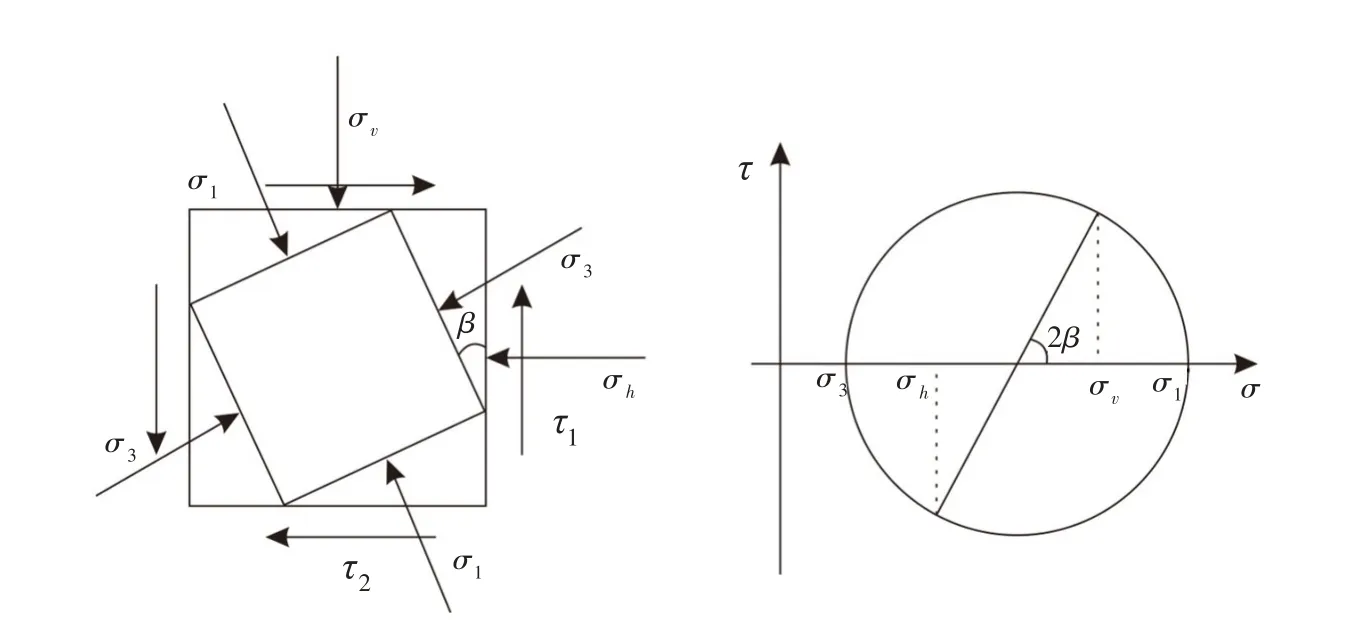
图3 主应力旋转下的侧向土压力系数分析

实际上主应力的旋转使σh、σv都不再均匀分布，用仅考虑σv变化的式（11）研究挡土墙非线性土压力问题时会导致水平方向静力不平衡，为解决此问题，挡墙领域出现了从改变滑裂面[13]与增加水平微分单元间剪应力[14]来平衡水平应力的方法，也未从根本上解决此问题。基于此，本文对式（11）做出修正，将以往研究中主动状态下的小主应力与水平面的夹角、被动状态下的大主应力与水平面的夹角，统一为主应力旋转角β，如图3所示，主应力与旋转角β之间的关系为：

根据第一应力不变量有：

联立式（13）与式（14）可得土中一点K的表达式：

当土体处于极限应力状态下时，有σ3σ1=Ka，式（15）则变为：

此时K 仅与主应力旋转角有关，本文定义β ∈(0°，45°)为主动状态，β ∈(45°，90°)为被动状态当旋转角β=0时，K=Ka；当β=90°时，K=Kp；当β=45°时，有σh=σv，K=1，此时水平方向与竖直方向没有剪应力，为静水压力状态。若建立图2所示的坐标系，微分单元中的侧向土压力系数则为：

3.2 主应力旋转角与主应力迹线由式（15）可知，K与主应力旋转角β和实际应力状态σ3/σ1两个因素有关。应力状态σ3σ1代表土内摩擦角的发挥程度，最大为土体的抗剪强度，其大小与土的位移有关，在静止状态K0与极限状态Ka、Kp之间变化，当位移足够大时，可达到极限应力状态，式（15）则变为式（16）。β表示应力转移的程度，也与竖直方向、水平方向的剪应力大小相关。

4 水平微层侧向土压力系数求解

关于桩-土作用极限分析方法，现认可度较高的有三种：楔体滑动法[19]、绕流阻力法[20]、Ito的塑性变形理论法[21]，不同的方法适用于不同的桩距。矩形截面桩下的塑性变形理论法如图4，De Beer等[22]和Poulos 等[23]分析塑性变形理论时，得到桩间距为桩径的2.5～5倍下的计算结果才与试验符合较好。b/L较大时，计算结果过大，大大超过了桩的抗弯强度，b/L较小时，土体不能自稳，原因在于破坏面与y方向的夹角α 并不是定值，而是随桩间距变化的量。

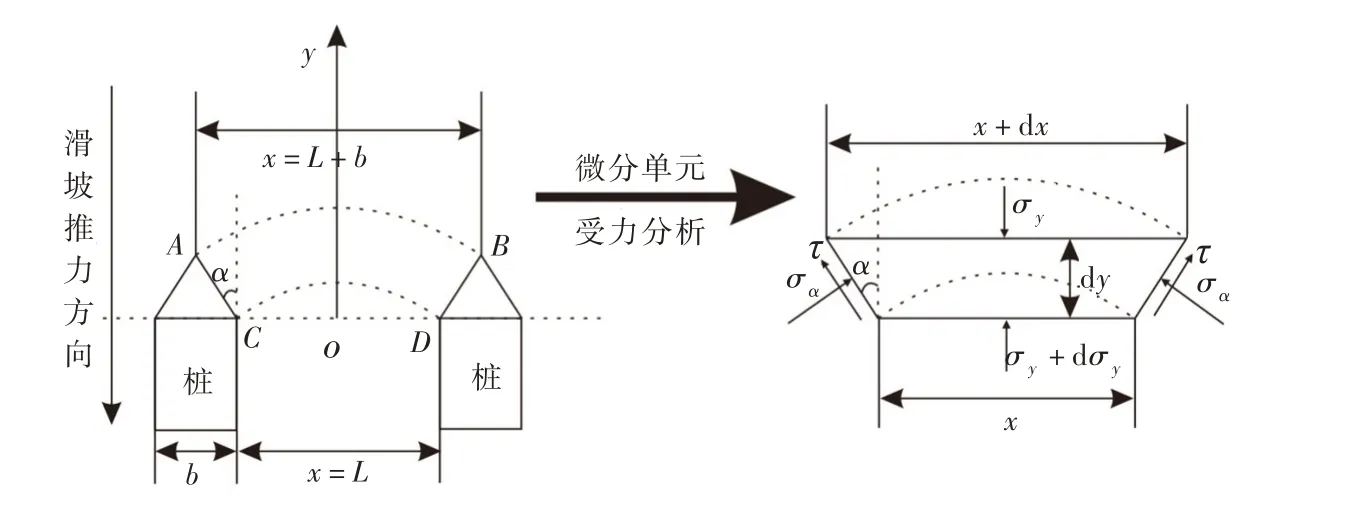
图4 矩形截面桩中的塑性变形理论

本文对此做出改进，根据莫尔-库伦准则，可将破坏角α的变化描述为主应力方向的变化，用主应力旋转角β表示，因此塑性变形理论只是某一特定桩距下的桩土极限破坏模式，在这一桩距下有α=45°+φ2，βL=90°（βL是β 在竖直向假设破坏面上的值），可定义这一特定桩距为Lmin，此时符合塑性变形理论中K=Kp的假设，如图5（a）所示。随着桩间距逐渐增大，βL逐渐由90°减小到0°，当βL=0°时，土体已不能自稳，为主动朗肯式破坏，K=Ka，可定义这一桩距为Lmax。如图5（c）所示。

随着桩间距的增加，桩后土体极限破坏逐渐由被动变为主动，定义由被动向主动转换的桩距为L0，假设βL随桩距增加而均匀减小，那么主应力旋转角与桩间距的关系可表示为：

当L＜Lmin时，桩土极限破坏不再为图5所示，Ctpoгahob 等[24]认为桩后塑性变形不再局限于桩端，而会向桩后延伸，形成图6（a）所示的对数螺旋破坏面，这也揭示了Ito理论在小桩距下不适用的原因。在工程实际中，土体是三维空间体，不会发生图6（a）所示的对数螺旋破坏，而是发生沿图1（b）中的ab线所示的竖直方向上的破坏，即滑动楔体法[19]破坏模式，Lmin为滑动楔体法适用的临界桩距，根据散粒体极限平衡理论Lmin有：

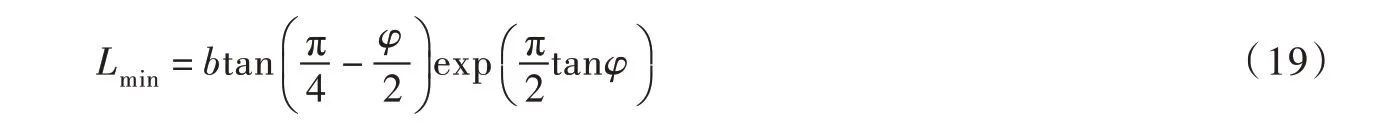
当L＞Lmax时，桩与桩之间无相互影响，桩土极限破坏为单桩绕流破坏模式，如图6（b）所示，沈珠江[20]提出临界桩间距为：

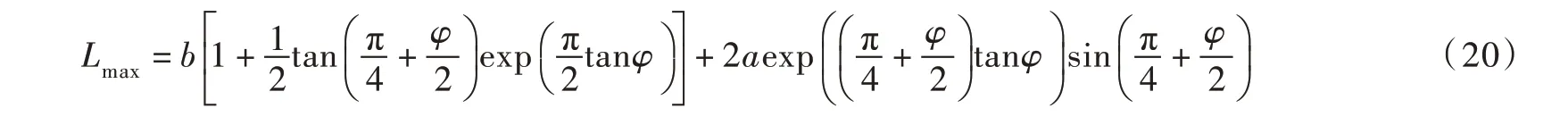
式中a为桩截面宽度。

如果不考虑桩侧面阻力，即a=0时，Lmax可表示为：

将式（19）、式（21）代入式（18），有：

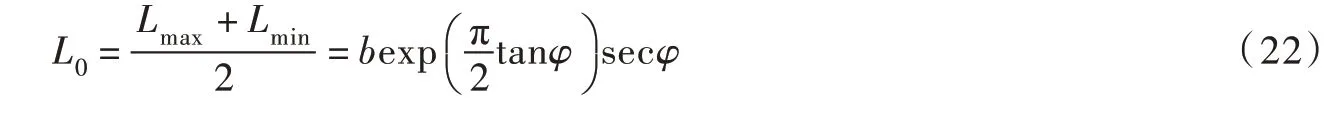
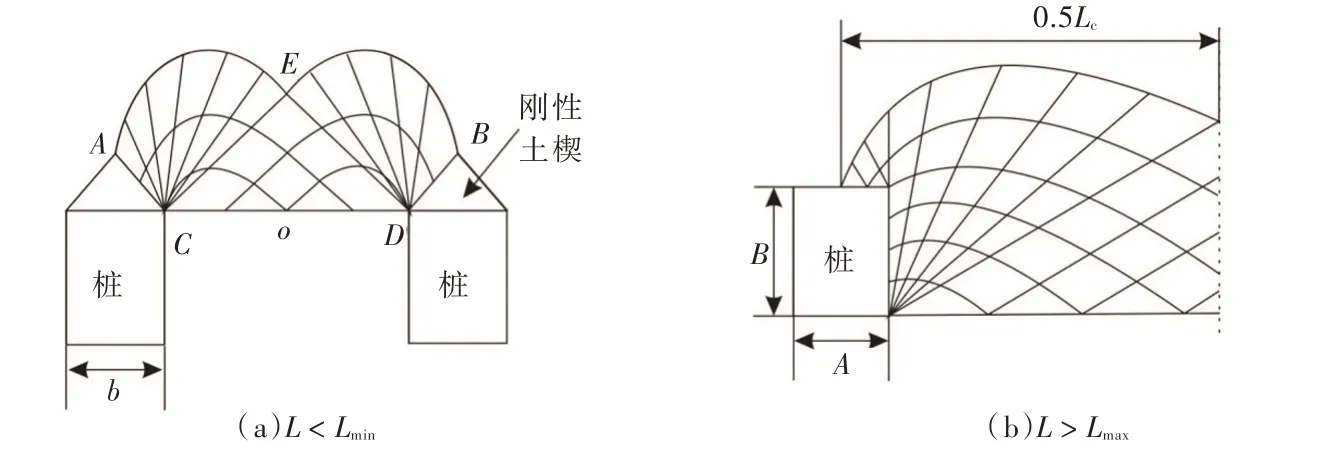
图6 两种桩-土极限破坏模式

当L ∈(Lmin，L0)时，极限荷载下的桩后土体处于被动状态，可用抛物线型大主应力迹线描述，建立笛卡尔坐标系如图5（b）所示，根据对称关系x=0，dydx=0，可设方程为：

且方程满足下式：

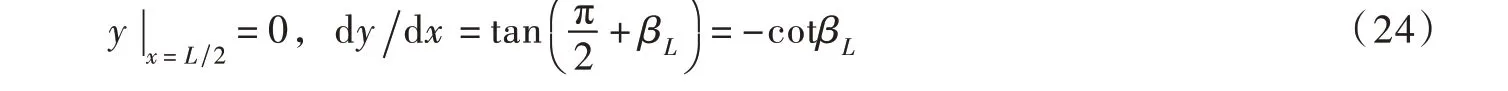
联立式（23）、式（24）求得抛物线方程：

方程两边同时对x 微分，可得到主应力迹线上主应力旋转角β随坐标x的规律表达式：

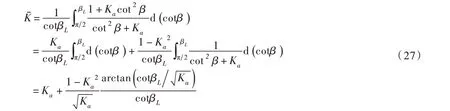
当L=Lmin时，需对式（27）取极限有：

当L ∈(L0，Lmax)时，桩后土体处于主动状态，用小主应力迹线描述，根据对称关系x=0，dydx=0，依然可设方程式为（23），且方程满足下式：

将（29）代入式（23）求得抛物线方程：

可得到主应力旋转角β随坐标x的关系：

当L=Lmax时，需对式（32）取极限，有：

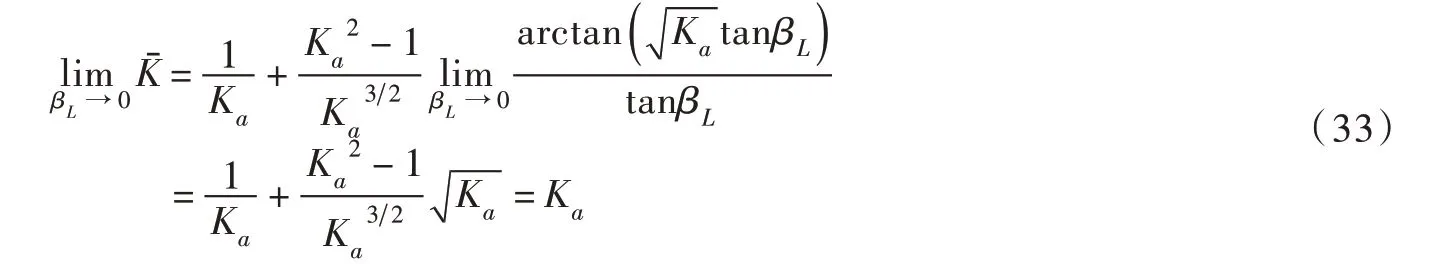
将式（26）、（32）代入式（8）求得桩间土应力表达式，进而代入式（9）即可求出桩的荷载分担比。方程与桩间距、桩后推力荷载有关，采用极限应力状态假设时，则只与桩间距变化相关。

5 桩间土绕流计算

抗滑桩后土体通过土拱效应将应力转移至桩上，这种应力转移通过土体抗剪强度实现，土体自身强度不足时，桩间土发生绕桩流动，因此土体在极限状态下时，应力迁移的程度最大，桩的荷载分担比最大。由此可得出判定桩间土绕流验算新方法：将桩间土稳定性系数定义为极限荷载下桩的荷载分担比与实际荷载下桩的荷载分担比之比，稳定性系数大于1则桩间土稳定，不发生绕流，小于1时，桩间土有绕桩流动趋势。

由于实际荷载下桩后土体处于非极限状态，主应力迹线上的实际应力状态σ3σ1处于极限状态与静止状态之间，与土颗粒间位移相关，难以确定，因此定量地描述桩后土体的非极限状态还较为麻烦，建议根据工程实测确定实际荷载下桩的荷载分担比。因此本文方法适用于已有的抗滑桩工程桩间土稳定性监测预警，并在已有相关实际工程监测资料积累的基础上，对类似抗滑桩工程设计进行桩间土稳定性验算。下面对建立的极限桩荷载分担比模型计算结果与数值模拟结果进行对比分析。

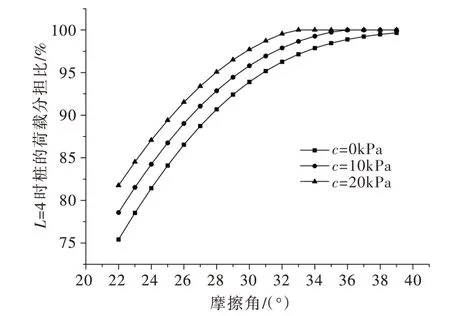
图7 土的强度参数对桩的荷载分担比的影响

5.1 土体性质对桩的荷载分担比的影响假定滑坡剩余下滑力q=200 kPa，桩截面长度b=2 m，取3组黏聚力分别为：c=0 kPa、10 kPa、20 kPa；桩间净距L=4 m ；内摩擦角φ则在22°～39°之间变化（保证L＜L0处于被动状态），计算时可视式（4）中土拱自身剩余下滑力NH=0，则拱后超载Q=q。

计算结果如图7，由图可知，土体强度参数c、φ值越大，桩的荷载分担比越大。用式（4）计算桩间土荷载时，可能出现负值的情况，桩的荷载分担比会大于100%，这是因为桩间距很小时，黏聚力不需全部发挥，土的荷载就已全部转移至桩。

5.2 桩间净距对桩的荷载分担比的影响假定黏聚力为定值c=20 kPa，取3组内摩擦角分别为：φ=20°、25°、30°，计算不同φ 下的临界桩间净距，即土拱效应存在范围L ∈(Lmin，Lmax)，并与文献[25]数值模拟结果对比。

由图8可知，理论计算结果与数值模拟结果虽未完全吻合，但符合其大致变化趋势：随着桩间净距L的增大，桩的荷载分担比显著降低。同一曲线上，在桩间净距L=L0附近桩的荷载分担比有较大的跨越，跨越幅度随内摩擦角的增大而增大，原因在于主应力迹线上的点并非全部处于极限状态，导致被动状态下结果偏大，主动状态下结果偏小，因此使用本文方法计算桩的荷载分担比，建议被动状态下取值适当减小，主动状态下的取值适当增加。

图8 桩间净距对桩的荷载分担比的影响

本文对极限桩荷载分担比模型计算结果与数值模拟结果进行了对比分析，在后续抗滑桩工程中可以通过抗滑桩桩土应力的全过程监测，利用前面建立的模型计算极限荷载分担比与监测的实际荷载分担比的比值，对抗滑桩工程的绕流稳定性进行评价和预警。积累一定的实际工程监测数据后，将可以用于后续类似抗滑桩工程设计的绕流验算。

6 结论

提出了修正主应力旋转理论，解决了原有主应力旋转理论不满足水平方向静力平衡的问题，采用主应力迹线方法求解时，对迹线上的点全部作极限状态假设，将导致被动状态下结果稍偏大，主动状态下结果稍偏小。将主应力迹线方法应用于抗滑桩桩间土绕流计算，揭示了桩的荷载分担比与土体性质、桩间净距的关系：c、φ值越小，桩的荷载分担比越小；L越大，桩的荷载分担比越小。定义了极限荷载下桩的荷载分担比与实际荷载下桩的荷载分担比之比为桩间土稳定性系数，可用于抗滑桩工程安全性的监测预警，也可在积累一定的工程监测数据后用于桩间土绕流验算以及基于桩间土稳定的桩距的确定。主应力迹线法研究还有待进一步深化，主应力迹线形状、迹线上土体真实应力状态还需进一步研究。若将本文成果扩展至三维空间，可为滑坡推力非线性分布计算提供理论依据。