装备保障备件需求预测算法*
2020-09-07康警予陈忠刘延杰蔡骏王晖
康警予,陈忠,刘延杰,蔡骏,王晖
(1.陆军装甲兵学院 演训中心,北京 100072;2.中国电子科技集团公司 第二十八研究所,江苏 南京 210007)
0 引言
随着我国综合国力的提高以及海外利益的扩展,为了维护正常的国际政治、经济秩序和国家利益,我国必将加强在国际事务中的影响力,强化维和任务的投入。鉴于维和地域形势需求及环境条件,维和任务量大、地域广、装备使用强度高,任务区域大多经济落后、交通基础差和资源匮乏。经济落后造成执行任务时所需施工材料就地供应困难,路网条件及交通基础设施差造成巡逻和运输困难,资源匮乏使物资就地采购补给困难,这些都给执行维和任务及维修保障带来极大困难。为了顺利执行维和任务,使维和装备处于良好的工作状态,必须有充足的维和装备保障配件。装备保障配件预测在境外作战条件下显得更加关键。
在需求预测方面,早期算法主要是层次分析法、回归算法等,由于是线性类算法,精度不高[1-2]。文献[3-5]已经将神经网络相关方法与装备保障预测进行结合起来,提出了一些有意义的想法,但这些算法运行时间长、容易陷入局部最优化,且在建模方面并没有将境外相关重要影响因素考虑进去。粒子群优化算法(particle swarm optimization,PSO)是基于群体智能的一种优化方法,能够解决局部最优的问题,已经得到广泛应用[6-7]。本文提出一种将PSO与BP(back propagation)神经网络相结合的PSO-BP神经网络算法(PSO-based BP neural network,PSO-BP),能够解决目前算法中存在的相关问题,同时,将境外作业相关定性因素进行量化建模分析,综合解决境外装备保障备件需求预测难题。
1 维和装备保障需求预测依据
组织实施任何维和装备保障,首先要明确保障任务、保障场景、保障目标、保障模式、保障内容、保障数量、保障时间、保障空间等问题,才能进行需求预测。本文深入探讨并准确回答这一问题,有利于深化、细化影响和制约维和装备保障需求的各种具体因素,为后续数据化维和装备类型、装备数量、装备输送、保障力量部署提供可靠的输入。
1.1 维和任务
没有维和任务就没有维和装备保障需求。因此,维和任务是维和装备需求预测的基础依据。
(1) 维和任务类型
面对不同的维和任务类型,维和装备保障会面临不同的需求。执行基建维和任务需要更多的工程装备和技术人员,执行人道救援维和任务需要更多的食品医疗物资与医疗人员,执行打击恐怖袭击的维稳任务需要更多的武器装备与作战人员。为使维和装备保障与维和任务保持同步,对维和装备、人员、指挥机构提出不同的要求。
(2) 维和任务编成
维和任务编成,根据任务需要,从各个部队中选取相应人员与装备,进行训练。投入任务的力量规模与科技含量,即投入人员多少与技能水平、装备的多少与技术含量。如果人员技能水平高,装备技术含量高、功能强大,投入维和任务的人员、装备数量不多,也可以较好地完成维和任务。
(3) 维和任务环境
维和任务环境是指维和行动的空间,包括社会(人文)环境和自然环境。社会环境一般包括政治环境、经济水平、社会发展、宗教信仰等;自然环境包括地理、气候、物产等信息。一般来说,自然环境对维和装备保障需求的影响更大些,当然社会环境,尤其是交通状况、社会稳定对维和装备保障需求的影响也极为重要。一般情况下,在其他条件相似的情况下,维和装备在自然环境好的地方比高温、高湿等地方故障率、损坏率更低,在交通便捷的地区比交通差的地区支援保障更加快捷。
1.2 保障构想
维和装备保障构想对维和装备保障需求的影响相对小一些,但对维和保障人员、维和装备、物资等的关系比较大。维和装备保障构想主要受到不同维和人员和不同行动方式等条件的制约。维和部队各种行动的实施与实现所采取的对策、措施、方式等也是不同的。部队在不同行动、不同阶段、不同时节,其维和装备保障方式亦不同,动用或所依赖的维和装备也不一样,进而对维和保障人员素质的要求也有区别。就是说,有什么样的维和任务,就有什么样的维和保障方式;有什么样的维和保障方式,就需要特定的维和装备、维和保障人员及维和保障指挥机构。
2 维和装备保障需求预测步骤
维和装备保障需求预测步骤如图1所示。
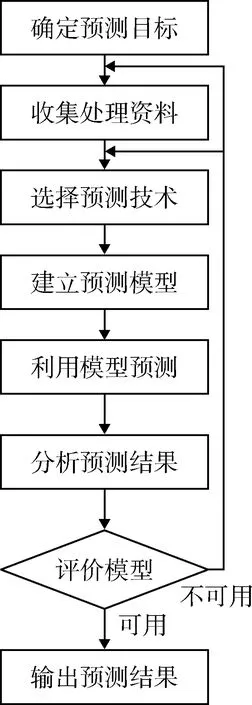
图1 预测基本步骤Fig.1 Basic forecast steps
(1) 确定预测维和装备保障需求目标
维和装备保障需求预测是为了完成维和任务,所以要根据维和任务的要求去确定预测的目标,如:工程设备备件、医疗设备备件、武器弹药等。根据维和装备保障需求发展的趋势,通过BP神经网络等技术,预测出相应装备备件需求量的变化。因此,当对维和装备保障需求的发展变化进行预测时,首先要了解维和任务需求,进行预测。
(2) 收集、处理资料
根据维和装备保障备件预测的问题要求,采集、处理各类所需的资料、数据,特别是维和装备保障需求的历史资料,以及各种影响预测的因素。
(3) 选择维和装备保障需求预测技术
需求预测技术的种类很多,如Bayesian法、Croston法、加权需求率模型、加权回归预测模型、加权移动平均法等。但由于各方面条件的限制,根据准确、经济、高效、方便的原则,满足混合多变量(同时存在多个定量和定性参数)需求预测,合理地选择预测技术,如通过粒子群优化算法,将多变量简化为单个子问题,实现高效精确的预测;通过one-hot encoding,dummy enconding或者factorize都可以将定性特征转化为定量特征,进行维和装备保障备件预测。
(4) 建立维和装备保障需求预测模型
维和装备保障备件需求预测模型可以对保障需求发展规律进行近似模拟。当搜集充足的历史数据后,采用相应技术处理,构建预测模型,描绘备件需求发展规律。
(5) 利用维和装备保障需求预测模型开展需求预测
根据当前的需求数据和预测模型,计算未来的保障需求。这种计算是建立在已有的规律上,而且在短时间内的发展规律不会发生大的变化。
(6) 分析预测结果、评价模型
维和装备保障需求预测模型反映的是保障需求发展规律。利用维和装备保障需求预测模型进行预测,得到的预测结果与实际结果并不是完全相符。因为预测模型只是近似模拟,不同预测模型之间存在差异,再选取表现较好的模型。通过分析实际与预测情况之间的差异,评价预测模型。
3 维和装备保障预测模型
维和装备保障预测结果的准确性,不仅与历史资料数据有关,而且预测模型也发挥着至关重要的作用。因历史数据少,维和装备保障预测是一种小样本条件下的预测,预测模型对预测结果的作用尤为凸显。因此,需要采用BP神经网络对小样本数据进行训练,粒子群优化算法简化学习代价。
BP神经网络具有结构简单、非线性映射能力强、自学习能力好等优点[8-11]。其采用梯度下降算法,使用训练数据进行学习,从而实现误差平方最小化[12],但是在BP神经网络结构复杂的情况下,则会遇到运行时间长,陷入局部最优等问题[13-14]。
粒子群优化算法(PSO)是基于群体智能的方法开展模型训练,能够解决局部最优的问题。因此,本文提出一种将PSO与BP神经网络相结合的PSO-BP神经网络算法,可以较快地完成学习。具体流程:首先,根据维和装备保障特点,选取特征变量;然后,将数据中选取的特征变量进行处理;最后,通过粒子群优化算法处理BP神经网络中的连接权值和阈值,不断迭代,获取最优解,从而建立PSO-BP神经网络算法模型。通过PSO-BP神经网络构建维和装备保障预测模型,与其他传统的方法相比,能够较好地避免局部最优问题,可以在更短时间内获取更准确的预测结果。
3.1 变量选择
维和任务远离本土,装备故障频发,装备种类庞杂,环境复杂,影响维和装备备件需求预测的因素较多,而且有些因素无法采用定量分析,只能进行定性描述,需要采用相应方法对定性描述变量转化为定量值。
为了全面反应装备保障需求的重要影响因素,本文选取任务类型、人员数目、装备种类、政治、经济、文化、气候、保障构想等18个相关变量构建PSO-BP模型(表1)。由表1可以看出,18个变量分为维和任务、人员投入、装备情况、社会因素、自然因素和保障构想6个维度,全面、综合地描述维和装备保障的各种影响因素,以满足维和装备保障需求预测。

表1 模型变量Table 1 Model variables
维和任务分为任务类型和担任角色,任务类型不同对备件需求也会存在差异,比如基础设施建设需要更多的工程设备,人道主义救援则需要食品医疗物资。而维和任务有些需要多国联合组织,每个国家在维和任务中担任不同的角色,若需要担任主要角色,则需要更完备的保障。
人员投入也会影响到备件需求,不同的人员数目,则会有不同的物资保障需求。人员的技能水平也会影响设备保障情况,技能水平越高,相关工程设备完成相同的任务,损耗越小,需要的备件越少。
装备情况对备件预测影响极大,主要从装备种类、装备数目和技术含量进行分析。武器弹药类的装备属于一次性的,而工程设施装备则可以重复利用。装备数量越多,技术含量越高,可以高效率地完成维和任务,则会减少备件消耗。
社会因素是执行维和任务需要考虑的情况。稳定的政治、良好的经济、繁荣的文化可以促进维和任务的完成,避免备件的损耗。完善的工业基础使部分备件可以就地获取,减少备件需求。高水平的人口素质可以得到当地的人员支持,减少维和人员配置。同时,发达的交通减少装备损耗,降低备件需求。
自然因素可以从地形、气候、资源方面进行分析。复杂的地形、恶劣的气候不仅会造成执行任务困难,还会加剧装备磨损,需要更多的备件保障需求。而贫瘠的资源无法就地获取材料进行补给,使备件保障需求增加。
保障构想则是对最终保障效果的期望,当期望越高时,则需要更多的备件才能完成高要求的维和任务。
3.2 数据来源及处理
本文研究数据来自维和任务的采集数据和不同地区的调查结果,数据采集为近几次的维和任务。由于表1中存在一些定性指标,表2将表1中一些定性指标,通过定性描述,将其转化为定量值。即表2中变量名称与表1中定性指标的变量名称相对应,并根据任务类型,进行定性描述与详细描述,给出相应的定量值。
不同的因子变量,其参数的值域不同。此外,有些参数值越大,维和装备保障压力越大;有些参数值越小,维和装备保障压力越大。由于本文中所使用的激活函数为Sigmoid函数(值域为[0,1]),因此,需要对数据进行归一化处理,将各参数映射到[0,1]的范围内,从而保证值越大,维和装备保障需求越大。
Sigmoid函数有单极性Sigmoid函数和双极性Sigmoid函数2种,单极性Sigmoid函数为
(1)
双极性Sigmoid函数为
(2)
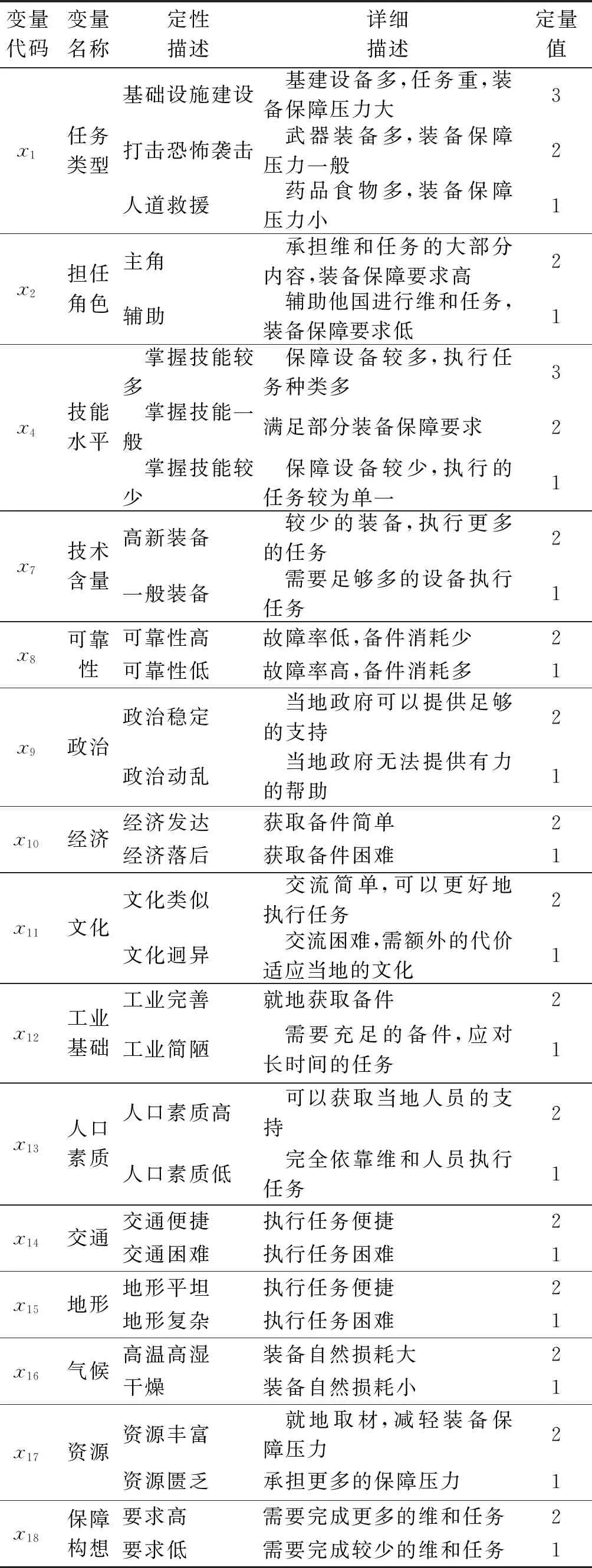
表2 各类定性参数的定量处理Table 2 Quantitative treatment of various qualitative parameters
式中:x为相应输入参数。采用最大最小变换法对不同参数进行归一化处理[15]。对于值越大保障压力越大的指标(x1,x2,x3,x5,x6,x18)采用式(3)进行归一化:
(3)
对于值越大保障压力越小的指标(x4,x7,x8,x9,x10,x11,x12,x13,x14,x15,x16,x17)采用式(4)进行归一化:
(4)
式中:y为归一化处理后的数值;x为某一参数的原始值;xmax为该参数所有可能值中的最大值;xmin为最小值。
3.3 粒子群优化算法
在本文中,定义,由n个粒子构成的d维空间用种群x=(x1,x2,…,xn)来表示,粒子i的速度表示为vi=(vi1,vi2,…,vid)T,位置表示为xi=(xi1,xi2,…,xid)T,其中i=1,2,…,n;粒子i到当前迭代为止搜索的最优位置记作pi=(pi1,pi2,…,pid)T。基于前面的最优位置,粒子i的状态可以通过下式更新:
vid(t+1)=w(t)vid(t)+c1r1(pid-xid(t))+
c2r2(pid-xid(t)),
(5)
xid(t+1)=xid(t)+vid(t+1),
(6)
(7)
(8)
式中:w(t)为惯性权重因子;c1和c2为加速常数;t为迭代次数;Tmax为最大迭代次数。
粒子i的速度在d维的速度为vid,超出边界值[-vmax,vmax],则会被限定在最大速度,其中正负为方向。当vid速度大于vmax,|vid|≥vmax分为2种情况,即方向为正vid≥vmax,则vid=vmax;方向为负vid≤-vmax,则vid=-vmax。vid速度小于vmax,则在限定范围内|vid| 基于PSO-BP神经网络模型构建过程如图2所示。 图2 基于PSO-BP神经网络模型建立流程图Fig.2 Flow chart based on PSO-BP neural network model 首先,确定BP网络结构,初始化粒子在总体的速度和位置,对输入数据进行归一化处理,并初始化神经网络的权重,训练网络并将误差作为粒子的适应度,选择个体最优位置作为全局最优位置。根据式(1),(2)计算粒子的位置和速度,然后计算每个粒子的适应度,以及每个粒子的最好位置pbest所对应的适应度,选择适应度最小的粒子位置作为pbest,比较每个粒子的适应度与种群所经历过最好位置的适应度,选择适应度更小的作为gbest,检查是否达到全局最优位置或达到最大迭代次数;若未达到预设条件,则继续更新,重新调整粒子速度和位置;如果能够达到前面设置的条件,则停止更新,输出相应的值作为BP神经网络初始值,再完成整个网络的训练和数据预测。 在整个流程中,持续迭代计算粒子群的速度和位置,获得与最优解接近的值,建立相应的神经网络。定义粒子适应度值为 (9) 式中:yi为样本i的观测值;ti为样本i的预测值;N为样本数量;abs为取绝对值函数。 通过本文提出的粒子群优化算法,不断更新迭代,在前后误差低于一定水平或者运行次数到达一定次数后,可认为得到系统所需的最优连接权值和阈值,建立神经网络模型。 本实验主要从维和任务、人员投入、装备情况、社会因素、自然因素、保障构想6个维度考虑,通过对应的18个变量进行分析。其中,任务类型x1、担任角色x2、技能水平x4、技术含量x7、可靠性x8、政治x9、经济x10、文化x11、工业基础x12、人口素质x13、交通x14、地形x15、气候x16、资源x17和保障构想x18为定性变量,可根据表2中的定量处理,取值满足表2的约束即可。人员数目x3、装备种类x5、装备数目x6为定量变量,取值应为正整数。已执行维和任务中备件消耗量如表3所示。 表3 PSO-BP模型训练数据集Table 3 PSO-BP model training data set 将表3中的变量参数作为输入变量,备件作为输出变量,引入到PSO-BP神经网络模型,运用Matlab神经网络工具箱中的newff命令对网络进行训练,学习速率取0.1,通过编程计算出网络输出,即可得预测值,如表4所示。 表4 PSO-BP模型预测结果 通过表4可以发现,通过PSO-BP模型,根据历史数据预测维和装备保障备件需求,预测结果与实际值接近,该预测模型具有较好的表现。同时结合表3,维和装备保障备件需求与任务类型、担任角色、设备可靠性,以及当地的工业基础联系较为密切。若负责基础设施建设对工程设施备件消耗更多,负责反恐则需要更多的武器弹药。担任角色极为重要,因为主导地位不同,负责的任务多少也存在差异。与此同时,设备越可靠,完成相同的任务,需求的备件越少,可靠性就地保障对需求预测也有很大影响。当地工业基础也是一个重要参考因素,若工业基础完善,很多备件可以及时获得,无需事先准备大量备件库存。 本文根据维和任务的具体情况,确定维和任务、人员投入、装备情况、社会因素、自然因素和保障构想中18个相关因子作为预测参数,基于PSO-BP神经网络建立了维和装备保障预测模型,运用Matlab软件,研究了预测原型系统。仿真表明,预测模型能够较好地分析维和装备保障相关因素的数据,较为准确地预测装备保障备件需求。随着维和任务的不断执行,在获取更多的数据后,持续优化本文算法,能够进一步提高预测性能。3.4 PSO-BP模型构建过程

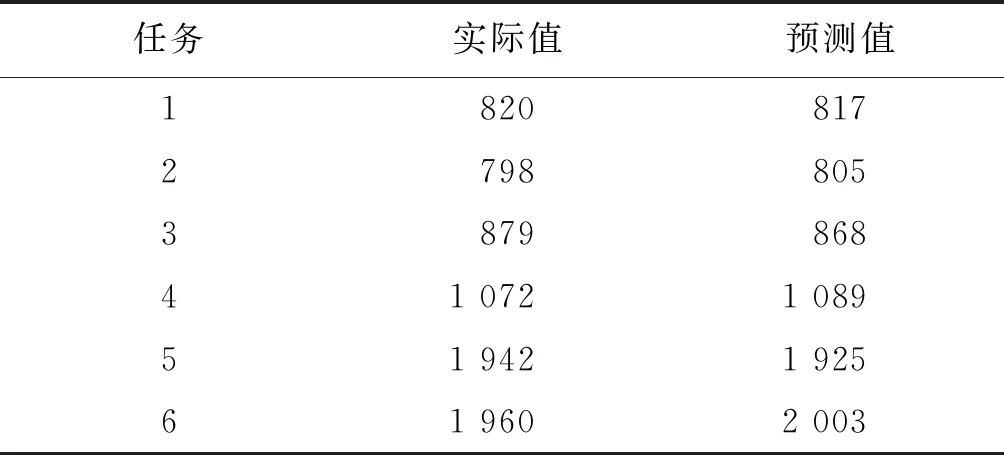
3.5 模型验证

4 结束语
