基于最小全变差的雷达测距方法*

杨明远，徐笛，江利中，丁红晖，顾泽凌，张衡

(上海无线电设备研究所，上海 200090)

0 引言

距离测量是雷达的基本任务之一[1-3]。基本上所有雷达都具备距离测量的功能，因此测距是雷达重要的功能。根据雷达发射信号的不同，雷达测距通常采用脉冲法测距、频率法测距和相位法测距。噪声是雷达测量精度的最主要限制[4]，无论哪种测距方法，由于噪声的影响很难确定波束中心的位置，从而影响波束中心距离估计精度。全变差正则化[5-7]通过引入一定的约束将数据降噪转化为适定问题，并能够确保数据原结果的存在性、唯一性，且具有噪声干扰较小的优点。本文利用最小全变差测距的方法可以有效地抑制噪声，提高数据的信噪比，进而提高波束中心距离测量精度。该测距方法可以应用于合成孔径雷达(synthetic aperture radar，SAR)回波的雷达成像中心距离估计。

1 波束中心距离测量原理

雷达波束中心的距离即雷达照射区域波束中心相对雷达平台的距离。雷达波束中心距离的估计原理是雷达平台在运动的过程中需要对照射区域进行照射，通过反射回来的回波信号形成和路回波和俯仰差路回波信号。通过俯仰差通道数据比上和路数据来测量每个距离门偏离波束中心方向的俯仰角度,并得到波束中心的距离。而实际过程中雷达回波中掺杂有噪声，差比和数据受到噪声的影响很难找到零点的位置，从而造成距离测量不准确。因此通过对差比和数据进行全变差降噪，改善差比和的数据的信噪比，降噪后的数据可以很容易找到差比和数据的零点。最后寻找俯仰角度等于0所对应的距离门即为波束中心的距离。图1为建立的波束中心距离测量的几何模型。

图1 波束中心距离测量的几何模型Fig.1 Geometric model of beam center ranging

根据上面的描述，给出全变差降噪的波束中心距离估计方法的流程，如图2所示。

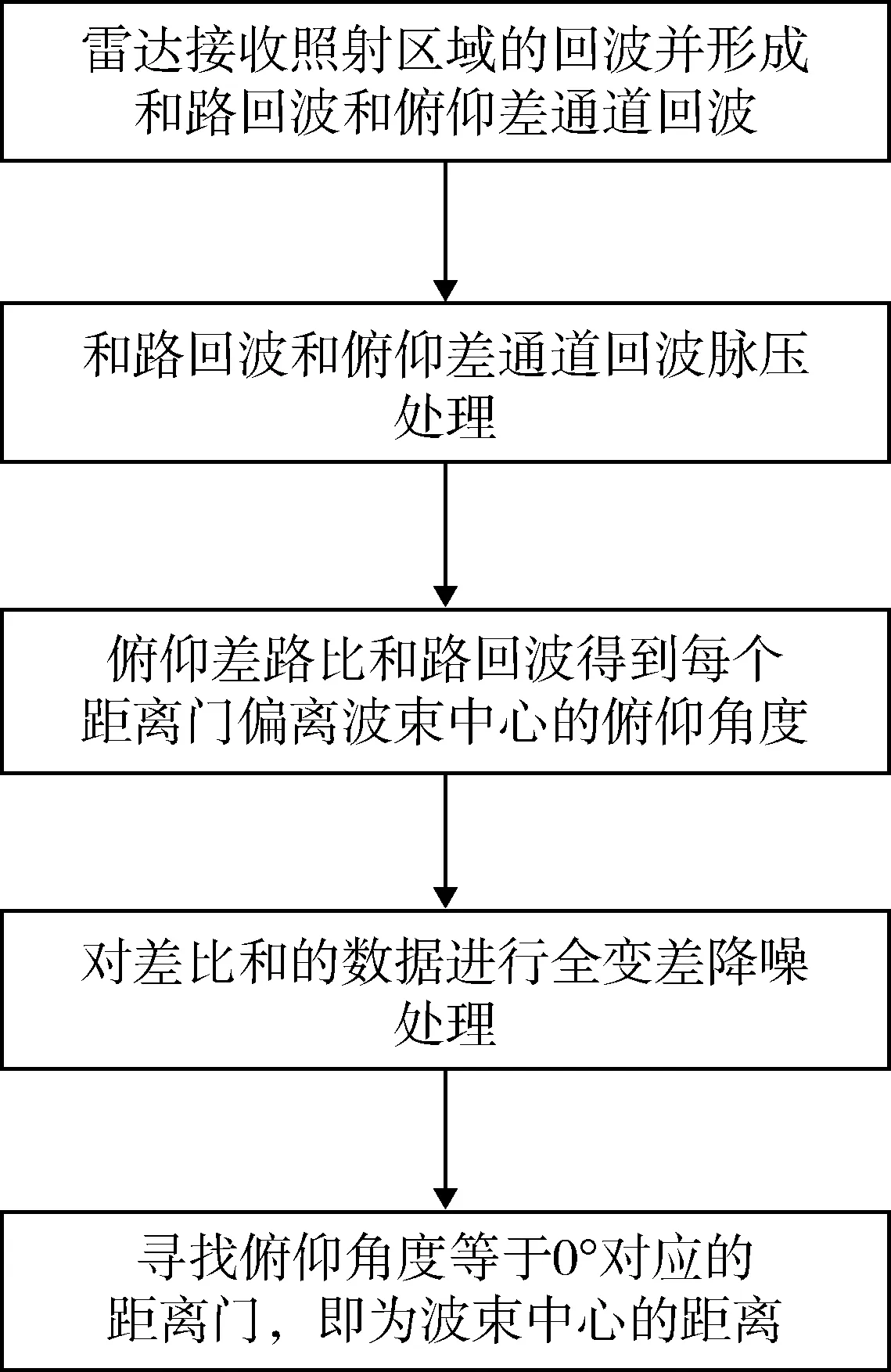
图2 全变差降噪的波束中心距离估计流程图Fig.2 Flow chart of beam center distance estimation based on total variation noise

2 波束中心测距方法

2.1 俯仰和差回波测角

波束中心距离估计方法中需要估计俯仰向每个距离波门偏离波束中心的俯仰角度。然后找到俯仰角度为0°所对应的距离门即为波束中心的斜距[8]。这种波束中心距离估计方法需要雷达天线具有和差器，可以形成和通道回波数据和俯仰差通道回波数据，并能够接收和通道回波信号和俯仰差通道回波信号。此外，该波束中心距离估计方法要求雷达能够处理俯仰和差通道的回波信号，进而得到每一个距离门的俯仰向角度。图3给出了俯仰和差角度估计示意图，俯仰角度可由图中的简单的几何关系可以得到：

(1)

式中：H为平台高度；Rref为波束中心的斜距；βref为波束中心的擦地角；Rn和βn为第n个距离门下的斜距和擦地角；俯仰角度θn为第n个距离门与波束中心的俯仰方向夹角。

从式(1)得出俯仰角度θn与距离门对应的斜距Rn关系，波束中心的距离对应的俯仰角度θn为0°。因此通过俯仰和差回波测角得到距离门偏离测波束中心的俯仰向角度，测得偏离俯仰角度为0°即为所要估计的角度值。

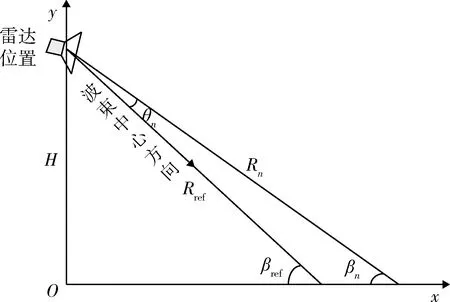
图3 俯仰和差角度估计示意图Fig.3 Vertical sum-difference angle estimation diagram

俯仰和差通道回波测角方法有比幅测角和比相测角2种方法[9]，本文以比幅测角进行处理。由于回波数据中噪声的能量比较强，数据受到噪声的影响，无法直接利用回波数据和差比幅进行角度估计，需进行距离脉压处理。将距离脉压后的回波数据再通过差比和的比幅法进行俯仰角度估计，这样就可以得到距离向各个距离偏离波束中心的俯仰角度θn。由比幅测角的基本公式：

(2)

式中：sn和dn分别为距离脉压后第n个距离门的和差通道回波信号；K为差斜率；Im()表示取复信号的虚部，取虚部还是实部根据测角系统而定。

2.2 和差通道测距误差

由上分析可知，和差比幅测距的基本原理是，对雷达回波的每个距离门的差通道信号与和通道信号作比值后，寻找零深对应的距离门，并将该距离门对应的距离作为波束中心对应的距离。

假定雷达天线俯仰上2个子通道的信号分别为a1和a2，则差通道的信号dn为俯仰上2个子通道的差值：

dn=a1-a2，

(3)

和通道信号sn为俯仰上2个子通道的和

sn=a1+a2,

(4)

差通道与和通道信号的比值为

(5)

在波束中心附近，由式(2)得差通道与和通道信号比值sd/s与距离门偏离波束中心的角度θn的关系可以表示为

sd/s=Kθn.

(6)

根据几何关系，距离门偏离波束中心的角度θn与斜距Rn的关系为

(7)

由式(3)～(7)可以联立得到

(8)

斜距Rn分别对a1和a2求偏导，得到

(9)

(10)

假定噪声导致的a1和a2的误差都为εs，则和差通道测距误差为[10]

(11)

波束中心为0的方向俯仰上2个通道的差为0，即

a1-a2=0.

(12)

因此式(11)变为

(13)

εs为噪声误差，因此式(13)中εs/(a1+a2)即与信噪比相关，因此通过理论分析可知，噪声水平决定测距精度的高低。通过全变差对和差比幅数据进行降噪处理减小噪声误差值，可以有效提高信噪比，提高测距精度。

2.2 全变差降噪测距

由于回波数据中噪声的能量比较强，和差比幅数据受到噪声的影响，无法直接通过寻找俯仰角度等于0°对应的波束中心距离。全变差对应的物理意义就是输入信号的平滑度。为了消除噪声对测距的影响，需要将和差比幅数据变得平滑，也就是对和差比幅数据进行去噪处理。一种很直观的想法就是让数据的全变差变小[11-12]。通过对全变差定义分析可以发现，全变差可以描述波形的平坦度，并且波形越平坦，全变差越小。设原始无噪声回波数据进行和差比幅结果为U，Un为被噪声污染的回波数据得到的和差比幅结果，即：

Un=U+N,

(14)

式中：N为具有零均值，方差为σ2的高斯白噪声。

将总变差定义为梯度幅值的积分[13]得到

(15)

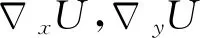
(16)

一般梯度下降流是解梯度p次方的泛函的最小值，其中：

(17)

为了计算梯度下降流引出欧拉-拉格朗日方程[14]

(18)

令

(19)

由式(18)得：

(20)

当p=1时，得到全变差模型的梯度下降流：

(21)

根据全变分的原理可知限制总变差就会限制噪声，因此可以将数据降噪问题转换为最小化问题。为了使降噪后的数据与原始数据的差距不会特别大(数据不失真)，在求解梯度极小值时增加一个保真项，将数据的降噪问题转换成如下的最小化问题：

(22)

式中：λ|U-Un|为保真项；λ为正则化参数，调整保真项与梯度的占比。

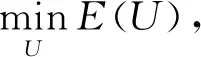
E(U)=J(U)+λ|U-Un|.

(23)

通过上面分析下面给出全变差的求解过程，由式(23)得到离散全变差迭代式(24)，图4为全变差迭代流程图。J(U)的离散迭代公式[15]

(24)

式中：m=1,2，…，M为迭代次数；i=0,1,…，I；j=0,1,…，J分别为和差比幅数据的距离向和方位向点数；Δt为迭代步进。

3 仿真分析

3.1 理论仿真

波束中心距离估计方法中需要估计俯仰向每个距离波门偏离波束中心的俯仰角度；然后找到俯仰角度为0°所对应的距离门即为波束中心的斜距。因此，俯仰角度的估计精度决定波束中心距离的测量精度。下面通过仿真分析俯仰角的测量精度。实验仿真参数设置：子阵个数为80，其中方位向阵元个数为10，俯仰向阵元个数为8；阵元间距为半波长，给出波束指向0°的天线方向图。图5为雷达天线方向图，红色为和波束天线方向图。

图4 全变差降噪流程Fig.4 Total variation noise reduction process

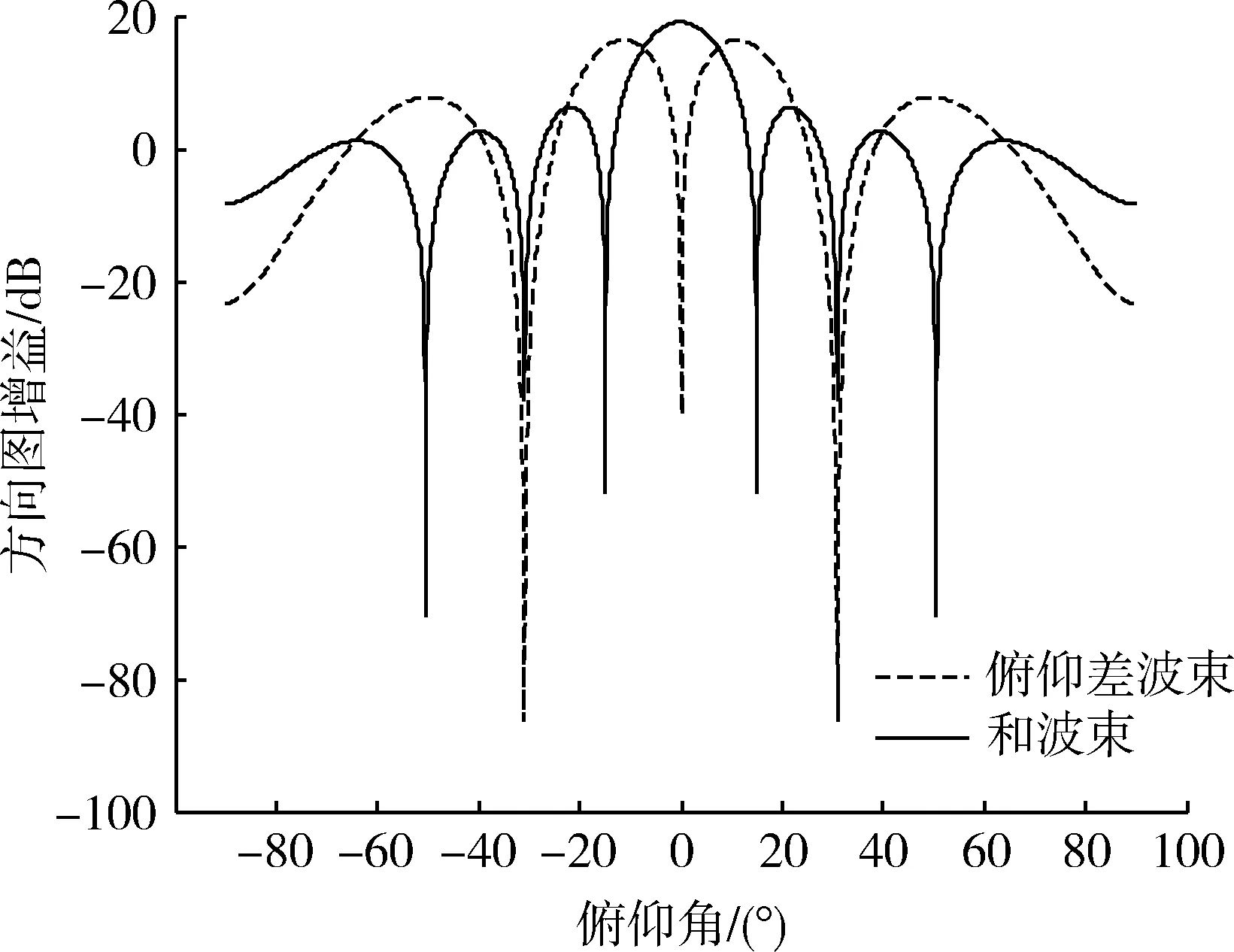
图5 天线方向图Fig.5 Antenna pattern

由俯仰差比和得到单脉冲比值，在回波中加入高斯白噪声使得信噪比为20 dB，得到如图6所示的单脉冲比值，由于噪声的影响单脉冲比值在真实单脉冲比值附近进行波动，因此若不对单脉冲比值进行有效的处理很难估计到俯仰角为0°对应的距离。

图6 加噪声后单脉冲比值仿真结果Fig.6 Simulation results of monopulse ratio after adding noise

采用基于最大熵准则对单脉冲比值进行估计。图7为最大熵准则处理后的单脉冲比值结果。从图7的仿真结果可以看出，由于噪声的影响，该方法估计性能并不理想。基于最大熵准则的方法对噪声的敏感性较强，不利于在有噪声条件下的角度估计。

图7 最大熵准则处理后的单脉冲比值仿真结果Fig.7 Simulation results of single pulse ratio after maximum entropy criterion processing

采用基于最小全变差的方法对单脉冲比值进行估计。图8为全变差滤波处理后的单脉冲比值结果。从图8的仿真结果可以看出，经过全变差滤波处理后的单脉冲比值与真实单脉冲比值非常接近，滤波效果很好。

图8 全变差滤波处理后的单脉冲比值仿真结果Fig.8 Simulation results of single pulse ratio after total variation

改进信噪比对滤波后的数据相对于原始数据的信噪比变化情况进行量化，可以直观地看出滤波后数据的改善程度，并且易实现。通过改进信噪比来衡量基于最大熵方法和最小全变差方法单脉冲比值滤波效果，改进信噪比公式为

(25)

从式(25)可以看出，改进信噪比越大，滤波效果越好。此外，解的相对误差也可以描述数据的滤波效果，解的相对误差为

(26)

从式(26)可以看出，解的相对误差越小，滤波效果越好。

由式(25)和式(26)分别计算最大熵准则和最小全变差方法估计后的单脉冲比值效果，表1为2种优化算法处理效果比较。

表1 2种优化算法处理效果比较Table 1 Comparison of processing effects of two optimization algorithms

从表1中计算数据可以看出，最小全变差处理后的单脉冲比值其解的相对误差较小，其改进信噪比较大。通过理论仿真分析可知，最小全变差方法对噪声抑制效果优于最大熵准则，因此针对高斯白噪声下的数据最小全变差方法能够取得很好的滤波效果。

图9为全变差滤波前后的测角精度仿真结果，从图中可以看出测角误差与信噪比成反比的关系，随着信噪比的增大测角误差逐渐减小。当信噪比比较低的时候，由于噪声的影响测角精度比较差，而通过全变差滤波处理后的测角精度得到大大改善。

图9 全变差滤波前后测角精度仿真结果Fig.9 Simulation results of angle measurement accuracy before and after total variation

通过理论仿真分析可知，通过全变差对俯仰差路回波和和路回波进行滤波处理，可以有效抑制噪声，提高角度估计精度，进而得到高精度波束中心的距离。

3.2 实测数据仿真

下面通过实测数据进行仿真分析，实测过程中雷达平台的飞行速度是120 m/s，方位角为13°，信号带宽为30 MHz，采样率为40 MHz，脉冲宽度为20 μs，脉冲重复频率为2 kHz。实测数据中方位向总共有9 920个脉冲，这里以64个脉冲为一组进行波束中心距离测量，总共有155组数据。

图10为全变差降噪前的差比和结果，从图中可以看出实测数据中由于噪声的影响，和差比幅数据很难确定零深的位置。直接通过和差比幅数据进行波束中心距离估计很难，而且估计结果误差很大。

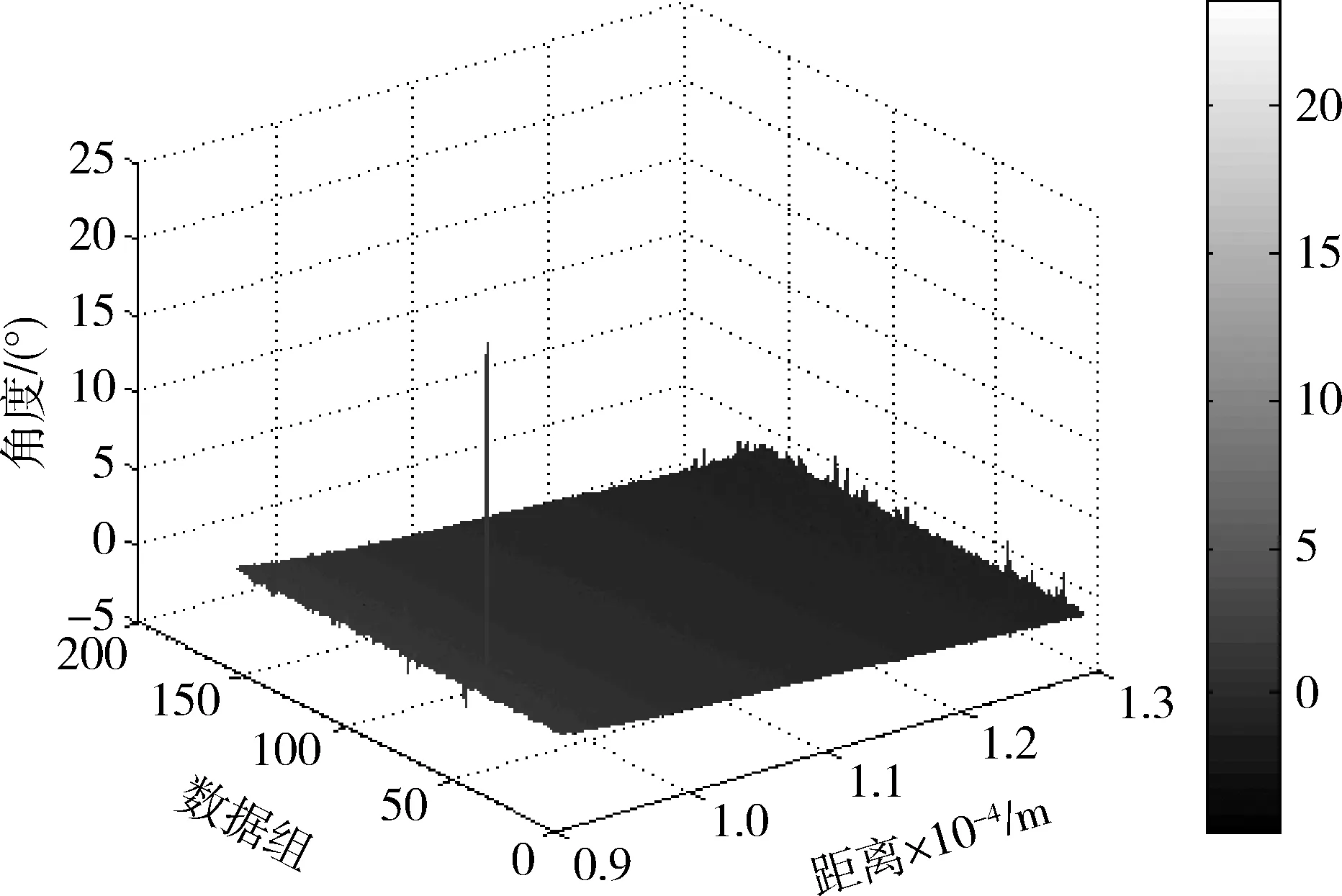
图10 全变差降噪前差比和结果Fig.10 Sum-difference’s results before total variation noise reduction

图11为全变差降噪后的差比和结果，从图中可以看出通过全变差降噪处理后，数据变得平滑，波形变得比较平坦，因此很容易得到差比和数据零深所对应距离门。通过全变差降噪处理后，数据信噪比得到提高，波束中心距离估计精度得到改善。

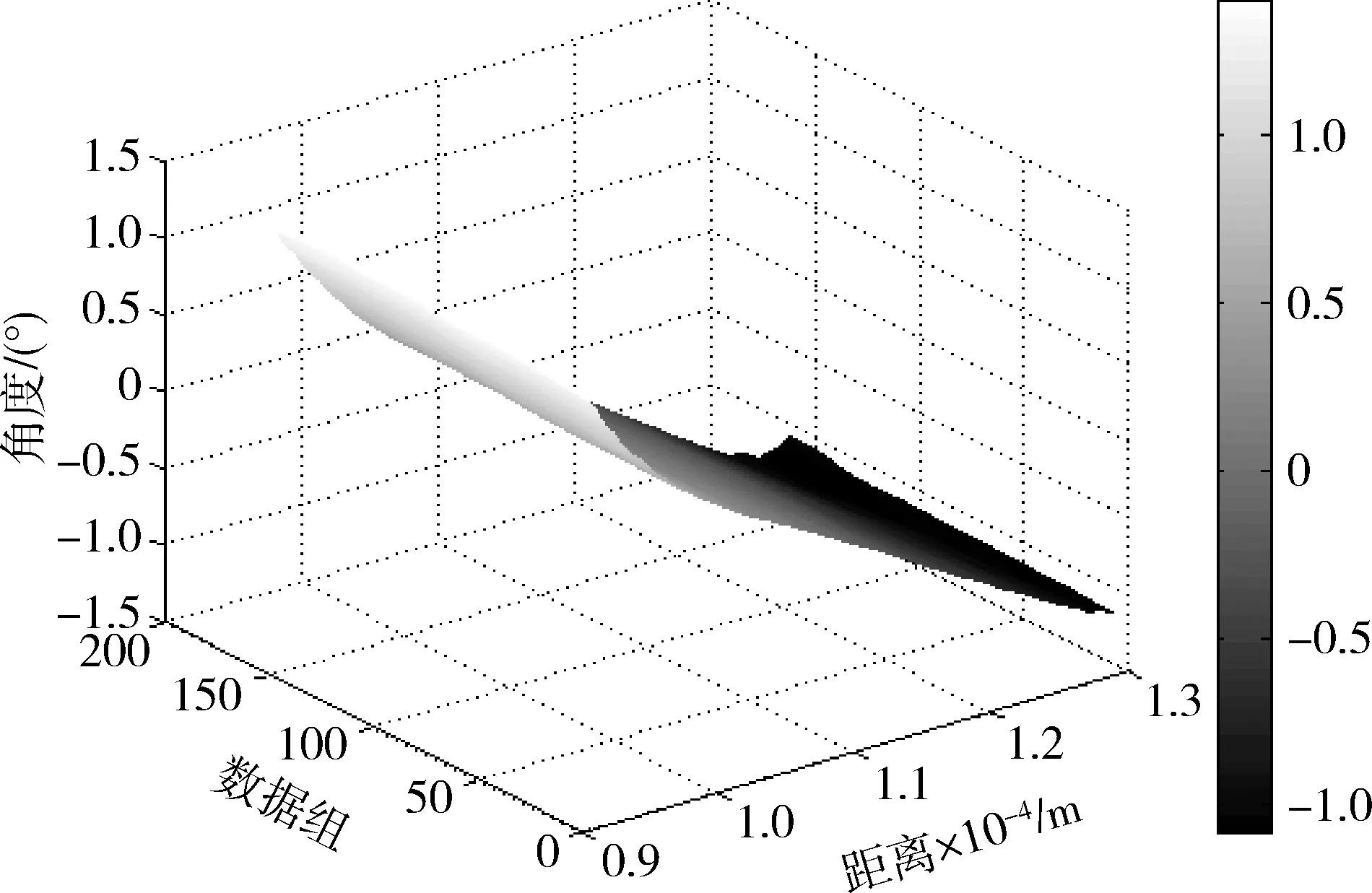
图11 全变差降噪后差比和结果Fig.11 Sum-difference’s results after total variation noise reduction

取其中一组数据进行观察，如图12所示，为一组全变差降噪前后的差比和结果，从处理结果可以看到通过降噪处理，数据变得平坦，而且零深的位置比较容易确定。

图13为全变差降噪前后距离估计结果，其中降噪前的距离估计结果由于噪声的影响波动较大；而降噪后的距离估计结果波动很小，距离估计精度相对较高。计算最小全变差处理前的波束中心距离估计的标准差为49.5 m，最小全变差处理后的波束中心距离估计的标准差为4.7 m。通过降噪前后的测距误差计算结果可知，通过全变差降噪后得到的距离估计精度较高。

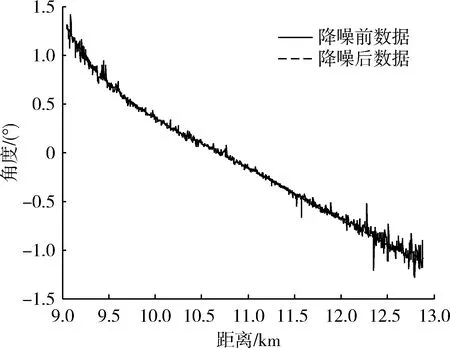
图12 一组全变差降噪前后差比和结果Fig.12 A set of sum-difference’s results before and after total variation noise reduction

图13 全变差降噪前后距离估计结果Fig.13 Distance estimation result before and after total variation noise reduction

通过实测数据仿真分析可知，基于最小全变差的波束中心距离估计方法能够有效改善数据的信噪比，提高距离的估计精度。

4 结束语

本文提出了基于最小全变差的雷达高精度距离测量方法，分析了波束中心距离估计误差主要由噪声影响，另外由于噪声越强全变差越大，因此通过最小全变差的方法有效降低噪声水平。同时通过理论仿真比较了最大熵准则与最小全变差2种方法在单脉冲比值估计能力，由于最大熵的方法易受噪声影响，单脉冲比值估计效果比较差；而最小全变差方法具有很好的噪声抑制能力，该测距方法通过对数据的全变差正则化处理，有效改善了差比和数据的信噪比，使得处理后的单脉冲比值数据变得相对平坦，从而能够很容易地找到差比和零深所对应的距离门。最后通过实测数据仿真分析可知，全变差降噪处理后的距离估计值精度较高，可以应用于雷达距离测量。